Determinação do módulo de Young em sólidos a partir da medida da velocidade do som pelo método do tempo de voo

Determining the Young's modulus on solids from the measurement of the speed of sound by the time-of-flight method

Resumos

O módulo de Young ($Y)$ é uma grandeza relacionada à elasticidade linear de um material. As técnicas mais comuns para se determinar o módulo de Young envolvem a medida da deformação de uma barra quando flexionada, ou a medida da deformação de um fio quando submetido a um esforço de tração. Outra técnica conhecida consiste na medida da velocidade do som ($c)$ numa barra fina, a qual está relacionada a $Y$ pela expressão $Y=\rho c^2$, onde $\rho$ é a massa específica do material em estudo. Desse modo, conhecendo-se $\rho$, a determinação de $Y$ se resume a medir $c$. Neste trabalho lançamos mão do método do tempo de voo de um pulso de compressão produzido em experimentos de colisão para medir a velocidade do som em diferentes materiais. O tempo de voo é o tempo necessário para um pulso de compressão percorrer a distância entre dois pontos da barra. Esse tempo foi medido através de uma montagem que utiliza duas chaves de contato mecânico associadas a um circuito elétrico contendo um contador eletrônico e um oscilador a cristal. Os experimentos foram realizados utilizando-se diferentes materiais (aço inox, latão e madeira) e calculados os respectivos módulos de Young com seus desvios estatísticos.

Palavras-chave:
Módulo de Young; elasticidade; pulso de compressão; tempo de voo; contador digital

The Young's modulus $\left(Y\right)$ is a quantity related to the linear elasticity of a material. The most common techniques for determining the Young's modulus involve the measurement of the deformation of a flexed beam, or the measurement of the deformation of a wire submitted to a tractive effort. Another known technique consists of measuring the speed of sound $\left(c\right)$ on a thin rod, which is related to $Y$ by the expression $Y=\rho c^2$, where $\rho$ is the density of the material under study. Thus, by knowing $\rho$, $Y$ can be determined through the measurement of $c$. In this work we carried out collision experiments to generate compression pulses in thin solid rods and employ the time-of-flight method to measure the speed of sound in different materials. The flight time is the time needed for the pulse to cover the distance between two points of the rod. This time was measured by means of an assembly which utilizes two mechanical contact switches associated with an electric circuit comprising an electronic counter and a crystal oscillator. The experiments were conducted using different materials (stainless steel, brass and wood) and calculated the respective Young's modules and their statistical deviations.

Key words:
Young's modulus; elasticity; compression pulse; flight time; digital counter

1. Introdução

O conceito de corpo rígido é bastante útil quando iniciamos o estudo da mecânica; no entanto, não passa de mera abstração. Todo corpo real deforma-se, em maior ou menor grau, quando submetido à forças externas ou a torques. Se depois de deformado por uma força (ou torque) o corpo volta para sua forma original, dizemos que seu comportamento é elástico. Se a força ultrapassar um determinado valor (limite elástico) a deformação será irreversível. No regime elástico, uma rápida perturbação é transmitida sucessivamente de uma partícula para outra contigua com velocidade finita. Por isso a compressão produzida por uma pancada na extremidade de uma barra cilíndrica propaga-se ao longo da barra com uma velocidade bem definida, que depende do tipo de material que constitui a barra, mas não da intensidade da pancada [1].

A elasticidade de um material pode ser caracterizada por meio de constantes elásticas, tais como os módulos de Young, de torção ou de cisalhamento, que relacionam forças ou torques com as deformações correspondentes. Esses módulos, definidos independentemente das dimensões de uma amostra em particular, têm grande importância prática tanto do ponto de vista científico como técnico. Científico porque podem fornecer informações importantes sobre as forças internas que mantêm unidas as partículas de um corpo e técnico porque engenheiros precisam conhecer as propriedades elásticas dos materiais que vão utilizar em seus projetos [2–5]. Neste trabalho nos limitaremos apenas ao módulo de Young.

O módulo de Young, que basta para descrever problemas em que apenas uma dimensão é importante (extensão ou compressão de uma barra, por exemplo [2]), é definido como a razão entre a tensão aplicada (força por unidade de área) e a elongação resultante (variação relativa do comprimento de amostra). Nesta definição, assume-se que o comprimento do corpo é muito maior que suas dimensões laterais [6]. Métodos para determinar o módulo de Young $\left(Y\right)$, descritos em textos para laboratório de física básica [7–9], podem ser agrupados em duas categorias: métodos estáticos e métodos dinâmicos [4,6].

Num método estático, a amostra do material em estudo é submetida a uma tensão visando provocar uma deformação elástica mensurável [10]. Num dos experimentos clássicos, $Y$ é determinado diretamente a partir da definição estudando-se a variação do comprimento de um fio longo quando submetido a um esforço de tração [7,11]. Outra possibilidade é estudar o deslocamento vertical da extremidade livre de uma barra, inicialmente na horizontal e com a outra extremidade engastada num suporte fixo, em função da carga afixada na extremidade livre [8,9].

Numa medida dinâmica, o módulo de Young também pode ser determinado de várias maneiras. Numa delas, a determinação é feita a partir da freqüência natural de oscilação de uma haste que tem uma de suas extremidades presa e em cuja extremidade livre é fixada uma carga suficiente para provocar apenas uma pequena deformação [8,9]. Numa outra, pode também ser determinado a partir de uma das freqüências de ressonância de uma haste, com uma ou ambas as extremidades presas, forçada a vibrar lateralmente por meio de algum dispositivo eletromecânico [4,6,12].

Como discutiremos a seguir, outra técnica conhecida envolve a medida da velocidade do som ($\left(c\right)$ propagando-se ao longo de uma barra fina; conhecendo-se $c$ e a massa específica $\left(\rho \right)$ da barra, $Y$ pode ser calculado a partir da expressão $Y=\rho c^2$, que vale para sólidos elásticos em que apenas uma dimensão é relevante. A velocidade de propagação do som numa barra pode ser determinada tanto por procedimentos diretos como indiretos. Num procedimento direto, conhecido como método do tempo de voo [13–18], mede-se o tempo necessário para um pulso percorrer uma distância conhecida na barra. Nos métodos indiretos mais usuais, mede-se o comprimento $\left(\lambda \right)$ de uma onda sonora propagando-se na barra; conhecida a frequência $f$ do som, obtêm-se a velocidade de propagação por meio da equação $c=\lambda f$ [19–22].

O objetivo deste trabalho é justamente determinar $Y$ a partir da velocidade do som, propagando-se ao longo de uma barra fina do material em estudo, medida pelo método do tempo de voo. Para isso, montamos um arranjo que consiste essencialmente em duas chaves de contato mecânico separadas espacialmente ao longo da barra. Essas chaves são formadas por esferas de aço encostadas em suportes metálicos presos à barra, cujos contatos abrem-se durante um pequeno intervalo de tempo quando da passagem do pulso de compressão. Cada esfera está ligada eletricamente a um contador digital que permite a medida do intervalo de tempo (tempo de voo) que o pulso leva para percorrer uma distância conhecida ao longo da barra. O circuito projetado para acionar as chaves utiliza componentes eletrônicos simples e de baixo custo e sua operação e montagem são descritas em detalhes. No que segue, iniciamos com uma introdução teórica sobre o módulo de Young (item 2.1) e deduzimos sua relação com a velocidade do som em uma barra fina (item 2.2). Descrevemos então a montagem e o princípio de operação do arranjo mecânico (item 3.1). Os componentes do circuito eletrônico e seu funcionamento são descritos em seguida (itens 3.2 a 3.4). Finalmente, são apresentados os resultados experimentais obtidos para três diferentes materiais (aço inox, latão e madeira) e calculadas as grandezas de interesse com seus respectivos desvios estatísticos (item 4). Para concluir, são apresentadas as considerações finais (item 5), agradecimentos e referências bibliográficas.

2. Teoria

2.1. O módulo de Young – definição

Respeitado o limite elástico, uma alteração $\mathrm{\Delta }l$ no comprimento $l$ de um fio sob ação de uma força $F$ será, segundo a lei de Hooke [1,5], dada por

(1) $$\mathrm{\Delta }l=KF,$$

onde a constante $K$ é uma característica do corpo que sofreu a deformação. Mas, às vezes, é mais interessante trabalhar com uma constante que seja característica do material e não do corpo.

Imaginemos uma carga (peso) suspensa por um fio preso no teto. Por causa da carga suspensa, o fio estica-se, isto é, seu comprimento $l$ sofre um acréscimo. Se tomarmos um pedaço do mesmo tipo de fio, mas com comprimento $2l$, então sob a ação da mesma carga, o acréscimo no comprimento deste segundo fio será o dobro do primeiro, e assim por diante. Desse modo, desde que não se exceda o limite elástico do fio, isto é, desde que não haja deformação permanente, o acréscimo $\mathrm{\Delta }l$ no comprimento $l$ do fio para uma dada carga é proporcional ao comprimento do fio ($\mathrm{\Delta }l\propto l$). Se, por outro lado, a carga for suspensa por dois pedaços de fio idênticos, presos no teto um ao lado do outro, o acréscimo no comprimento de cada fio será a metade daquele sofrido por um único desses pedaços sujeito à mesma carga; isto também aconteceria se, em vez de dois fios idênticos, tivéssemos escolhido um fio do mesmo material, mas com o dobro da seção reta do fio originalmente usado. Assim, em geral, o acréscimo no comprimento para uma dada carga é inversamente proporcional à seção transversal $A$ do fio ($\mathrm{\Delta }l\propto A^{-1})$. Mas, pela Lei de Hooke, $\mathrm{\Delta }l$ também é proporcional à força $F$ exercida pela carga. Combinando os últimos resultados, concluímos que $\mathrm{\Delta }l\propto lF∕A$, isto é,

(2) $$\frac{\mathrm{\Delta }l}{l}=\kappa \frac{F}{A}$$

onde $\kappa$, denominado coeficiente de elasticidade, depende somente do material usado para confeccionar o fio. Entretanto, é mais conveniente, ou mais comum caracterizar o material por meio da grandeza inversa, $Y=1∕\kappa$, denominada módulo de Young. Combinando esta definição com a Eq. (2), obtemos então,

(3) $$Y=\frac{F∕A}{\mathrm{\Delta }l∕l}$$

que é a expressão para a Lei de Hooke em termos do módulo de Young [2]. A razão $F$/$A$, força por unidade de área da seção reta, é denominada tensão ($\sigma$) e a variação relativa do comprimento do fio $\mathrm{\Delta }l∕l$, é denominada elongação $\left(\epsilon \right)$. Com essas definições, a Eq. (3) se transforma em,

(4) $$Y=\sigma ∕\epsilon \text{ou}\sigma =Y\epsilon .$$

A Eq. (3) também pode ser escrita como,

(5) $$F=YA\frac{\mathrm{\Delta }l}{l}.$$

Da Eq. (4) concluímos também que, quando $\mathrm{\Delta }l=l$, temos $Y=\sigma$, ou seja, o módulo de Young $Y$ pode ser interpretado fisicamente como a tensão que se deve aplicar no fio para dobrar seu comprimento (se a experiência fosse possível).

2.2. Relação entre o módulo Young e a velocidade de propagação numa barra.

Considere, inicialmente, uma barra cilíndrica fina em repouso sobre uma superfície plana horizontal e com suas extremidades livres. Considere também que a barra é elástica, tem seção transversal de área $A$, massa específica $\rho$ e que não existe atrito entre ela e a superfície plana. Suponha, agora, que uma das extremidades da barra receba um impacto de curta duração (como a batida de um martelo, por exemplo). Se a barra fosse rígida, ela se poria em movimento como um todo devido ao impulso recebido. No entanto, devido à elasticidade do material, apenas uma porção da massa da barra participa inicialmente do movimento [1,2,23]. Para entender isso, analisemos o que acontece com a barra quando a força $F$ indicada na Fig. 1 atua numa de suas extremidades durante um intervalo de tempo dt suficientemente pequeno para que a força possa ser considerada constante. Como a barra é elástica, a ação da força provoca uma compressão e a extremidade da barra avança uma pequena distância $dx=udt$, onde $u$ é a velocidade de deslocamento dessa extremidade durante o intervalo $dt$. Mas durante esse mesmo tempo, a frente da perturbação (compressão) avança uma distância $\delta x_0=cdt$, onde $c$ é a velocidade de propagação do pulso produzido pela força $F$.

Figura 1
Deslocamento (compressão) elementar de uma das extremidades de uma barra fina devido à ação de uma força durante um intervalo de tempo infinitesimal.

Note que são duas velocidades distintas. Uma é a velocidade $c$ de propagação da perturbação que desejamos determinar. A outra é a velocidade $u$ da extremidade frontal da barra durante o impacto e também a velocidade associada ao deslocamento de um ponto da barra quando alcançado pela perturbação. Um ponto da barra na posição $x=\delta x_0$, por exemplo, só se deslocará ligeiramente da sua posição de equilíbrio quando, decorrido o tempo $dt$, a perturbação passar por essa posição. A variação da quantidade de movimento da fração $\delta x_0$ da barra que foi perturbada no intervalo $dt$ é, portanto,

(6) $$dp=udm,$$

onde $dm={\rho }_{1}A\left(c-u\right)dt=\rho Acdt$ representa a massa da região hachurada (Fig. 1b) e ${\rho }_1$ a massa específica dessa região. O impulso correspondente é, então, $Fdt=dp=\rho Acudt$ e

(7) $$F=\rho Acu.$$

(Observe que a força é proporcional à velocidade e não à aceleração das partículas. Isto ocorre porque, devido à elasticidade da barra, a massa que participa do movimento aumenta a uma taxa $dm∕dt=\rho Ac)$. Mas, pela Eq. (5),

(8) $$F=YA\frac{dx}{\delta x_0}=YA\frac{dx}{cdt}$$

De (7) e (8), resulta, portanto,

(9) $$Ydx=\rho c^{2}udt.$$

No entanto, $dx=udt$, logo

(10) $$Y=\rho c^2$$

É interessante observar que o movimento de compressão não cessa mesmo após o término do impacto. Devido ao impacto, a fração de comprimento $x_0=c\mathrm{\Delta }t$ da barra que participou do movimento sofreu um encurtamento $\mathrm{\Delta }x={\int }_0^{\mathrm{\Delta }t}udt$, onde $\mathrm{\Delta }t$ é a duração do impacto, como mostra a Fig. 2b.

Figura 2
Processo de compressão da barra: $a)$ imediatamente antes do impacto ($t$ = 0), $b)$ imediatamente após o término do impacto ($t=\mathrm{\Delta }t)$ e $c)$ após o término do impacto ($t>\mathrm{\Delta }t)$. A área hachurada corresponde à região comprimida da barra.

No instante $t=\mathrm{\Delta }t$, quando $F=0$, as partículas na face de trás da região comprimida voltam para sua posição de equilíbrio enquanto aquelas na face da frente ainda estão em movimento e portanto impulsionando as partículas à frente. Por essa razão, o pulso de compressão continua progredindo (Fig. 2c), atinge a extremidade direita da barra, retorna e volta novamente. Associado ao movimento de vai e vem do pulso existe também o movimento periódico da barra, cuja face avança e pára. Mas essa situação não perdura indefinidamente; quando todos os pontos da barra voltarem para sua posição de equilíbrio, o que pode acontecer em décimos de segundos, a barra passa a se movimentar como se fosse um corpo rígido [1,23,24].

3. Montagem experimental

3.1. Descrição da montagem

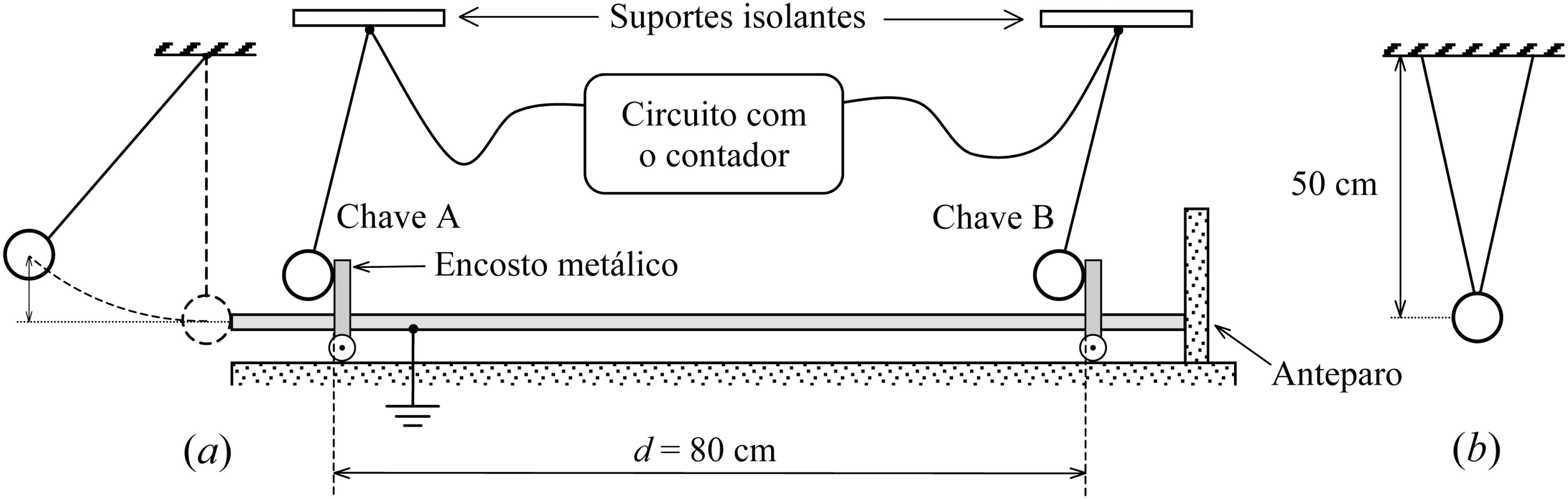
A Fig. 3a mostra esquematicamente a montagem experimental utilizada para medir a velocidade do som numa barra; ela foi inspirada naquela relatada por Meiners [25]. A barra, de $1∕2$ polegada de diâmetro, foi fixada firmemente em dois suportes vazados de latão, que servem de encosto para as esferas de aço (de diâmetro $\varphi$ = 38,1 mm e massa $m$ = 225,8 g) indicadas na figura. Cada uma dessas esferas é suspensa por dois fios metálicos (suspensão bifilar - Fig. 3b) fixados num suporte isolante. Nas esferas, os fios foram fixados usando a técnica da eletro-erosão [26]. Cada suporte de latão, por sua vez, se apóia num eixo com rolamentos, de modo que o conjunto, barra mais suportes de latão, constitui um carrinho com rolamentos.

Figura 3
$a)$ Arranjo mecânico utilizado para medir a velocidade de um pulso de compressão ao longo de uma barra fina; $b)$ suspensão bifilar das esferas.

Nessa montagem a extremidade direita da barra encosta num anteparo para que não saia de sua posição original após cada pancada dada na sua extremidade esquerda. Essas pancadas (suaves) podem ser produzidas soltando a esfera à esquerda da figura ($\varphi$ = 27,0 mm e $m$ = 80,2 g), também suspensa por dois fios.

O princípio do método é relativamente simples. A esfera e o encosto metálico constituem uma chave. Enquanto a esfera estiver em contato com o encosto, a chave está fechada; quando o contato é desfeito, a chave se abre. Por causa da inércia das esferas, a primeira chave (chave A) abre-se momentaneamente logo que o pulso de compressão, propagando-se ao longo da barra, passa por ela; passados $t$ segundos abre-se momentaneamente a segunda chave (chave B). Tendo-se o tempo $t$ (tempo de voo) e a distância entre as chaves, determina-se então a velocidade $c=d∕t$ de propagação do pulso.

O desafio é como medir $t$, pois o contador deve iniciar o registro dos pulsos enviados por um oscilador a cristal com a abertura momentânea da chave A e interromper a contagem com a abertura momentânea da chave B. Mas, além disso, o retorno de cada esfera para sua posição inicial logo após a passagem do pulso por ela não pode interferir no funcionamento do contador. O circuito projetado para satisfazer a essas condições está representado esquematicamente na Fig. 6. Para entender mais facilmente o seu funcionamento é conveniente descrever primeiramente como funcionam os circuitos integrados CD4013 e CD4066 que usamos para montá-lo.

3.2. O circuito flip-flop (CD 4013)

O flip-flop é um circuito cuja saída permanece estável em um de dois estados possíveis. O estado em que está depende do que aconteceu anteriormente no circuito; ele tem “memória”. Pode ser montado com transistores, portas lógicas ou comprados já prontos para o uso. O CD4013BE, que utilizamos, é um integrado de 14 pinos que contem dois flip-flops independentes (Fig. 4). Cada um deles tem quatro entradas (CL, D, R, S) e duas saídas ($Q$ e $\overline{Q}$); a barra sobre a letra significa que o nível lógico dessa saída é sempre oposto ao da outra, i.e, $Q$ e $\bar{Q}$ têm níveis lógicos opostos. Das quatro entradas, as que nos interessam são apenas R e S; as entradas não utilizadas, CL e D, devem ser aterradas. Os terminais 7 e 14 são respectivamente terra e alimentação. A maneira como um flip-flop funciona é determinada por meio da tabela verdade fornecida pelo fabricante. No nosso caso, basta saber interpretar essa tabela para usar o flip-flop; não é necessário conhecer detalhes do circuito. A Fig. 4 mostra, esquematicamente, o CD4013 com seus dois flip-flops independentes e uma “tabela verdade” simplificada, que foi construída a partir daquela fornecida pelo fabricante.

Figura 4
$a)$ O CD4013 com seus dois flip-flops independentes; $b)$ tabela verdade simplificada.

Imaginemos, inicialmente, que os níveis lógicos de R, S, $Q$ e $\bar{Q}$ são, respectivamente, 0, 0, 0 e 1 como mostra a primeira linha da tabela. A chegada de um pulso na entrada S faz as saídas do flip-flop mudarem de estado; o nível lógico de $Q$ vai de 0 para 1 enquanto o nível lógico de $\bar{Q}$ vai de 1 para 0. A característica importante do circuito flip-flop é que essas saídas permanecem nesses estados, mesmo que cheguem mais pulsos nessa entrada (que no caso é a entrada S). A única maneira de voltar à situação original é enviar um pulso para a outra entrada, ou seja, para a entrada R, como mostra a terceira linha da tabela. Por causa dessa característica de funcionamento o flip-flop pode ser utilizado, por exemplo, para disparar/paralisar eletronicamente um contador eletrônico [27].

3.3. A chave digital (CD4066)

O CD4066 é um dispositivo que contem quatro chaves digitais bilaterais. Essas chaves funcionam como um interruptor comum; têm dois terminais para entrada/saída e um terminal de controle para ligar/desligar a chave. Quando o nível lógico nesse terminal é 0, a chave está aberta, e quando é 1, está fechada. As chaves e seus terminais estão representados na Fig. 5. Esse integrado é alimentado através do terminal 14, com o terminal 7 aterrado.

Figura 5
O CD4066 e suas quatro chaves independentes. Como utilizamos somente três chaves, apenas um CD4066 foi suficiente para montar o circuito da Fig. 6; os terminais das chaves não utilizadas devem ser aterrados.

3.4. Circuito para medir o tempo de voo de pulso na barra

Uma vez conhecido o funcionamento dos componentes 4013 e 4066, podemos entender melhor como o circuito esquematizado na Fig. 6 funciona. Com relação ao contador digital nesse esquema, é necessário conhecer apenas o papel de seus dois principais terminais (CL EN e CLOCK). O CLOCK é o terminal do contador que receberá os pulsos a serem contados. O CL EN é o terminal responsável por habilitar/desabilitar a contagem. Uma vez que o CL EN estiver em nível alto o dispositivo não irá contar mesmo que o CLOCK esteja recebendo pulsos continuamente. A contagem só terá início quando o CL EN estiver em nível baixo (para mais detalhes ver a Ref. [27]). Os dois LED's foram colocados nas saídas Q${}_1$e Q${}_2$ para indicar seus níveis lógicos, pois ficarão acesos quando as saídas estiverem no nível alto.

Figura 6
Circuito projetado para medir o tempo de voo do pulso ao longo da barra.

Consideremos inicialmente as duas esferas indicadas na Fig. 6 em repouso em seus respectivos encostos metálicos e as saídas Q${}_1$ e Q${}_2$ do 4013 inicialmente em nível alto (LED's acesos). Se observarmos a segunda linha da tabela verdade simplificada do 4013 na Fig. 4b, veremos que nessas condições, i.e, Q${}_1$ e Q${}_2$ em nível alto, os terminais R${}_1$, S${}_1$e R${}_2$, S${}_2$ devem estar necessariamente em nível baixo, o que acontecerá depois que os resets 1 e 2 forem acionados. Como inicialmente Q${}_1$ está em nível alto, o pino 6 do 4066 também está alto. Isso quer dizer que a chave CH 3 entre os terminais 8 e 9 do 4066 está fechada, ou seja, o CLOCK do contador está recebendo os pulsos de 1 MHz gerados pelo cristal oscilador [27]. Entretanto, como o nível de Q${}_2$ também está inicialmente alto, o contador permanece paralisado, pois o CL EN está ligado a Q${}_2$. Por outro lado, como a barra está aterrada, tanto o pino 5 como o pino 13 do 4066 estarão em nível baixo, ou seja, as duas chaves (CH 1 e CH 2) estão inicialmente abertas.

Quando a barra é golpeada e o pulso chega na posição da primeira esfera, o contato entre ela e o encosto abre-se, embora de maneira imperceptível para um observador a olho nu. Quando isso acontece, o terminal 13 do 4066 vai para o nível alto e fecha momentaneamente CH 1, deixando R${}_2$ em nível alto. Então o nível lógico de Q${}_2$vai de 1 para 0, e conseqüentemente também o nível do CL EN. A partir desse ponto o contador dispara e começa a marcar o tempo em microssegundos. Inevitavelmente, a primeira esfera voltará a tocar o suporte abrindo a chave CH 1 do 4066 mudando assim o estado da entrada R${}_2$ para baixo novamente. Mas, como foi dito anteriormente, a característica principal do flip-flop é que a sua saída permanece estável mesmo que cheguem mais pulsos na mesma entrada. Assim, o fato da esfera encostar novamente no suporte não interfere no funcionamento do contador, pois Q${}_2$ continuará no nível baixo [28].

Enquanto o pulso estiver percorrendo a distância $d$ entre as chaves o contador estará marcando. Quando o pulso chega na posição onde está a segunda esfera, o contato entre ela e o suporte é desfeito momentaneamente. O terminal 5 do 4066 vai para o nível alto e fecha a chave CH 2, deixando R${}_1$ em nível alto. O nível lógico de Q${}_1$ vai então de 1 para 0. Essa alteração no nível de Q${}_1$ faz abrir a chave CH 3 do 4066, impedindo o CLOCK do contador de receber os pulsos enviados pelo cristal oscilador. Dessa forma a contagem cessa e o número registrado no painel do contador será exatamente o tempo, em microsegundos, que o pulso levou para percorrer a distancia $d$ entre as duas esferas. Em resumo: a primeira esfera controla o nível da entrada CL EN do contador, enquanto que a segunda controla o nível da entrada CLOCK. Para repetir o processo basta pressionar os resets 1 e 2. Com esta operação mudamos os estados das entradas S${}_1$ e S${}_2$ do 4013 e consequentemente também o estados dos terminais Q${}_1$ e Q${}_2$, deixando o sistema novamente na situação inicial.

4. Resultados

A Fig. 7 mostra o aspecto de um conjunto típico de 30 medidas do tempo gasto por um pulso (tempo de voo), propagando-se ao longo de uma barra de aço inox 304, para percorrer a distância de 80 cm entre as chaves A e B indicadas na Fig. 3. Para produzir as pancadas que geraram esses dados, a esfera à esquerda da Fig. 3 foi afastada cerca de 7 cm da extremidade da barra e liberada em seguida. Com um afastamento dessa ordem, a intensidade da pancada é suficiente para abrir as chaves e suave o bastante para não deformar permanentemente a barra. Vale mencionar que antes de iniciar o experimento é importante ajustar a montagem para que o impulso produzido pela esfera incidente seja aplicado no centro da extremidade da barra e na direção do seu eixo (o uso de papel carbono facilita esse ajuste). Com isso evitamos movimentos laterais da barra.

Figura 7
Conjunto típico de 30 medidas do tempo de voo obtido para uma barra de aço inox 304. Os pontos representam os dados experimentais e a linha sólida corresponde ao valor médio.

A velocidade do pulso determinada a partir do tempo de voo médio ($\bar{t}$ = 159,7 $\mu$s) e da distância entre as chaves ($d$ = 80 cm) resulta em $c$ = 5009 m/s. Esse valor praticamente coincide com aquele que obtivemos em outro trabalho utilizando um método diferente de medida [23] e também com a velocidade do som esperada em barras de aço inox 347, cuja massa específica é aproximadamente igual a do aço 304 [29]. Levando em conta o desvio padrão de $\bar{t}$ (${\sigma }_{\bar{t}}=0,9\mu$s) e considerando que a distância entre as chaves é conhecida com uma incerteza de $\pm$ 1 mm, podemos concluir que o resultado final para a velocidade do pulso nessa barra é igual a $c$ = (5009 $\pm$ 29) m/s.

O experimento foi repetido com uma barra de latão (de mesmas dimensões que a barra de aço) e depois com um sarrafo de madeira de seção retangular com dimensões de 31 mm por 34 mm. O resumo dos resultados obtidos e o módulo de Young calculado para cada um dos materiais estudados constam na Tabela 1.

Tabela 1
Resultados experimentais obtidos para diferentes materiais. $\bar{t}$: tempo de voo médio; ${\sigma }_t$: desvio padrão; ${\sigma }_{\bar{t}}$: desvio padrão da média; $c$: velocidade do som na barra; $\rho$: massa específica; $Y$: módulo de Young.

Material	$\bar{t}(\mu$s)	${\sigma }_t(\mu$s)	${\sigma }_{\bar{t}}(\mu$s)	$c$(cm/s)	$\rho$(g/${\text{cm}}^3)$	$Y(\times$${10}^{10}$${\text{N}}^2$/m)
Aço inox 304	159,7	5,0	0,9	5009 $\pm$ 29	7,88	19,8 $\pm$ 0,3
Latão*	231,5	8,3	1,5	3456 $\pm$ 23	8,44	10,1 $\pm$ 0,2
Madeira dura†	190,4	10,4	1,9	4204 $\pm$ 42	1,05	1,85 $\pm$ 0,04

• ^*
  Composição: 77% Cu e 23% Zn,
• ^†
  Maçaranduba

A velocidade do som numa barra de latão depende de sua composição. Segundo a literatura ela é igual a 3480 m/s se a barra é composta de 70% de cobre e 30% de zinco [29]. O resultado que se encontra na Tabela para o latão é compatível com esse valor, se considerarmos que a barra que utilizamos é composta por 77% de cobre e 23% de zinco. A velocidade do som em algumas espécies típicas de madeira de grande dureza e durabilidade e quando medida ao longo das fibras varia na faixa de 3850 m/s a 4670 m/s [29]. Como medimos a velocidade num sarrafo de maçaranduba, que também pertence à categoria das madeiras duras e duráveis, não causa estranheza o fato do resultado obtido (de 4204 m/s) estar nessa faixa. O módulo de Young, tanto para o aço inox 304 como para os demais materiais estudados, mostram boa concordância com as informações disponíveis na literatura [30,31].

5. Conclusões

Neste trabalho determinamos o módulo de Young de diferentes materiais a partir da velocidade de um pulso de compressão, propagando-se ao longo de uma barra fina, medida pelo método do tempo de voo. Esse tempo (correspondente ao tempo gasto para o pulso percorrer a distância conhecida entre dois sensores montados sobre a barra) foi medido por meio de um arranjo mecânico e um contador eletrônico conectado a um oscilador a cristal. Para isso, projetamos um circuito que permite disparar o contador com a passagem do pulso pelo primeiro sensor e paralisá-lo com a passagem pelo segundo. As incertezas estatísticas envolvidas no experimento foram calculadas para um conjunto de 30 medidas; tomando-se o desvio padrão da média para avaliação dos resultados, chega-se a uma incerteza próxima de 2% no cálculo do módulo de Young dos diferentes materiais estudados. A concordância entre os valores medidos e os reportados na literatura é bastante satisfatória.

A vantagem da técnica descrita aqui consiste não só na sua confiabilidade como também no fato de poder ser utilizada para estudar tanto amostras metálicas (aço, latão, etc.) como não-metálicas (por ex., madeira e PVC, entre outros). Além dos princípios físicos envolvidos em processos de colisão, o experimento introduz importantes conceitos de eletrônica ao apresentar o funcionamento de componentes vastamente utilizados em circuitos digitais. O tempo necessário para realização das medidas não é excessivo e os materiais necessários para montagem do arranjo mecânico e do contador digital podem ser facilmente encontrados no mercado, tornando o experimento particularmente apropriado para ser realizado em laboratórios de ensino de física básica.

Agradecimentos

Os autores agradecem à FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo) e ao CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) pelo apoio financeiro. Agradecem também aos servidores da UNESP, Claudio L. S. Bocaiuva e Geraldo Ap. de Lima Sobrinho, pelo apoio técnico.

Referências

• [1] U. Ingard and W.L. Kraushaar, Introduction to Mechanics, Matter, and Waves (Addison-Wesley Publishing Company, Inc., Massachussets, 1960), cap. 21.
• [2] J. Goldemberg, Física Geral e Experimental (Companhia Editora Nacional, São Paulo, 1970), 2ª ed., v. 1, p. 275-278 e p. 315-318.
• [3] F.W. Sears, M.W. Zemansky and H.D. Young, College Physics (Addison- Wesley Publishing Company, Inc., Massachussets, 1991), 7$th$ ed., cap. 12.
• [4] F. Wilson and A.E. Lord, Am. J. Phys. 41, 653 (1973).
• [5] P. Lucie, Física Básica - Mecânica 2 (Editora Campus Ltda, Rio de Janeiro, 1980). cap. 4 e cap. 5.
• [6] S. Tyagi and A.E. Lord Jr, Am. J. Phys. 48, 205 (1980).
• [7] W.H. Westphal, Práticas de Física (Editorial Labor S.A., Barcelona, 1965).
• [8] R.M. Whittle and J. Yarwood, Experimental Physics for Students (Chapman and Hall Ltd, London, 1973).
• [9] F. Tyler, A Laboratory Manual of Physics (Edward Arnold Publishers Ltd, London, 1974), 4${}^{th}$ ed.
• [10] L.R. Gomes, A. Amado, M.C. Torres and L.M.N.B.F. Santos, Phys. Teach. 49, 117(2011).
• [11] J. Goldemberg, Física Geral e Experimental(Companhia Editora Nacional, São Paulo, 1970), 2ª ed., v. 1, p. 489-491.
• [12] K. Turney, Am. J. Phys. 58, 483 (1990).
• [13] D. Potter, Phys. Teach. 40, 56 (2002).
• [14] G.B. Karshner, Am. J. Phys. 57, 920 (1989).
• [15] O. Ames, Am. J. Phys. 38, 1151 (1970).
• [16] T. Key and R. Smidrovskis, Phys. Teach. 38, 76 (2000).
• [17] C.K. Manka, Am. J. Phys. 37, 223 (1969).
• [18] J.C. Albergotti, Am. J. Phys. 49, 595, (1981).
• [19] B.E. Martin, Phys. Teach. 39, 424 (2001).
• [20] S.Y. Mak, Y.K. Ng and K.W. Wu, Phys. Ed. 35, 439 (2000).
• [21] G.P. Hart, Phys, Teach. 24, 89 (1986).
• [22] R.C. Nicklin, Am. J. Phys. 41, 734 (1973).
• [23] A.A. Freschi, R. Hessel, M. Yoshida and D.L. Chinaglia, Am. J. Phys. 82, 280 (2014).
• [24] K.F. Graff, Wave Motion in Elastic Solids (Dover Publication, Inc., New York, 1991), Item 2.3.1.
• [25] Physics Demonstration Experiments, edited by H.F. Meiners (Ronald Press Company, New York, 1970), v. I, p. 490-492.
• [26] R. Hessel, A.C. Perinotto, R.A.M. Alfaro and A.A. Freschi, Am. J. Phys. 74, 734 (2006).
• [27] R. Hessel, C.S. de Oliveira, G.A. Santarine e D.R. Vollet, Revista Brasileira de Ensino de Física 30, 1501 (2008). Erratum 31, 4901 (2009).
• [28] P. Horowitz and W. Hill, The Art of Eletronics (Cambridge, Cambridge University Press, 1980), p. 342.
• [29] CRC Handbook of Chemistry and Physics, edited by R.C. Weast (CRC Press, Inc., Boca Raton, 1986), 67th ed., p. E-43.
• [30] H.M. Ledbetter, N.V. Frederick and M.W. Austin, J. Appl. Phys. 51, 305 (1980).
• [31] N. Koshkin and M. Shirkevich, Handbook of Elementary Physics (MIR, Moscow, 1968), p. 45.

Datas de Publicação

• Publicação nesta coleção
  Jun 2016

Histórico

• Recebido
  08 Dez 2015
• Aceito
  10 Fev 2016