Determinación del módulo de Young de una barra cilíndrica

Determination of Young's modulus of a cylindrical bar

Resúmenes

El siguiente trabajo hace uso de los teléfonos inteligentes para determinar el módulo elástico o módulo de Young de una barra cilíndrica de Latón utilizando dos sensores: El micrófono, para determinar las frecuencias transversales componentes de la oscilación de la barra prensada en un extremo y libre en el otro, y el sensor de aceleración para determinar la frecuencia de oscilación de una masa sujeta al extremo de la barra, usando el teléfono como masa inercial. Se comparan ambos métodos entre sí y con el valor de referencia [¹] para el módulo de Young del material.

Palabras clave:
Vibraciones; modos normales de sistemas continuos; Módulo de Young; Física con teléfonos inteligentes

The following work makes use of smartphones in order to determine the elasticity modulus or Young's modulus of a cylindrical brass bar (copper-zinc alloy), employing two different devices: A microphone, to determine the components frequencies of the bar's oscillation, which is compressed at one end and free at the other, and an accelerometer to calculate oscillation frequency of a body attached to the end of the bar (using the phone as an inertial mass). Both methods are compared to each other, and with the reference value for the Young's modulus belonging to the material.

Keywords:
Vibrations; normal modes for continuos systems; Young's modulus; physics with smartphones

1. Introducción

El análisis de las vibraciones libres de una estructura es de fundamental importancia para los estudiantes de diferentes niveles. En este caso, el presente trabajo está orientado a la formación de futuros profesores de enseñanza media, que a su vez serán profesores de futuros profesionales en las distintas áreas técnicas, artísticas o de la ingeniería.

Una estructura vibrando libremente presenta diferentes modos de oscilación denominados modos normales [²], caracterizados por un conjunto de frecuencias propias que dependen en general de las diferentes condiciones de contorno a las que está sometida la estructura. En nuestro caso estudiaremos la frecuencia fundamental de la oscilación transversal para diferentes longitudes de una barra prensada en un extremo y libre en el otro golpeada con un martillo de goma[³].

Las frecuencia fundamental presente en la vibración de la barra se obtienen haciendo uso de las herramientas disponibles en los teléfonos inteligentes, el micrófono permite mediante la transformada de Fourier obtener el espectro de la potencia acústica radiada por la barra vibrante y así obtener la frecuencia fundamental. (Además de las frecuencias naturales superiores) En una segunda experiencia hacemos uso del sensor de aceleración para hallar la frecuencia de oscilación de una masa sujeta al extremo de una barra, para diferentes longitudes de la barra (usando el teléfono como masa inercial).

2. El experimento

2.1. Vibración de una barra prensada-libre

Se utilizó una barra de latón de una aleación de 70% cobre y 30% Zinc de las siguientes dimensiones:

Largo $L=\left(1,040\pm 0,001\right)m$ (medido con cinta métrica milimetrada);

Diámetro $D=\left(3,97\pm 0,01\right)mm$ (medido con micrómetro);

Masa $m=\left(108,98\pm 0,01\right)g$ (medido con balanza digital a la centésima de gramo).

Las frecuencias fundamentales para las diferentes longitudes (variado la longitud prensando la barra en diferentes posiciones) se obtuvieron golpeando la barra de la Figura 1 cerca de donde está prensada y con un golpe en dirección perpendicular a la misma, de forma de excitar los distintos modos transversales de la barra (ver Figura 2). El sonido emitido se registró y analizó en tiempo real mediante la FFT (Fast Fourier Transform) con la aplicación Spectrum Analyser[⁴].

Figura 1
Barra cilíndrica prensada mediante una morsa.

Figura 2
Modos transversales de vibración de una barra

3. Fundamento teórico

Las frecuencias transversales de una barra prensada-libre de longitud $L$ vienen dadas por la siguiente expresión [³]:

(1) $$f=\frac{\pi c\kappa }{8L^2}\left(1,194^2,2,988^2,5^2,7^2,...\right)$$

Donde $c=\sqrt{\frac{E}{\rho }}$ es la velocidad de fase para las ondas longitudinales, $E$ es el módulo de Young y $\rho$ es la densidad de masa del material. La constante $\kappa$ denominada radio de giro está definida a partir de:

(2) $${\kappa }^2=\frac{{\int }_S{r}^{2}ds}{S}$$

Donde $r$ es la distancia de un elemento de áreas ds al eje neutro de una sección transversal cualquiera de la barra y $S$ representa el área de dicha sección. En nuestro caso $\kappa =\frac{D}{4}$ ¹ siendo $D$ el diámetro de la barra. A partir de la ecuación 1 la frecuencia fundamental para una barra prensada-libre está dada por:

(3) $$f_1\approx \frac{0,14D}{L^2}\sqrt{\frac{E}{\rho }}$$

4. Resultados experimentales

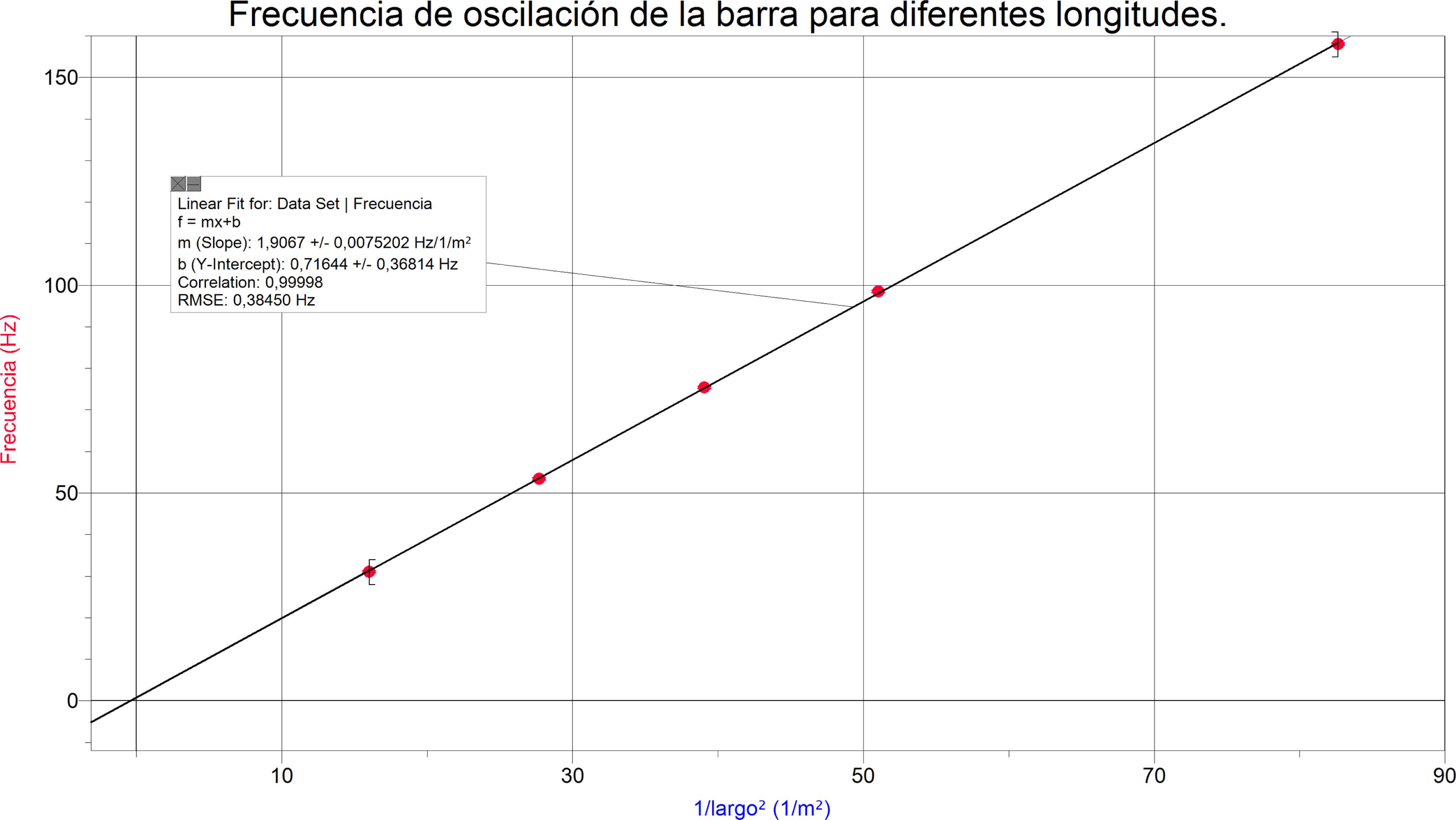
Los datos obtenidos se resumen en el cuadro (ver tabla 1) y la gráfica siguiente:

Tabla 1
Frecuencias de vibración de una barra prensada en un extremo para diferentes longitudes de la misma.

$\left(L\pm 0,5\times 10^{-3}\right)m$	$\left(f_1\pm 0,3\right)\left(Hz\right)$	$f_1{L}^2\left(Hz{m}^2\right)$
0,1100	158,0	1,912
0,1400	98,5	1,931
0,1600	75,4	1,929
0,1900	53,4	1,927
0,2500	31,0	1,938

La pendiente del gráfico $f=F\left(1∕L^2\right)$ determinada por mínimos cuadrados es:

$$f{L}^2\approx \left(1,907\pm 0,026\right)Hz{m}^2$$

La incertidumbre en la pendiente se calculó propagando incertidumbres en la ecuación² (3)

En el gráfico de la Fig. 3 se puede apreciar que la frecuencia de oscilación es directamente proporcional al inverso de su longitud al cuadrado en acuerdo con el modelo teórico resumido en la ecuación 1. En dicha ecuación podemos observar que las distintas frecuencias no son armónicas de la frecuencia fundamental sino que están en una relación:

(4) $$f_1,6,267f_1,17,55f_1,34,39f_1,...$$

Figura 3
Gráfico de la frecuencia en función del inverso de la longitud de la barra al cuadrado.

Las frecuencias de la tabla 1 se obtuvieron mediante la aplicación Spectrum Analyser [⁴] golpeando la barra. La misma fue prensada mediante una morsa de metal fija a una mesa de madera. Dicha aplicación nos da una ventana donde se observa la FFT (El espectro de potencia o transformada rápida de Fourier) en tiempo real de la señal de audio captada mediante el micrófono del teléfono inteligente. Dicha aplicación permite ajustar diferentes parámetros, la frecuencia de muestreo, el número de puntos de la FFT, el tipo de ventana para la FFT (Bartlett, Blackman, Hanning, Flat Top, etc), el intervalo de tiempo (250ms,500ms,1000ms) lo que permite obtener diferentes resoluciones en frecuencia.

Para largos de la barra mayores a 20cm el espectro de Fourier no permite determinar la frecuencia fundamental directamente, ya que dicha frecuencia al ser muy baja (menor a 50Hz a partir de consideraciones teóricas) radia una potencia acústica muy pequeña y no aparece un pico correspondiente a dicha frecuencia en la FFT. Sí es posible obtener las frecuencias de los modos superiores y determinar indirectamente $f_1$ a partir de la ecuación (4).

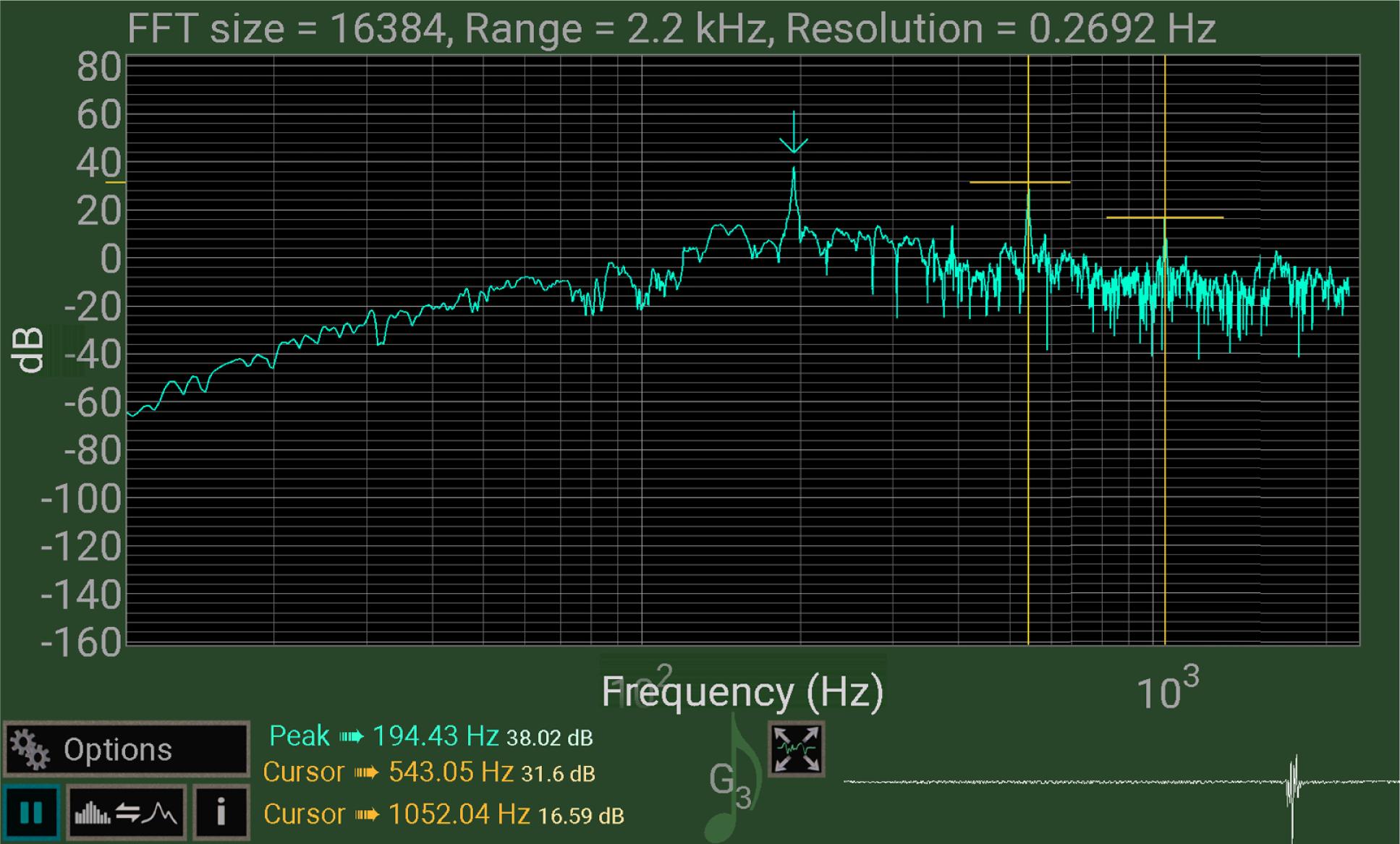
En la Figura 4 se aprecian tres picos que corresponden a las frecuencias $f_2$, $f_3,f_4$ y no se aprecia la frecuencia fundamental ($f_1$ es menor a 50Hz), ya que las frecuencias:

$$\frac{f_3}{f_2}=\frac{543Hz}{194,4Hz}\approx 2,793$$

Figura 4
Ventana gráfica de la FFT en tiempo real de la vibración de la barra para una largo de 25,00cm. Se superpusieron dos fotogramas para determinar las frecuencias de los armónicos $f_3$ y $f_4$.

que están aproximadamente en la misma relación que la teórica (ver ecuación 4):

$$\frac{f_3}{f_2}=\frac{17,55}{6,267}\approx 2,80$$

Luego la frecuencia fundamental es en este caso:

$$f_1=\frac{f_2}{6,267}=\frac{194.4Hz}{6,267}=31,0Hz$$

La frecuencia $f_3$ estaría entonces dada por:

$$f_3=17,55f_1=17,55\times 31,0Hz\approx 544Hz$$

Y finalmente la frecuencia $f_4$ estaría dada por:

$$f_3=34,39f_1=34,39\times 31,0Hz\approx 1066Hz$$

Valores calculados que coinciden aproximadamente con los valores medidos experimentalmente (543Hz y 1052Hz respectivamente) (ver Figura 4).

Para largos de la barra pequeños el espectro permite determinar con precisión la frecuencia fundamental como se puede apreciar en la ventana gráfica de la aplicación Spectrum Analyser[⁴].

Los parámetros utilizados en este caso son: frecuencia de muestreo de 2,2kHz, un número de puntos de la FFT de 16384 (número de datos para construir la transformada rápida de Fourier) ventana Hanning e intervalo de 500ms. Esta combinación de frecuencia de muestreo y número de puntos (FFT range y FFT size) dan una resolución en frecuencia de 0,27Hz como se aprecia en la Figura 5.

Figura 5
Captura de pantalla de la aplicación Spectrum Analyser, correspondiente a un largo de la barra de 11,0cm.

5. Determinación del módulo de Young a partir de los datos del experimento

La pendiente del gráfico $f=F\left(1∕L^2\right)$ está dada a partir de la ecuación 4 por:

$$f_1{L}^2\approx 0,14D\sqrt{\frac{E}{\rho }}\approx \left(1,907\pm 0,024\right)Hz{m}^2$$

La densidad de la barra de acuerdo a las medidas de sus longitudes y masa tiene el valor aproximado de:

$$\begin{array}{rcll}\rho & =& \frac{m}{\frac{\pi D^2}{4}L}=\frac{108,98\times 10^{-3}kg}{\frac{\pi \times {\left(3,97\times 10^{-3}m\right)}^2}{4}\times 1,040m}& \\ & \approx & 8,47\times 10^{3}kg∕m^3& \end{array}$$

Luego a partir de la ecuación 4 obtenemos para el módulo de Young el valor³

$$E\approx \left(10,0\pm 0,2\right)\times 10^{10}N∕m^2$$

El valor de la densidad y el módulo de Young del Latón son de acuerdo http://www.makeitfrom.com/material-properties/UNS-C85800-Leaded-Yellow-Brass:

$$\begin{array}{c}\rho =8,4\times 10^{3}kg∕m^3\hfill \\ E=10,0\times 10^{10}N∕m^2\hfill \\ \hfill \end{array}$$

Por lo cual los valores medidos son consistentes con los valores de referencia.[¹]

6. Determinación del módulo de Young mediante la medida de la frecuencia de oscilación de una masa en el extremo de una barra

En la figura 6 se observa el dispositivo utilizado. Se suspendió del extremo libre de la barra prensada una masa $m$ (El teléfono inteligente) y se le imprimió una pequeña oscilación vertical, dando lugar a una oscilación amortiguada (ver figura 7).

Figura 6
Dispositivo experimental para determinar el módulo elástico de una barra delgada larga.

Figura 7
Aceleración vertical del teléfono inteligente en función del tiempo para un largo de la barra de 60,0cm.

Se utilizó la aplicación Physics Toolbox Sensor Suite [⁵] a modo de “Data Logger”. Se envió el archivo de datos en forma de tabla y luego se procesó usando el Logger Pro. Dicha aplicación envía la tabla de datos en forma de columnas, la variable de interés es la aceleración en el eje $y$ (la cual está expresada en múltiplos de la aceleración de la gravedad más la componente de la aceleración gravitatoria $g$, en la dirección vertical)[⁶,⁷]

Supongamos la oscilación amortiguada anterior es de la forma:

(5) $$x=Aexp\left(-\frac{\gamma }{2}t\right)cos\left(\omega t+\delta \right)$$

Donde ${\omega }^2={\omega }_0^2-\frac{{\gamma }^2}{4}$ siendo ${\omega }_0$ la frecuencia angular de la oscilación libre no amortiguada.

La aceleración está dada derivando dos veces respecto del tiempo por:

(6) $$\begin{array}{rcll}a& =& Aexp\left(-\frac{\gamma }{2}t\right)\left[\right.\omega \gamma sen\left(\omega t+\delta \right)& \\ & -& \left({\omega }^2-\frac{{\gamma }^2}{4}\right)cos\left(\omega t+\delta \right)\left]\right.\end{array}$$

Como en general $\gamma$ es pequeño comparado con $\omega$ se puede despreciar el primer término dentro del paréntesis recto, por lo cual la aceleración se aproxima al siguiente valor:

(7) $$a=-{\omega }^{2}Aexp\left(-\frac{\gamma }{2}t\right)cos\left(\omega t+\delta \right)$$

Mediante el Logger Pro ajustamos los datos experimentales con la expresión anterior para obtener la frecuencia de oscilación para diferentes longitudes de la barra.

La frecuencia de la oscilación de una masa $m$ en el extremo libre de una barra prensada de largo $L$ y área de sección transversal $S$ viene dado por:⁴

$$f=\frac{1}{2\pi }\sqrt{\frac{3ES}{m{L}^3}}\kappa$$

En el caso de una barra de sección circular de diámetro $D$ la expresión anterior es:

$$f=\frac{0,0611\times D^2}{L^{3∕2}}\sqrt{\frac{E}{m}}$$

7. Resultados experimentales

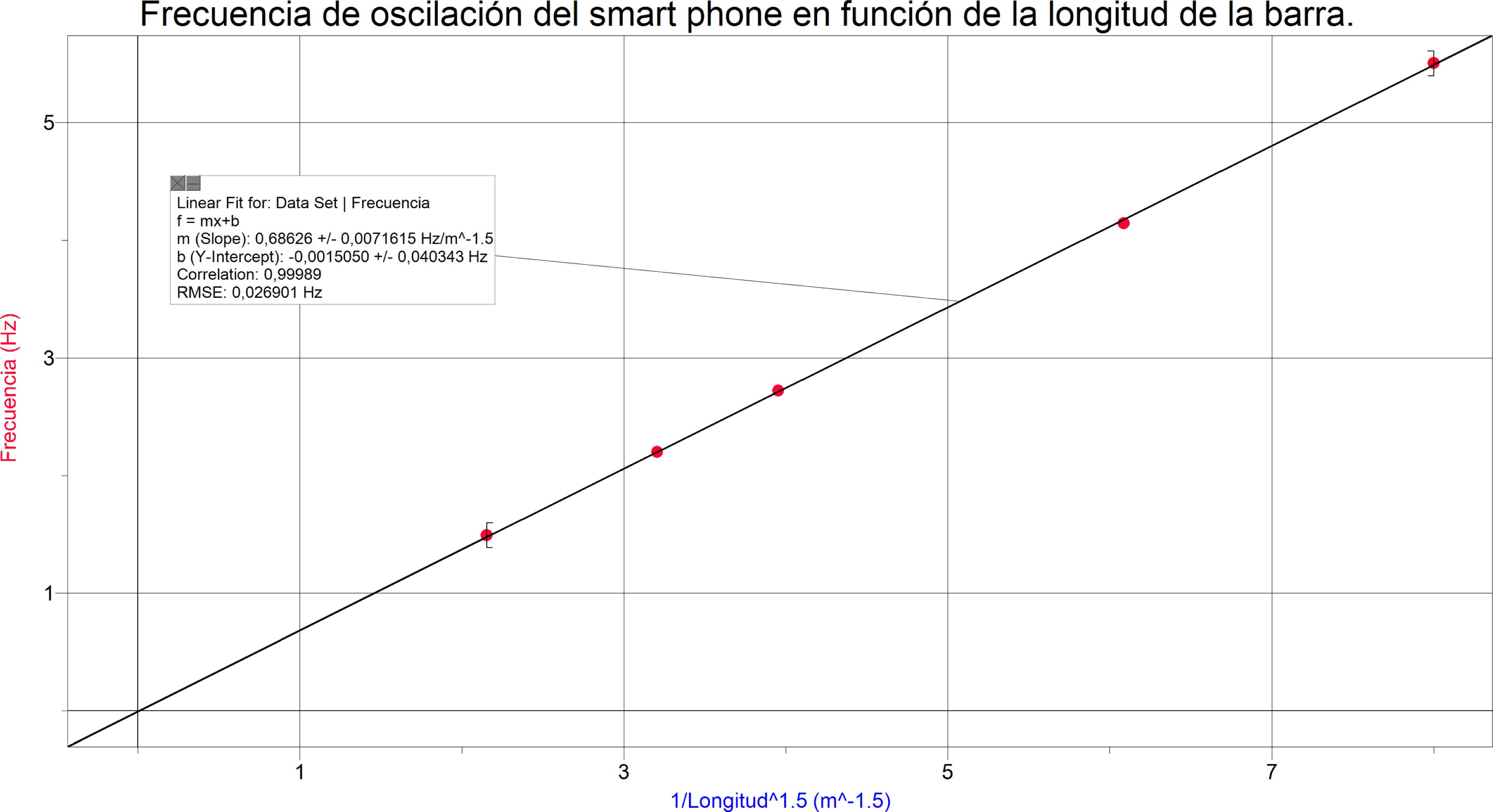
La experiencia anterior se resume en la tabla 2 y la gráfica siguientes:

Tabla 2
Frecuencias de vibración de una masa en el extremo de una barra prensada.

$\begin{array}{c}\hfill \left(L\pm 0,001\right)\left(m\right)\hfill \\ \hfill \hfill \end{array}$	$\left(f\pm 0,001\right)\left(Hz\right)$	fL ${}^{3∕2}$ (Hzm ${}^{3∕2})$
0,250	5,506	0,688
0,300	4,143	0,681
0,400	2,722	0,689
0,460	2,202	0,687
0,600	1,493	0,694

El modelo teórico queda confirmado a partir del gráfico de la figura 8 frecuencia en función del inverso de la longitud de la barra elevado a 3/2.

Figura 8
Frecuencia de oscilación del teléfono inteligente para diferentes longitudes de la barra.

En dicha gráfica y en la tercera columna de la tabla 2 se observa que la frecuencia de oscilación de la masa es directamente proporcional a $L^{3∕2}$, la pendiente de dicho gráfico es de acuerdo al modelo teórico:

$$f{L}^{3∕2}=0,0611D^2\sqrt{\frac{E}{m}}\approx \left(0,686\pm 0,007\right)Hz{m}^{3∕2}$$

Teniendo en cuenta que el valor de la masa $m$ es de $\left(195,30\pm 0,01\right)g$ (masa que incluye el teléfono y un estuche para el mismo) y la ecuación 9, el módulo de Young de la barra es⁵:

$$E\approx \left(9,9\pm 0,2\right)\times 10^{10}N∕m$$

8. Conclusiones

El objetivo del presente trabajo fue hacer uso del teléfono inteligente como herramienta alternativa no restringida al laboratorio tradicional. Se utilizó el micrófono como sensor de audio y la aplicación Spectrum Analyser para hacer la FFT en tiempo real de la señal acústica obtenida al golpear una barra delgada larga prensada en un extremo y libre en el otro. Se utilizó el sensor de aceleración para registrar el movimiento de una masa sujeta al extremo de una barra (el teléfono como masa inercial) y la aplicación Physics Toolbox Sensor Suite a modo de “Data Logger”. Los datos exportados desde la aplicación fueron analizados usando la aplicación Logger Pro de Vernier (se pudo hacer uso también de varias aplicaciones disponibles para teléfonos, como Vernier graphical analysis, Sparkvue Pasco, etc.).

Los valores obtenidos por ambos métodos son comparables al valor de referencia[¹] y entre sí y a métodos usando otras herramientas disponibles en un laboratorio tradicional (micrófono externo con aplicaciones de análisis de audio como Audacity, sensores de aceleración o de fuerza de la Vernier)

Módulo de Young. Oscilación de la barra prensadalibre. Oscilación de la masa. Valor de referencia.[1] E ( × 1 0 10 N ∕ m 2 ) 10,0 ± 0,2 9,9 ± 0,2 10,0

Módulo de Young.	Oscilación de la barra prensadalibre.	Oscilación de la masa.	Valor de referencia.[1]
$E\left(\times 10^{10}N∕m^2\right)$	$\text{10,0}\pm \text{0,2}$	$\text{9,9}\pm \text{0,2}$	10,0

Material suplementario

El siguiente material suplementario está disponible en línea:

Anexo 1

Referencias

• ^[1]
  ASTM, ASTM B176-17 - Standard Specification for Copper-Alloy Die Castings (ASTM International, West Conshohocken, 2017), www.astm.org.
  » www.astm.org
• ^[2]
  A.P. French, Vibraciones y Ondas (E. Reverté, Barcelona, 1974).
• ^[3]
  L.E. Kinsler, A.R. Frey, A.B.C. Coppens and J.V. Sanders, Fundamentos de Acústica (Ed. Limusa, México 1995).
• ^[4]
  Aplicación Spectrum Analyser, en línea http://www.keuwl.com/SpectrumAnalyser/
  » http://www.keuwl.com/SpectrumAnalyser/
• ^[5]
  Aplicación Physics Toolbox Sensor Suite, en línea https://play.google.com/store/apps/details?id=com.chrystianvieyra.physicstoolboxsuite&hl=es_419
  » https://play.google.com/store/apps/details?id=com.chrystianvieyra.physicstoolboxsuite&hl=es_419
• ^[6]
  Monteiro, Martín, Cabeza, Cecilia and Marti, Arturo C. Rev. Bras. Ens. Fis. 37, 1303 (2015).
• ^[7]
  Martín Monteiro, Cecilia Cabeza y Arturo C. Martí, Educación en Física 8, 15 (2016).
• ^[8]
  Salvador Gil, Experimentos de Física Usando las TIC y Elementos de Bajo Costo (Ed. Alfaomega, Buenos Aires, 2014).

• 1
  Ver anexo 1.
• 2
  Ver anexo 1.
• 3
  Ver anexo 1 para el cálculo de la incertidumbre.
• 4
  Ver anexo 1.
• 5
  Ver anexo 1 para el cálculo de la incertidumbre.

Fechas de Publicación

• Publicación en esta colección
  2018

Histórico

• Recibido
  10 Jun 2017
• Revisado
  23 Ago 2017
• Acepto
  03 Set 2017