Resumo
Neste artigo buscamos apontar alguns aspectos que diferenciam as Feynman lectures de livros tradicionais de física, com o objetivo de extrair princípios didáticos gerais que possam guiar uma discussão mais fundamentada sobre o que entendemos por qualidade no ensino de física.
Palavras-chave:
Lições de Feynman; Ensino de Física; Qualidade de Explicações; Relação entre Matemática e Física
Abstract
In this work an attempt is made to caracterize aspects that distinguish the Feynman lectures from traditional physics textbooks. The goal is to extract general didactical principles and contribute to a more informed discussion about quality in physics teaching.
Keywords:
Feynman lectures; Physics teaching; Quality of explanations; Mathematics in Physics
1. Introdução
É muito difícil encontrar alguém que se interesse por física que não tenha uma relação de fascínio com os livros vermelhos das Feynman lectures. Basta iniciar uma conversa informal sobre o assunto para ouvir frases do tipo: “foi no Feynman que entendi isso de verdade” ou “quando tenho que ensinar esse tópico sempre dou uma olhada no Feynman”, etc. Sem dúvida, as lectures são uma verdadeira obra-prima da didática, provavelmente o melhor livro-texto de física de todos os tempos. O próprio Feynman reconheceu que elas foram sua maior contribuição para a física. Mas afinal, o que faz as lectures serem tão especiais?
A resposta curta e fácil é que Feynman era genial. Ele foi um autodidata que tinha um hábito de questionar profundamente as coisas aparentemente mais banais e uma habilidade ímpar de comunicar com clareza. Sua atitude foi sempre de independência e repúdio a autoridades, com frequência ele reinventou teoremas e renomeou conceitos à sua maneira. Isso torna sua exposição extremamente original e, implicitamente, nos convida a pensar de maneira autônoma. Além disso, ele era extremamente carismático, assistir sua performance é uma experiência emocionante e contagiante. Podemos encontrar muitos outros elogios, mas essa atitude de reverenciar Feynman coloca-nos numa posição de impotência e assume que a arte de ensinar seja uma espécie de dom. Para quem pensa sobre o ensino da física essa postura é desmotivante, pois de certa forma implica que nascemos ou não professores. Assim, será que mesmo não sendo um Feynman, podemos extrair lições didáticas mais abrangentes das lectures para sermos melhores professores de física?
Tomando como premissa uma resposta positiva, o objetivo deste artigo é fazer uma análise mais sistemática sobre a qualidade didática do discurso das Feynman lectures, buscando extrair alguns princípios gerais que guiam sua construção. Adoto como ponto de partida um estudo com objetivos semelhantes que desenvolvi em minha tese de doutorado [1[1] R.A.S. Karam, Estruturação matemática do pensamento físico no ensino: uma ferramenta teórica para analisar abordagens didáticas. Tese de Doutorado, Universidade de São Paulo, São Paulo (2012).,2[2] R.A.S. Karam, Phys. Rev. ST Phys. Educ. Res. 10, 010119 (2014).]. Na referida pesquisa, propus um conjunto de categorias associadas à forma como a relação entre matemática e física é abordada em um discurso didático e as utilizei para analisar as aulas de eletromagnetismo de um professor experiente e muito apreciado por seus alunos. Muitos dos critérios associados à qualidade didática das aulas analisadas são facilmente encontrados no discurso do Feynman.
É preciso estar ciente das limitações deste projeto. De fato, o mesmo é, por definição, incompleto, pois existem inúmeros aspectos que podem ser analisados ao tentar entender por que as lectures são a maior obra-prima da didática da física. Não será possível, por exemplo, fazer uma discussão detalhada da estruturação conceitual dos capítulos. Em geral, é possível perceber que a ordem e a ênfase dos conceitos apresentados são diferentes das abordagens tradicionais. Por exemplo, ao introduzir a relação entre trabalho e energia, Feynman enfatiza a “relativamente desconhecida” equação (onde é a energia cinética) e deduz importantes resultados a partir dela. Tais diferenças são essenciais para entender a qualidade das lectures. Entretanto, é necessário um estudo detalhado de cada tópico para entendê-las profundamente e, além de impossível devido a limitações de espaço, estamos interessados em extrair princípios didáticos mais gerais.
Neste artigo, também não será tratado o contexto que motivou as lectures, uma vez que isso pode ser lido em seu Prefácio e em inúmeros artigos presentes na literatura, como o excelente relato feito por um dos idealizadores do projeto, Matthew Sands [3][3] M. Sands, Physics Today 58, 49 (2005).. Nosso objetivo é, portanto, discutir aspectos que distinguem as lectures de livros tradicionais.1 1 Por “tradicionais” entendemos clássicos como Halliday, Resnick e Walker; Tipler e Mosca; Sears e Zemansky; Young e Freedman; e similares. Usualmente, tais livros são destinados a um público bastante abrangente (inclusive engenheiros) e são muito semelhantes em sua forma e conteúdo. Para isso, faremos uso de alguns exemplos extraídos das lectures, cuja escolha tem, naturalmente, um grau de aleatoriedade. Não se trata de defender que tudo é melhor no Feynman (ainda que isso seja verdade na maioria dos casos), mas ressaltar as diferenças e discutir suas implicações didáticas e filosóficas. As citações e referências são extraídas da edição brasileira [4][4] R.P. Feynman, R.B. Leighton, M. Sands, Lições de física de Feynman: a edição definitiva. (Bookman, Porto Alegre, 2008), v. 3, p. 1798..
2. Diferenças à primeira vista
Basta uma rápida folheada pelas lectures para perceber algumas diferenças notáveis quando as comparamos com livros-texto de física mais tradicionais. Essas diferenças perceptíveis à primeira vista já indicam que se trata de uma proposta didática alternativa com objetivos distintos.
-
Muito texto
Ao abrir uma página aleatória, normalmente nos deparamos com uma quantidade enorme de texto corrido, quase que como se tivéssemos aberto um livro de romance. Uma explicação para isso é o fato de que o texto é resultado de uma transcrição, quase ipsis litteris, das lectures. Mas essa quantidade de texto também indica que Feynman prioriza uma abordagem conceitual, são raras as vezes em que equações são apresentadas sem que parágrafos de textos explicativos apareçam entre elas. Além disso, Feynman é extremamente metacognitivo em seu discurso e com frequência discute aspectos epistemológicos da física, o que naturalmente é expresso na forma de texto.
-
Ausência de “problemas”
Em abordagens didáticas tradicionais, é muito comum encontrar exemplos de “problemas resolvidos” no decorrer do discurso didático. Implicitamente, isso indica um foco na resolução de problemas e condiciona o estudante a se preparar para exercícios que serão cobrados em avaliações, o que muitas vezes o desvia de buscar uma profunda compreensão conceitual. As Feynman lectures são fundamentalmente diferentes neste aspecto. Não há sequer um “problema resolvido” nos três volumes. Tão pouco encontramos listas de exercícios no final dos capítulo 2 2 Isso tem sido motivo de críticas à funcionalidade das lectures e é uma possível razão pela qual elas não são comummente adotadas como livro-texto. Buscando responder a tais demandas, alguns volumes com listas de problemas para acompanhar as lectures foram publicados. Uma análise comparativa da natureza desses problemas pode ser outro caminho para indicar diferenças importantes em relação aos livros tradicionais. . O objetivo é claramente introduzir o estudante à maneira de pensar característica da física.
-
Fenomenologia
Uma das diferenças mais marcantes é a constante preocupação de Feynman em preencher de fenomenologia os conceitos e teorias que ensina. Física é uma ciência que lida com modelos idealizados da natureza, logo, para o inciante ela pode parecer algo artificial, desconexo da realidade. Feynman procura sempre restabelecer essa conexão; aplicações tecnológicas e aparatos experimentais estão presentes em quase todos os capítulos das lectures. O leitor pode argumentar que outros livros-texto também têm essa preocupação, mas julgo que as lectures discutem fenomenologia com muito mais frequência e de maneira muito mais autêntica. Um simples exemplo: no estudo da radiação eletromagnética (Cap. 28, Vol. 1), Feynman apresenta um aparato com dois fios ligados a um gerador (Fig. 28-1). Assim, em vez de imaginar um dipolo oscilante de maneira abstrata como cargas elétricas em movimento periódico, o estudante tem imediatamente uma noção de como isso pode ser realizado na prática.
Uma breve folheada pelo Volume 2 (Eletromagnetismo) é suficiente para encontrar diversos outros exemplos de tais vínculos estreitos com fenômenos. Aliás, julgo que é justamente o foco na fenomenologia o principal aspecto que diferencia o Volume 3 (Mecânica Quântica) das abordagens tradicionais. Muitas destas iniciam o estudo da teoria quântica de maneira bastante abstrata, definindo vetores de estado em um espaço de Hilbert e operações entre eles. Basta uma olhada rápida no índice do Volume 3 para perceber que se trata de uma abordagem bastante diferente, recheada de fenomenologia (Espalhamento em um cristal (3-3), Hélio líquido (4-6), Maser de amônia (Cap. 10), entre outros). De fato, os vetores de estado são apresentados somente no Capítulo 8, quando o estudante já construiu uma intuição sobre a maneira quântica de pensar. Antes disso, muitos fenômenos são discutidos para que a expressão adquira gradativamente um significado físico.
-
Ordem e títulos dos capítulos
Índices de livros-texto de Física tendem a ser muito semelhantes, mas uma breve olhada nos índices das lectures revela algumas diferenças marcantes. Além de alguns títulos tradicionais como “Leis de Newton”, “Eletrostática” ou “Leis da Termodinâmica”, encontramos também outros um tanto inusitados como “Catraca e Lingüeta”, “Análogos Eletrostáticos”, “O Escoamento da Água Seca”, “Mecanismos da Visão” ou “Simetrias nas Leis da Física”. Esse relativo desprendimento indica que o importante é aprender a maneira física de pensar e não necessariamente este ou aquele conteúdo. Além disso, a ordem em que os temas aparecem também se distingue, por exemplo, “Comportamento Quântico” é um capítulo do Volume 1 e “Elasticidade” aparece no final do Volume 2. Em geral, a divisão proposta por Feynman transmite uma imagem mais coerente e interligada da Física, possivelmente contornando o conhecido problema de desmotivação de estudantes que ingressam na universidade e se deparam, nos dois primeiros anos, com reformulações de conteúdos que aprenderam no Ensino Médio.
-
Capítulos de matemática
Outro aspecto que chama a atenção nos índices é a presença de alguns capítulos de matemática (por exemplo, “Probabilidade”, “Vetores”, “Álgebra” ou “Cálculo Integral Vetorial”), os quais normalmente não aparecem em índices de livros-texto de física ou, quando aparecem, são relegados a apêndices. Isso indica que esses tópicos de matemática são tratados como parte integrante da física e rompe com a ideia de matemática como mera ferramenta. Como discutiremos em detalhe na Seção III, Feynman tem uma concepção muito peculiar da relação entre matemática e física e essa é uma importante razão para o sucesso das lectures. Quando reparamos na forma como a matemática é tratada em seu discurso didático, percebemos que se trata de uma matemática diferente da dos livros de matemática, pensada exclusivamente a partir de fenômenos físicos e a serviço da física.
-
Diálogo pessoal
Ao ler um parágrafo das lectures ao acaso normalmente já é possível notar um estilo de discurso bastante diferente dos livros tradicionais. Enquanto estes abordam os conteúdos de maneira mais impessoal e distanciada, a leitura do texto do Feynman se assemelha a um diálogo “de pai para filho(a)”. Não se trata unicamente de alguém que lhe mostra o que é a física e como ela deve ser feita, mas alguém que dialoga contigo, entende profundamente suas angústias, prevê suas dificuldades, mostra limitações da teoria, tem senso de humor, expressa emoções, etc. Esse estilo não só torna a leitura muito mais agradável, mas rompe com o ar de autoridade das apresentações tradicionais proporcionando uma concepção muito mais humana e acessível da física.
3. Relação entre matemática e física
3.1. Matemática como pré-requisito
A noção de matemática como pré-requisito para o aprendizado da física é amplamente encontrada em diversos contextos educacionais, por exemplo, quando cursos de matemática (Cálculo, Álgebra Linear, etc.) são exigidos de estudantes universitários para que os mesmos possam cursar disciplinas de física. Trata-se de uma concepção de matemática como ferramenta para a física que, implicitamente, transmite a ideia de que primeiro as estruturas matemáticas são desenvolvidas para depois serem aplicadas na física.
Feynman evita a noção de matemática como pré-requisito para a física sempre que possível. Inúmeras vezes a estrutura matemática emerge de uma situação física e o conceito matemático formal é apresentado no fim. Além disso, trata-se de uma matemática a serviço da física, em geral muito diferente da encontrada em livros de matemática. Vejamos alguns exemplos.
Velocidade e derivada
Alguns manuais didáticos partem do pressuposto de que o aluno deve saber o que é uma derivada para entender o que é velocidade. Seguindo uma linha mais coerente com o desenvolvimento histórico, Feynman (Cap. 8, Vol. 1) faz exatamente o oposto; ele inicia com uma discussão conceitual muito rica sobre o significado de velocidade a partir da qual o conceito formal de derivada emerge naturalmente.
A discussão se baseia na inusitada situação em que uma senhora é parada por um policial que a alerta dizendo que ela “estava andandando a 100 quilômetros por hora”. A senhora protesta: “Mas senhor, eu saí de casa há 7 minutos!” Na sequência, Feynman nos convida a pensar, de maneira honesta, sobre o que queremos dizer com a asserção “estou me deslocando [neste instante] a 100 quilômetros por hora.”, evidenciando que falar em uma taxa [instantânea!] de variação é algo extremamente contra-intuitivo. Ao tentar expressar essa noção mais precisamente, Feynman aborda a necessidade de se considerar um intervalo de tempo muito pequeno o que nos leva, naturalmente, à ideia de limite e à definição formal de derivada. Dessa forma, todos os termos presentes na definição possuem significado físico. A mensagem central é a seguinte: retiramos a ideia de velocidade do mundo físico e inventamos uma maneira matemática (derivada) para representá-la.
Torque e produto vetorial
É necessário saber o que é o produto vetorial entre dois vetores para que possamos aprender o conceito físico de torque? Novamente a resposta de Feynman é veementemente negativa. Considerações físicas sobre o ato de girar um corpo rígido nos levam naturalmente ao conceito matemático de produto vetorial, primeiramente em duas (18-2, Vol. 1) e depois em três dimensões (20-1, Vol. 1), quando a definição formal de torque é apresentada.
A partir de argumentos cinemáticos, Feynman analisa a essência da rotação em duas dimensões e relaciona, para um sistema de coordenadas cartesianas, o deslocamento em uma componente com a coordenada da outra (Fig. 1).
Em seguida, considerando que haja uma força aplicada, o trabalho realizado pela mesma () é expresso, utilizando as relações cinemáticas obtidas anteriormente, da seguinte forma
o que naturalmente leva a uma discussão sobre o significado da expressão dentro dos parênteses. Partindo de uma analogia entre translação e rotação, o conceito de torque é introduzido, em estreita relação com o conceito de trabalho.
Para generalizar o resultado em três dimensões (20-1, Vol. 1) Feynman utiliza um argumento de simetria para dizer que obteríamos os seguintes torques se tratássemos a situação bidimensional relativa a outros planos ( e )
Em seguida, a questão que se coloca é se as componentes ( e ) formam ou não um vetor. Retomando uma discussão conceitual sobre simetrias feita no Capítulo 11, Feynman mostra que as componentes satisfazem sim certas condições (simetria por rotações dos eixos), logo podem ser consideradas como as componentes de um vetor. Só então o produto vetorial entre dois vetores é apresentado. Assim como no caso da derivada, o produto vetorial emerge de considerações físicas. A diferença entre sua abordagem é nítida quando a comparamos com textos que definem primeiramente o que é um produto vetorial para depois definir torque como . Em suma, para Feynman a física vem primeiro.
3.2. Matematização
Mas é claro que nem sempre é possível fazer a matemática emergir naturalmente da física, aliás em muitos casos isso seria artificial. Usualmente, físicos(as) olham para a matemática como uma caixa de ferramentas e escolhem as estruturas que são mais apropriadas para a descrição das propriedades físicas que desejam representar. Chamamos esse processo de matematização.
Feynman tem uma maneira peculiarmente didática de matematizar. Além de realizada de maneira gradual, a matematização de Feynman é sempre acompanhada de uma discussão explícita das razões pelas quais um determinado formalismo matemático é útil para a situação física em questão. Com frequência, diferentes formalismos e representações são apresentados e uma análise sobre “prós e contras” é conduzida, como ilustramos no exemplo a seguir.
A matemática da interferência
Na Seção 29-5 Vol. 1, Feynman matematiza a interferência, ou seja, discute como tratar de maneira quantitativa a soma de duas ondas (cos)senoidais de mesma frequência, mas que estejam fora de fase, representada por
Três maneiras distintas são apresentadas e num primeiro momento as mesmas parecem igualmente válidas. Restringindo-se ao caso em que as amplitudes são iguais, a primeira é a trigonométrica, e consiste em transformar a soma em um produto utilizando a seguinte identidade trigonométrica
o que permite, comparando (4) e (5), a obtenção da seguinte expressão
Assim, fica evidente que a resultante é uma nova onda cos(senoidal), cuja amplitude e fase são funções das amplitudes e fases das duas ondas que a originaram.
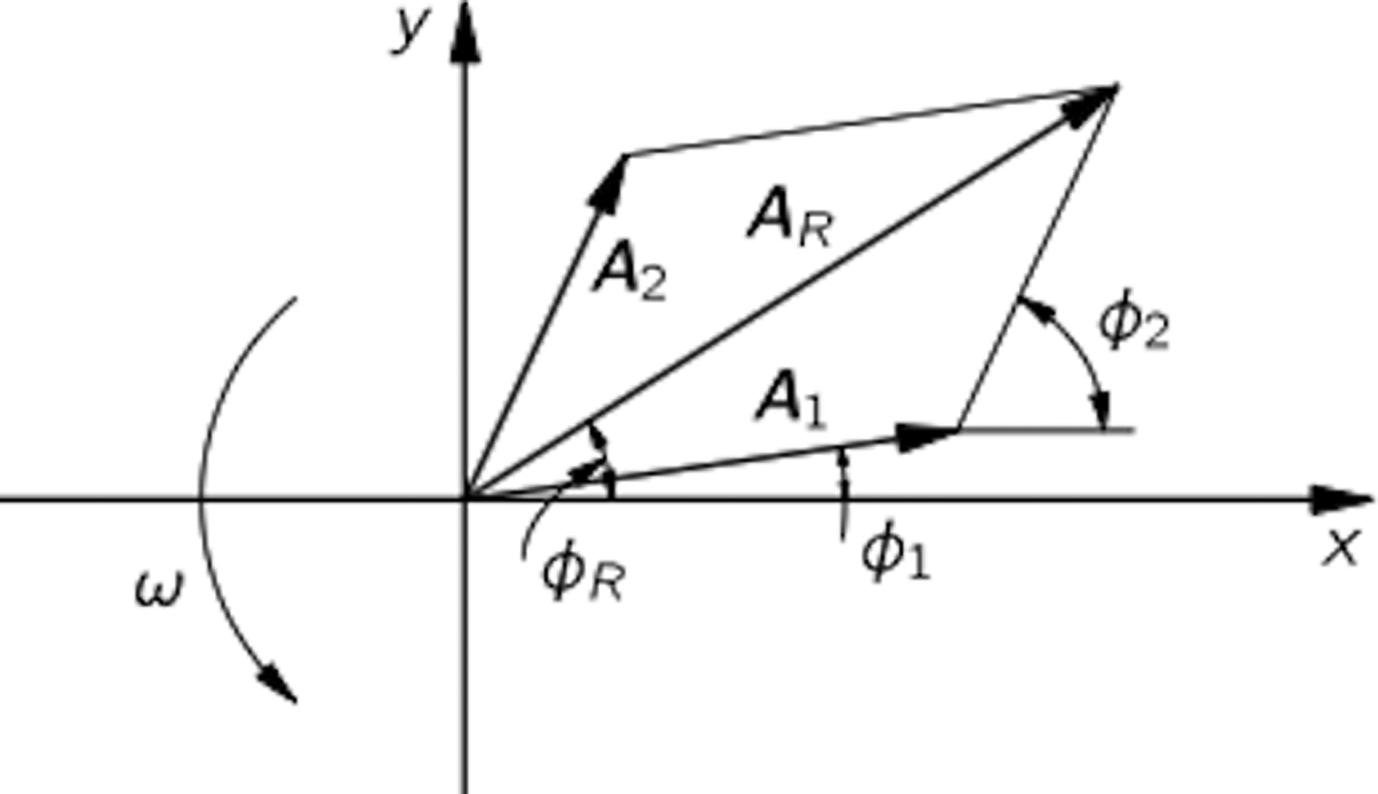
O segundo método é o geométrico e está representado na Figura 2. Este método nos permite determinar a amplitude e a fase da onda resultante a partir de relações geométricas. Além disso, não precisamos nos restringir ao caso de amplitudes constantes.
O terceiro método é o analítico. Ele consiste em utilizar a exponencial complexa (fórmula de Euler) e tratar a parte real como representando a amplitude. Este método é mais vantajoso para fins de cálculo, uma vez que é mais fácil somar e multiplicar expressões que contêm expoentes de mesma base.
Isso significa que devemos optar por um método em detrimento dos outros? Certamente não. Julgo que Feynman apresenta essa diversidade para ampliar nosso conjunto de representações do fenômeno. A mensagem implícita é que um profundo entendimento da matemática da interferência está intimamente relacionado com a habilidade de transitarmos entre essas diferentes representações. Nesse sentido, quanto mais amplo o arsenal, melhor.
3.3. Interpretação
Depois que uma derterminada expressão matemática é derivada, Feynman quase sempre explora o significado físico da mesma, com frequência utilizando casos limite ( ou ) ou particularmente relevantes. Trata-se do caminho inverso da matematização, ou seja, buscar interpretações físicas no formalismo matemático. Isso se reflete em perguntas do tipo “O que significa que a expressão depende dessa variável dessa maneira?”, “O que acontece com quando tende a zero/infinito?”. Esse tipo de discurso ocorre o tempo todo, com muito mais frequência e intensidade que nos livros tradicionais. Ilustremos com um exemplo (existem muitos outros).
Índice de refração é um número complexo
No Capítulo 31 do Volume 1, uma verdadeira obra-prima, encontramos uma análise detalhada da origem do índice de refração, a partir de considerações sobre campos elétricos gerados pelo movimento de cargas elétricas que compõem uma placa de vidro. Temos a sensação de penetrar (com a mente) na estrutura da matéria para calcular o campo elétrico resultante em um ponto , à direita da placa. Assumindo que os elétrons se comportam como osciladores sujeitos a uma força linear restauradora, a seguinte expressão é obtida para o índice de refração
onde é o número de elétrons por unidade de volume na placa, a frequência da radiação e a frequência ressonante de um elétron.
Na sequência (Seção 31-3), duas páginas de texto corrido são dedicadas a uma detalhada interpretação do significado da equação (8), bem como suas aplicações e limitações, um exemplo claro de como o discurso de Feynman se distingue dos livros tradicionais. No final desta seção, o modelo utilizado para os elétrons é modificado, adicionando-se uma força de amortecimento e considerando que existem tipos diferentes de osciladores, com diferentes frequências ressonantes . Com essas duas alterações a nova expressão para o índice de refração é
Existe uma diferença importante entre as equações (8) e (9), e Feynman prontamente chama nossa atenção:
Talvez você tenha notado algo um pouco estranho sobre a última fórmula [Eq. 9] que obtivemos para a nossa equação de dispersão. Por termos introduzido o termo para considerar o amortecimento, o índice da refração é agora um número complexo! O que significa isso? (31-4, Vol. 1, itálicos no original)
O que segue é uma brilhante explicação do porquê a parte complexa do índice de refração pode ser interpretada como coeficiente de absorção. Ou seja, a física é extraída do formalismo matemático. É incrível!
3.4. (De)mostrando equações
Alguns clássicos da física se parecem com os de matemática, uma vez que apresentam proposições que são demonstradas a partir de princípios gerais e raciocínio lógico. Basta folhear os Principia do Newton e os Elementos de Euclides para notar tal semelhança. Em um comentário de natureza epistemológica (ver Seção IV), Feynman expressa essa característica da física da seguinte forma:
[...] para o desenvolvimento adicional da ciência, queremos mais do que apenas uma fórmula. Primeiramente, temos uma observação, então temos os números que medimos, e depois temos uma lei que resume todos os números. Mas a real glória (beleza) da ciência é que podemos descobrir uma maneira de pensar tal que a lei é evidente. (26-3, Vol. 1)
Livros-texto de física estão repletos de demonstrações e isso não é diferente nas Feynman lectures. Porém, o diferencial destas é que muitas vezes encontramos maneiras originais e argumentos incomuns para demonstrar tais conexões. Em geral, o raciocínio físico vem em primeiro lugar e o “rigor matemático” fica em segundo plano. Isso torna as demonstrações mais acessíveis e significativas. Vejamos alguns exemplos:
Lei de Snell a partir do princípio de Fermat
Toda óptica geométrica pode ser deduzida a partir de um único princípio: a luz se desloca de até pelo caminho de menor tempo. Eis como Feynman usa esse princípio para demonstrar a lei de Snell da refração.
Na Figura 3 a trajetória da luz para ir do ponto ao ponto é representada por . Segundo o princípio de Fermat, esse é o caminho que leva o menor tempo. Isso significa que se pensarmos no tempo para ir de até como uma função da posição do ponto em que a luz muda de meio, a trajetória representa um extremo (mínimo). A ideia central do cálculo de variações é a seguinte: um pequeno (infinitesimal) deslocamento a partir de um extremo não altera seu valor.
Na Figura 3 esse deslocamento infinitesimal é representado pelo ponto . Agora, a luz percorre uma outra trajetória, . Porém, como está infinitamente próximo de , pode-se dizer que a luz percorre o trajeto no mesmo tempo que em . Como expressar isso matematicamente? Basta perceber que para a trajetória a luz percorre uma distância maior no ar (). Por outro lado, para a trajetória a luz percorre uma distância maior na água (). Como está infinitamente próximo de e é um extremo, o tempo que a luz leva para percorrer no ar tem que ser igual ao tempo que a luz leva para percorrer na água. Representando essa igualdade matematicamente, obtemos a lei de Snell:
Desconheço uma maneira mais simples de demonstrar a lei da refração. E a beleza dessa demonstração não está somente em sua simplicidade, mas principalmente porque ela nos mostra uma conexão profunda e inesperada entre uma lei “fenomenológica” da luz e um princípio geral com ares de divindade.
A atmosfera exponencial e a lei de Boltzmann
A lei (distribuição) de Boltzmann é um dos grandes pilares da mecânica estatística. Maneiras tradicionais de demonstrá-la são baseadas no conceito de entropia e fazem uso de argumentos probabilísticos. Feynman nos apresenta uma forma bastante diferente e inusitada de obter tal lei.
A demonstração baseia-se na ideia de uma atmosfera exponencial. Uma coluna de ar (gás ideal) em um campo gravitacional é mantida a uma temperatura constante (Fig. 4). Considerando uma camada de espessura e seção unitária, a diferença de pressão entre as partes inferior e superior deve ser responsável pelo equilíbrio da mesma, o que pode ser expresso por , onde expressa o número de moléculas por unidade de volume.
Como , e é constante, podemos eliminar e substituí-lo por , obtendo a seguinte equação diferencial
cuja solução é
Em seguida, Feynman nos chama a atenção para o fato de que a expressão no expoente é energia potencial de um átomo. Seria uma mera coincidência? Ao generalizar o exemplo para uma força definida a partir de um potencial, Feynman mostra que não, e expressa a lei de Boltzmann da seguinte forma
onde E.P. é a energia potencial. Para quem já viu maneiras tradicionais de se obter a distribuição de Boltzmann, essa “demonstração” parece mágica. Certamente, ela amplia o conjunto de relações que estabelecemos quando pensamos na lei de Boltzmann.
Mas qual é o papel de demonstrações no ensino de física? Será que os estudantes devem memorizá-las e reproduzi-las em avaliações? Eis o que Feynman, em seu estilo metacognitivo (Seção IV), diz a respeito:
Ao aprender qualquer assunto de uma natureza técnica onde a matemática tem o seu papel, uma pessoa é confrontada com a tarefa de entender e guardar na memória um grande número de fatos e ideias, mantidos juntos por certas relações existentes entre elas que podem ser “demonstradas” ou “mostradas”. É fácil confundir a demonstração em si com a relação que ela estabelece. Claramente, a coisa importante a aprender e a lembrar é a relação, não a demonstração. Em qualquer circunstância em particular podemos dizer “pode ser mostrado que” tal e tal são verdadeiros ou podemos mostrá-los. Em quase todos os casos, a particular demonstração que é usada, é planejada, primeiro de tudo, de tal forma que pode ser escrita rapidamente e facilmente em um quadro negro ou em um papel para ter a aparência mais agradável possível. Consequentemente, a demonstração pode parecer enganosamente simples, quando de fato, o autor pode ter trabalhado por horas tentando diferentes maneiras de calcular a mesma coisa até que ele achou a maneira mais concisa, assim fica possível mostrar que a demonstração pode ser feita em pouco tempo! A coisa a se lembrar, quando vemos uma demonstração, não é a demonstração propriamente dita, mas que pode-se mostrar que tal e tal coisa são verdadeiras. Obviamente, se a demonstração envolve alguns procedimentos matemáticos ou “truques” que as pessoas não viram antes, a atenção deve ser dada não ao truque exatamente, mas a ideia matemática envolvida (14-1, Vol. 1).
Esta longa citação tem um valor pedagógico enorme. Ela explicita ao estudante o que é importante compreender quando se acompanha uma demonstração e deixa claro que há um esforço gigante de quem as desenvolveu para apresentá-la de maneira concisa. Livros tradicionais costumam ser silenciosos neste aspecto e, implicitamente, transmitem a ideia de que tais demonstrações são realmente triviais, frustrando a grande maioria dos estudantes que não as acompanha.
3.5. Analogias
O extensivo uso de analogias na física se deve à busca incessante por conexões profundas, as quais nem sempre são notáveis diante da (aparente) diversidade de fenômenos que observamos. Assim, um dos objetivos dessa ciência é explicar o maior número de fenômenos possível com o menor número de conceitos e princípios. As grandes unificações da história da física (eletromagnetismo e ótica, teoria cinética dos gases, etc.) e alguns dos maiores desafios atuais (unificação da mecânica quântica com a relatividade geral) são exemplos dessa prática. Trata-se de uma questão estética, uma busca por unicidade/simplicidade teórica. Do ponto de vista didático, utilizar analogias também pode estar associado à ideia de construir um novo conhecimento a partir daquilo que o aluno já sabe.
As Feynman lectures são repletas de analogias. Mais uma vez o leitor pode protestar dizendo que todos os livros de física possuem analogias. Novamente, acredito que tanto a quantidade como a qualidade das analogias que encontramos nas lectures as distinguem dos livros tradicionais. Por exemplo, já no Capítulo 4 do Volume 1, nos deparamos tanto com a genial analogia entre a ideia de conservação de energia e a situação do menino com 28 blocos, como, logo em seguida, com a descrição de uma inusitada máquina reversível (mecânica, não térmica) que introduz a noção de energia potencial gravitacional. No Volume 2 (Eletromagnetismo), não só muitas noções básicas de cálculo vetorial (como gradiente e divergente) são apresentadas em um contexto de condução do calor, como encontramos um capítulo inteiro, chamado Análogos Eletrostáticos (Cap. 12, Vol. 2), no qual fenômenos bastante distintos são expressos com o formalismo da eletrostática. No final do capítulo (12-7), Feynman discute profundamente se é ou não razoável supor que exista uma “unidade subjacente” na natureza.
Além da tentativa de explicar fenômenos diversos com o mesmo formalismo, algumas vezes Feynman nos surpreende ao evidenciar semelhanças entre formalismos matemáticos aparentemente distintos. A seguir apresentamos dois exemplos.
Operações diferenciais com o Nabla
Qual o divergente do rotacional de um campo vetorial? E o rotacional do gradiente de um certo campo escalar? Estudantes de física cursando eletromagnetismo utilizam essas operações para manipular as equações de Maxwell e estão acostumados a determiná-las a partir das definições de cada um dos operadores diferenciais. Mas Feynman quer que tenhamos uma certa intuição sobre elas e, para isso, faz uso de analogias com operações já conhecidas entre vetores (Seção 2-7, Vol. 2).
Dados três vetores A, B e C, um escalar e os conhecidos produtos escalar e vetorial, é possível concluir que
Tratando o símbolo Nabla () como uma espécie de vetor, concluímos, por analogia com as equações (14), que para um campo escalar e um vetorial h são válidas as seguintes relações
Simples assim. Esse é um bom exemplo da maneira peculiar, e muitas vezes não rigorosa, que Feynman tem de lidar com a matemática e sua capacidade de nos mostrar conexões inesperadas entre tópicos aparentemente novos e difíceis, e assuntos que julgamos antigos e triviais.
Produto escalar e o formalismo da mecânica quântica
Conforme já mencionamos, Feynman só introduz o conceito de vetores de estado na mecânica quântica no Capítulo 8 do Volume 3. E ele o faz por meio de uma analogia. Vejamos como.
Nos capítulos 5 e 6, Feynman discute diversas situações envolvendo experimentos com átomos filtrados usando aparatos do tipo Stern-Gerlach. Um dos objetivos destes capítulos é introduzir a noção de estados de base, e representar a amplitude de se começar em um estado e terminar em da seguinte forma
onde são estados de base descritos e exemplificados em capítulos anteriores.
Em seguida Feynman nos mostra uma semelhança entre a equação (16) e o produto escalar entre dois vetores A e B, escrevendo este como
onde são os conhecidos vetores unitários nas direções , e para o caso de três dimensões. Assim, representa a projeção do vetor na direção de , isto é, sua componente nesta direção. Por exemplo, , e assim por diante. Logo, percebemos que a equação (17) nada mais é do que a conhecida
A partir da semelhança formal entre as equações (16) e (17), Feynman cogita a possibilidade de se representar um estado por um vetor e interpretar a amplitude como uma espécie de produto escalar entre os vetores que representam os estados inicial e final. Em seguida, ele discute cuidadosamente algumas diferenças importantes, por exemplo, a não comutatividade do produto escalar na mecânica quântica. Pela primeira vez os elementos da notação de Dirac (bra-ket) são tratados separadamente. Vemos mais um exemplo no qual o formalismo vai sendo construído, gradualmente, em vez de ser imposto. É simplesmente genial.
4. Epistemologia e metacognição
A última seção é dedicada a um aspecto que possivelmente é o grande diferencial das lectures. Trata-se da habilidade ímpar que Feynman possui de refletir sobre a natureza do conhecimento físico e sobre os desafios inerentes a sua aprendizagem. Assim, seu discurso didático é extremamente metacognitivo e filosófico, muito diferente dos livros tradicionais. Vamos discutir estes aspectos (epistemologia e metacognição) separadamente, apesar de muitas vezes eles estarem intimamente ligados.
4.1. Epistemologia
Feynman não só ensina física, mas ensina muito sobre o que é fazer física e sobre a natureza do conhecimento físico. Logo, seu discurso é extremamente epistemológico. Livros tradicionais tendem a ser silenciosos no que diz respeito a questões epistemológicas, com frequência dedicam tais discussões para um capítulo inicial, por exemplo, abordando o “método científico”, uso de modelos, etc. Feynman discute epistemologia em praticamente todos os capítulos das lectures e o faz de maneira estreitamente ligada com o conhecimento específico que está tratando, o que torna a discussão muito mais rica. A seguir apresento alguns exemplos, existem muitos outros.
Isso parece ser apenas uma definição, e é notável que possamos transformar leis físicas em meras definições. (10-2, Vol. 1)
Todas as nossas idéias em física exigem uma certa dose de senso comum em sua aplicação; elas não são idéias puramente matemáticas ou abstratas (11-1, Vol. 1)
Podemos sentar em uma poltrona o dia todo e definir palavras ao nosso bel-prazer, mas descobrir o que acontece quando duas bolas colidem uma contra outra, ou quando um peso é pendurado em uma mola, é completamente diferente, porque o modo como os corpos se comportam é algo completamente fora de qualquer grupo de definições. (12-1, Vol. 1)
Alguém pode ficar insatisfeito com a visão aproximada da natureza que a física tenta obter (a tentativa é sempre aumentar a precisão da aproximação), e pode preferir uma definição matemática; mas definições matemáticas nunca podem funcionar no mundo real. (12-2, Vol. 1)
Já fizemos alguns comentários sobre a indeterminação da mecânica quântica. Ou seja, que somos incapazes de prever o que vai acontecer em física numa dada circunstância arranjada tão cuidadosamente quanto possível. Se temos um átomo que está num estado excitado e portanto vai emitir um fóton, não podemos dizer quando ele vai emitir o fóton. Existe uma certa amplitude de emitir o fóton em qualquer instante e podemos apenas prever a probabilidade de emissão; não podemos prever o futuro exatamente. Isso originou todo tipo de questões sem sentido sobre desejos e liberdade e a noção de que o mundo seja incerto. (2-9, Vol. 3)
4.2. Metacognição
Metacognição tem a ver com o conhecimento sobre nossos próprios processos cognitivos e a habilidade que temos de os monitorar. Nesse sentido, o texto de Feynman é extremamente metacognitivo, pois é repleto de tais reflexões. O tempo todo, sentimos que estamos sendo guiados por uma pessoa muito clara e honesta. Somos constantemente informados sobre por que estamos procedendo dessa forma, quais as limitações, que dificuldades existem para entendermos o conteúdo, o que é essencial entender, o que nos falta, onde estamos, para onde vamos, etc. Isso torna a leitura muito mais agradável e nossa relação com a física muito mais humana. As citações a seguir ilustram esse caráter metacognitivo do discurso de Feynman.
Esta discussão sobre vetores pode não estar completa. Entretanto, em vez de tentar aprofundar o tema agora, vamos primeiro aprender a usar, em situações físicas, algumas das idéias discutidas até então. Então, quando tivermos dominado apropriadamente este material básico, vamos achar mais fácil penetrar mais profundamente no assunto sem ficarmos muito confusos. (11-11, Vol. 1)
Uma das razões do porque faremos essa análise tão imperfeitamente é que a matemática necessária requer uma compreensão profunda da teoria de probabilidades; não queremos saber onde cada átomo está de fato se movendo, mas antes quantos se movem aqui e lá em média, e qual a probabilidade de diferentes efeitos. Portanto esse assunto implica um conhecimento da teoria de probabilidade, e a nossa matemática ainda não está razoavelmente pronta e não queremos forçá-la muito. (39-1, Vol. 1)
Provavelmente, isso é a coisa mais complicada que iremos fazer neste ano, mas é complicado porque há muitas partes que têm que ser unidas; cada parte, contudo, é muito simples. (31-1, Vol. 1)
Levará algum tempo até você entender o que pode acontecer em diferentes circunstâncias. Você terá de resolver as equações. Cada vez que resolver as equações, aprenderá algo sobre o caráter das soluções. Para ter em mente estas soluções, é útil também estudar seu significado em termos de linhas de campo e outros conceitos. Desta forma, você realmente “entenderá” as equações. Esta é a diferença entre a matemática e a física. Matemáticos, ou pessoas que possuem uma mente muito matemática, geralmente se desencaminham quando “estudam” física, porque perdem o aspecto físico. Eles dizem: “veja, estas equações diferenciais â– as equações de Maxwell â– são tudo que existe na eletrodinâmica; os físicos admitem que não há nada que não esteja contido nestas equações. Estas equações são complicadas, mas são apenas equações matemáticas e, se eu entendê-las matematicamente em profundidade, entenderei a física em profundidade”. Todavia, as coisas não funcionam assim. Matemáticos que estudam física com este ponto de vista â– e há muitos deles â– normalmente, fazem poucas contribuições à física e, na verdade, poucas para a matemática. Eles falham porque as situações físicas no mundo real são tão complicadas que é necessário ter um conhecimento mais amplo das equações. (2-1, Vol. 2)
Outra evidência do caráter metacognitivo de Feynman é que com frequência ele parece antecipar nossas perguntas. Em diversos momentos ele questiona o leitor “mas agora você deve estar pensando:”, e muitas vezes ele acerta nos deixando intrigados: “Mas era exatamente isso que eu estava pensando! Como é que ele sabe?”. Isso revela um profundo conhecimento de Feynman sobre raciocínios plausíveis (mesmo que não corretos cientificamente) e uma sensibilidade de levá-los em conta no ensino. Vejamos alguns exemplos:
Agora você diz: “Mas com quais eixos?” Isto não depende dos eixos, a resposta é a mesma para qualquer conjunto de eixos. (11-7, Vol. 1)
Obviamente podemos pensar se essa curva é muito simples. E se usássemos uma curva real? (13-5, Vol. 1)
Então, a força é independente da distância a! Por quê? Fizemos um erro? Alguém pode pensar que quanto mais distante formos, mais fraca a força deveria ser. Mas não! (13-8, Vol. 1)
Mas, para um pedaço de vidro, você poderia pensar: “Oh, não, você deve modificar tudo isso. Você deveria dizer que o atraso da velocidade é ”. Isso porém não é correto, e temos que entender o porquê. (31-1, Vol. 1)
Você pode estar dizendo: “todo este negócio de fluxos e circulações é bastante abstrato. Os campos elétricos estão em todos os pontos do espaço; então surgem estas “leis”. Mas o que está acontecendo realmente? Por que isto não pode ser explicado, por exemplo, pelo que quer que esteja acontecendo entre as cargas?” Bem, isto depende de seus preconceitos. (1-5, Vol. 2)
Eu pedi para você imaginar estes campos elétricos e magnéticos. O que você faz? Você sabe como fazer? Como é que eu imagino os campos elétricos e magnéticos? O que eu vejo de verdade? Quais são as pretensões da imaginação científica? Existe alguma diferença entre fazer isto e tentar imaginar que a sala está repleta de anjos invisíveis?
É necessário um grau muito maior de imaginação para entender os campos eletromagnéticos do que para entender anjos invisíveis. [...] Então você diz, “professor, por favor dê uma descrição aproximada das ondas eletromagnéticas, mesmo que ela seja ligeiramente incorreta, de modo que eu também possa vê-las tão bem como eu posso ver anjos quase invisíveis. Então eu posso modificar a figura com a abstração necessária.”
Sinto muito, mas não posso fazer isto para você. Eu não sei como fazer isto. Eu não tenho uma imagem do campo eletromagnético que seja correta de alguma maneira. (20-3, Vol. 2)
Esta última citação é uma de minhas favoritas (Qual é a sua?). Ela é de uma honestidade incrível e nos transmite uma sensação de tranquilidade, uma vez que não só percebemos que é natural procurar imagens e explicações mecanicistas para a propagação de ondas eletromagnéticas no espaço, mas também que muitas vezes em física somos obrigados a abrir mão de certos modelos e imagens próximos de nossa realidade imediata.
5. Considerações finais
-
Princípios didáticos gerais
Iniciamos este artigo anunciando o objetivo de deduzir alguns princípios didáticos das Feynman lectures. Os dez itens a seguir são uma tentativa inicial nessa direção. Sem nenhuma pretensão de ser exaustiva, a lista foi formulada em estilo prescritivo somente com o intuito de ser mais objetiva.
-
Melhor resolver 1 problema de 4 maneiras diferentes do que 4 problemas da mesma maneira;
-
Parta do simples ao complexo; do concreto ao abstrato;
-
Quando possível, faça a matemática emergir de situações físicas;
-
Evite ao máximo argumentos autoritários como “esse é um teorema matemático”; Seja criativo, reinvente teoremas, faça suas próprias demonstrações;
-
Seja honesto com o estudante, reflita sobre as dificuldades para se entender o conteúdo e explicite-as quando for ensinar;
-
Procure evidenciar conexões e analogias profundas entre assuntos aparentemente distintos;
-
O conhecimento físico não é dividido em caixas, mostre relações entre as áreas da física;
-
Preencha de fenomenologia todo e qualquer assunto que for ensinar;
-
Não ensine somente física, mas também o que significa fazer física;
-
Seja metacognitivo em seu discurso; Explicite onde você está, onde quer chegar, como pretende chegar lá, quais são as possíveis armadilhas, etc.
-
Feynman lectures como livro-texto?
Uma questão que se coloca com frequência em debates acerca das lectures é se as mesmas devem ou não ser utilizadas como livro-texto em cursos introdutórios de física. Muitos defendem prontamente que não, argumentando que as lectures são ideais para quem já tem um sólido conhecimento de física e deseja entender as coisas de outra maneira, mas que não são adequadas para iniciantes. Com frequência, o argumento é baseado no “fato” de que, com o passar do tempo, os estudantes de níveis iniciais foram deixando de frequentar as lectures e foram sendo substuídos por alunos de pós-graduação e membros do corpo docente da Caltech. Trata-se de uma lenda apresentada por Goodstein [5][5] D. L. Goodstein, Physics Today 42, 70 (1989). e veementemente refutada por Sands [3][3] M. Sands, Physics Today 58, 49 (2005)..
De qualquer forma, julgo que o debate sobre as adotar ou não como livro-texto não é muito produtivo. Como procuramos evidenciar neste artigo, a comparação das Feynman lectures com livros-texto tradicionais nos mostra que se tratam de propostas didáticas com objetivos bastante distintos. Assim, antes de decidir que material utilizar em um determinado curso, é preciso discutir e definir seus objetivos formativos. É nesse contexto que Goodstein avalia o sucesso das lectures ([5][5] D. L. Goodstein, Physics Today 42, 70 (1989)., p. 70):
Se seu propósito em ministrar as lectures foi preparar seus alunos para resolver problemas cobrados em exames, ele provavelmente não foi muito bem sucedido [...] Se, entretanto, seu objetivo foi ilustrar, de maneira exemplar, como pensar e raciocinar em física, então, em todas indicações, ele foi brilhante.
É claro que é ingênuo e simplista pensar que haja uma dicotomia entre compreensão conceitual e resolução de problemas, é mais do que sabido que ambos estão intimamente relacionados. Porém, é preciso distinguir os meios dos fins. Acredito que para a maioria dos livros tradicionais, a resolução de problemas é um fim, enquanto que para Feynman, ela é um meio.
Talvez o maior desafio em adotar a proposta de Feynman, a qual prioriza uma profunda compreensão conceitual e está repleta de discussões epistemológicas, seja lidar com as ansiedades inerentes ao risco de sairmos de nossa zona de conforto. Sabemos muito bem seguir um modelo de ensino que consiste em treinar alunos para resolver problemas que serão cobrados em exames, fomos formados nessa tradição. Muito mais difícil é pensar que tipo de contrato didático estabelecer e como avaliar os objetivos didáticos da proposta de Feynman.
-
O que motivou Feynman a preparar e ministrar as lectures?
Outra questão interessante é a seguinte: Por que Richard Feynman, que no início da década de 60 já era um físico consagrado internacionalmente, resolveu dedicar tanto tempo e esforço ao desenvolvimento de cursos para o nível introdutório? Existem várias explicações possíveis, entre elas a vaidade (Feynman adorava um palco). Mas, como o próprio Feynman nos revela, a razão principal é que conseguir explicar de forma compreensível a alunos de cursos introdutórios de física era seu principal indicador de que ele realmente entendeu algo. Sendo assim, talvez o próprio Feynman seja quem tenha mais aprendido com suas lectures. Trata-se de um grande incentivo, ou um belo contra-exemplo, para aqueles que veem o ensino como um obstáculo para o desenvolvimento da pesquisa.
-
A importância da obra de Feynman para o ensino de física: Menos metodologia, mais epistemologia
Durante uma de suas visitas ao Brasil, quase dez anos antes de ministrar as famosas lectures, Feynman resumiu sua “filosofia pedagógica” da seguinte forma:
Em primeiro lugar, descubra por que quer que os alunos aprendam o tema e o que quer que saibam, e o método resultará mais ou menos por senso comum.
Claro que nesse caso “senso comum” é relativo. De qualquer forma, o importante é entender o quão fundamental é uma compreensão conceitual profunda da física para pensar seu ensino, algo que tem sido negligenciado em algumas pesquisas da área.
Um estudo que pretende identificar aspectos que caracterizem a qualidade didática das lectures de Feynman não pode ser concluído, mas sim deixado de lado temporariamente devido ao deadline para envio de trabalhos a esta edição especial. Sendo assim, mais do que uma singela homenagem a um ídolo e um dos maiores didatas da física de todos os tempos, este artigo é um convite à comunidade para discutirmos a obra de Feynman de maneira mais sistemática. Podemos fazê-lo de uma forma muito simples: lendo capítulos das lectures e discutindo com nossos alunos, especialmente se forem licenciandos em física. Portanto, permitam-me formalizar este convite parafraseando Laplace: Leiam Feynman, leiam Feynman, ele é o mestre de todos nós!
Agradecimentos
Agradeço ao Nelson Studart pelo convite, incentivo e paciência com os pedidos de extensão de prazo. Além do próprio Nelson, sou grato aos inúmeros colegas com os quais discuti sobre a qualidade das Feynman lectures, entre eles, Fabiana Kneubil, Manoel Robilotta, Carlos Eduardo Aguiar, Ildeu de Castro Moreira, Steen Hansen e Christian Joas; o que não significa, é claro, que eles concordariam com tudo que está escrito no artigo. Por fim, agradeço ao Michael Gottlieb e à editora Hachette Book Group pela permissão para reproduzir as figuras originais, todas retiradas da versão gratuita online disponível em www.feynmanlectures.caltech.edu.
-
1
Por “tradicionais” entendemos clássicos como Halliday, Resnick e Walker; Tipler e Mosca; Sears e Zemansky; Young e Freedman; e similares. Usualmente, tais livros são destinados a um público bastante abrangente (inclusive engenheiros) e são muito semelhantes em sua forma e conteúdo.
-
2
Isso tem sido motivo de críticas à funcionalidade das lectures e é uma possível razão pela qual elas não são comummente adotadas como livro-texto. Buscando responder a tais demandas, alguns volumes com listas de problemas para acompanhar as lectures foram publicados. Uma análise comparativa da natureza desses problemas pode ser outro caminho para indicar diferenças importantes em relação aos livros tradicionais.
Referências
-
[1]R.A.S. Karam, Estruturação matemática do pensamento físico no ensino: uma ferramenta teórica para analisar abordagens didáticas. Tese de Doutorado, Universidade de São Paulo, São Paulo (2012).
-
[2]R.A.S. Karam, Phys. Rev. ST Phys. Educ. Res. 10, 010119 (2014).
-
[3]M. Sands, Physics Today 58, 49 (2005).
-
[4]R.P. Feynman, R.B. Leighton, M. Sands, Lições de física de Feynman: a edição definitiva (Bookman, Porto Alegre, 2008), v. 3, p. 1798.
-
[5]D. L. Goodstein, Physics Today 42, 70 (1989).
Datas de Publicação
-
Publicação nesta coleção
2018
Histórico
-
Recebido
06 Mar 2018 -
Revisado
04 Abr 2018 -
Aceito
05 Abr 2018