Resumos
Neste artigo analisamos as sombras de buracos negros girantes de Kerr e a sua ligação com a primeira imagem de um buraco negro obtida pela colaboração internacional Telescópio Horizonte de Eventos. Obtemos analiticamente a sombra do buraco negro girante de Kerr a partir da forma das órbitas esféricas de fótons. Também utilizamos o método numérico denominado de tracejamento inverso de raios para gerar imagens que ilustram a percepção visual de um observador na presença de um buraco negro girante com e sem um disco de acreção.
Palavras-chave
Relatividade Geral; Buracos Negros Girantes; Sombras de Buracos Negros
In this article we analyze the shadows of spinning Kerr black holes and their connection with the first image of a black hole obtained by the international collaboration Event Horizon Telescope. We obtain analytically the shadow of a rotating black hole from the spherical photon orbits. We also use the method known as backwards ray-tracing to illustrate the visual perception of an observer in the presence of a spinning black hole with and without an accretion disk.
Keywords
General Relativity; Rotating Black Holes; Black Hole Shadows
1. Introdução
Os buracos negros são uma das previsões mais intrigantes da Teoria da Relatividade Geral (TRG). Estes objetos misteriosos são caracterizados por uma superfície de não retorno, denominada horizonte de eventos, de onde nem mesmo a luz consegue escapar.
A forma final das equações de campo da TRG foi proposta no ano de 1915 por Albert Einstein. Estas equações de campo relacionam a curvatura do espaço-tempo com o conteúdo de momento e energia presente no mesmo [11. R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984)., 22. S. Carroll, Spacetime and Geometry (Addison Wesley, San Francisco, 2004)., 33. M.P. Hobson, G.P. Efstathiou e A.N. Lasenby, General Relativity: an Introduction for Physicists (Cambridge University Press, Cambridge, 2006)., 44. R. D’Inverno, Introducing Einstein’s Relativity (Clarendon Press, Oxford, 1992)., 55. C.W. Misner, K.S. Thorne e J.A. Wheeler, Gravitation (Freeman, San Francisco, 1973).]. A relação entre geometria e matéria pode ser sucintamente descrita com a frase atribuída a John Archibald Wheeler [66. J.A. Wheeler e K. Ford, Geons, Black Holes and Quantum Foam: A life in Physics (WW Norton, Nova York, 1998).]: “Spacetime tells matter how to move; matter tells spacetime how to curve”1 1 Uma tradução para o português é: “O espaço-tempo diz à matéria como se mover; a matéria diz ao espaço-tempo como se encurvar”. .
A primeira solução exata para as equações de campo da Relatividade Geral, também conhecidas como equações de Einstein, foi obtida ainda em 1915 por Karl Schwarzschild [77. A. Saa, Rev. Bras. Ensino Fís. 38 , e4201 (2016).]. Esta solução, conhecida simplesmente como solução de Schwarzschild, descreve o espaço-tempo ao redor de um buraco negro sem carga elétrica, com simetria esférica e sem rotação. Logo em seguida, foi obtida uma nova solução de um buraco negro sem rotação e carregado eletricamente, por Hans Jacob Reissner em 1916 e, independentemente, por Gunnar Nordström em 1918 [88. J.P.B. Brito, R.P. Bernar, C.L. Benone e L.C.B. Crispino, Rev. Bras. Ensino Fís. 42, e20200015 (2020).]. Apesar de buracos negros com rotação serem importantes no contexto astrofísico, a primeira solução exata com rotação foi obtida somente em 1963 por Roy Patrick Kerr [99. R.P. Kerr, Phys. Rev. Lett. 11, 237 (1963).]. A métrica de Kerr, como ficou conhecida, constitui a solução paradigmática de referência de um buraco negro da TRG.
Apesar de por vezes serem considerados objetos exóticos pelo público, os buracos negros são na verdade bastante comuns em nosso Universo. Estima-se que no centro da grande maioria das galáxias exista um buraco negro supermassivo, cuja massa possa ser bilhões de vezes maior que a do Sol. Devido à sua enorme massa, alguns destes buracos negros chegam a estar no limiar de nossa capacidade observacional. De fato, recentemente a colaboração internacional Telescópio Horizonte de Eventos (THE) registrou a primeira imagem de um buraco negro, reproduzida na Fig. 1 [1010. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L1 (2019)., 1111. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L2 (2019)., 1212. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L3 (2019)., 1313. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L4 (2019)., 1414. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L5 (2019)., 1515. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L6 (2019).]. Este buraco negro está situado na região central da galáxia Messier 87 (M87), a uma distância de aproximadamente 16.8 mega parsecs de nós (cf. Fig. 2). Ou seja, os raios de luz presentes na imagem do buraco negro foram emitidos cerca de 55 milhões de anos atrás. Este objeto compacto, conhecido como M87*, tem uma massa estimada em aproximadamente 6 bilhões de massas solares.
Resultado apresentado pela colaboração THE como a primeira imagem de um buraco negro. O buraco negro está cercado por matéria difusa, chamada de disco de acreção, que gera uma região luminosa ao redor do buraco negro. Cortesia do Telescópio Horizonte de Eventos (THE) [1616. https://eventhorizontelescope.org.
https://eventhorizontelescope.org... ].
Fotografia da galáxia M87 (no centro da imagem) e galáxias circundantes presentes na constelação de Virgem. Cortesia de Robert Gendler [1717. http://www.robgendlerastropics.com.
http://www.robgendlerastropics.com... ].
Um buraco negro absorve toda a radiação que se aproxima o suficiente do horizonte de eventos, criando uma silhueta escura quando iluminado por um disco de acreção em seu redor. Esta silhueta é a sombra do buraco negro. No contexto da TRG, raios de luz de alta frequência seguem trajetórias especiais, denominadas geodésicas nulas. As curvas geodésicas, e por consequência, as trajetórias de um raio de luz, estão relacionadas com a geometria do espaço-tempo. O campo gravitacional de um objeto massivo encurva a trajetória de um raio de luz, criando um efeito semelhante a uma lente, daí o nome “Lentes Gravitacionais”. O encurvamento de um raio de luz na presença do campo gravitacional do Sol foi medido no ano de 1919, sendo os resultados consistentes com os previstos pela TRG [1818. F.W. Dyson, A.S. Eddington e C. Davidson, Philos. Trans. R. Soc. Lond. A 220, 291 (1920).]. (Ver também as Refs. [1919. L.C.B. Crispino e M.C. Lima, Rev. Bras. Ens. Fís. 38, e4203 (2016).] e [2020. L.C.B. Crispino e D.J. Kennefick, Nat. Phys. 15, 416 (2019).] para um apanhado histórico sobre o assunto e sobre a contribuição das medidas feitas na cidade de Sobral, no Ceará). O ângulo máximo de deflexão medido de um raio de luz foi de aproximadamente 1.75 segundos de arco (as). No entanto, para um buraco negro este ângulo pode ser arbitrariamente grande, pois o campo gravitacional na sua vizinhança pode se tornar tão intenso que mesmo um raio luz pode descrever uma órbita circular fechada. Estas órbitas fechadas fazem parte de um conjunto de órbitas especiais chamadas órbitas esféricas de fótons [2121. S.V.C.B. Xavier, L.C.S. Leite, C.L. Benone, C.A.R. Herdeiro e L.C.B. Crispino, Rev. Bras. Ens. Fís. 42, e20200181 (2020).]. Neste contexto, é importante frisar que a sombra de um buraco negro não está associada ao seu horizonte de eventos, mas sim às órbitas esféricas de fótons que existem no exterior do buraco negro.
No caso da solução de Kerr, ou espaço-tempo de Kerr, podemos determinar analiticamente as equações que descrevem as órbitas esféricas de fótons e, consequentemente, a forma da sombra deste buraco negro. Isto só é possível devido a uma simetria existente no espaço-tempo de Kerr, representada matematicamente por um tensor de Killing2 2 Vetores e tensores de Killing indicam as direções nas quais o espaço-tempo possui simetria. Por exemplo, um espaço-tempo que possui simetria de translação temporal, admite um vetor de Killing na direção da coordenada temporal, o que acontece, por exemplo, na geometria de Minkowski. A existência de um vetor de Killing está também associada à conservação de uma grandeza ao longo de um movimento geodésico. não trivial de segunda ordem [11. R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984)., 22. S. Carroll, Spacetime and Geometry (Addison Wesley, San Francisco, 2004).].
Em espaços-tempos mais gerais, o cálculo analítico da sombra de um objeto compacto, como um buraco negro, pode não ser possível. Contudo, sempre é possível aplicar métodos numéricos para resolver as equações da geodésica e assim simular a sombra de um buraco negro vista por um observador. A técnica mais eficiente de simular a sombra de um buraco negro é o chamado de tracejamento inverso de raios3 3 Tradução do termo em inglês “Backwards ray-tracing”. . Esta técnica consiste em propagar os raios de luz para o passado, utilizando as equações da geodésica, a partir da localização do observador, até chegar à fonte emissora. Note que poderíamos propagar os raios de luz da fonte luminosa até a localização do observador no sentido real do tempo, no entanto este método se torna computacionalmente ineficiente, visto que a maioria dos raios de luz emitidos pela fonte não chega ao observador. Este mesmo método (associado ao tracejamento inverso de raios) também é utilizado com outras finalidades, por exemplo, para simular os gráficos em jogos de videogame na perspectiva de primeira pessoa.
Neste artigo buscamos apresentar, ao leitor com alguma familiaridade com a TRG, alguns detalhes da Física relacionada com a sombra de um buraco negro. Este artigo é, portanto, dirigido aos interessados em uma compreensão mais aprofundada sobre este tema de pesquisa atual e estimulante. Iniciamos com uma revisão das equações de movimento de raios de luz na geometria de Kerr. Abordamos as condições para a existência de um órbita esférica e suas propriedades. Também discutimos a forma da sombra de um buraco negro de Kerr com diferentes valores de momento angular, e utilizamos o método de tracejamento inverso de raios para simular computacionalmente a imagem de um buraco negro girante com e sem disco de acreção.
O restante deste artigo está organizado da seguinte forma: Na seção 2 2. O Espaço-Tempo de Kerr A solução exata que representa a geometria de um buraco negro girante foi encontrada na década de 1960 pelo matemático neozelandês Roy P. Kerr [9]. Devido ao momento angular não nulo do buraco negro, a solução de Kerr não possui simétria esférica, como é o caso da geometria de Schwarzschild. No entanto, a geometria de Kerr possui simetria axial em torno do eixo de rotação do buraco negro. O elemento de linha que descreve a separação infinitesimal de dois eventos no espaço-tempo de Kerr pode ser escrito, nas coordenadas de Boyer-Lindquist (t, r, θ, ϕ), como [3, 4]4 (1) d s 2 = g μ ν d x μ d x ν = - ( 1 - 2 M r Σ ) d t 2 + Σ Δ d r 2 - 2 2 M r a sin 2 θ Σ d t d ϕ + Σ d θ 2 + 𝒜 Σ sin 2 θ d ϕ 2 , onde μ,ν = t,r,θ,ϕ, e gμν são as componentes covariantes do tensor métrico. M é a massa do buraco negro e a é o momento angular por unidade de massa do buraco negro. As quantidades Σ,Δ e 𝒜 são funções das coordenadas (r,θ), dadas por (2) Σ ≡ r 2 + a 2 cos 2 θ , (3) Δ ≡ r 2 + a 2 - 2 M r , (4) 𝒜 ≡ ( r 2 + a 2 ) 2 - Δ a 2 sin 2 θ . O elemento de linha (1) é singular se Δ = 0 ou Σ = 0. No entanto, somente Σ = 0 corresponde a uma singularidade física do espaço-tempo. Em contraste, Δ = 0 é simplesmente uma singularidade aparente, consequência da escolha de coordenadas, e refere-se à localização dos horizontes nesta geometria, determinada por (5) r 2 + a 2 - 2 M r = 0 , cujas soluções são (6) r + ≡ M + ( M 2 - a 2 ) 1 2 , (7) r - ≡ M - ( M 2 - a 2 ) 1 2 . Denotamos o horizonte de eventos por r+, enquanto que r− corresponde a um horizonte de Cauchy [1]. Note que para r+ assumir somente valores reais, devemos ter (8) a 2 ≤ M 2 , o que restringe o parâmetro de rotação do buraco negro. A singularidade física da geometria de Kerr, Σ = 0, é determinada por (9) r 2 + a 2 cos 2 θ = 0 , que descreve um anel com raio a no plano equatorial (θ = π/2) [3]. É importante mencionar que quando tomamos o limite a→0 na Eq. (1), recuperamos a solução de Schwarzschild, que descreve um buraco negro descarregado e com simetria esférica [4]. Outra propriedade interessante sobre a métrica de Kerr é a existência da chamada ergoregião, que é formada pelas hipersuperfícies com a coordenada radial r situada no intervalo [1]: (10) r + < r < M + M 2 - a 2 cos 2 θ . Dentro da ergoregião, nenhum observador pode permanecer estático (mesmo sendo essa região localizada fora do horizonte de eventos) e tem necessariamente que estar em órbita no mesmo sentido de rotação do buraco negro. Este efeito é interpretado como uma manifestação extrema do arrasto dos referenciais inerciais [3]. Devido a Brandon Carter, sabe-se que é possível, no espaço-tempo de Kerr, escrever todas as equações das geodésicas como um sistema de equações diferenciais ordinárias de primeira ordem [22]. Este resultado é obtido utilizando-se o formalismo de Hamilton-Jacobi da mecânica clássica [24] no contexto da TRG e, em particular, no espaço-tempo de Kerr. Estas equações de movimento são dadas por5: (11) Σ 2 r . 2 = [ E ( r 2 + a 2 ) - a Φ ] 2 - Δ [ Q + ( a E - Φ ) 2 + m 2 r 2 ] , (12) Σ 2 θ . 2 = Q - cos 2 θ ( a 2 ( m 2 - E 2 ) + Φ 2 sin 2 θ ) , (13) Σ t . = E Δ [ ( r 2 + a 2 ) 2 - a 2 Δ sin 2 θ ] - 2 M a r Δ Φ , (14) Σ ϕ . = 2 M a E r Δ + Φ ( Δ - a 2 sin 2 θ ) Δ sin 2 θ , sendo m, E, Φ interpretados respectivamente como a massa de repouso, energia e momento angular em torno do eixo z de uma partícula, relativamente a um observador estático no infinito. Além destas quantidades, existe também a chamada constante de Carter Q, que pode ser relacionada com propriedades do movimento na coordenada θ [23]. Utilizamos a notação na qual pontos sobre variáveis denotam derivadas em relação ao parâmetro afim ao longo da geodésica. , revisamos a geometria de Kerr e algumas de suas propriedades. A seção 3 3. Órbitas Esféricas de Fótons Nesta seção analisamos as órbitas esféricas de fótons no espaço-tempo de Kerr [21]. Estas órbitas possuem como principal característica o fato de a coordenada radial de Boyer-Lindquist ser constante. Levando em consideração que fótons possuem massa de repouso nula (m = 0), as equações de movimento (11) e (12), se reduzem a (15) R ≡ Σ 2 r . 2 = [ E ( r 2 + a 2 ) - a Φ ] 2 - Δ [ Q + ( a E - Φ ) 2 ] , (16) Σ 2 θ . 2 = Θ ( θ ) = Q - cos 2 θ ( Φ 2 sin 2 θ - a 2 E 2 ) , enquanto que as equações de movimento (13) e (14), se mantêm inalteradas. Podemos reduzir o número de parâmetros constantes nas Eqs. (15) e (16) dividindo-as pelo fator E2. Definindo os parâmetros (17) ξ ≡ Φ E , (18) η ≡ Q E 2 , encontramos que (19) ℛ ≡ R E 2 = [ ( r 2 + a 2 ) - a ξ ] 2 - Δ [ η + ( a - ξ ) 2 ] , (20) Θ E 2 = η - cos 2 θ ( ξ 2 sin 2 θ - a 2 ) . Expandindo os termos quadrados da Eq. (19) e coletando as potências de r, temos (21) ℛ = r 4 + ( a 2 - η - ξ 2 ) r 2 + 2 M ( η + ( a - ξ ) 2 ) r - a 2 η . A condição para órbitas esféricas de fótons é dada por (22) r . = 0 , (23) r ¨ = 0 , isto é, a “velocidade” (r.) e “aceleração” (r¨) na coordenada radial são nulas, em analogia com a mecânica clássica. Levando-se em consideração as Eqs. (15) e (19), temos (24) ℛ = Σ 2 r . 2 E 2 . Assim, a condição (22) implica que (25) r . = 0 ⇔ ℛ = 0 . Além disso, derivando a Eq. (24) com relação ao parâmetro afim ao longo da geodésica, temos (26) d ℛ d r = 2 Σ 2 r ¨ E 2 + d d r ( Σ 2 ) r . 2 E 2 , onde utilizamos a regra da cadeia ddλ=r.ddr. Considerando a condição (22) na Eq. (26), obtemos que (27) d ℛ d r = 2 Σ 2 r ¨ E 2 . Desta forma, a condição (23) implica que (28) r ¨ = 0 ⇔ d ℛ d r = 0 . Concluímos que as órbitas esféricas de fótons satisfazem as seguintes condições: (29) ℛ = 0 , (30) d ℛ d r = 0 . Substituindo a Eq. (21) nas Eqs. (29) e (30), obtemos (31) r 4 + ( a 2 - η - ξ 2 ) r 2 + 2 M ( η + ( a - ξ ) 2 ) r - a 2 η = 0 , (32) 4 r 3 + 2 ( a 2 - η - ξ 2 ) r + 2 M ( η + ( a - ξ ) 2 ) = 0 . O conjunto das Eqs. (31) e (32) pode ser reescrito como (33) 3 r 4 + a 2 r 2 - η ( r 2 - a 2 ) = r 2 ξ 2 , (34) r 4 - a 2 M r + η ( a 2 - M r ) = M r ( ξ 2 - 2 a ξ ) , sendo que a Eq. (33) foi obtida multiplicando a Eq. (32) por r e subtraindo o resultado pela Eq. (31). Já a Eq. (34) foi obtida multiplicando a Eq. (32) por r e subtraindo o resultado pela Eq. (31) multiplicada por 2. A solução para {η,ξ}, que satisfaz o conjunto de Eqs. (33) e (34), é (35) η c ≡ r 3 ( 4 M Δ - r ( r - M ) 2 ) a 2 ( r - M ) 2 , (36) ξ c ≡ M ( r 2 - a 2 ) - r Δ a ( r - M ) , onde r ∈ [r1,r2], e (37) r 1 ≡ 2 M [ 1 + cos ( 2 3 arccos [ - ∣ a ∣ M ] ) ] , (38) r 2 ≡ 2 M [ 1 + cos ( 2 3 arccos [ ∣ a ∣ M ] ) ] , são as raízes de ηc, visto que as órbitas esféricas de fótons só correspondem a soluções físicas para ηc≥0 [25]. Estas raízes obedecem a seguinte equação cúbica: (39) r 3 - 6 M r 2 + 9 M 2 r - 4 a 2 M = 0 , que possui 3 raízes reais. Contudo, é possível mostrar que uma destas raízes (r_3) está localizada dentro do horizonte de eventos. Sendo assim, r_3 não tem implicação no movimento de fótons que estão localizados fora do horizonte de eventos e pode ser descartada. Ressaltamos que η e ξ são constantes do movimento para cada órbita esférica. As Eqs. (35) e (36) expressam qual o valor destas constantes para haver uma órbita esférica de fótons em uma determinada coordenada radial r ∈ [r1,r2]. Além disso, estas órbitas esféricas de fótons são instáveis, pois d2ℛ/dr2 > 0 [23]. Para a=0, temos r1 = r2 = 3M, que é a localização da órbita circular instável para fótons no espaço-tempo de Schwarzschild [1]. Na Fig. 3 exibimos o gráfico dos parâmetros ηc e ξc em função de r/M, com a = 0.8M. Figura 3 Parâmetros {ηc,ξc} em termos do raio r ∈ [r1,r2] das órbitas esféricas de fótons ao redor do buraco negro de Kerr. Nesta figura adotamos a = 0.8M. A constante ηc está relacionada ao movimento na direção da coordenada θ, enquanto que ξc é o momento angular do fóton em torno do eixo z, por unidade de energia. Quando ηc = 0, as órbitas esféricas de fótons têm seu movimento restrito ao plano equatorial. Além disso, estas órbitas, restritas ao plano equatorial, são descritas no mesmo sentido de rotação do buraco negro, no caso em que ξc > 0, e no sentido oposto, no caso em que ξc < 0, constituindo as chamadas órbitas co-girantes e contra-girantes, respectivamente. Órbitas planares de fótons estão presentes em outras geometrias, além da associada à solução de Kerr. A existência destas órbitas é uma característica geral de buracos negros que são estacionários, possuem simetria axial e cuja geometria tende a do espaço-tempo de Minkowski longe da origem da coordenada radial [26]. Ilustrações de diversas órbitas esféricas de fótons na geometria de Kerr podem ser encontradas na Ref. [21]. é dedicada às órbitas esféricas de fótons, enquanto que na seção 4 4. Sombras de Buracos Negros Observadores locais na geometria de Kerr Iniciamos esta seção tratando de um referencial ligado a um observador local na geometria de Kerr. Podemos descrever como este observador mede as componentes do quadri-momento de um determinado fóton, além de sua percepção visual da sombra de um buraco negro de Kerr. Restringimos a nossa análise à classe de observadores denominada OMAN, que é uma abreviatura para o termo “Observador com Momento Angular Nulo”6. Um OMAN é descrito pela seguinte base tétrada [27] (40) e ^ ( t ) = ζ ∂ t + γ ∂ ϕ , (41) e ^ ( r ) = 1 g r r ∂ r , (42) e ^ ( θ ) = 1 g θ θ ∂ θ , (43) e ^ ( ϕ ) = 1 g ϕ ϕ ∂ ϕ , onde (44) ζ ≡ g ϕ ϕ g t ϕ 2 - g t t g ϕ ϕ , (45) γ ≡ - g t ϕ g ϕ ϕ g ϕ ϕ g t ϕ 2 - g t t g ϕ ϕ . O vetor e^(t) está relacionado à quadri-velocidade deste observador, enquanto que os vetores (e^(r),e^(θ),e^(ϕ)), dados nas Eqs. (41)–(43), são as direções espaciais do sistema de referência do observador, conforme mostrado na Fig. 4. A medida da energia de um fóton no referencial de um OMAN é obtida projetando-se o quadri-momento deste fóton na direção e^(t), isto é: Figura 4 Representação da decomposição do momento linear de um fóton na base (e^(r), e^(θ), e^(φ)). Esta decomposição é feita em função dos ângulos (α, β), onde α é o ângulo formado entre o tri-momento linear P→ e o plano gerado pelos versores e^(r) e e^(φ) (plano e^(r)⟂e^(φ)), enquanto que β é o ângulo que a projeção vertical de P→ no plano e^(r)⟂e^(φ) faz com o versor e^(r). O buraco negro está representado pela esfera à direita. Imagem publicada originalmente na Ref. [29]. (46) p ( t ) = - e ^ ( t ) μ p μ = - ( ζ p t + γ p ϕ ) = ζ E - γ Φ . Também podemos calcular a projeção do quadri-momento de um fóton nas direções espaciais e^r, e^θ e e^ϕ. Estas quantidades são interpretadas como as componentes do momento linear do fóton, conforme medido pelo OMAN, que são dadas por: (47) p ( r ) = e ^ r μ p μ = p r g r r , (48) p ( θ ) = e ^ θ μ p μ = p θ g θ θ , (49) p ( ϕ ) = e ^ ϕ μ p μ = Φ g ϕ ϕ . Da Eq. (49), notamos que um fóton com momento angular nulo em relação a um observador estático no infinito (Φ = 0) também terá momento angular nulo em relação ao OMAN. Isto acontece porque a classe OMAN possui momento angular nulo em relação a um observador estático no infinito, como o próprio nome sugere. A Sombra de um Buraco Negro de Kerr O OMAN pode projetar os fótons recebidos em um determinado plano cartesiano. Podemos atribuir a cada fóton detectado no sistema de referência deste observador um par de coordenadas cartesianas (x, y). Estas coordenadas cartesianas definem o parâmetro de impacto de um fóton [28], que por sua vez é uma função dos ângulos α e β, descritos na Fig. 4. O ângulo sólido de um objeto, por exemplo um buraco negro, medido no referencial do observador, depende da distância entre os dois. Para medir a distância entre o objeto e o observador, utilizamos a definição do raio perimetral, que é um invariante geométrico, dado por [27, 29]: (50) r ~ ≡ 1 2 π ∫ 0 2 π g ϕ ϕ d ϕ | θ = π / 2 = g ϕ ϕ | θ = π / 2 , onde usamos que o integrando da Eq. (50) não depende da coordenada ϕ, o que está associado à simetria axial do espaço-tempo. O raio perimetral, que é calculado na coordenada radial do observador situado em r_0, é uma medida possível para a distância entre o centro do buraco negro e o observador. Os ângulos de observação (α, β) do buraco negro no referencial OMAN têm uma dependência no raio perimetral na forma de 1/r~ para observadores muito distantes do buraco negro. Isto implica que estes ângulos α e β são muito pequenos nesse limite.7 Neste regime, o par (x, y) pode ser escrito como8 (51) x ≈ - r ~ β , (52) y ≈ r ~ α . Denotando por P→ o tri-momento linear do fóton, i. e. (53) P → ≡ ( p ( r ) , p ( θ ) , p ( ϕ ) ) , cuja norma é (54) P 2 = ( p ( r ) ) 2 + ( p ( θ ) ) 2 + ( p ( ϕ ) ) 2 , podemos calcular suas componentes em função dos ângulos α e β, dadas por (ver Fig. 4): (55) p ( ϕ ) = P cos α sin β , (56) p ( θ ) = P sin α , (57) p ( r ) = P cos α cos β . Além disso, como fótons têm massa de repouso nula, i. e., Pμ = 0, logo P = p(t). Esta constante P não influencia na trajetória descrita por um fóton, e pode ser associada com a frequência deste, medida pelo observador. Podemos escrever os ângulos α e β, presentes nas Eqs. (51) e (52), em termos das componentes do momento linear do fóton. Na aproximação de um observador muito distante do buraco negro, obtemos, das Eqs. (55) e (56), que: (58) β ≈ p ( ϕ ) P = p ( ϕ ) p ( t ) , (59) α ≈ p ( θ ) P = p ( θ ) p ( t ) . Utilizando as Eqs. (46)–(49) nas Eqs. (58) e (59), e substituindo o resultado nas Eqs. (51)–(52), obtemos (60) x = - ξ sin θ 0 , (61) y = η + a 2 cos 2 θ 0 - ξ 2 tan 2 θ 0 , onde θ0 determina a localização do observador na coordenada θ. Para determinar a sombra de um buraco negro de Kerr, η e ξ presentes nas Eqs. (60)–(61) são interpretados matematicamente como funções paramétricas de r, determinadas pelas Eqs. (35)–(36). Para r ∈ [r1,r2], a sombra de um buraco negro de Kerr está apresentada na Fig. 5, para diferentes escolhas do parâmetro de rotação, vista por um observador no infinito e no plano equatorial. Figura 5 Sombra de um buraco negro de Kerr descrita por um observador localizado muito distante do buraco negro (r~≫M) e no plano equatorial θ0 = π/2. Nesta figura escolhemos cinco valores para o parâmetro de rotação a do buraco negro. Da Fig. 5, vemos que quanto mais próximo do valor de rotação máximo permitido para um buraco negro [ver Eq. (8)], mais assimétrica é a sombra de um buraco negro de Kerr. Para a = 0.999M, a sombra do buraco negro se assemelha com a forma da letra “D”. Nas medidas obtidas pelo THE (cf. Fig. 1), o raio gravitacional do buraco negro supermassivo corresponde a uma escala angular de θg = 3.8 ± 0.4μas [10, 14, 15]. Como mencionamos anteriormente, este buraco negro, que está localizado no centro da galáxia Messier 87, possui uma massa estimada [10] de MBH = (6.5 ± 0.7)×109M⊙, onde M⊙ = 1,989×1030kg é a massa do Sol. discutimos a obtenção analítica da sombra de um buraco negro de Kerr. Na seção 5 5. Tracejamento Inverso de Raios Na seção 4, vimos que é possível encontrar analiticamente a forma da sombra de um buraco negro de Kerr. Isto acontece devido às simetrias presentes neste espaço-tempo, codificadas na existência dos vetores de Killing nas direções t e ϕ, e na existência de um tensor de Killing não trivial Kμ ν, que dá origem à constante de Carter Q9. No entanto, um espaço-tempo genérico não possui uma constante de Carter, e como consequência não é possível encontrar a sombra de um buraco negro de maneira analítica. Um exemplo deste fato são os buracos negros de Kerr com cabelo escalar [31]. Nestas situações, podemos analisar as equações da geodésica, dadas por [3] (62) d 2 x α d τ 2 + Γ μ ν α d x μ d τ d x ν d τ = 0 . Estas equações, que são válidas independentemente das simetrias do espaço-tempo, consistem em um sistema de equações diferenciais ordinárias com derivadas de segunda ordem em relação ao parâmetro afim τ. Assumindo um espaço-tempo estacionário e com simetria axial, podemos escrever que (63) r ¨ + Γ t t r t . 2 + Γ r r r r . 2 + Γ θ θ r θ . 2 + Γ ϕ ϕ r ϕ . 2 + 2 Γ t ϕ r t . ϕ . + 2 Γ r θ r r . θ . = 0 , (64) θ ¨ + Γ t t θ t . 2 + Γ r r θ r . 2 + Γ θ θ θ θ . 2 + Γ ϕ ϕ θ ϕ . 2 + 2 Γ t ϕ θ t . ϕ . + 2 Γ r θ θ r . θ . = 0 , (65) t . = - E g t t + Φ g t ϕ , (66) ϕ . = - E g t ϕ + Φ g ϕ ϕ . Com o intuito de determinar a sombra de um buraco negro estacionário e com simetria axial, usamos o método de tracejamento inverso de raios. Este método eficiente consiste em evoluir os raios de luz, a partir das coordenadas do observador, para trás no tempo e detetar a origem de cada raio de luz. Para integrar numericamente as Eqs. (63)–(66), precisamos impor condições iniciais. Visto que evoluímos os raios de luz para trás no tempo, as condições iniciais são dadas pelo quadri-vetor posição do fóton10 (t0, r0, θ0, ϕ0) e pelo quadri-momento do fóton na posição do observador, a saber: (67) Φ = g ϕ ϕ sin β cos α , (68) E = ( 1 + γ g ϕ ϕ sin β cos α ζ ) , (69) p r = g r r cos β cos α , (70) p θ = g θ θ sin α , onde utilizamos as Eqs. (46)–(49) e (55)–(57). Além das condições iniciais, devemos decidir quando terminar a integração numérica de um determinado raio de luz. Quando um raio de luz chega muito próximo do horizonte de eventos do buraco negro (r≈r+), interrompemos a integração numérica e consideramos este raio como sendo absorvido pelo buraco negro. Caso o raio de luz tenha coordenada radial muito maior que a do horizonte de eventos, por exemplo r≈30M, consideramos que este raio escapou da atração gravitacional do buraco negro, ou seja, é um caso de espalhamento, e interrompemos a integração numérica. Com o intuito de distinguir os raios espalhados dos raios absorvidos, supomos que há uma esfera celeste de raio r = 30M emitindo luz de maneira isotrópica. Podemos escolher um padrão para a esfera celeste, que destaque os efeitos de lentes gravitacionais. Este padrão depende somente das coordenadas (θ,ϕ). Na Fig. 6, adotamos um padrão do tipo “xadrez”, e mostramos a percepção visual de um observador no espaço-tempo de Minkowski (sem a presença de um buraco negro). Figura 6 Percepção visual da esfera celeste, representada com um padrão tipo “xadrez”. Nesta imagem o observador está no espaço-tempo de Minkowski (sem a presença de um buraco negro). Na presença de um buraco negro, descrito, por exemplo, pela métrica de Kerr, a percepção visual de um observador é, em geral, diferente de um espaço-tempo plano. Esta variação se deve não somente à presença da sombra do buraco negro, mas também devido aos efeitos de lente gravitacional. Na Fig. 7, exemplificamos a percepção visual de um observador na presença de um buraco negro de Kerr, utilizando o mesmo padrão da Fig. 6. Utilizamos o método de tracejamento inverso de raios para a métrica de Kerr com a=M, isto é, um buraco negro de Kerr extremo. Além disso, ressaltamos que nas Figs. 6 e 7 o observador está localizado no plano equatorial (θ0 = π/2) e possui raio perimetral r~=15M. Figura 7 Percepção visual de um observador nas mesmas condições que as da Fig. 6, porém na presença de um buraco negro. Para esta imagem utilizamos o método de tracejamento inverso de raios para um buraco negro de Kerr extremo (a = M). Apesar de podermos estudar a sombra e o efeito de lente gravitacional do buraco negro de Kerr adotando o padrão “xadrez” para a esfera celeste, esta é uma configuração puramente acadêmica. Configurações astronômicas mais realistas levam em conta a presença de matéria ao redor do buraco negro, em particular discos de acreção. Estes discos são formados por matéria difusa orbitando o buraco negro. As primeiras simulações computacionais do aspecto visual de buracos negros com matéria ao redor foram feitas assumindo um disco de acreção fino orbitando um buraco negro de Schwarzschild [32]. Podemos considerar outros modelos para descrever o disco de acreção. Neste trabalho, consideramos o modelo de Page-Thorne, que é um modelo idealizado de disco de acreção, onde as partículas que constituem o disco estão restritas a um movimento circular ao longo do plano equatorial [33]. Nas Figs. 8 e 9, apresentamos a sombra de buracos negros de Kerr com um disco de acreção de Page-Thorne. Para gerarmos as simulações exibidas nas Figs. 8 e 9, utilizamos o software GYOTO (General relativitY Orbit Tracer of Observatoire de Paris) [34]. Este software contém suporte para tracejamento inverso de raios em vários espaços-tempos, dentre eles o espaço-tempo de Kerr. Além disso, o software GYOTO permite a simulação de vários objetos astrofísicos, por exemplo, buracos negros com disco de acreção de Page-Thorne11. Figura 8 Tracejamento inverso de raios no espaço-tempo de Kerr com um disco de acreção de Page-Thorne ao seu redor. O parâmetro de rotação do buraco negro foi fixado em a = 0.5M. O observador está localizado em θ0 = 85°, isto é, ligeiramente acima do plano equatorial. Figura 9 Tracejamento inverso de raios no espaço-tempo de Kerr com um disco de acreção de Page-Thorne ao seu redor. Na imagem da esquerda representamos um buraco negro com parâmetro de rotação a = 0.94M, com o observador localizado em θ0 = 17°. Na imagem da direita aplicamos um filtro de desfocagem Gaussiano à imagem da esquerda, como uma tentativa simplificada de reproduzir as condições de observação do THE. De forma a obter uma melhor comparação com a imagem do THE exibida na Fig. 1, a orientação destas imagens foi modificada relativamente à da Fig. 8. Na Fig. 8, escolhemos o parâmetro de rotação do buraco negro de Kerr como sendo a = 0.5M. O observador foi posicionado em θ0 = 85°, ou seja, ligeiramente fora do plano equatorial. Este observador consegue visualizar a parte que está “atrás” do buraco negro, devido aos efeitos de lente gravitacional que geram uma posição aparente de parte do disco de acreção acima do buraco negro. Curiosamente, há uma maior intensidade dos raios de luz no lado esquerdo da imagem, em comparação ao lado direito. Isto acontece devido à rotação do buraco negro e ao efeito Doppler e Liouville [5]. O efeito Doppler consiste na mudança da frequência observada de uma onda quando há movimento relativo entre fonte e observador. Em particular, a análise do efeito Doppler em ondas eletromagnéticas nos permite inferir a velocidade de afastamento ou aproximação de estrelas e galáxias. Estas medidas tornaram possível, por exemplo, a descoberta da expansão do universo. Já o efeito Liouville é a mudança na intensidade de uma onda devido ao movimento relativo entre fonte e observador. Este fenômeno é consequência do teorema de Liouville sobre a conservação do volume no espaço de fase [24]. De forma a fazer uma melhor comparação com a imagem de M87* obtida pelo THE, na Fig. 9 está representada a imagem de um buraco negro de Kerr com a = 0.94M, circundado por um disco de acreção de Page-Thorne, visto com um ângulo de θo = 17° (parâmetros correspondentes aos da imagem da Fig. 1). Uma vez que o THE tem uma resolução de observação limitada, também aplicamos um filtro Gaussiano de desfocagem sobre a imagem obtida pelo GYOTO. Este procedimento muito simplificado procura reproduzir a imagem obtida pelo THE. Podemos comparar o resultado desta simulação com a imagem observada pelo THE na Fig. 1, sendo notável a semelhança. Nas simulações publicadas pela colaboração internacional THE, considerou-se como modelo para o disco de acreção um gás a alta temperatura e magnetizado ao redor do buraco negro. A obtenção da imagem da sombra de um buraco negro pelo THE, juntamente com as deteções de ondas gravitacionais [36], marcam o início das confirmações experimentais da gravitação em regime de campo forte, que estão consistentes com os resultados previstos pela TRG. , discutimos o método de tracejamento inverso de raios e apresentamos as simulações da aparência de um buraco negro girante. Finalizamos este artigo com nossas conclusões apresentadas na seção 6 6. Conclusões Neste trabalho analisamos as sombras de buracos negros de Kerr. Estas sombras são obtidas a partir do conjunto das órbitas esféricas de fótons presentes neste espaço-tempo. Com as equações de movimento no espaço-tempo de Kerr, analisamos o movimento de fótons, que possuem massa de repouso nula. A partir disso, mostramos que existem órbitas cuja coordenada radial permanece constante, que são denominadas órbitas esféricas de fótons. O conjunto das órbitas esféricas de fótons determina a sombra do buraco negro. Apresentamos a forma analítica da sombra de um buraco negro de Kerr, bem como seu aspecto visual, assim como visto por um observador distante. A forma da sombra do buraco negro de Kerr para valores de rotação muito baixo é aproximadamente circular. Conforme o parâmetro de rotação do buraco negro aumenta, a sombra se torna assimétrica. Para um buraco negro de Kerr extremo, temos uma sombra que se assemelha ao formato da letra “D”. Também discutimos o método de tracejamento inverso de raios, que consiste em resolver numericamente as equações da geodésica com a finalidade de obter uma imagem da sombra de um buraco negro. Este método é particularmente importante quando não é possível determinar a forma analítica da sombra de um buraco negro. Primeiramente, consideramos apenas o buraco negro com a esfera celeste ao seu redor. Nesta esfera celeste adotou-se um padrão regular tipo “xadrez”, que depende das coordenadas (θ,ϕ). Desta forma, obtivemos a percepção visual de um observador ao redor deste buraco negro, isto é, o formato da sombra e os efeitos de lente gravitacional. Como uma ilustração adicional, na Fig. 10 o padrão da esfera celeste foi substituído pelo símbolo da Revista Brasileira de Ensino de Física. Figura 10 Tracejamento inverso de raios utilizando o símbolo da Revista Brasileira de Ensino de Física como padrão para a esfera celeste. Nesta figura, temos um buraco negro de Kerr extremo (a=M), o observador está localizado no plano equatorial com coordenada radial r0 = 10M e a esfera celeste tem raio 20M. Para descrever situações astronômicas mais realistas, ilustramos o método de tracejamento inverso de raios para um buraco negro de Kerr com um disco de acreção. Este disco de acreção foi descrito pelo modelo de Page-Thorne. Nesta configuração mais próxima dos casos astrofísicos, vários fenômenos interessantes podem ser constatados. Por exemplo, a possibilidade de o observador ver “a parte de trás” do disco de acreção, devido aos efeitos de lente gravitacional, e a diferença de intensidade dos raios de luz provenientes do disco de acreção, causada por efeitos Doppler e Liouville. . No decorrer deste artigo, utilizamos a assinatura (−, +, +, +) para a métrica, e adotamos as unidades nas quais a velocidade da luz e a constante da gravitação universal de Newton são iguais à unidade. Adotamos também a convenção de soma de Einstein, na qual a presença de índices repetidos implica na existência de um somatório sobre estes índices.
2. O Espaço-Tempo de Kerr
A solução exata que representa a geometria de um buraco negro girante foi encontrada na década de 1960 pelo matemático neozelandês Roy P. Kerr [99. R.P. Kerr, Phys. Rev. Lett. 11, 237 (1963).]. Devido ao momento angular não nulo do buraco negro, a solução de Kerr não possui simétria esférica, como é o caso da geometria de Schwarzschild. No entanto, a geometria de Kerr possui simetria axial em torno do eixo de rotação do buraco negro. O elemento de linha que descreve a separação infinitesimal de dois eventos no espaço-tempo de Kerr pode ser escrito, nas coordenadas de Boyer-Lindquist (t, r, θ, ϕ), como [33. M.P. Hobson, G.P. Efstathiou e A.N. Lasenby, General Relativity: an Introduction for Physicists (Cambridge University Press, Cambridge, 2006)., 44. R. D’Inverno, Introducing Einstein’s Relativity (Clarendon Press, Oxford, 1992).]4 4 As coordenadas de Boyer-Lindquist são coordenadas do tipo esferoidais oblatas e são úteis para tratar diversos aspectos do espaço-tempo de Kerr como, por exemplo, o estudo de geodésicas nulas. Nestas coordenadas, o único termo não-diagonal é gt ϕ, que é responsável por efeitos interessantes na métrica de Kerr, como é o caso do arrasto dos referenciais inerciais, que ocorre quando um referencial inercial é arrastado no mesmo sentido de rotação do buraco negro.
onde μ,ν = t,r,θ,ϕ, e gμν são as componentes covariantes do tensor métrico. M é a massa do buraco negro e a é o momento angular por unidade de massa do buraco negro. As quantidades Σ,Δ e 𝒜 são funções das coordenadas (r,θ), dadas por
O elemento de linha (1) é singular se Δ = 0 ou Σ = 0. No entanto, somente Σ = 0 corresponde a uma singularidade física do espaço-tempo. Em contraste, Δ = 0 é simplesmente uma singularidade aparente, consequência da escolha de coordenadas, e refere-se à localização dos horizontes nesta geometria, determinada por
cujas soluções são
Denotamos o horizonte de eventos por r+, enquanto que r− corresponde a um horizonte de Cauchy [11. R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984).]. Note que para r+ assumir somente valores reais, devemos ter
o que restringe o parâmetro de rotação do buraco negro.
A singularidade física da geometria de Kerr, Σ = 0, é determinada por
que descreve um anel com raio a no plano equatorial (θ = π/2) [33. M.P. Hobson, G.P. Efstathiou e A.N. Lasenby, General Relativity: an Introduction for Physicists (Cambridge University Press, Cambridge, 2006).]. É importante mencionar que quando tomamos o limite a→0 na Eq. (1), recuperamos a solução de Schwarzschild, que descreve um buraco negro descarregado e com simetria esférica [44. R. D’Inverno, Introducing Einstein’s Relativity (Clarendon Press, Oxford, 1992).].
Outra propriedade interessante sobre a métrica de Kerr é a existência da chamada ergoregião, que é formada pelas hipersuperfícies com a coordenada radial r situada no intervalo [11. R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984).]:
Dentro da ergoregião, nenhum observador pode permanecer estático (mesmo sendo essa região localizada fora do horizonte de eventos) e tem necessariamente que estar em órbita no mesmo sentido de rotação do buraco negro. Este efeito é interpretado como uma manifestação extrema do arrasto dos referenciais inerciais [33. M.P. Hobson, G.P. Efstathiou e A.N. Lasenby, General Relativity: an Introduction for Physicists (Cambridge University Press, Cambridge, 2006).].
Devido a Brandon Carter, sabe-se que é possível, no espaço-tempo de Kerr, escrever todas as equações das geodésicas como um sistema de equações diferenciais ordinárias de primeira ordem [2222. B. Carter, Phys. Rev. 174, 1559 (1968).]. Este resultado é obtido utilizando-se o formalismo de Hamilton-Jacobi da mecânica clássica [2424. N.A. Lemos, Mecânica analítica (Editora Livraria da Física, São Paulo, 2007).] no contexto da TRG e, em particular, no espaço-tempo de Kerr. Estas equações de movimento são dadas por5 5 Para uma dedução das Eqs. (11)–(14), utilizando o formalismo de Hamilton-Jacobi no contexto da TRG recomendamos a Ref. [21]. :
sendo m, E, Φ interpretados respectivamente como a massa de repouso, energia e momento angular em torno do eixo z de uma partícula, relativamente a um observador estático no infinito. Além destas quantidades, existe também a chamada constante de Carter Q, que pode ser relacionada com propriedades do movimento na coordenada θ [2323. D.C. Wilkins, Phys. Rev. D. 5, 814 (1972).]. Utilizamos a notação na qual pontos sobre variáveis denotam derivadas em relação ao parâmetro afim ao longo da geodésica.
3. Órbitas Esféricas de Fótons
Nesta seção analisamos as órbitas esféricas de fótons no espaço-tempo de Kerr [2121. S.V.C.B. Xavier, L.C.S. Leite, C.L. Benone, C.A.R. Herdeiro e L.C.B. Crispino, Rev. Bras. Ens. Fís. 42, e20200181 (2020).]. Estas órbitas possuem como principal característica o fato de a coordenada radial de Boyer-Lindquist ser constante. Levando em consideração que fótons possuem massa de repouso nula (m = 0), as equações de movimento (11) e (12), se reduzem a
enquanto que as equações de movimento (13) e (14), se mantêm inalteradas.
Podemos reduzir o número de parâmetros constantes nas Eqs. (15) e (16) dividindo-as pelo fator E2. Definindo os parâmetros
encontramos que
Expandindo os termos quadrados da Eq. (19) e coletando as potências de r, temos
A condição para órbitas esféricas de fótons é dada por
isto é, a “velocidade” () e “aceleração” () na coordenada radial são nulas, em analogia com a mecânica clássica. Levando-se em consideração as Eqs. (15) e (19), temos
Assim, a condição (22) implica que
Além disso, derivando a Eq. (24) com relação ao parâmetro afim ao longo da geodésica, temos
onde utilizamos a regra da cadeia . Considerando a condição (22) na Eq. (26), obtemos que
Desta forma, a condição (23) implica que
Concluímos que as órbitas esféricas de fótons satisfazem as seguintes condições:
Substituindo a Eq. (21) nas Eqs. (29) e (30), obtemos
O conjunto das Eqs. (31) e (32) pode ser reescrito como
sendo que a Eq. (33) foi obtida multiplicando a Eq. (32) por r e subtraindo o resultado pela Eq. (31). Já a Eq. (34) foi obtida multiplicando a Eq. (32) por r e subtraindo o resultado pela Eq. (31) multiplicada por 2.
A solução para {η,ξ}, que satisfaz o conjunto de Eqs. (33) e (34), é
onde r ∈ [r1,r2], e
são as raízes de ηc, visto que as órbitas esféricas de fótons só correspondem a soluções físicas para ηc≥0 [2525. E. Teo, Gen. Relativ. Gravit. 35, 1909 (2003).]. Estas raízes obedecem a seguinte equação cúbica:
que possui 3 raízes reais. Contudo, é possível mostrar que uma destas raízes (r_3) está localizada dentro do horizonte de eventos. Sendo assim, r_3 não tem implicação no movimento de fótons que estão localizados fora do horizonte de eventos e pode ser descartada. Ressaltamos que η e ξ são constantes do movimento para cada órbita esférica. As Eqs. (35) e (36) expressam qual o valor destas constantes para haver uma órbita esférica de fótons em uma determinada coordenada radial r ∈ [r1,r2]. Além disso, estas órbitas esféricas de fótons são instáveis, pois d2ℛ/dr2 > 0 [2323. D.C. Wilkins, Phys. Rev. D. 5, 814 (1972).]. Para a=0, temos r1 = r2 = 3M, que é a localização da órbita circular instável para fótons no espaço-tempo de Schwarzschild [11. R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984).]. Na Fig. 3 exibimos o gráfico dos parâmetros ηc e ξc em função de r/M, com a = 0.8M.
Parâmetros {ηc,ξc} em termos do raio r ∈ [r1,r2] das órbitas esféricas de fótons ao redor do buraco negro de Kerr. Nesta figura adotamos a = 0.8M.
A constante ηc está relacionada ao movimento na direção da coordenada θ, enquanto que ξc é o momento angular do fóton em torno do eixo z, por unidade de energia. Quando ηc = 0, as órbitas esféricas de fótons têm seu movimento restrito ao plano equatorial. Além disso, estas órbitas, restritas ao plano equatorial, são descritas no mesmo sentido de rotação do buraco negro, no caso em que ξc > 0, e no sentido oposto, no caso em que ξc < 0, constituindo as chamadas órbitas co-girantes e contra-girantes, respectivamente. Órbitas planares de fótons estão presentes em outras geometrias, além da associada à solução de Kerr. A existência destas órbitas é uma característica geral de buracos negros que são estacionários, possuem simetria axial e cuja geometria tende a do espaço-tempo de Minkowski longe da origem da coordenada radial [2626. P.V.P. Cunha e C.A.R. Herdeiro, Phys. Rev. Lett. 124, 181191 (2020).]. Ilustrações de diversas órbitas esféricas de fótons na geometria de Kerr podem ser encontradas na Ref. [2121. S.V.C.B. Xavier, L.C.S. Leite, C.L. Benone, C.A.R. Herdeiro e L.C.B. Crispino, Rev. Bras. Ens. Fís. 42, e20200181 (2020).].
4. Sombras de Buracos Negros
Observadores locais na geometria de Kerr
Iniciamos esta seção tratando de um referencial ligado a um observador local na geometria de Kerr. Podemos descrever como este observador mede as componentes do quadri-momento de um determinado fóton, além de sua percepção visual da sombra de um buraco negro de Kerr. Restringimos a nossa análise à classe de observadores denominada OMAN, que é uma abreviatura para o termo “Observador com Momento Angular Nulo”6 6 A abreviatura correspondente em inglês é ZAMO, correspondendo ao termo “Zero Angular Momentum Observer”. . Um OMAN é descrito pela seguinte base tétrada [2727. P.V.P. Cunha e C.A.R. Herdeiro, Gen. Relativ. Grav. 50, 42 (2018).]
onde
O vetor está relacionado à quadri-velocidade deste observador, enquanto que os vetores , dados nas Eqs. (41)–(43), são as direções espaciais do sistema de referência do observador, conforme mostrado na Fig. 4. A medida da energia de um fóton no referencial de um OMAN é obtida projetando-se o quadri-momento deste fóton na direção , isto é:
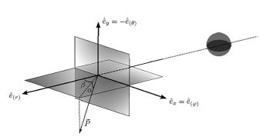
Representação da decomposição do momento linear de um fóton na base (, , . Esta decomposição é feita em função dos ângulos (α, β), onde α é o ângulo formado entre o tri-momento linear e o plano gerado pelos versores e (plano ), enquanto que β é o ângulo que a projeção vertical de no plano faz com o versor . O buraco negro está representado pela esfera à direita. Imagem publicada originalmente na Ref. [2929. P.V.P. Cunha, C.A.R. Herdeiro, E. Radu e H. Runarsson, Int. J. Mod. Phys. D 25, 1641021 (2016).].
Também podemos calcular a projeção do quadri-momento de um fóton nas direções espaciais , e . Estas quantidades são interpretadas como as componentes do momento linear do fóton, conforme medido pelo OMAN, que são dadas por:
Da Eq. (49), notamos que um fóton com momento angular nulo em relação a um observador estático no infinito (Φ = 0) também terá momento angular nulo em relação ao OMAN. Isto acontece porque a classe OMAN possui momento angular nulo em relação a um observador estático no infinito, como o próprio nome sugere.
A Sombra de um Buraco Negro de Kerr
O OMAN pode projetar os fótons recebidos em um determinado plano cartesiano. Podemos atribuir a cada fóton detectado no sistema de referência deste observador um par de coordenadas cartesianas (x, y). Estas coordenadas cartesianas definem o parâmetro de impacto de um fóton [2828. T. Johannsen, Astrophys. J. 777, 170 (2013).], que por sua vez é uma função dos ângulos α e β, descritos na Fig. 4.
O ângulo sólido de um objeto, por exemplo um buraco negro, medido no referencial do observador, depende da distância entre os dois. Para medir a distância entre o objeto e o observador, utilizamos a definição do raio perimetral, que é um invariante geométrico, dado por [2727. P.V.P. Cunha e C.A.R. Herdeiro, Gen. Relativ. Grav. 50, 42 (2018)., 2929. P.V.P. Cunha, C.A.R. Herdeiro, E. Radu e H. Runarsson, Int. J. Mod. Phys. D 25, 1641021 (2016).]:
onde usamos que o integrando da Eq. (50) não depende da coordenada ϕ, o que está associado à simetria axial do espaço-tempo. O raio perimetral, que é calculado na coordenada radial do observador situado em r_0, é uma medida possível para a distância entre o centro do buraco negro e o observador. Os ângulos de observação (α, β) do buraco negro no referencial OMAN têm uma dependência no raio perimetral na forma de para observadores muito distantes do buraco negro. Isto implica que estes ângulos α e β são muito pequenos nesse limite.7 7 A partir da Terra, a abertura angular observada da região de emissão do disco de acreção no centro da galáxia M87 é de aproximadamente 42 milionésimos de segundo de arco (μ as) [10]. Neste regime, o par (x, y) pode ser escrito como8 8 Lançamos mão das aproximações cos(χ)≈1 e sin(χ)≈χ, quando o ângulo χ é muito pequeno.
Denotando por o tri-momento linear do fóton, i. e.
cuja norma é
podemos calcular suas componentes em função dos ângulos α e β, dadas por (ver Fig. 4):
Além disso, como fótons têm massa de repouso nula, i. e., Pμ = 0, logo P = p(t). Esta constante P não influencia na trajetória descrita por um fóton, e pode ser associada com a frequência deste, medida pelo observador.
Podemos escrever os ângulos α e β, presentes nas Eqs. (51) e (52), em termos das componentes do momento linear do fóton. Na aproximação de um observador muito distante do buraco negro, obtemos, das Eqs. (55) e (56), que:
Utilizando as Eqs. (46)–(49) nas Eqs. (58) e (59), e substituindo o resultado nas Eqs. (51)–(52), obtemos
onde θ0 determina a localização do observador na coordenada θ.
Para determinar a sombra de um buraco negro de Kerr, η e ξ presentes nas Eqs. (60)–(61) são interpretados matematicamente como funções paramétricas de r, determinadas pelas Eqs. (35)–(36). Para r ∈ [r1,r2], a sombra de um buraco negro de Kerr está apresentada na Fig. 5, para diferentes escolhas do parâmetro de rotação, vista por um observador no infinito e no plano equatorial.
Sombra de um buraco negro de Kerr descrita por um observador localizado muito distante do buraco negro () e no plano equatorial θ0 = π/2. Nesta figura escolhemos cinco valores para o parâmetro de rotação a do buraco negro.
Da Fig. 5, vemos que quanto mais próximo do valor de rotação máximo permitido para um buraco negro [ver Eq. (8)], mais assimétrica é a sombra de um buraco negro de Kerr. Para a = 0.999M, a sombra do buraco negro se assemelha com a forma da letra “D”.
Nas medidas obtidas pelo THE (cf. Fig. 1), o raio gravitacional do buraco negro supermassivo corresponde a uma escala angular de θg = 3.8 ± 0.4μas [1010. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L1 (2019)., 1414. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L5 (2019)., 1515. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L6 (2019).]. Como mencionamos anteriormente, este buraco negro, que está localizado no centro da galáxia Messier 87, possui uma massa estimada [1010. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L1 (2019).] de MBH = (6.5 ± 0.7)×109M⊙, onde M⊙ = 1,989×1030kg é a massa do Sol.
5. Tracejamento Inverso de Raios
Na seção 4 4. Sombras de Buracos Negros Observadores locais na geometria de Kerr Iniciamos esta seção tratando de um referencial ligado a um observador local na geometria de Kerr. Podemos descrever como este observador mede as componentes do quadri-momento de um determinado fóton, além de sua percepção visual da sombra de um buraco negro de Kerr. Restringimos a nossa análise à classe de observadores denominada OMAN, que é uma abreviatura para o termo “Observador com Momento Angular Nulo”6. Um OMAN é descrito pela seguinte base tétrada [27] (40) e ^ ( t ) = ζ ∂ t + γ ∂ ϕ , (41) e ^ ( r ) = 1 g r r ∂ r , (42) e ^ ( θ ) = 1 g θ θ ∂ θ , (43) e ^ ( ϕ ) = 1 g ϕ ϕ ∂ ϕ , onde (44) ζ ≡ g ϕ ϕ g t ϕ 2 - g t t g ϕ ϕ , (45) γ ≡ - g t ϕ g ϕ ϕ g ϕ ϕ g t ϕ 2 - g t t g ϕ ϕ . O vetor e^(t) está relacionado à quadri-velocidade deste observador, enquanto que os vetores (e^(r),e^(θ),e^(ϕ)), dados nas Eqs. (41)–(43), são as direções espaciais do sistema de referência do observador, conforme mostrado na Fig. 4. A medida da energia de um fóton no referencial de um OMAN é obtida projetando-se o quadri-momento deste fóton na direção e^(t), isto é: Figura 4 Representação da decomposição do momento linear de um fóton na base (e^(r), e^(θ), e^(φ)). Esta decomposição é feita em função dos ângulos (α, β), onde α é o ângulo formado entre o tri-momento linear P→ e o plano gerado pelos versores e^(r) e e^(φ) (plano e^(r)⟂e^(φ)), enquanto que β é o ângulo que a projeção vertical de P→ no plano e^(r)⟂e^(φ) faz com o versor e^(r). O buraco negro está representado pela esfera à direita. Imagem publicada originalmente na Ref. [29]. (46) p ( t ) = - e ^ ( t ) μ p μ = - ( ζ p t + γ p ϕ ) = ζ E - γ Φ . Também podemos calcular a projeção do quadri-momento de um fóton nas direções espaciais e^r, e^θ e e^ϕ. Estas quantidades são interpretadas como as componentes do momento linear do fóton, conforme medido pelo OMAN, que são dadas por: (47) p ( r ) = e ^ r μ p μ = p r g r r , (48) p ( θ ) = e ^ θ μ p μ = p θ g θ θ , (49) p ( ϕ ) = e ^ ϕ μ p μ = Φ g ϕ ϕ . Da Eq. (49), notamos que um fóton com momento angular nulo em relação a um observador estático no infinito (Φ = 0) também terá momento angular nulo em relação ao OMAN. Isto acontece porque a classe OMAN possui momento angular nulo em relação a um observador estático no infinito, como o próprio nome sugere. A Sombra de um Buraco Negro de Kerr O OMAN pode projetar os fótons recebidos em um determinado plano cartesiano. Podemos atribuir a cada fóton detectado no sistema de referência deste observador um par de coordenadas cartesianas (x, y). Estas coordenadas cartesianas definem o parâmetro de impacto de um fóton [28], que por sua vez é uma função dos ângulos α e β, descritos na Fig. 4. O ângulo sólido de um objeto, por exemplo um buraco negro, medido no referencial do observador, depende da distância entre os dois. Para medir a distância entre o objeto e o observador, utilizamos a definição do raio perimetral, que é um invariante geométrico, dado por [27, 29]: (50) r ~ ≡ 1 2 π ∫ 0 2 π g ϕ ϕ d ϕ | θ = π / 2 = g ϕ ϕ | θ = π / 2 , onde usamos que o integrando da Eq. (50) não depende da coordenada ϕ, o que está associado à simetria axial do espaço-tempo. O raio perimetral, que é calculado na coordenada radial do observador situado em r_0, é uma medida possível para a distância entre o centro do buraco negro e o observador. Os ângulos de observação (α, β) do buraco negro no referencial OMAN têm uma dependência no raio perimetral na forma de 1/r~ para observadores muito distantes do buraco negro. Isto implica que estes ângulos α e β são muito pequenos nesse limite.7 Neste regime, o par (x, y) pode ser escrito como8 (51) x ≈ - r ~ β , (52) y ≈ r ~ α . Denotando por P→ o tri-momento linear do fóton, i. e. (53) P → ≡ ( p ( r ) , p ( θ ) , p ( ϕ ) ) , cuja norma é (54) P 2 = ( p ( r ) ) 2 + ( p ( θ ) ) 2 + ( p ( ϕ ) ) 2 , podemos calcular suas componentes em função dos ângulos α e β, dadas por (ver Fig. 4): (55) p ( ϕ ) = P cos α sin β , (56) p ( θ ) = P sin α , (57) p ( r ) = P cos α cos β . Além disso, como fótons têm massa de repouso nula, i. e., Pμ = 0, logo P = p(t). Esta constante P não influencia na trajetória descrita por um fóton, e pode ser associada com a frequência deste, medida pelo observador. Podemos escrever os ângulos α e β, presentes nas Eqs. (51) e (52), em termos das componentes do momento linear do fóton. Na aproximação de um observador muito distante do buraco negro, obtemos, das Eqs. (55) e (56), que: (58) β ≈ p ( ϕ ) P = p ( ϕ ) p ( t ) , (59) α ≈ p ( θ ) P = p ( θ ) p ( t ) . Utilizando as Eqs. (46)–(49) nas Eqs. (58) e (59), e substituindo o resultado nas Eqs. (51)–(52), obtemos (60) x = - ξ sin θ 0 , (61) y = η + a 2 cos 2 θ 0 - ξ 2 tan 2 θ 0 , onde θ0 determina a localização do observador na coordenada θ. Para determinar a sombra de um buraco negro de Kerr, η e ξ presentes nas Eqs. (60)–(61) são interpretados matematicamente como funções paramétricas de r, determinadas pelas Eqs. (35)–(36). Para r ∈ [r1,r2], a sombra de um buraco negro de Kerr está apresentada na Fig. 5, para diferentes escolhas do parâmetro de rotação, vista por um observador no infinito e no plano equatorial. Figura 5 Sombra de um buraco negro de Kerr descrita por um observador localizado muito distante do buraco negro (r~≫M) e no plano equatorial θ0 = π/2. Nesta figura escolhemos cinco valores para o parâmetro de rotação a do buraco negro. Da Fig. 5, vemos que quanto mais próximo do valor de rotação máximo permitido para um buraco negro [ver Eq. (8)], mais assimétrica é a sombra de um buraco negro de Kerr. Para a = 0.999M, a sombra do buraco negro se assemelha com a forma da letra “D”. Nas medidas obtidas pelo THE (cf. Fig. 1), o raio gravitacional do buraco negro supermassivo corresponde a uma escala angular de θg = 3.8 ± 0.4μas [10, 14, 15]. Como mencionamos anteriormente, este buraco negro, que está localizado no centro da galáxia Messier 87, possui uma massa estimada [10] de MBH = (6.5 ± 0.7)×109M⊙, onde M⊙ = 1,989×1030kg é a massa do Sol. , vimos que é possível encontrar analiticamente a forma da sombra de um buraco negro de Kerr. Isto acontece devido às simetrias presentes neste espaço-tempo, codificadas na existência dos vetores de Killing nas direções t e ϕ, e na existência de um tensor de Killing não trivial Kμ ν, que dá origem à constante de Carter Q9 9 Se Kμ ν for um tensor de Killing, a quantidade Q=Kμνx.μx.ν é conservada ao longo de uma geodésica. . No entanto, um espaço-tempo genérico não possui uma constante de Carter, e como consequência não é possível encontrar a sombra de um buraco negro de maneira analítica. Um exemplo deste fato são os buracos negros de Kerr com cabelo escalar [3131. C.A.R. Herdeiro e E. Radu, Phys. Rev. Lett. 112, 221101 (2014).]. Nestas situações, podemos analisar as equações da geodésica, dadas por [33. M.P. Hobson, G.P. Efstathiou e A.N. Lasenby, General Relativity: an Introduction for Physicists (Cambridge University Press, Cambridge, 2006).]
Estas equações, que são válidas independentemente das simetrias do espaço-tempo, consistem em um sistema de equações diferenciais ordinárias com derivadas de segunda ordem em relação ao parâmetro afim τ.
Assumindo um espaço-tempo estacionário e com simetria axial, podemos escrever que
Com o intuito de determinar a sombra de um buraco negro estacionário e com simetria axial, usamos o método de tracejamento inverso de raios. Este método eficiente consiste em evoluir os raios de luz, a partir das coordenadas do observador, para trás no tempo e detetar a origem de cada raio de luz. Para integrar numericamente as Eqs. (63)–(66), precisamos impor condições iniciais. Visto que evoluímos os raios de luz para trás no tempo, as condições iniciais são dadas pelo quadri-vetor posição do fóton10 10 Que coincide com o quadri-vetor posição do observador. (t0, r0, θ0, ϕ0) e pelo quadri-momento do fóton na posição do observador, a saber:
onde utilizamos as Eqs. (46)–(49) e (55)–(57). Além das condições iniciais, devemos decidir quando terminar a integração numérica de um determinado raio de luz. Quando um raio de luz chega muito próximo do horizonte de eventos do buraco negro (r≈r+), interrompemos a integração numérica e consideramos este raio como sendo absorvido pelo buraco negro. Caso o raio de luz tenha coordenada radial muito maior que a do horizonte de eventos, por exemplo r≈30M, consideramos que este raio escapou da atração gravitacional do buraco negro, ou seja, é um caso de espalhamento, e interrompemos a integração numérica. Com o intuito de distinguir os raios espalhados dos raios absorvidos, supomos que há uma esfera celeste de raio r = 30M emitindo luz de maneira isotrópica. Podemos escolher um padrão para a esfera celeste, que destaque os efeitos de lentes gravitacionais. Este padrão depende somente das coordenadas (θ,ϕ). Na Fig. 6, adotamos um padrão do tipo “xadrez”, e mostramos a percepção visual de um observador no espaço-tempo de Minkowski (sem a presença de um buraco negro).
Percepção visual da esfera celeste, representada com um padrão tipo “xadrez”. Nesta imagem o observador está no espaço-tempo de Minkowski (sem a presença de um buraco negro).
Na presença de um buraco negro, descrito, por exemplo, pela métrica de Kerr, a percepção visual de um observador é, em geral, diferente de um espaço-tempo plano. Esta variação se deve não somente à presença da sombra do buraco negro, mas também devido aos efeitos de lente gravitacional. Na Fig. 7, exemplificamos a percepção visual de um observador na presença de um buraco negro de Kerr, utilizando o mesmo padrão da Fig. 6. Utilizamos o método de tracejamento inverso de raios para a métrica de Kerr com a=M, isto é, um buraco negro de Kerr extremo. Além disso, ressaltamos que nas Figs. 6 e 7 o observador está localizado no plano equatorial (θ0 = π/2) e possui raio perimetral .
Percepção visual de um observador nas mesmas condições que as da Fig. 6, porém na presença de um buraco negro. Para esta imagem utilizamos o método de tracejamento inverso de raios para um buraco negro de Kerr extremo (a = M).
Apesar de podermos estudar a sombra e o efeito de lente gravitacional do buraco negro de Kerr adotando o padrão “xadrez” para a esfera celeste, esta é uma configuração puramente acadêmica. Configurações astronômicas mais realistas levam em conta a presença de matéria ao redor do buraco negro, em particular discos de acreção. Estes discos são formados por matéria difusa orbitando o buraco negro. As primeiras simulações computacionais do aspecto visual de buracos negros com matéria ao redor foram feitas assumindo um disco de acreção fino orbitando um buraco negro de Schwarzschild [3232. J.P. Luminet, Astron. Astrophys. 75, 228 (1979).].
Podemos considerar outros modelos para descrever o disco de acreção. Neste trabalho, consideramos o modelo de Page-Thorne, que é um modelo idealizado de disco de acreção, onde as partículas que constituem o disco estão restritas a um movimento circular ao longo do plano equatorial [3333. D.N. Page e K.S. Thorne, The Astrophysical Journal 191, 499 (1974).]. Nas Figs. 8 e 9, apresentamos a sombra de buracos negros de Kerr com um disco de acreção de Page-Thorne. Para gerarmos as simulações exibidas nas Figs. 8 e 9, utilizamos o software GYOTO (General relativitY Orbit Tracer of Observatoire de Paris) [3434. F.H. Vincent, T. Paumard, E. Gourgoulhon e G. Perrin, Class. Quantum Gravity 28, 22 (2011).]. Este software contém suporte para tracejamento inverso de raios em vários espaços-tempos, dentre eles o espaço-tempo de Kerr. Além disso, o software GYOTO permite a simulação de vários objetos astrofísicos, por exemplo, buracos negros com disco de acreção de Page-Thorne11 11 Com conhecimentos básicos de linguagem de programação, o leitor pode gerar o tracejamento inverso de raios em algumas configurações pré-definidas, seguindo o manual do software disponível em [35]. .
Tracejamento inverso de raios no espaço-tempo de Kerr com um disco de acreção de Page-Thorne ao seu redor. O parâmetro de rotação do buraco negro foi fixado em a = 0.5M. O observador está localizado em θ0 = 85°, isto é, ligeiramente acima do plano equatorial.
Tracejamento inverso de raios no espaço-tempo de Kerr com um disco de acreção de Page-Thorne ao seu redor. Na imagem da esquerda representamos um buraco negro com parâmetro de rotação a = 0.94M, com o observador localizado em θ0 = 17°. Na imagem da direita aplicamos um filtro de desfocagem Gaussiano à imagem da esquerda, como uma tentativa simplificada de reproduzir as condições de observação do THE. De forma a obter uma melhor comparação com a imagem do THE exibida na Fig. 1, a orientação destas imagens foi modificada relativamente à da Fig. 8.
Na Fig. 8, escolhemos o parâmetro de rotação do buraco negro de Kerr como sendo a = 0.5M. O observador foi posicionado em θ0 = 85°, ou seja, ligeiramente fora do plano equatorial. Este observador consegue visualizar a parte que está “atrás” do buraco negro, devido aos efeitos de lente gravitacional que geram uma posição aparente de parte do disco de acreção acima do buraco negro. Curiosamente, há uma maior intensidade dos raios de luz no lado esquerdo da imagem, em comparação ao lado direito. Isto acontece devido à rotação do buraco negro e ao efeito Doppler e Liouville [55. C.W. Misner, K.S. Thorne e J.A. Wheeler, Gravitation (Freeman, San Francisco, 1973).]. O efeito Doppler consiste na mudança da frequência observada de uma onda quando há movimento relativo entre fonte e observador. Em particular, a análise do efeito Doppler em ondas eletromagnéticas nos permite inferir a velocidade de afastamento ou aproximação de estrelas e galáxias. Estas medidas tornaram possível, por exemplo, a descoberta da expansão do universo. Já o efeito Liouville é a mudança na intensidade de uma onda devido ao movimento relativo entre fonte e observador. Este fenômeno é consequência do teorema de Liouville sobre a conservação do volume no espaço de fase [2424. N.A. Lemos, Mecânica analítica (Editora Livraria da Física, São Paulo, 2007).].
De forma a fazer uma melhor comparação com a imagem de M87* obtida pelo THE, na Fig. 9 está representada a imagem de um buraco negro de Kerr com a = 0.94M, circundado por um disco de acreção de Page-Thorne, visto com um ângulo de θo = 17° (parâmetros correspondentes aos da imagem da Fig. 1). Uma vez que o THE tem uma resolução de observação limitada, também aplicamos um filtro Gaussiano de desfocagem sobre a imagem obtida pelo GYOTO. Este procedimento muito simplificado procura reproduzir a imagem obtida pelo THE. Podemos comparar o resultado desta simulação com a imagem observada pelo THE na Fig. 1, sendo notável a semelhança. Nas simulações publicadas pela colaboração internacional THE, considerou-se como modelo para o disco de acreção um gás a alta temperatura e magnetizado ao redor do buraco negro.
A obtenção da imagem da sombra de um buraco negro pelo THE, juntamente com as deteções de ondas gravitacionais [3636. B.P. Abbot, T.D. Abbott, M.R. Abernathy, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R.X. Adhikari, V.B. Adya et al., Phys. Rev. Lett. 116, 061102 (2016).], marcam o início das confirmações experimentais da gravitação em regime de campo forte, que estão consistentes com os resultados previstos pela TRG.
6. Conclusões
Neste trabalho analisamos as sombras de buracos negros de Kerr. Estas sombras são obtidas a partir do conjunto das órbitas esféricas de fótons presentes neste espaço-tempo.
Com as equações de movimento no espaço-tempo de Kerr, analisamos o movimento de fótons, que possuem massa de repouso nula. A partir disso, mostramos que existem órbitas cuja coordenada radial permanece constante, que são denominadas órbitas esféricas de fótons.
O conjunto das órbitas esféricas de fótons determina a sombra do buraco negro. Apresentamos a forma analítica da sombra de um buraco negro de Kerr, bem como seu aspecto visual, assim como visto por um observador distante. A forma da sombra do buraco negro de Kerr para valores de rotação muito baixo é aproximadamente circular. Conforme o parâmetro de rotação do buraco negro aumenta, a sombra se torna assimétrica. Para um buraco negro de Kerr extremo, temos uma sombra que se assemelha ao formato da letra “D”.
Também discutimos o método de tracejamento inverso de raios, que consiste em resolver numericamente as equações da geodésica com a finalidade de obter uma imagem da sombra de um buraco negro. Este método é particularmente importante quando não é possível determinar a forma analítica da sombra de um buraco negro. Primeiramente, consideramos apenas o buraco negro com a esfera celeste ao seu redor. Nesta esfera celeste adotou-se um padrão regular tipo “xadrez”, que depende das coordenadas (θ,ϕ). Desta forma, obtivemos a percepção visual de um observador ao redor deste buraco negro, isto é, o formato da sombra e os efeitos de lente gravitacional. Como uma ilustração adicional, na Fig. 10 o padrão da esfera celeste foi substituído pelo símbolo da Revista Brasileira de Ensino de Física.
Tracejamento inverso de raios utilizando o símbolo da Revista Brasileira de Ensino de Física como padrão para a esfera celeste. Nesta figura, temos um buraco negro de Kerr extremo (a=M), o observador está localizado no plano equatorial com coordenada radial r0 = 10M e a esfera celeste tem raio 20M.
Para descrever situações astronômicas mais realistas, ilustramos o método de tracejamento inverso de raios para um buraco negro de Kerr com um disco de acreção. Este disco de acreção foi descrito pelo modelo de Page-Thorne. Nesta configuração mais próxima dos casos astrofísicos, vários fenômenos interessantes podem ser constatados. Por exemplo, a possibilidade de o observador ver “a parte de trás” do disco de acreção, devido aos efeitos de lente gravitacional, e a diferença de intensidade dos raios de luz provenientes do disco de acreção, causada por efeitos Doppler e Liouville.
Agradecimentos
Gostaríamos de agradecer o apoio do Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), e do programa Horizon 2020 da União Europeia, sob o subsídio N° H2020-MSCA-RISE-2017 FunFiCO-777740. Agradecemos ainda o apoio da Fundação para a Ciência e a Tecnologia (FCT, Portugal) através dos projetos PTDC/FIS-OUT/28407/2017 e CERN/FIS-PAR/0027/2019. P.C. é apoiado pelo Max Planck Gesellschaft por meio do grupo “Gravitation and Black Hole Theory Independent Research Group”.
Referências
-
1.R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984).
-
2.S. Carroll, Spacetime and Geometry (Addison Wesley, San Francisco, 2004).
-
3.M.P. Hobson, G.P. Efstathiou e A.N. Lasenby, General Relativity: an Introduction for Physicists (Cambridge University Press, Cambridge, 2006).
-
4.R. D’Inverno, Introducing Einstein’s Relativity (Clarendon Press, Oxford, 1992).
-
5.C.W. Misner, K.S. Thorne e J.A. Wheeler, Gravitation (Freeman, San Francisco, 1973).
-
6.J.A. Wheeler e K. Ford, Geons, Black Holes and Quantum Foam: A life in Physics (WW Norton, Nova York, 1998).
-
7.A. Saa, Rev. Bras. Ensino Fís. 38 , e4201 (2016).
-
8.J.P.B. Brito, R.P. Bernar, C.L. Benone e L.C.B. Crispino, Rev. Bras. Ensino Fís. 42, e20200015 (2020).
-
9.R.P. Kerr, Phys. Rev. Lett. 11, 237 (1963).
-
10.The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L1 (2019).
-
11.The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L2 (2019).
-
12.The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L3 (2019).
-
13.The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L4 (2019).
-
14.The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L5 (2019).
-
15.The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L6 (2019).
-
16.https://eventhorizontelescope.org
» https://eventhorizontelescope.org -
17.http://www.robgendlerastropics.com
» http://www.robgendlerastropics.com -
18.F.W. Dyson, A.S. Eddington e C. Davidson, Philos. Trans. R. Soc. Lond. A 220, 291 (1920).
-
19.L.C.B. Crispino e M.C. Lima, Rev. Bras. Ens. Fís. 38, e4203 (2016).
-
20.L.C.B. Crispino e D.J. Kennefick, Nat. Phys. 15, 416 (2019).
-
21.S.V.C.B. Xavier, L.C.S. Leite, C.L. Benone, C.A.R. Herdeiro e L.C.B. Crispino, Rev. Bras. Ens. Fís. 42, e20200181 (2020).
-
22.B. Carter, Phys. Rev. 174, 1559 (1968).
-
23.D.C. Wilkins, Phys. Rev. D. 5, 814 (1972).
-
24.N.A. Lemos, Mecânica analítica (Editora Livraria da Física, São Paulo, 2007).
-
25.E. Teo, Gen. Relativ. Gravit. 35, 1909 (2003).
-
26.P.V.P. Cunha e C.A.R. Herdeiro, Phys. Rev. Lett. 124, 181191 (2020).
-
27.P.V.P. Cunha e C.A.R. Herdeiro, Gen. Relativ. Grav. 50, 42 (2018).
-
28.T. Johannsen, Astrophys. J. 777, 170 (2013).
-
29.P.V.P. Cunha, C.A.R. Herdeiro, E. Radu e H. Runarsson, Int. J. Mod. Phys. D 25, 1641021 (2016).
-
30.J.M. Bardeen, em Black holes, editado por C. DeWitt e B.S. DeWitt (Ecole d’été de physique théorique, Les Houches, 1972).
-
31.C.A.R. Herdeiro e E. Radu, Phys. Rev. Lett. 112, 221101 (2014).
-
32.J.P. Luminet, Astron. Astrophys. 75, 228 (1979).
-
33.D.N. Page e K.S. Thorne, The Astrophysical Journal 191, 499 (1974).
-
34.F.H. Vincent, T. Paumard, E. Gourgoulhon e G. Perrin, Class. Quantum Gravity 28, 22 (2011).
-
35.https://gyoto.obspm.fr/GyotoManual.pdf
» https://gyoto.obspm.fr/GyotoManual.pdf -
36.B.P. Abbot, T.D. Abbott, M.R. Abernathy, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R.X. Adhikari, V.B. Adya et al., Phys. Rev. Lett. 116, 061102 (2016).
-
1
Uma tradução para o português é: “O espaço-tempo diz à matéria como se mover; a matéria diz ao espaço-tempo como se encurvar”.
-
2
Vetores e tensores de Killing indicam as direções nas quais o espaço-tempo possui simetria. Por exemplo, um espaço-tempo que possui simetria de translação temporal, admite um vetor de Killing na direção da coordenada temporal, o que acontece, por exemplo, na geometria de Minkowski. A existência de um vetor de Killing está também associada à conservação de uma grandeza ao longo de um movimento geodésico.
-
3
Tradução do termo em inglês “Backwards ray-tracing”.
-
4
As coordenadas de Boyer-Lindquist são coordenadas do tipo esferoidais oblatas e são úteis para tratar diversos aspectos do espaço-tempo de Kerr como, por exemplo, o estudo de geodésicas nulas. Nestas coordenadas, o único termo não-diagonal é gt ϕ, que é responsável por efeitos interessantes na métrica de Kerr, como é o caso do arrasto dos referenciais inerciais, que ocorre quando um referencial inercial é arrastado no mesmo sentido de rotação do buraco negro.
- 5
-
6
A abreviatura correspondente em inglês é ZAMO, correspondendo ao termo “Zero Angular Momentum Observer”.
-
7
A partir da Terra, a abertura angular observada da região de emissão do disco de acreção no centro da galáxia M87 é de aproximadamente 42 milionésimos de segundo de arco (μ as) [1010. The event Horizon Telescope Collaboration, Astrophys. J. Lett. 875, L1 (2019).].
-
8
Lançamos mão das aproximações cos(χ)≈1 e sin(χ)≈χ, quando o ângulo χ é muito pequeno.
-
9
Se Kμ ν for um tensor de Killing, a quantidade é conservada ao longo de uma geodésica.
-
10
Que coincide com o quadri-vetor posição do observador.
-
11
Com conhecimentos básicos de linguagem de programação, o leitor pode gerar o tracejamento inverso de raios em algumas configurações pré-definidas, seguindo o manual do software disponível em [3535. https://gyoto.obspm.fr/GyotoManual.pdf.
https://gyoto.obspm.fr/GyotoManual.pdf... ].
Datas de Publicação
-
Publicação nesta coleção
04 Dez 2020 -
Data do Fascículo
2021
Histórico
-
Recebido
01 Jun 2020 -
Revisado
19 Out 2020 -
Aceito
23 Out 2020