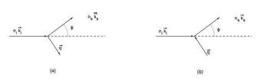Lei da reflexão, lei de Snell e efeito Goos-Hänchen: abordagem via modelo corpuscular da luz

Law of reflection, Snell’s law and the Goos-Hänchen effect: an approach from a corpuscular model of light

Resumos

Usamos as leis de conservação de energia e momento linear no contexto do modelo corpuscular da luz de Einstein para obter as leis de reflexão e refração da óptica geométrica. Adicionalmente o efeito Goos-Hänchen é abordado e o deslocamento lateral da luz refletida é calculado.

Palavras-chave
Lei da reflexão; Lei de Snell; Efeito Goos-Hänchen; Modelo corpuscular da luz

In this article we use Einstein’s model that treats light in its corpuscular behavior to determine the laws of reflection and refraction. For total internal reflection we predict the Goos-Hanchen shift.

Keywords
Law of reflection; Snell’s law; Goos-Hänchen effect; Corpuscular model of light

1. Introdução

Quando um feixe de luz incide sobre uma interface que separa dois meios homogêneos e transparentes, parte da luz incidente é refletida e parte é refratada (ou transmitida) para o segundo meio, originando o feixe refratado, conforme esquematizado na Figura 1. Do ponto de vista da óptica geométrica, esse fenômeno é descrito pelas leis da reflexão e refração. A lei da reflexão afirma que o raio incidente, o raio refletido e a normal à superfície pertencem a um mesmo plano e que o ângulo de incidência, θ_i, é igual ao ângulo de reflexão, θ_r, medidos em relação à perpendicular ao plano de separação entre os dois meios, i.e.,

Figura 1
Interface plana entre dois meios opticamente distintos. O raio incidente dá origem a um raio refletido e a um raio transmitido.

(1) $${\theta }_i={\theta }_r$$

A lei da refração estabelece que o raio refratado, o raio incidente e a normal à superfície pertencem ao mesmo plano e que o ângulo de incidência e o ângulo de refração, θ_t, estão relacionados pela expressão

(2) $$n_i\sin {\theta }_i=n_t\sin {\theta }_t$$

onde n_i e n_t são os índices de refração dos meios incidente e transmitido, respectivamente. Essa lei foi descoberta em 1621 pelo holandês Villebrord Snell e independentemente pelo filósofo e matemático francês René Descartes.

Essas leis podem ser deduzidas por diferentes métodos. Por exemplo, via princípio de Huygens ou princípio de Fermat [¹, ²]. Contudo, esses princípios não são capazes de calcular como a energia da onda incidente se reparte entre as ondas refletida e transmitida. A resposta a essa questão é fornecida pela teoria eletromagnética da luz, a qual permite calcular a refletividade (fração da potência incidente que é refletida) e a transmissividade (fração da potência incidente que é transmitida). No contexto dessa teoria, para se deduzir as leis da reflexão e refração é necessário determinar o campo eletromagnético na interface que separa os dois meios; isso é realizado utilizando as denominadas condições de contorno sobre o campo eletromagnético [¹]. Adicionalmente, é possível, via teoria eletromagnética, concluir que as frequências da onda incidente, ω_i, da onda refletida, ω_r, e da onda transmitida, ω_t, são iguais:

(3) $${\omega }_i={\omega }_r={\omega }_t$$

Apesar de serem leis bem estabelecidas e já amplamente incorporadas nos livros didáticos, é interessante observar a existência de trabalhos relativamente recentes que procuram novas formulações para expressar as leis da reflexão e da refração. Nas referências [³] e [⁴], por exemplo, as leis da reflexão e refração são apresentadas de maneira reformuladas, permitindo a abordagem de alguns problemas da óptica geométrica de modo mais simples e intuitivo.

No presente estudo vamos analisar o comportamento da luz em uma interface dielétrica que separa dois meios homogêneos distintos, utilizando o modelo corpuscular da luz de Einstein. Segundo esse modelo, a radiação eletromagnética é formada por um conjunto de partículas indivisíveis (os fótons) que carregam energia ℏω e momento linear de magnitude ℏω/c, onde ℏ = h/2π e h é a constante de Planck e ω a frequência angular da radiação. Vamos considerar os fenômenos de reflexão e refração como processos de espalhamento de um fóton no qual há conservação de energia e de momento linear do sistema. Mostraremos que as leis da reflexão e refração da óptica geométrica são verificadas quando o espalhamento do fóton é elástico. Veremos que para que haja conservação do momento linear faz-se necessário a criação ou aniquilação de uma quasipartícula no sistema. Veremos também que a partir desse modelo é possível obter uma explicação qualitativa para a existência do efeito Goos-Hänchen para reflexão interna total.

2. Leis de Conservação Para o Espalhamento do Fóton

Da teoria da relatividade restrita sabemos que a energia, E, e o momento linear de uma partícula se relacionam por meio da equação:

(4) $$E=\sqrt{{(pc)}^2+{(m_0{c}^2)}^2}$$

onde p é a magnitude do momento linear da partícula, m₀ é a massa de repouso da partícula e c a velocidade da luz no vácuo. Como a massa de repouso do fóton é nula temos que:

(5) $$p=\frac{E}{c}=\frac{\mathrm{\hslash }\omega }{c}=\mathrm{\hslash }k$$

onde k = ω/c é a magnitude do vetor de onda no vácuo. Essas ideias acerca das propriedades corpusculares da luz foram confirmadas via efeito Compton [⁵], onde foi mostrado Raios-X (antes considerado apenas como ondas eletromagnéticas) tendo comportamento corpuscular.

Para um meio material, sabemos que a velocidade da luz¹ é dada como v = c/n. Desse modo, o valor do vetor de onda do fóton no material deve diferir do seu valor no vácuo por um fator igual ao índice de refração da luz no meio. Assim, a equação (5) torna-se, na forma vetorial:

(6) $$\overrightarrow{p}=\mathrm{\hslash }n\overrightarrow{k}$$

No processo de espalhamento do fóton incidente, além do fóton espalhado (refletido ou transmitido), há a criação ou aniquilação de uma quasipartícula (ou excitação elementar). De forma simplificada, podemos definir quasipartícula como uma partícula fictícia que descreve de forma relativamente simples o comportamento de sistemas de muitos corpos [⁶, ⁷].

Consideremos um fóton incidente de energia ℏω_i e momento linear $\mathrm{\hslash }{n}_i\overrightarrow{k_i}$. Devido a colisão com a superfície, resulta um fóton espalhado de energia ℏω_s e momento linear $\mathrm{\hslash }{n}_s\overrightarrow{k_s}$, onde ω_s = ω_r, n_s = n_r e $\overrightarrow{k_s}=\overrightarrow{k_r}$ (para o fóton refletido) ou ω_s = ω_t, n_s = n_t e $\overrightarrow{k_s}=\overrightarrow{k_t}$ (para o fóton transmitido). As leis de conservação da energia e do momento linear são expressas como:

(7) $$\mathrm{\hslash }{\omega }_i=\mathrm{\hslash }{\omega }_s\pm \mathrm{\hslash }{\omega }_q$$

(8) $$\mathrm{\hslash }{n}_i{\overrightarrow{k}}_i=\mathrm{\hslash }{n}_s{\overrightarrow{k}}_s\pm \mathrm{\hslash }\overrightarrow{q}$$

onde ℏω_q ($\mathrm{\hslash }\overrightarrow{q}$) é a energia (momento linear) da quasipartícula criada ou aniquilada no processo de espalhamento do fóton incidente. O sinal (+) se refere a um processo no qual uma quasipartícula é criada, conhecido como componente Stokes, Figura 2(a). No caso de aniquilação, sinal (−), trata-se do componente Anti-Stokes, Figura 2(b).

Figura 2
Espalhamento de um fóton através de um ângulo ϕ com a criação de uma quasipartícula (a), processo Stokes, e (b) aniquilação de uma quasipartícula, processo anti-Stokes.

Da própria noção de fóton, que implica em sua indivisibilidade, o fóton incidente será refletido ou será refratado (transmitido), ou seja, não é possível um mesmo fóton ser simultaneamente refletido e transmitido. O que explica se o fóton incidente será refletido ou transmitido é a teoria quântica da luz, a qual permite calcular a probabilidade de reflexão ou transmissão.

3. Leis da Reflexão e Refração Via Modelo Corpuscular

Mostraremos agora que é possível obter as leis de reflexão e refração da óptica geométrica, equações (1) e (2), a partir das leis de conservação expressas pelas equações (7) e (8). Um fóton incidente de energia ℏω_i e momento linear $\mathrm{\hslash }{n}_i\overrightarrow{k_i}$ dará origem ou a um fóton refletido (de energia ℏω_r e momento linear $\mathrm{\hslash }{n}_r\overrightarrow{k_r}$, Figura 3(a)) ou a um fóton transmitido (de energia ℏω_t e momento linear $\mathrm{\hslash }{n}_r\overrightarrow{k_t}$, Figura 3(b)).

Figura 3
Colisão entre um fóton e superfície, havendo conservação do momento linear do fóton na direção do eixo x, gerando o fenômeno de reflexão (a), (b) refração.

Devido a invariância translacional na direção paralela a interface (eixo x), a componente longitudinal do momento linear do fóton se conserva. Podemos expressar matematicamente essa invariância como

(9) $$n_i|\overrightarrow{k_i}\times \widehat{N}|=n_r|\overrightarrow{k_r}\times \widehat{N}|$$

para o fóton refletido e

(10) $$n_i|\overrightarrow{k_i}\times \widehat{N}|=n_t|\overrightarrow{k_t}\times \widehat{N}|$$

para o fóton transmitido, onde $\widehat{N}$ é um versor normal à superfície que aponta do meio incidente para o meio transmitido. Em termos dos ângulos de incidência, reflexão e refração as equações (9) e (10) ficam

(11) $${\omega }_i\sin {\theta }_i={\omega }_r\sin {\theta }_r$$

(12) $$n_i{\omega }_i\sin {\theta }_i=n_t{\omega }_t\sin {\theta }_t$$

onde usamos que n_i = n_r na equação (11). Supondo um espalhamento elástico, ω_i = ω_r = ω_t obtemos da equação (11) a lei da reflexão, θ_i = θ_r, e da equação (12) a lei de Snell, n_isin⁡θ_i = n_tsin⁡θ_t. Vemos, então, que as leis de reflexão e refração da óptica geométrica são consequências da conservação do componente longitudinal do momento linear do fóton e do fato do espalhamento ser elástico.

Como podemos conciliar o espalhamento elástico da luz com a equação (7)? Para um sólido, geralmente a energia da quasipartícula é muito menor que a energia do fóton espalhado. Os fótons correspondentes à faixa do visível do espectro eletromagnético possuem energia no intervalo de 1, 7 a 3, 1 eV. Por sua vez, a energia dos fônons óticos, por exemplo, está na faixa de 10 meV a 0, 2 eV. Assim, considerando que ω_q≈0, podemos afirmar que o espalhamento será elástico, conhecido também como espalhamento Rayleigh, efeito responsável pela cor azul do céu [⁸]. Nesse caso, as frequência das luzes incidente, refletida e transmitida são iguais, que é o conhecido resultado da óptica física, equação (3).

É interessante observar que mesmo considerando um espalhamento elástico, ω_q≈0, a lei da conservação do momento linear, equação (8), exige que o momento linear da quasipartícula não seja nulo. As implicações físicas desse fato serão exploradas na próxima Seção.

4. Momento Linear da Quasipartícula

Vimos na Seção anterior que a componente longitudinal do momento linear do fóton se conserva. Isso significa que o vetor de onda $\overrightarrow{q}$ da quasipartícula só tem componente normal a interface, i.e., $\overrightarrow{q}=q\widehat{y}$. Vamos agora analisar o comportamento de q. Trataremos separadamente os casos de reflexão e refração do fóton.

4.1. Espalhamento por reflexão

Se o fóton espalhado é o fóton refletido, para que ocorra a conservação do momento linear do sistema, deve haver a criação de uma quasipartícula (processo Stokes). A componente y da equação (8) pode ser escrita como

(13) $$n_i{k}_i\cos {\theta }_i=-n_r{k}_r\cos {\theta }_r+q$$

Como n_i = n_r e k_i = k_r (espalhamento elástico), da equação (13) obtemos que

(14) $$q=2n_i{k}_i\cos ({\theta }_i)=2n_i{k}_{iy}$$

Vemos que o momento linear da quasipartícula é igual a duas vezes a componente normal do vetor de onda incidente. Esse resultado é esperado já que numa colisão elástica a componente vertical do momento linear da partícula é invertida.

4.2. Espalhamento por refração

A componente normal do momento do fóton transmitido pode ser maior ou menor que a mesma do incidente. O primeiro caso acontece quando n_i < n_t e o segundo quando n_i > n_t, como podemos perceber pela conservação do momento linear na equação (8). Por isso, analisaremos as duas situações separadamente.

Caso 1 – Passagem da luz de um meio menos refrigente para um mais refrigente, n_i < n_t.

Como o momento linear do fóton transmitido é maior que o do incidente, ℏn_tk_t > ℏn_ik_i, o processo é anti-Stokes, ou seja, uma quasipartícula é aniquilada. Nesse caso, pela equação (8), temos que:

(15) $$n_i{k}_i\cos ({\theta }_i)=n_t{k}_t\cos ({\theta }_t)-q$$

Da lei de Snell, temos que:

(16) $$\cos ({\theta }_t)=\sqrt{1-{\left(\frac{n_i}{n_t}\right)}^2{\sin }^2({\theta }_i)}$$

Usando essa relação e o fato que k_i = k_t na colisão elástica, obtemos da equação (15)

(17) $$q=n_i{k}_i\left[\left(\frac{n_t}{n_i}\right)\sqrt{1-{\left(\frac{n_i}{n_t}\right)}^2{\sin }^2({\theta }_i)}-\cos ({\theta }_i)\right]$$

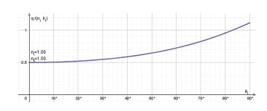
A Figura 4 mostra o gráfico de q/(n_ik_i) em função do ângulo de incidência para uma interface ar-vidro. Vemos que, para um k_i fixo, o número de onda q tem seu valor mínimo para incidência perpendicular, θ_i = 0, e seu valor máximo para incidência rasante, θ_i = 90°, crescendo monotonicamente entre os extremos.

Figura 4
Gráfico da equação (17).

Caso 2 – Passagem da luz de um meio mais refrigente para um menos refrigente, n_i > n_t.

Neste caso, há a criação de uma excitação elementar, p_t < p_i, isto é, uma quasipartícula é criada, que é o processo Stokes. Portanto, pela equação (8), temos que

(18) $$n_i{k}_i\cos ({\theta }_i)=n_t{k}_t\cos ({\theta }_t)+q$$

De modo semelhante ao caso 1, temos o mesmo acontecimento para os dois tipos de espalhamento. No elástico, usando a equação (16) na equação (18), encontramos que

(19) $$n_i{k}_i\cos ({\theta }_i)=n_t{k}_t\sqrt{1-{\left(\frac{n_i}{n_t}\right)}^2{\sin }^2({\theta }_i)}+q$$

Sabendo que k_i = k_t, pois a colisão é elástica, temos que:

(20) $$q=n_i{k}_i\left[\cos ({\theta }_i)-\left(\frac{n_t}{n_i}\right)\sqrt{1-{\left(\frac{n_i}{n_t}\right)}^2{\sin }^2({\theta }_i)}\right]$$

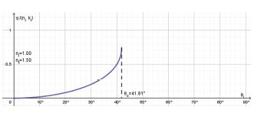
O valor de θ_i que anula o radicando da equação (20) é o ângulo crítico da reflexão total da óptica geométrica, i.e., sin⁡(θ_c) = n_t/n_i, como ilustra a Figura 5. Então, deve-se distinguir duas situações: a primeira é quando (n_i/n_t)²sin²⁡(θ_i)≤1, isto é, θ_i≤θ_c, caso em que a componente normal de k_t é real; a segunda é quando há reflexão total (n_i/n_t)²sin²⁡(θ_i) > 1, ou seja θ_i > θ_c, nesse caso a componente normal de k_t é imaginária.

Figura 5
Gráfico da equação (20).

Vamos discutir agora um resultado aparentemente contraditório. A antiga teoria corpuscular da luz, que remete à Newton, apresentava o seguinte ponto fraco: de acordo com esse modelo, é possível prever que a velocidade da luz seria maior em um meio mais refrigente do que em um meio menos refrigente, ou seja, a velocidade da luz seria maior no vidro do que no ar, por exemplo. Contudo, desde 1850 com o experimento de Foucault sabe-se que a velocidade da luz é menor em meios mais refrigentes. Mas, conforme vimos acima, a magnitude do momento linear do fóton é sempre maior em um meio mais refrigente. Como pode o fóton ter momento linear maior em um meio mais refrigente e sua velocidade ser menor nesse meio? Da equações (5) e (6) temos que para o fóton incidente p_iv_i = ℏω_i e igualmente para o fóton transmitido temos que p_tv_t = ℏω_t. Para espalhamento elástico, ω_i = ω_t, obtemos que p_iv_i = p_tv_t. Então vemos que no meio em que o fóton tem maior momento linear, a velocidade da luz será menor nesse meio.

5. O Modelo Corpuscular da Luz e o Efeito Goos-Hänchen

Veremos agora que o modelo corpuscular da luz aqui desenvolvido permite uma interpretação física do efeito Goos-Hänchen. Esse efeito consiste em um deslocamento lateral da luz refletida quando há reflexão interna total, ou seja, o feixe de luz refletido é deslocado do caminho ideal previsto pela óptica geométrica, conforme esquematizado na Figura 6. Tipicamente esse deslocamento é da ordem do comprimento de onda da luz, por isso não é facilmente observável. O primeiro a conjecturar a existência desse deslocamento foi Isaac Newton ainda no século XVIII. Contudo, a verificação experimental do efeito só foi realizada em 1947 por Hermann Goos e Hilda Hänchen [⁹]. Logo após o trabalho de Goos e Hänchen, Kurt Artmann apresentou uma explicação teórica para o fenômeno [¹⁰]. Utilizando o método da fase estacionária, Artmann conseguiu explicar o deslocamento observado bem como deduziu duas expressões para esse deslocamento que dependia da polarização da luz: uma expressão para a polarização paralela ao plano de incidência e outra expressão para a polarização perpendicular ao plano de incidência, que possuem as seguintes formas [¹¹].

Figura 6
Diagrama do efeito Goos-Hänchen onde é mostrado o raio refletido deslocado (linha cheia) de uma distância D em relação à situação descrita pela óptica geométrica (linha pontilhada).

(21) $$D_{\perp }=\frac{\lambda }{\pi }\frac{\sin {\theta }_i}{\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_t}{n_i}\right)}^2}}$$

(22) $$D_{\parallel }=D_{\perp }\frac{{\left(\frac{n_t}{n_i}\right)}^2}{{\sin }^2{\theta }_i-{\cos }^2{\theta }_i{\left(\frac{n_t}{n_i}\right)}^2}$$

Em novos experimentos realizados em 1949, Goos e Hänchen confirmaram a dependência do deslocamento lateral do estado de polarização da luz. Quando a luz incidente é circularmente polarizada, o deslocamento da luz refletida é transversal, i.e., perpendicular ao plano de incidência. Neste caso falamos de efeito Imbert-Fedorov, em homenagem a Fedor Fedorov, que previu o fenômeno em 1955, e a Christian Imbert, que o comprovou experimentalmente em 1972.

Para nossa análise vamos considerar o componente normal de k_t que é dado por

(23) $$k_{ty}=k_t\sqrt{1-{\left(n_i/n_t\right)}^2{\sin }^2{\theta }_i}$$

Vemos que k_ty diminui com o aumento do ângulo de incidência e se anula quando θ_i = θ_c. Para valores de ângulos de incidência maiores que o ângulo crítico, θ_i > θ_c, o componente normal de k_t torna-se imaginário. Sabemos da óptica física que um vetor de onda imaginário representa uma onda evanescente. Portanto, k_t imaginário é o vetor de onda do fóton associado à onda eletromagnética evanescente da reflexão total frustrada. Tem-se então uma interpretação corpuscular para esse fenômeno.

O número de onda imaginário k_ty pode ser escrito, para θ_i > θ_c, como

(24) $$k_{ty}=i|k_{ty}|$$

sendo i a unidade imaginária e

(25) $$|k_{ty}|=k_t\sqrt{{\left(n_i/n_t\right)}^2{\sin }^2{\theta }_i-1}$$

Pela associação de k_ty com a onda evanescente podemos definir uma profundidade de penetração do fóton transmitido da seguinte forma

(26) $$d=\frac{1}{n_t|k_{t}y|}$$

Podemos visualizar esse processo ótico como análogo ao processo quântico de penetração de barreira em um potencial degrau no qual a energia total da partícula é menor que a altura do degrau. Embora o coeficiente de reflexão (a refletividade) da partícula nesse caso seja igual a um, a probabilidade de encontrar a partícula na região classicamente proibida não é nula, ou seja, ocorre alguma penetração nessa região apesar da densidade de probabilidade decrescer exponencialmente com o aumento da distância [¹²]. Esse fenômeno é conhecido como penetração de barreira ou tunelamento [¹³]. De forma semelhante, para θ_i > θ_c, a probabilidade do fóton transmitido retornar para o meio incidente é igual a 1, mas ele não retorna exatamente da interface; ele penetra, em média, um distância d no meio transmitido antes de retornar ao meio refletido. Isso explica o deslocamento de Goos-Hänchen. Também temos que para θ_i > θ_c a probabilidade do fóton incidente ser refletido é muito maior do que ser transmitido e isso explica porque o deslocamento de Goos-Hänchen não é facilmente observável.

A profundidade de penetração d está relacionada com o deslocamento D de Goos-Hänchen pela expressão D = dsin⁡(θ_i), como ilustra a Figura 7. Usando essa expressão e as equações (25) e (26), obtemos

Figura 7
Relação entre o deslocamento de Goos-Hänchen D e a profundidade de penetração d. O deslocamento D é o cateto oposto do ângulo θ_i do triângulo retângulo de hipotenusa d.

(27) $$D=\frac{\sin ({\theta }_i)}{k_i\sqrt{{\sin }^2({\theta }_i)-{\left(n_t/n_i\right)}^2}}$$

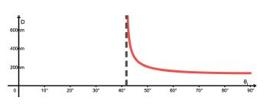
A equação (27), a menos de um fator 1/2, é igual a expressão obtida por Artman [⁷] para o caso de polarização perpendicular ao plano de incidência. Vemos que D tende a infinito quando o ângulo θ_i se aproxima do ângulo crítico θ_c = arcsin⁡(n_t/n_i). No modelo corpuscular, essa divergência significa que o fóton transmitido percorreria uma distância infinita no meio transmitido antes de retornar ao meio incidente.

A Figura 8 mostra o gráfico do deslocamento D em função do ângulo de incidência θ_i para uma interface ar-vidro e para um comprimento de onda da luz incidente de λ = 633 nm. A linha tracejada vertical indica a posição do ângulo crítico.

Figura 8
Deslocamento de Goos-Hänchen em função do ângulo de incidência.

6. Conclusão

Os fenômenos de reflexão e refração, apesar de sua aparente simplicidade, são manifestações macroscópicas de sutis processos de espalhamento que ocorrem em nível microscópico. De um ponto de vista fundamental, eles são determinados pelas propriedades eletrônicas e vibracionais do material no qual a luz incide. Neste trabalho utilizamos o modelo corpuscular da luz de Einstein para analisar os fenômenos de reflexão e refração que ocorrem em uma interface plana que separa dois meios homogêneos. Tomamos como ponto de partida as leis de conservação da energia e do momento linear no processo de espalhamento do fóton, equações (7) e (8). Vimos que para que se verifique a conservação dessas leis, junto com o espalhamento do fóton deve ocorrer a criação ou aniquilação de uma quasipartícula no sistema. Em geral, a energia dessa quasipartícula é muito menor que a energia dos fótons no visível, de modo que podemos considerar o espalhamento como elástico. Nesse caso, vemos imediatamente da relação E = ℏω que as frequências da luz refletida e refratada são iguais a frequência da luz incidente, um resultado que é obtido via teoria eletromagnética. Usando esse resultado e o fato de que a componente longitudinal do fóton incidente é igual a componente longitudinal do fóton espalhado, deduzimos a lei da reflexão e a lei da refração (lei de Snell) da óptica geométrica. A utilização do modelo corpuscular da luz para deduzir as leis da óptica geométrica é conhecida [¹⁴]. No presente trabalho, exploramos o fato de que é necessário a criação (ou aniquilação) de uma quasipartícula para que a conservação do momento linear do sistema seja obedecida. Adicionalmente, como um importante resultado, obtivemos de forma relativamente simples uma expressão para o deslocamento de Goos-Hänchen em torno do ângulo crítico para reflexão interna total, a qual, a menos de um fator 1/2, coincide com a expressão da óptica física para o estado de polarização perpendicular ao plano de incidência.

References

• ^1.
  E. Hecht, Optics (Addison-Wesley, Reading, Massachussetts, 2000).
• ^2.
  H. Moysés Nussenzveig, Curso de Física, Ótica, Relatividade e Fîsica Quântica (Editora Edgar Blücher, São Paulo, 1998), v. 4, 1ª ed.
• ^3.
  A.L. Pérez-Rodríguez, G. Martinez-Borreguero e M.I. Suero López, Revista Brasileira de Ensino de Física 39, e2404 (2017).
• ^4.
  G. Martinez-Borreguero, A.L Pérez-Rodríguez, M.I. Suero-López e F.L. Naranjo Correa, Revista Brasileira de Ensino de Física 36, e3401 (2018).
• ^5.
  I. Silva e O. Freire Jr., Revista Brasileira de Ensino de Física 39, 1601 (2014).
• ^6.
  A.V. Andrade-Neto, A. Ribeiro Neto e A. Jorio, Revista Brasileira de Ensino de Física 39, e3310 (2017).
• ^7.
  R.D. Mattuck, A Guide to Feynman Diagrams in the Many-body Problem (McGrawHill, New York, 1967).
• ^8.
  A.V. Andrade-Neto, B.P. Carneiro e M. Paixão, Física na Escola 17, 24 (2019).
• ^9.
  F. Goos e H. Hänchen, Ann. Physik 1, 333 (1947).
• ^10.
  K. Artmann, Annalen der Physik, 437, 87 (1948).
• ^11.
  J.D. Jackson, Classical Electrodynamics (John Wiley, New York, 1999), 3rd edition, p. 308.
• ^12.
  R. Eisberg e R. Resnick, Física Quântica – Átomos, Moléculas, Sólidos, Núcleos e Partículas (Editora Campus, Rio de Janeiro, 1979).
• ^13.
  N.L. Silva Junior e A.V. Andrade-Neto, Revista Brasileira de Ensino de Física 35, 3306 (2013).
• ^14.
  D. Drosdoff e A. Widom, Am. J. Phys. 73, 973 (2005).

• 1
  Por sua natureza, a velocidade do fóton é sempre c em qualquer meio. Todavia, em um meio material o fóton é continuamente absorvido e reemitido pelos átomos do material. Do atraso no deslocamento, gerado pelo tempo de absorção e a reemissão, resulta um valor de velocidade média para a propagação da luz em um meio transparente dada por v = c/n, que é necessariamente menor que o valor no vácuo.

Datas de Publicação

• Publicação nesta coleção
  08 Jan 2021
• Data do Fascículo
  2021

Histórico

• Recebido
  20 Ago 2020
• Revisado
  01 Dez 2020
• Aceito
  01 Dez 2020