Abstract
We prove the approximate controllability of the semilinear heat equation in R N, when the nonlinear term is globally Lipschitz and depends both on the state u and its spatial gradient <FONT FACE=Symbol>Ñ</FONT>u. The approximate controllability is viewed as the limit of a sequence of optimal control problems. In order to avoid the difficulties related to the lack of compactness of the Sobolev embeddings, we work with the similarity variables and use weighted Sobolev spaces.
approximate controllability; optimal control; unbounded domains; weighted Sobolev spaces
Approximate controllability for the semilinear heat equation in
N involving gradient termsSilvano Bezerra de Menezes* * Partially supported by the Alfa Project of the EU ''Modelisation et Ingenierie Mathématique'' during the preparation of this work at Universidad Complutense de Madrid.
Departamento de Matemática, Universidade Federal do Pará 66075-110 Belém, PA, Brazil E-mail: silvano@ufpa.br
ABSTRACT
We prove the approximate controllability of the semilinear heat equation in
N, when the nonlinear term is globally Lipschitz and depends both on the state u and its spatial gradient Ñu. The approximate controllability is viewed as the limit of a sequence of optimal control problems. In order to avoid the difficulties related to the lack of compactness of the Sobolev embeddings, we work with the similarity variables and use weighted Sobolev spaces.Mathematical subject classification: 93B05, 73C05, 35B37.
Key words: approximate controllability, optimal control, unbounded domains, weighted Sobolev spaces.
1 Introduction
Let W be a domain of
N with N Í 1. Given T > 0 and an open nonempty subset w of W we consider the following semilinear heat equation
In (1.1) 1w denotes the characteristic function of w. Roughly speaking, f is assumed to be mensurable in (x, t) and globally Lipschitz in the variables u and Ñu. In (1.1) u = u(x, t) is the state and h = h(x, t) is the control function which acts on the system through the subset w. The approximate controllability problem can be formulated as follows: Given a finite time horizon T > 0 and an arbitrary element u0Î L2(W), system (1.1) is said to be approximately controllable at time T in L2(W) if the reachable set
RNL(T) = {u(x, T) u is solution of (1.1) with h Î L2(Q)}
is dense in L2(W).
There are numerous works treating the approximate controllability in the linear parabolic framework, see [L2] and its bibliography, when W is a bounded set. The first results for nonlinear systems were obtained in [H]. More recently, several situations have been considered by Fabre, Puel and Zuazua [FPZ] for the particular case in which f is a globally Lipschitz function depending only on u., i.e., f = f(u). Their proof is divided in two parts:
a) approximate controllability of the linearized systems;
b) fixed point technique.
This technique cannot be applied when W is an unbounded set since the compacteness of Sobolev's embeddings is one of the main ingredients used in b). In L. de Teresa and E. Zuazua [TZ], they proved the approximate controllability of the semilinear heat equation in unbounded domains by an approximation method, for the case f = f(u), f being globally Lipschitz. The method in [TZ] consists in approximating the domain W by a sequence of bounded domains WR = W Ç BR, where BR denotes the ball centered in zero of radius R. It is then proved that, in the limit as R tends to infinity, the approximate controls in WR provide an approximate control in the unbounded domain W.
Later on, L. de Teresa [T] proved the approximate controllability when W =
N by an alternative method that consists in writing the heat equation in the similarity variables and using the weighted Sobolev spaces introduced in [EK] to guarantee the compacteness of the Sobolev embeddings. Then, essentially, the methods in [FPZ] apply.When W is a bounded set, L. Fernandez and E. Zuazua [FZ] gave a proof of the approximate controllability for the system (1.1), f being globally Lipschitz, inspired in the work by J.L. Lions [L2] in which, roughly speaking, the approximate controllability is viewed as the limit of a sequence of optimal control problems. More precisely, given u0Î L2 (W), u1Î H (W) with 0 < s < 1 and k > 0, let us consider the functional
(W) with 0 < s < 1 and k > 0, let us consider the functional
where uh denotes the solution of (1.1) with control h. The functional Jk is well defined for h Î L2(W × (0, T)). On the other hand, it is shown that, for each k > 0, there exists a minimizer hk of Jk in L2 (W × (0, T)). Let us denote by uk the solution of (1.1) associated to this minimizer. It is shown in [FZ] that
as k 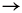 +¥, and therefore uk(T)
+¥, and therefore uk(T) 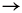 u1 in L2(W) as k
u1 in L2(W) as k 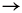 +¥. This fact, combined with the fact that H
+¥. This fact, combined with the fact that H (W) is dense in L2(W), guarantees the approximate controllability of system (1.1).
(W) is dense in L2(W), guarantees the approximate controllability of system (1.1).
This paper is devoted to analyze the approximate controllability of system (1.1) in case when W =
N. We adopt the approach in [FZ] but in the more general case W = N. However, in order to avoid the difficulties associated with the lack of compactness of the Sobolev embeddings, we work with similarity variables and the weighted Sobolev spaces as in [T]. We should point out we have essentially combined the techniques from both works [FZ] and [T]. A key point in the proof of our result is aresult of unique continuation by C. Fabre [Fa] in the context of linear heat equations involving gradient terms. The result in [Fa] allow us to conclude that
N. However, in order to avoid the difficulties associated with the lack of compactness of the Sobolev embeddings, we work with similarity variables and the weighted Sobolev spaces as in [T]. We should point out we have essentially combined the techniques from both works [FZ] and [T]. A key point in the proof of our result is aresult of unique continuation by C. Fabre [Fa] in the context of linear heat equations involving gradient terms. The result in [Fa] allow us to conclude that
provided a Î L¥ (Q) and b Î (L¥ (Q))N.
Thus, we consider the domain W to be
N, w an open nonempty subset of N and analyze the approximate controllability of the system:
N and analyze the approximate controllability of the system:
The main result of this paper is the following:
Theorem 1.1. Let us assume the following hypotheses:
where K0is a positive constant. Then, for any u0Î L2( N) and T > 0, the set of reachable states (at time T > 0) given by
N) and T > 0, the set of reachable states (at time T > 0) given by
RNL(T) = {uh,u º (x, T): uh,u º is the solution of (1.2) with
h Î L2 ( N x (0, T))}
N x (0, T))}
is dense in L2( N).
N).
Remark 1.1.
a) As we mentioned above, the method of proof applies in the case where W is a cone of
N (i.e. lW = W, "l > 0). Extending Theorem 1.1 to the case of general open unbounded sets W is an open problem. At this respect, the approximation method developed in [TZ] may be the most suitable tool.b) By an approximation argument, the assumption that f is C1 in the variables (u, Ñu) can be easily relaxed. It is sufficient f to be Lipschitz in those variables.
c) The assumption that f is globally Lipschitz in (u, Ñu) might seem to be artificial. But it is not. As it is shown in E. Fernández-Cara [F], there are nonlinearities growing at infinity in a slightly superlinear way and for which the approximate controllability fails.
The rest of the paper is organized as follows: in section 2, we introduce the similarity variables and use weighted Sobolev spaces. We prove basic results on existence, uniqueness and regularity of solutions. In section 3 we state some preliminary results concerning the solutions by transposition and we prove the approximate controllability of the linear equation. Section 4 is devoted to prove the main result. Finally, in section 5, we briefly comment the case of general conical domains.
2 Similarity variables and weighted Sobolev spaces
In this section we recall some basic facts about the similarity variables and weighted Sobolev spaces for the heat equation. We refer to [EK] and [K] for further developments and details. As we said above, to prove Theorem 1.1 we follow the approach in [FZ]. Thus, first we consider the problem of approximate controllability for the linearized system with potentials:
with a(x, t) Î L¥ ( N × (0, T)) and b(x, t) Î (L¥ (
N × (0, T)) and b(x, t) Î (L¥ ( N × (0, T)))N. The approximate controllability of (2.1) is then obtained as a singular limit of a sequence of optimal control problems. But, to do that, the lack of compactness of the Sobolev embedding in
N × (0, T)))N. The approximate controllability of (2.1) is then obtained as a singular limit of a sequence of optimal control problems. But, to do that, the lack of compactness of the Sobolev embedding in  N is an obstacle. To avoid it we work on the similarity variables of the heat equation and the weighted Sobolev spaces introduced in [EK] that we recall now.
N is an obstacle. To avoid it we work on the similarity variables of the heat equation and the weighted Sobolev spaces introduced in [EK] that we recall now.
We introduce the new space-time variables
Then, given u = u(x, t) solution of (2.1) we introduce v(y, s) = esN/2u(es/2y, es 1). It follows that u solves (2.1) if and only if v satisfies
where
The elliptic operator appearing in (2.3) may also be written as
where K = K(y) is the Gaussian weight K(y) = exp(|y|2/4). We introduce the weighted Lp-spaces:
For p = 2, L2(K) is a Hilbert space and the norm |·|L2(K) is induced by the inner product (f, g) =  f(y)g(y)K(y)dy. We then define the unbounded operator L on L2(K) by setting Lf = Df
f(y)g(y)K(y)dy. We then define the unbounded operator L on L2(K) by setting Lf = Df  as above, and D(L) = {f Î L2(K) : Lf Î L2(K)}. Integrating by parts it is easy to see that
as above, and D(L) = {f Î L2(K) : Lf Î L2(K)}. Integrating by parts it is easy to see that
Therefore it is natural to introduce the weighted H1-space:
endowed with the norm  . In a similar way, for any s Î
. In a similar way, for any s Î  and multi-index a we may introduce the space
and multi-index a we may introduce the space
Hs(K) {f Î L2 (K) : Daf Î L2 (K), "a, |a| < s}
The following properties were proved in [EK] and [K]:
is an isomorphism where (H1(K))* denotes the dual space of H1(K).
Since the operator L defined above has compact inverse in L2 (K), the equation
can be studied in the same manner as the heat equation in a bounded region W of
N. Let us recall some important and useful facts about the spaces appearing this paper. First, we introduce some notation. In fact, given two separable Hilbert spaces V and H such that V Ì H with continuous embedding, V being dense in H, let us consider the Hilbert space W(0, T, V, H) = {u Î L2(0, T, V) : ut Î L2(0, T, H)}, equipped with the norm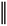
u
W(0,T,V,H) =
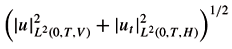
see, for instance [DL].
We have
We represent by (, ), |·|, ((, )) and  ·
· the inner product and norm, respectively, of L2(K) and H1(K). We observe that the operator L is defined by the triplet
the inner product and norm, respectively, of L2(K) and H1(K). We observe that the operator L is defined by the triplet
Therefore we have the following result about existence and uniqueness of the linear system (2.12). (See, for instance, [L1]).
Proposition 2.1. Given j Î L2 (0, S, L2(K)) and v0Î L2(K), there exists a unique solution v in the space W(0, S, H1(K), L2(K)) of problem (2.12). Moreover, if v0Î H1(K), then v Î W(0, S, H2(K), L2(K)).
3 Solutions by transposition and the linear case
In this section we give a precise definition of (2.12) in the sense of transposition and prove an existence and uniqueness result. The main question we are concerned here consists in finding a solution p of the parabolic problem:
when f Î (H1(K))*. Here (H1(K))* denotes the dual of H1(K). A function p Î L2(0, S, L2(K)) is called an solution of (3.1) obtained by transposition if
for any solution v of problem (2.12) with j Î L2(0, S, L2(K)) and v0(y) = 0 in  N. We represent by á , ñ the duality pairing between (H1(K))* and H1(K). We have
N. We represent by á , ñ the duality pairing between (H1(K))* and H1(K). We have
Proposition 3.1. If f Î (H1(K))* then there exists an unique solution p Î L2(0, S, L2(K)) Ç C([0, S], (H1(K))*) of problem (3.1).
Proof. Let us consider the linear form F : L2 (0, S, L2(K)) 
 defined by
defined by
where v is the solution of (2.12), with v0 = 0, corresponding to j.
Since v0 = 0, it is easy see that
Thus, F is a continuous linear form in L2(0, S, L2(K)). By Riesz's representation theorem, there exists a unique p Î L2(0, S, L2(K)) such that
The uniqueness is consequence of the Du Bois Raymond Lemma. Moreover,
Thus, by (3.2), (3.3) and (3.5), we have
Since f Î (H1(K))*, there exists (fm)mÎ with fm Î L2(K) for all m, such that
with fm Î L2(K) for all m, such that
Let (pm)mÎ be the sequence of solutions corresponding to fm for each m. Obviously, the function pn pm is the solution by transposition corresponding to fn fm.
be the sequence of solutions corresponding to fm for each m. Obviously, the function pn pm is the solution by transposition corresponding to fn fm.
From (3.6) and (3.7) we have that (pm)mÎ is a Cauchy sequence in L2(0, S, L2(K)) and
is a Cauchy sequence in L2(0, S, L2(K)) and
On the other hand,
Then, for each y Î L2 (0, S, H2(K)) we have
and this implies that ( )mÎ
)mÎ is a Cauchy sequence in L2(0, S, (H2(K))*).
is a Cauchy sequence in L2(0, S, (H2(K))*).
Therefore, we have
pm p strongly in W(0, S, L2(K), (H2(K))*)
p strongly in W(0, S, L2(K), (H2(K))*)
and this space is continuously embedded in C([0, S],(H1(K))*). We obtain pm  p strongly in C([0, S], (H1(K))*). In particular, p Î C([0, S], (H1(K))*).
p strongly in C([0, S], (H1(K))*). In particular, p Î C([0, S], (H1(K))*).
Through this work we set the notation q¢ = {(y, s), s Î (0, S), y Î w¢(s)}, where w¢(s) = es/2 and w is an open nonempty subset of  N.
N.
To prove the approximate controllability of system (2.12) we employ the theorem of unique continuation due to C. Fabre [Fa], Theorem 1.4 of [Fa]. We have
Proposition 3.2. Let w be an open and nonempty set of N, w¢(s) = es/2w and q¢ defined above. Assume that A(y, s) Î L¥(
N, w¢(s) = es/2w and q¢ defined above. Assume that A(y, s) Î L¥( N × (0, S)), B(y, s) Î (L¥(
N × (0, S)), B(y, s) Î (L¥( N × (0,S)))N. Let p Î L2 (0, S, H1(K)) be such that
N × (0,S)))N. Let p Î L2 (0, S, H1(K)) be such that
Then p º 0.
Proof. L, A and B do satisfy the conditions of Theorem 1.4 due Fabre [Fa] and the assumption of p implies that p Î  (0, S,
(0, S,  (
( N)). Consequently p º 0.
N)). Consequently p º 0.
Now, we have all the ingredients to prove our result:
Theorem 3.1 (Approximate controllability in H1(K)). Given bounded, measurable potentials A and B with S > 0, for every v0Î H1(K), the set of reachable states at time S > 0,  is the solution of (2.12) with j Î L2 (0, S, L2(K))} is dense in H1 (K).
is the solution of (2.12) with j Î L2 (0, S, L2(K))} is dense in H1 (K).
Proof. The proof follows the arguments in [FZ].
Because of the linearity of (2.12), we can assume without loss of generality that v0 = 0 and we denote the solution vj,0 by vj. Given a fixed element vd Î H1 (K) and k Î  , we introduce the following optimal control problem
, we introduce the following optimal control problem
For all k Î  the functional Jk is lower semicontinuous and strictly convex. Observe that the functional Jk is coercive in the Hilbert space of L2(0, S, L2(K)) of functions with support in q¢. Then, there exists a solution jk of (Pk) for each k Î
the functional Jk is lower semicontinuous and strictly convex. Observe that the functional Jk is coercive in the Hilbert space of L2(0, S, L2(K)) of functions with support in q¢. Then, there exists a solution jk of (Pk) for each k Î  . The derivative of Jk(j) is given by
. The derivative of Jk(j) is given by
for all x Î L2(0, S, L2(K)). If we evaluate  · x in the solution jk of (Pk) we must have
· x in the solution jk of (Pk) we must have
for all x Î L2(0, S, L2(K)), with vk(S) = vjk(S).
Taking into account that Jk (jk) < Jk(0) =  for every k Î
for every k Î  , we deduce that {vk(S)-vd}kÎ
, we deduce that {vk(S)-vd}kÎ is a bounded sequence in H1(K) and
is a bounded sequence in H1(K) and  is bounded in L2(0, S, L2 (K)). Then we can extract a subsequence {vk(S)-vd}k Î
is bounded in L2(0, S, L2 (K)). Then we can extract a subsequence {vk(S)-vd}k Î such that
such that
From (3.12) we obtain:
By transposition we define the adjoint state p as the unique solution (cf. section 3) of the problem:
We obtain
for all z Î W(0, S, H2(K), L2(K)), such that z(0) = 0.
The solution p of (3.15) defined by (3.16) has the regularity:
cf. Proposition 3.1.
Let us consider z the solution of (2.12) when j = x; this solution we denote by vx. From relation (3.16) it follows that
It follows that p(x, t) = 0, a.e. (y, s) Î w¢ × (0, S) and by Proposition 3.2 we have p(x, t) = 0, a.e. (y, s) Î  N × (0, S). Since p Î
N × (0, S). Since p Î  ([0, S], (H1(K))*) and p(S) = Ly with y Î H1(K) we have y = 0. From (3.13) we have
([0, S], (H1(K))*) and p(S) = Ly with y Î H1(K) we have y = 0. From (3.13) we have
vk(S)  vd weakly in H1(K).
vd weakly in H1(K).
The strong convergence follows from (3.12) with x = jk. Indeed, letting k  ¥ in
¥ in
we obtain that vk(S)  vd strongly in H1(K).
vd strongly in H1(K).
Corollary 3.1. For every v0Î H1(K) and m Î [0,1), the set  (S) is dense in Hm(K).
(S) is dense in Hm(K).
Proof. This is a direct consequence of Theorem 3.1 and the density of H1(K) in Hm(K).
Corollary 3.2. For every v0Î L2(K), the set  (S) is dense in L2(K).
(S) is dense in L2(K).
Proof. Let us consider v1Î L2 (K) and e > 0. Since H1 (K) Ì L2(K) with dense inclusion, there exists a sequence {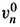 } Ì H1 (K) such that
} Ì H1 (K) such that  strongly in L2(K).
strongly in L2(K).
From Corollary 3.1, we know the existence of controls jn such that the solution  of (2.12) with j = jn satisfies
of (2.12) with j = jn satisfies
Let Ñ > 0 be such that  where c > 0 is a constant that will appear bellow. Consider vj, v0 the solution of (2.12) corresponding to v0 and j = jÑ. Let z =
where c > 0 is a constant that will appear bellow. Consider vj, v0 the solution of (2.12) corresponding to v0 and j = jÑ. Let z =  . Then z satisfies
. Then z satisfies
We multiply (3.17) by zK(y) and integer over  N. Then, there exists a constant c > 0 such that |z(S)|L2(K)<
N. Then, there exists a constant c > 0 such that |z(S)|L2(K)<  and, therefore,
and, therefore,
We conclude with the
Theorem 3.2. Given u0Î L2( N) the set of reachable states at time T > 0, RL(T) = {uh,u0(T) : uh, u0 is the solution of (2.1) with h Î L2(
N) the set of reachable states at time T > 0, RL(T) = {uh,u0(T) : uh, u0 is the solution of (2.1) with h Î L2( N× (0, T))} is dense in L2(
N× (0, T))} is dense in L2( N ).
N ).
Proof. Let us consider u1Î L2( N) and e > 0. We divide the proof into three steps.
N) and e > 0. We divide the proof into three steps.
Step 1. The case u0 = 0, u1Î L2(K).
Let us consider v1(y) = (T + 1)N/2u1 ((T + 1) y) Î L2(K). From Corollary 3.2 we know the existence of j Î L2(0, S, L2(K)) such that |v(S) - v1|L2(K)< e, with S = log(T + 1). Then
y) Î L2(K). From Corollary 3.2 we know the existence of j Î L2(0, S, L2(K)) such that |v(S) - v1|L2(K)< e, with S = log(T + 1). Then
is the solution of (2.1) with
and
Step 2. The case u0 = 0, u1Î L2( N).
N).
Since L2(K) Ì L2( N) with dense inclusion, there exists a sequence {
N) with dense inclusion, there exists a sequence { } and Ñ > 0 such that |
} and Ñ > 0 such that | - u1|L2(
- u1|L2(
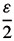 for every n > Ñ.
for every n > Ñ.
From the first step, we know the existence of controls hn such that un the solution of (2.1) with h = hn satisfies
Then, the solution u of (2.1) with h = hÑ satisfies
Step 3. The general case, i.e. u0, u1Î L2( N) arbitrary.
N) arbitrary.
We write u = z + Y where z is the solution of
Then z(T) Î L2( N). We construct h = h(u1 - z(T)) such that the solution of
N). We construct h = h(u1 - z(T)) such that the solution of
satisfies
Therefore in (2.1) it is enough to chose h = h(u1 - z(T)) since the unique solution is u = z + Y and in view of (3.20) we conclude the proof.
4 The non linear case
We will now study the same problem for the semilinear heat equation (1.2). As in the linear case, a change of variables v(y, s) =  transforms the system (1.2) in
transforms the system (1.2) in
with g(y, s, v, Ñ v) = es(N+2)/2f(es/2y, es - 1, e-s N/2v, e-s(N+2)/2Ñ v) and j(y, s) = es(N+2)/2h(es/2y, e2 - 1).
We must remark the function g = g(y, s, q, h) possesses the same properties as f. In particular, g is globally Lipschitz in the variables (q, h).
Observe that by (1.4) and because L2(K) is dense in L2( N) we can consider f(x, t, 0, 0) in L2 (0, T, L2(K)). This guarantees that g(y, s, 0, 0) Î L2(0, S, L2(K)). Thus, we suppose that f also satisfies
N) we can consider f(x, t, 0, 0) in L2 (0, T, L2(K)). This guarantees that g(y, s, 0, 0) Î L2(0, S, L2(K)). Thus, we suppose that f also satisfies
besides (1.3) and (1.5).
From the embedding (I1)-(I4) and g globally Lipschitz, it follows the following result on existence and uniueness for system (4.1).
Proposition 4.1. Suppose f satisfying the conditions (1.3), (1.5) and (4.2) above. Then, given j Î L2 (0, S, L2(K)) and v0Î L2(K), there exists a unique solution v in the space W(0, S, H1(K), (H1(K))*) of problem (4.1). Moreover, if v0Î H1(K), hence v Î W(0, S, H2(K), L2(K)).
Proof. The proof is the same given for Theorem 1 in [FZ].
We observe that, in view of Proposition 4.1 and change of variables, if u0 = v0Î L2(K) and f Î L2(0, T, L2(K)) then there exists a unique solution u Î W(0, T, H1(K), (H1(K))*) of problem (1.2).
As usual, it is possible to derive the continuous dependence of the solution with respect to the initial data:
Proposition 4.2 (Continuity with respect to the data). Suppose g satisfying the conditions above.
a) Let us suppose
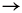 v0 in L2(K) and jm
v0 in L2(K) and jm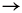 j in L2(0, S, L2(K)). Then, in W(0, S, H1(K), (H1(K))*).
j in L2(0, S, L2(K)). Then, in W(0, S, H1(K), (H1(K))*).
b) Let us suppose
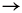 v0 in L2(K) and jm
v0 in L2(K) and jm j in H1(0, S, L2(K)). Then, in W(0, S, H2(K), (L2(K))*).
j in H1(0, S, L2(K)). Then, in W(0, S, H2(K), (L2(K))*).
To show the approximate controllability property of the semilinear heat equation, we are going to introduce a family of optimal control problems. A previous step for establishing the optimality conditions corresponding to their solutions in the study of the differentiability of the functional involved.
Proposition 4.3 (Differentiability with respect to the data). Suppose that g satisfies the conditions above. Given v0Î H1 (K), the functional F : L2(0, S, L2(K))  H1(K) defined by F(j) = vj, v0 (S) is differentiable. Moreover, DF (j)y = zy (S), where zy is the unique solution in W(0, S, H2(K), L2(K)) of the following linearized problem
H1(K) defined by F(j) = vj, v0 (S) is differentiable. Moreover, DF (j)y = zy (S), where zy is the unique solution in W(0, S, H2(K), L2(K)) of the following linearized problem
Proof. The functional F is well defined by Proposition 4.1 and the embedding (2.16). Given j, y Î L2(0, S, L2(K)) and l Î (0,1), let us denote vl = vj+ly,v0, v = vj,v0 and zl =  (vl - v). To show that F is Gâteaux differentiable we have to prove that
(vl - v). To show that F is Gâteaux differentiable we have to prove that
It is clear that for each l we have
where zl,s denotes  .
.
By the Mean Value Theorem, we have
where wl = v + x(vl - v), 0 < x < 1 depends on y, s and l. Applying (4.5) to zlK(y), integrating by parts, using the fact that g is globally Lipschitz in the variable (v, Ñv) and Young's inequality, we deduce the existence of a constant c1 > 0 such that
Using Gronwall inequality, we have
|zl(s)|L2(K)< ec1S|y|L2(0,S,L2(K)), " s Î [0, S], " l Î (0, 1).
Thus, the sequence {zl} is bounded in  ([0, S], L2(K)) and by (4.7), {zl} is bounded in L2(0, S, H1(K)). In fact, |zl|L2(0,S,H1(K))< ec1S |y|L2(0,S,L2(K)), " l Î (0,1). Taking into account this estimate together with the equation (4.5), (4.6) and hypothesis on g, we conclude that there exists a positive constant c2 (independent on l and y) such that
([0, S], L2(K)) and by (4.7), {zl} is bounded in L2(0, S, H1(K)). In fact, |zl|L2(0,S,H1(K))< ec1S |y|L2(0,S,L2(K)), " l Î (0,1). Taking into account this estimate together with the equation (4.5), (4.6) and hypothesis on g, we conclude that there exists a positive constant c2 (independent on l and y) such that
|zl|W(0,S,H1(K),H1(K))*)< c2|y|L2(0,S,L2(K)), " l Î (0, 1).
In view of the expression of gl and using classical estimates, we deduce the existence of a positive constant c3 (still independent of l and y) such that
Thus, by extracting subsequences,
Combining this convergence with the compact imbedding (2.15) and Proposition (4.2b), we deduce that
It is then easy to see, by the well-posedness properties of (4.5), that  = zy and that the convergence in (4.9) holds in the strong topology. Using the embedding (2.16), we obtain (4.4).
= zy and that the convergence in (4.9) holds in the strong topology. Using the embedding (2.16), we obtain (4.4).
We have the following result on approximate controllability for the system (4.1):
Theorem 4.4. For each v0Î H1(K) the set of admissible states at S > 0,
 (S) = {vj,v0 (S): vj,v0is solution of (4.1) with j Î L2(0, S, L2(K))}
(S) = {vj,v0 (S): vj,v0is solution of (4.1) with j Î L2(0, S, L2(K))}
is dense in Hm(K), for each 0 < m < 1.
Proof. We know that H1(K) is dense in Hm(K) for 0 < m < 1. Then, it is sufficient to prove that  (S) is dense in H1(K) with the norm of Hm(K) for 0 < m < 1.
(S) is dense in H1(K) with the norm of Hm(K) for 0 < m < 1.
In fact, let us take vd Î H1(K), 0 < m < 1 and consider the functional defined in L2(0, S, L2(K)) by:
This functional is lower semicontinuous and coercive in the Hilbert space of L2(0, S, L2(K)) of functions with support in q¢. It follows that the minimization problem (Pk) given by:
has at least one solution jk.
Thanks to Proposition 4.3, the first order optimality condition associated with the minimization problem (Pk) at this minimum gives
for all y Î L2 (0, S, L2(K)), where vk = vjk,v0 and  is the unique function in W(0, S, H2(K), L2(K)) solution of the problem
is the unique function in W(0, S, H2(K), L2(K)) solution of the problem
By the minimum condition we have Jk(jk) < Jk(0) for every k Î  . It follows that {vk(S) - vd}kÎ
. It follows that {vk(S) - vd}kÎ is a bounded sequence in Hm(K) and
is a bounded sequence in Hm(K) and  is a bounded sequence in L2(0, S, L2(K)). Thus, by extracting subsequences,
is a bounded sequence in L2(0, S, L2(K)). Thus, by extracting subsequences,
Moreover, there exist c Î L¥( N × (0, S)) and d Î (L¥(
N × (0, S)) and d Î (L¥( N × (0, S)))N such that
N × (0, S)))N such that
Let zy be the unique solution of the problem
Suppose that
By (4.10), (4.12) and (4.15) we obtain:
and when k  ¥, we have
¥, we have
By Theorem 3.1 the set {zy(S)} is dense in H1(K) and, therefore, in Hm(K), when y varies in L2(0, S; L2(K)). Consequently, (4.16) implies that q º 0. Therefore, according to (4.12), vk(S)  vd weakly in Hm(K). Since the embedding Hm(K) Ì Hm¢(K) is compact for m¢ < m, we conclude the strong convergence in Hm¢(K), for any m¢ < m. Taking into account that this holds for all m < 1, we conclude the density in Hm(K), as stated in Theorem 4.4.
vd weakly in Hm(K). Since the embedding Hm(K) Ì Hm¢(K) is compact for m¢ < m, we conclude the strong convergence in Hm¢(K), for any m¢ < m. Taking into account that this holds for all m < 1, we conclude the density in Hm(K), as stated in Theorem 4.4.
To complete the proof we need to proof the convergence (4.15). In fact, multiplying (4.11) by K(y) , integrating in
, integrating in  N and observing that
N and observing that
we have
Multiplying (4.11) by K(y) ( )¢ and integrating in
)¢ and integrating in  N, we obtain:
N, we obtain:
From (4.18) and (4.19) it follows that { }kÎ
}kÎ is bounded in W(0, S, H2(K), L2(K)). Since W(0, S, H2(K), L2(K)) is compactly embedded in L2(0, S, H1(K)), there exists subsequences such that
is bounded in W(0, S, H2(K), L2(K)). Since W(0, S, H2(K), L2(K)) is compactly embedded in L2(0, S, H1(K)), there exists subsequences such that
From (4.15) and (4.20) we can pass to the limit in (4.11) obtaining that c is the solution of (4.14) and by uniqueness c = zy. On the other hand, from (4.20) and the continuous embedding I4) we have:
and k tends to +¥. The embedding of H1(K) into Hm(K) into Hm(K) being compact, for m < 1. This proves (4.15).
Corollary 4.1. Given v0Î L2 (K), the set  (S) is dense in L2(K).
(S) is dense in L2(K).
Proof. As in the proof of Corollary 3.2, let us consider v1Î L2(K) and e > 0. Then, there exists a sequence {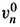 }nÎ
}nÎ Ì H1(K) such that
Ì H1(K) such that 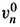
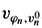 , the solution of (4.1) corresponding to
, the solution of (4.1) corresponding to 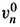 and jn, satisfies
and jn, satisfies
Let Ñ > 0 be such that
where c > 0 is a constant that will be timely introduced.
Consider vj,v0 the solution of (4.1) corresponding to v0 and j = jÑ. Let  . Then, z satisfies
. Then, z satisfies
We multiply (4.21) by zK(y) and integer over  N. Since g satisfies (4.17), we obtain
N. Since g satisfies (4.17), we obtain
We conclude with the proof of Theorem 1.1.
Proof of Theorem 1.1. Let us consider a > 0 and u1Î L2( N). As in the proof of Theorem 3.2 we divide into several steps.
N). As in the proof of Theorem 3.2 we divide into several steps.
First step. The case u0, u1 in L2(K).
We make the change of variables v1(y) = (1 + T)N/2u1((1 + T)1/2y) and S = log(1 + T). Then v1Î L2(K) and by Corollary 4.1, there exists j Î L2(0, S, L2(K)) such that the solution v of (4.1) corresponding to v0 and j, satisfies
We define
Then u is solution of (1.2) with
and |u(T)  < a2 (cf. Theorem 3.2, Step 1).
< a2 (cf. Theorem 3.2, Step 1).
Second step. The case u Î L2(K), u1Î L2( N).
N).
Since L2(K) Ì L2( N) with dense inclusion, there exists a sequence {
N) with dense inclusion, there exists a sequence { }nÎ
}nÎ Ì L2(K) such that
Ì L2(K) such that 
 N). From the First Step, we know that existence of controls hn such that un the solution of (1.2) satisfies
N). From the First Step, we know that existence of controls hn such that un the solution of (1.2) satisfies 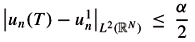 . Let Ñ > 0 such that for every n > Ñ,
. Let Ñ > 0 such that for every n > Ñ, 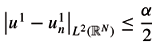 .
.
Then, u the solution of (1.2) with h = hÑ satisfies |u(T) - u1|L2(
)< a.Third step. The case u0Î L2( N).
N).
Then there exists a sequence {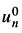 } with
} with 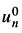 Î L2(K) such that
Î L2(K) such that 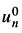
 N). Given u1Î L2(
N). Given u1Î L2( N) and a > 0, as we saw previously, there exists a sequence of controls hn such that un, the solution of (1.2) corresponding to
N) and a > 0, as we saw previously, there exists a sequence of controls hn such that un, the solution of (1.2) corresponding to 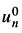 and hn, satisfies
and hn, satisfies
Let Ñ > 0 be such that
K0 the constant given in (1.5).
Consider u the solution of (1.2) corresponding to u0 and h = hÑ. Let z = u-uÑ. Then, z satisfies
We multiply (4.22) by z and integer over  N. Since f satisfies (1.5), we obtain
N. Since f satisfies (1.5), we obtain
Then,  and therefore
and therefore
5 Conical domains
Consider a cone-like domain W satisfying:
All the results of these paper hold for the semilinear heat equation (1.1) when W is a cone-like domain. In fact, consider a domain W satisfying (5.1). Then if one consider the evolution equation
we can study the controllability of the equation (5.2) in the same way as the case of the whole space
N. Observe that defining v, g and j like in this section we obtain that v satisfies
The operator Lf = - div(K Ñ f), K(y) = exp (|y|2/4), is self-adjoint in L2(K, W) with compact inverse and
div(K Ñ f), K(y) = exp (|y|2/4), is self-adjoint in L2(K, W) with compact inverse and
where
Indeed, the methods of the previous sections apply. First of all, the approximate controllability of the linearized equation can be obtained as a consequence of the unique continuation result in [Fa]. Then, the approximate controllability for the semilinear system can be proved by viewing this property as the limit of optimality conditions of penalized optimal control problems.
6 Acknowledgement
My appreciation to E. Zuazua who drew my attention to this problem, for reading the manuscript and for his valuable suggestions.
Received: 2/II/02.
#543/02.
- [CMZ] V. Cabanillas, S. Menezes and E. Zuazua, Null controllability in unbounded domains for the semilinear heat equation with nonlinearities involving gradient terms, J. Optm. Theory Appls., 110, 2, (2001), 246-264.
- [DL] R. Dautray and J.L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology, Springer-Verlag, (1992).
- [EK] M. Escobedo and O. Kavian, Variational Problems Related to Self-Similar Solutions of Heat Equation, Nonl. Anal. TMA, 11, 10, (1997), 1103-1133.
- [EZ] M. Escobedo and E. Zuazua, Large Time Behaviour for Convection-diffusion Equations in Rn J. Funct. Anal., 100 (1991), 119-161.
- [F] E. Fernández-Cara, Null controllability of the semilinear heat equation, ESAIM: COCV 2 (1997), 87-107.
- [Fa] C. Fabre, Uniqueness results for Stokes equations and their consequences in linear and nonlinear control problems, ESAIM: COOCCV, 1 (1996), 267-302.
- [FI] A. Fursikov, O. Yu, Imanuvilov, Controllability of evolution equations, Lecture Notes, Vol. 34 (1996), Seoul National University, Korea.
- [FPZ] C. Fabre, J.P. Puel and E. Zuazua, Approximate controllability of the semilinear heat equation, Proc. Royal Soc. Edinburgh, 125A (1995), 31-61.
- [FZ] L.A. Fernández and E. Zuazua, Approximate controllability for the semilinear heat equation involving gradient terms, J. Opt. Theo. and Appl., 101 (1999), 307-328.
- [FCZ1] E. Fernández-Cara and E. Zuazua, The cost of approximate controllability for heat equation: the linear case, Adv. Diff. Equations, 5, 4-6, (2000), 465-514.
- [FCZ2] E. Fernández-Cara and E. Zuazua, Controllability of weakly blowing-up semilinear heat equations, Ann. Inst. H. Poincaré, Anal. non lin., 17, 5, (2000), 583-616.
- [H] J. Henry, Contrôle d'un réacteur enzymatique ŕ l'aide de modčles ŕ paramčtres distribués. Quelques problčmes de contrôlabilité de systčmes paraboliques Ph.D. thesis, Université Paris VI, (1978).
- [IY] O. Yu, Imanuvilov and M. Yamamoto, On Carleman inequalities for parabolic equations in Sobolev spaces of negative order and exact controllability for semilinear parabolic equations, Preprint no. 98-46, University of Tokyo, Graduate School of Mathematics, Japan, 1998.
- [K] O. Kavian, Remarks on the large time behaviour of a nonlinear diffusion equation, Ann. Inst. Henri Poincaré, vol. 4, No. 5, (1987), 423-452.
- [LR] G. Lebeau and L. Robbiano, Contrôle exact de l'équation de la chaleur, Comm. P.D.E., 20 (1995), 335-356.
- [L1] J.L. Lions, Équations Differentielles Operationnelles, Springer-Verlag, (1961).
- [L2] J.L. Lions, Remarques sur la contrôlabilité approchée In Jornadas Hispano-Francesas sobre Control de Sistemas Distribuidos, pages 77-87, University of Málaga (Spain), 1991.
- [R] D.L. Russell, A unified boundary controllability theory for hyperbolic and parabolic partial differential equations, Studies in Appl. Math., 52 (1973), 189-221.
- [T] L. Teresa, Approximate controllability of a semilinear heat equation in RN, SIAM J. Cont. Optim., 36, 6, (1998), 2128-2147.
- [TZ] L. Teresa and E. Zuazua, Approximate controllability of the semilinear heat equation in unbounded domains, Nonl. Anal. T.M.A., 37, 8, (1999), 1059-1090.
Publication Dates
-
Publication in this collection
19 July 2004 -
Date of issue
2003
History
-
Received
02 Feb 2002



































































































