Abstract
This paper considers a pair of transmission problems for the system of piezoelectricity having piecewise constant coefficients. Under suitable monotonicity conditions on the coefficients and certain geometric conditions on the domain and the interfaces where the coefficients have a jump discontinuity, results on simultaneous boundary observation and simultaneous exact control are established.
Piezoelectricity; transmission problem; simultaneous exact controllability
Simultaneous exact control of piezoelectric systems in multilayered media
Boris V. KapitonovI, * * Visiting Researcher at the National Laboratory of Scientific Computation (LNCC/MCT). ; Marco Antonio RauppII
ISobolev Institute of Mathematics, Siberian Branch of Russian Academy of Sciences
IILaboratory of Scientific Computation, LNCC/MC, 25651-070 Quitandinha, Petrópolis, RJ, Brasil
E-mail: borisvk@lncc.br
ABSTRACT
This paper considers a pair of transmission problems for the system of piezoelectricity having piecewise constant coefficients. Under suitable monotonicity conditions on the coefficients and certain geometric conditions on the domain and the interfaces where the coefficients have a jump discontinuity, results on simultaneous boundary observation and simultaneous exact control are established.
Mathematical subject classification: 35L50; 35Q60; 35B40.
Key words: Piezoelectricity; transmission problem; simultaneous exact controllability.
1 Introduction
Throughout this paper W will be a bounded domain in
3 with sufficiently smooth boundary . For k = 1,2,...,n, let
. For k = 1,2,...,n, let 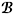 k be open, bounded and connected subsets of W with smooth boundary
k be open, bounded and connected subsets of W with smooth boundary  k, and such that
k, and such that 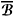 k Ì
k Ì 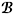 k+1. We set
k+1. We set
Assume that W is occupied by a linear multilayered piezoelectric body whose motion is governed by the following system ([4], [6])
where r is the mass density, u is the displacement vector,  u is the symmetric part of Ñu, T is the stress tensor, H is the magnetic field, E is the electric field,
u is the symmetric part of Ñu, T is the stress tensor, H is the magnetic field, E is the electric field,  is the electric displacement vector, m is the magnetic permeability, c, e, b are the elastic, piezoelectric and electric permittivity tensors respectively whose Cartesian components satisfy the following properties:
is the electric displacement vector, m is the magnetic permeability, c, e, b are the elastic, piezoelectric and electric permittivity tensors respectively whose Cartesian components satisfy the following properties:
for any real vector x = (x1, x2, x3) Î  3,
3,
for any real symmetric matrices {eij} of order 3.
We introduce the following matrices of order 3
where
It follows from the symmetry of cijkl that
Using these notations, we write the system (1.1) in the matrix form
We note that
where
It is assumed that
for any real vector hi Î  3. Here (·,·) denotes the inner product in
3. Here (·,·) denotes the inner product in  3. We remark that this assumption holds for an isotropic medium (cijkh =
3. We remark that this assumption holds for an isotropic medium (cijkh =  dijdkh +
dijdkh +  dikdjh +
dikdjh +  dihdjk) with a constant C0 =
dihdjk) with a constant C0 =  :
:
It is assumed that cijkh(x), bij(x), m(x) are piecewise constant functions which lose the continuity on  1,
1, 2,...,
2,..., n, r and ekhi are constants, r > 0.
n, r and ekhi are constants, r > 0.
We consider the following transmission problems
and
where [·,·] is the vector product, n = n(x) = (n1,n2,n3) (for x Î  m, x Î
m, x Î  ) is the unit normal vector pointing into the exterior of
) is the unit normal vector pointing into the exterior of 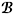 m or W;
m or W;  , u(m), v(m), E(m), F(m), H(m), Y(m) are the restrictions of the corresponding matrices and vector-functions on Wm. In (1.5) b = b(x) is a continuously differentiable positive function on
, u(m), v(m), E(m), F(m), H(m), Y(m) are the restrictions of the corresponding matrices and vector-functions on Wm. In (1.5) b = b(x) is a continuously differentiable positive function on  .
.
The problem of exact boundary control for the system (1.2)-(1.5) ((1.6)-(1.9)) is formulated as follows:
Given the initial distribution f = {f1,f2,f3,f4} (j = {j1, j2,j3,j4}), time T > 0, and a desired terminal state g = { g1, g2, g3, g4} (y = {y1, y2, y3, y4}) with f, g(j,y) in appropriate function spaces, find a vector-valued functions Q(x,t), G(x,t) ( (x,t),
(x,t), 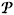 (x,t)) in a suitable function spaces such that the solution of (1.2)-(1.5) ((1.6)-(1.9)) satisfies the conditions
(x,t)) in a suitable function spaces such that the solution of (1.2)-(1.5) ((1.6)-(1.9)) satisfies the conditions
Our purpose is to obtain simultaneous exact boundary control of these problems, { (x,t),
(x,t),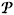 (x,t)} serving as a control in problem (1.6)-(1.9), while the vector-valued functions
(x,t)} serving as a control in problem (1.6)-(1.9), while the vector-valued functions
is a control in (1.2)-(1.5).
Spatial energy estimates for a semi-infinite piezoelectric beam have been studied by A. Borrelli and M.C. Patria [2].
Boundary controllability for some partial case of the system (1.1) with another boundary and interface conditions was investigated in [14].
For Ai º 0, the piezoelectric system (1.2) decouples into a pair of hyperbolic systems: the Maxwell system and the hyperbolic system of second order.
The exact controllability problem for the Maxwell system has been studied by D. Russell [27] for a circular cylindrical region, by K. Kime [16] for a spherical region, and by J. Lagnese [20] for a general region. Stabilization for the Maxwell system with the Silver-Müller absorbing boundary conditions and exact controllability for corresponding initial boundary value problem have been studied by V. Komornik [17], P. Martinez [24] and N. Weck [28]. The uniform exponential decay of solutions of Maxwell's equations with boundary dissipation and exact boundary controllability was proved in [7], [8].
Stabilization and exact boundary controllability for the system of elasticity have been studied by J. Lagnese [18], [19], F. Alabau and V. Komornik [1] and M. Horn [5] among others. In [7], [9] boundary observation, stabilization and exact controllability were studied for a class of hyperbolic systems which includes the system of elasticity.
Boundary controllability in transmission problems for a class of second order hyperbolic systems has been studied by J. Lagnese [19]. Uniform stabilization and exact control for the Maxwell system in multilayered media were investigated in [8]. The question of boundary controllability in transmission problems for the wave equation has been considered by J.-L. Lions [23], and S. Nicaise [25], [26].
The main novelty of this note is that we study the simultaneous exact control. Simultaneous exact control for the wave equation has been established by D. Russell [27] for a circular cylindrical region and by J.-L. Lions [22], F. Khodja and A. Bader [15].
In [9]-[13] simultaneous controllability were studied for a class of hyperbolic systems of second order, for a pair of Maxwell's equations and for a class of evolution systems which includes the Schrödinger equation.
This article is organized as follows: simultaneous boundary observation for the problems (1.2)-(1.5) and (1.6)-(1.9) with zero boundary conditions (Q º G º  º
º 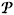 º 0) is established in Section 2. In Section 3 the simultaneous exact controllability is studied by means of the Hilbert Uniqueness Method, introduced by J.-L. Lions [21], [22].
º 0) is established in Section 2. In Section 3 the simultaneous exact controllability is studied by means of the Hilbert Uniqueness Method, introduced by J.-L. Lions [21], [22].
2 Boundary observability
Throughout this paper Hk(W) and Hq( ) denote the usual Sobolev spaces.
) denote the usual Sobolev spaces.
We denote by
0 the Hilbert space of pairs u = {u1(x),u2(x)} of three-component vector-valued functions
with the inner product
From the results of [3] it follows that the expressions [n, u1], [n, u2], (n = n(x), x Î  , x Î
, x Î  m,m = 1,2,...,n) are well defined on
m,m = 1,2,...,n) are well defined on  ,
,  m and belong to
m and belong to  .
.
This enables us to introduce in
0 the closed subspaces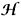 1,
1, 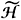 1:
1:
the space
1 is defined just as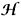 1 with the only difference that [n,u2] vanishes on
1 with the only difference that [n,u2] vanishes on  .
.
We denote by 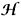 the real Hilbert space of quadruples w = { w1,w2, w3, w4} of three-component vector-valued functions wi(x) such that
the real Hilbert space of quadruples w = { w1,w2, w3, w4} of three-component vector-valued functions wi(x) such that
where  is the restriction of wi on Wm. The inner product in
is the restriction of wi on Wm. The inner product in 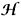 is given by
is given by
The space 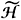 is defined just as
is defined just as 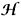 with the only difference that the first vector-valued function w1 vanishes on
with the only difference that the first vector-valued function w1 vanishes on  .
.
In 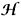 and
and 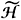 we define unbounded operators
we define unbounded operators  and
and  :
:
 (
( ) consists of the elements u = { u1, u2, u3, u4} Î
) consists of the elements u = { u1, u2, u3, u4} Î 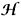 such that
such that
for u = { u1, u2, u3, u4} Î  (
( ).
).
The operator  is defined just as
is defined just as  with the only difference that elements
with the only difference that elements
satisfy another boundary conditions
The skew-selfadjointness of  and
and  can be verified in the standard way.
can be verified in the standard way.
Let  (t) and
(t) and  (t) be the strongly continuous groups of unitary operators generated by
(t) be the strongly continuous groups of unitary operators generated by  and
and  .
.
We set
Denote by M1 and  1 the orthogonal complements of M and
1 the orthogonal complements of M and  in
in 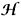 and
and 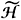 respectively.
respectively.
Let us consider the problem (1.2)-(1.5) with homogeneous boundary conditions (Q º G º 0). The kernel M of  * is nonempty, since it contains the quadruples w = {w1,0,Ñg1, Ñg2}, where g1Î H2(W), g2Î H2 (W)Ç
* is nonempty, since it contains the quadruples w = {w1,0,Ñg1, Ñg2}, where g1Î H2(W), g2Î H2 (W)Ç (W), w1 is a solution of the following problem
(W), w1 is a solution of the following problem
It is obvious that  (t) takes M1 Ç
(t) takes M1 Ç  (
( ) into itself. Indeed, if w Î M and v Î M2 Ç
) into itself. Indeed, if w Î M and v Î M2 Ç  (
( ), then
), then
We remark that element v = {v1,v2,v3,v4} Î M1 Ç  (
( ) possess the following property:
) possess the following property:
in the sense of distributions.
Indeed, element w = {w1, 0, Ñg1, 0} where g1Î H2(W), supp g1Ì Wm, w1 is a solution of the problem (2.1), belongs to M. Let v Î M1 Ç  (
( ). Then
). Then
for an arbitrary g1Î H2(W), supp g1Ì Wm, which implies
in the sense of distributions.
It can be shown in a similar way (element {0,0,0,Ñg2} belongs to M for an arbitrary g2Î H2(W), supp g2Ì Wm) that div  = 0 in the sense of distributions.
= 0 in the sense of distributions.
Let us show that elements v = {v1,v2,v3,v4} Î M1 Ç  (
( ) satisfy the boundary condition
) satisfy the boundary condition
We note that element w = {0,0,0,Ñg2} belongs to the kernel of  * for an arbitrary g2Î H2(W), g2 = 0 in
* for an arbitrary g2Î H2(W), g2 = 0 in  0È
0È  1È ... È
1È ... È  n1.
n1.
Thus, for v = {v1,v2,v3,v4} Î M1 Ç  (
( ) we have
) we have
which implies (2.3).
Our next goal is to show that elements v = {v1,v2,v3,v4} Î M1 Ç  (
( ) satisfy the following interface conditions
) satisfy the following interface conditions
Since w = {0,0,0,Ñg2} belongs to the kernel of  * for an arbitrary g2Î H2(W) Ç
* for an arbitrary g2Î H2(W) Ç  (W), it follows that
(W), it follows that
Now we choose g2 such that g2 = 0 on  1,...,
1,..., m1,
m1,  m+1,...,
m+1,..., n. Then
n. Then
and we have
Moreover, element w = {w1,0,Ñg1,0} belongs to the kernel of  * for an arbitrary g1Î
* for an arbitrary g1Î  (W) (w1 is a solution of (2.1)). We have
(W) (w1 is a solution of (2.1)). We have
We choose g1 such that g1 = 0 on  1,...,
1,..., m1,
m1, m+1,...,
m+1,...,  n. This gives us that
n. This gives us that
Let us consider now the problem (1.6)-(1.9) with homogeneous boundary conditions ( º
º 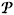 º 0). We remark that the kernel
º 0). We remark that the kernel  of
of  * contains the quadruples w = {w1, 0, Ñg1,Ñg2}, where g1Î H2(W), g2Î H2(W) Ç
* contains the quadruples w = {w1, 0, Ñg1,Ñg2}, where g1Î H2(W), g2Î H2(W) Ç  (W), w1 is a solution of (2.1) with the only difference that the functions w1 satisfy the boundary condition:
(W), w1 is a solution of (2.1) with the only difference that the functions w1 satisfy the boundary condition:
It can be shown in the same way that elements v = { v1, v2, v3, v4} Î  1Ç
1Ç  (
( ) satisfy (2.2), (2.4).
) satisfy (2.2), (2.4).
Let us show that elements v = { v1, v2, v3, v4} Î  1Ç
1Ç  (
( ) satisfy the additional boundary condition
) satisfy the additional boundary condition
We remark that element w = { w1, 0, Ñg1, 0} belongs to the kernel of  * for an arbitrary g1Î H2(W), g1º 0 in imf450È
* for an arbitrary g1Î H2(W), g1º 0 in imf450È  1È ... È
1È ... È  n1, w1 is a solution of (2.1) with boundary condition (2.5).
n1, w1 is a solution of (2.1) with boundary condition (2.5).
Thus, for { v1, v2, v3, v4} Î  1Ç
1Ç  (
( ) we have
) we have
which implies (2.6).
We arrive at the following assertion.
Theorem 2.1. Suppose that f = { f1, f2, f3, f4} Î M1Ç  (
( ) (j = {j1, j2, j3, j4} Î
) (j = {j1, j2, j3, j4} Î  1Ç
1Ç  (
( )). Then there exists a unique solution {u(x,t), E(x,t), H(x,t)} (v(x,t), F(x,t),Y(x,t)) of (1.2)-(1.5) ((1.6)-(1.9)) with zero boundary conditions such that for all t > 0
)). Then there exists a unique solution {u(x,t), E(x,t), H(x,t)} (v(x,t), F(x,t),Y(x,t)) of (1.2)-(1.5) ((1.6)-(1.9)) with zero boundary conditions such that for all t > 0
Moreover, {u, E, H} ({v,F,Y}) satisfies the additional interface conditions (2.4), where
and
Let f = {f1, f2, f3, f4} Î 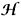 and fn =
and fn =  Î
Î  (
( ), such that
), such that  ® 0 as n ® ¥. Then,
® 0 as n ® ¥. Then,  (t)fn satisfies the following identity
(t)fn satisfies the following identity
where V(t) Î L2(0,T; (
( *)), Vt(t) Î L2(0,T;
*)), Vt(t) Î L2(0,T;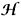 ), V(T) = 0.
), V(T) = 0.
From this we easily obtain that
i.e.,  (t)f is the weak solution of the abstract Cauchy problem
(t)f is the weak solution of the abstract Cauchy problem
We note that  (t) takes M1 into itself. Indeed, if g Î M and V(t) = (T t)g, then from (2.7) it follows that
(t) takes M1 into itself. Indeed, if g Î M and V(t) = (T t)g, then from (2.7) it follows that
Thus,
In the same way we get the corresponding properties for  (t).
(t).
Let us now concern ourselves with the simultaneous boundary observability for a pair of piezoelectric systems. The proof is based on the invariance of the piezoelectric system relative to the one-parameter group of dilations in all variables. This property of the system leads to the following identity:
where g(x) is an arbitrary smooth function, Ñ =  . For g(x) = 21|x x0|2, (2.8) represents a conservation law.
. For g(x) = 21|x x0|2, (2.8) represents a conservation law.
Let f = {f1,f2,f3,f4} Î M1Ç  (
( ) and {u(x,t),E(x,t),H(x,t)} is the corresponding solution of (1.2)-(1.5) with zero boundary conditions.
) and {u(x,t),E(x,t),H(x,t)} is the corresponding solution of (1.2)-(1.5) with zero boundary conditions.
From (2.8) after integration over Wm × (0,T) and summation over m we get
where
m (u,E,H; g) is the restriction of the last three terms on the right-hand side of (2.8) on Wm and
The next assertion is of a technical nature and can be proved by direct computations.
Lemma 2.2. The following representation holds:
Let us now concern ourselves with an estimate of the integral of
m (u, E,H; g) over Wm × (0,T).We consider the elliptic problem
which admits a solution W(x) Î C2(W) Ç C1 ( ).
).
We set
Direct computations give us that (the index m is omitted for simplicity of notations)
We have
where s1 > 0, C0 is such that
and
We note that C(W) > 1/3.
Next, we get the estimate
where s2 is an arbitrary positive number,
We have
Thus, from (2.12)-(2.14) we get the estimate
We now choose s1 and s2. We set
From the inequality (2.15) it follows that
where d is an arbitrary positive number and
From here on we will assume that W and
m satisfy the following conditions: there exists d1> 0 such that
We note that the above conditions are valid when d1 = 0 for star-shaped surfaces  1,
1,  2, ...,
2, ...,  n, and strongly star-shaped surface
n, and strongly star-shaped surface  , i.e.,
, i.e.,
Moreover, if
1, 2,...,
2,..., n are strongly star-shaped with respect to a point x0Î W, then, the above conditions hold with d1 > 0 for a class of domains which includes star-shaped domains.
n are strongly star-shaped with respect to a point x0Î W, then, the above conditions hold with d1 > 0 for a class of domains which includes star-shaped domains.
Henceforth we set
where d1 is defined in (2.17).
Our next goal is to estimate the second integral on the left-hand side of (2.9).
The following inequality is proved by standard arguments
where
c2 > 0 is such that
Now, we are concern with an estimate of the surface integral (over  × (0,T)) in (2.9).
× (0,T)) in (2.9).
Using the boundary conditions (1.5) (Q º G º 0) and additional boundary condition
we get
Let c > 0 be such that
We have
Assume that b = b(x) satisfies the following condition
Thus, from (2.20) we obtain the inequality
from which it follows that
Suppose that the coefficients of the systems (1.2) satisfy the following monotonicity conditions
Using these conditions and Lemma 2.2, we obtain
Thus, from the identity (2.9) and the inequalities (2.16), (2.18), (2.21), (2.23) we get
where
We now consider the problem (1.6)-(1.9) with zero boundary conditions. Let j = {j1, j2, j3, j4} Î  1 Ç
1 Ç  (
( ) and { v,
) and { v, , F, Y} =
, F, Y} =  (t)j.
(t)j.
In this case we have
In the same way we get the estimate
Our next goal is to obtain the simultaneous boundary observation for a pair of systems (1.2), (1.6).
Let f Î M1 Ç  (
( ), j Î
), j Î  1 Ç
1 Ç  (
( ) and
) and
We can immediately verify the identity
The following formula can be proved by direct computations:
We have
We set
Then (2.27) implies the inequality
Henceforth we assume that matrices Aij satisfy the following condition
Taking (2.29) into account, from (2.28) we find that
where
From this and the identity (2.26) we obtain
We multiply (2.24) and (2.25) by
respectively, and add the inequalities thus obtained to (2.30); using the inequality
where
we arrive at the estimate
From (2.31) we deduce the following uniqueness property.
Theorem 2.3. Assume that
m and W satisfy conditions (2.17). Suppose that the matrices , B(m) and the coefficients m(m) satisfy the monotonicity conditions (2.22), satisfy the condition (2.29),
Let f(x) Î M1Ç  (
( ), j(x) Î
), j(x) Î  1Ç
1Ç  (
( ). Suppose that {u(x,t), E(x,t), H(x,t)} and {v(x,t),F(x,t),Y(x,t)} are solutions of problems (1.2)-(1.5) and (1.6)-(1.9) with zero boundary conditions, respectively, and that
). Suppose that {u(x,t), E(x,t), H(x,t)} and {v(x,t),F(x,t),Y(x,t)} are solutions of problems (1.2)-(1.5) and (1.6)-(1.9) with zero boundary conditions, respectively, and that
In this case, if T > T* = T1 +  max
max , then
, then
From Theorem 2.3 it follows that for T > T* the expression
defines a norm on the set of initial data f = {f1,f2,f3,f4} and j = {j1, j2,j3,j4} of problems (1.2)-(1.5) and (1.6)-(1.9) with zero boundary conditions. In (2.32)
We denote by 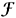 the Hilbert space obtained by completing M1 Ç
the Hilbert space obtained by completing M1 Ç  (
( ) ×
) ×  1 Ç
1 Ç  (
( ) with respect to the norm (2.32). We have
) with respect to the norm (2.32). We have
Our next purpose is to prove simultaneous exact controllability for the problems (1.2)-(1.5), (1.6)-(1.9).
3 Exact controllability
We denote by 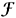 ' the dual space of
' the dual space of 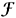 with respect to
with respect to  . Let us consider the pair of problems: (1.2)-(1.4) with boundary conditions
. Let us consider the pair of problems: (1.2)-(1.4) with boundary conditions
and (1.6)-(1.8) with boundary conditions
where Q(x,t), 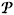 (x,t) Î L2(
(x,t) Î L2( × (0,T)), {f(x),j(x)} Î
× (0,T)), {f(x),j(x)} Î 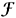 '.
'.
We rewrite systems (1.2) and (1.6) in the form
By definition,
is a solution of (1.2)-(1.4), (3.1) and (1.6)-(1.8), (3.2) if the identity
holds for all { ,
, } Î
} Î 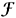 , 0 < t < T. In (3.3)
, 0 < t < T. In (3.3)
In a similar way we define a solution of (1.2), (1.4), (3.1) and (1.6), (1.8), (3.2) with zero data for t = T:
is a solution of (1.2), (1.4), (3.1), (1.6), (1.8), (3.2) with zero data for t = T if
for all { ,
, } Î
} Î 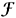 , 0 < t < T.
, 0 < t < T.
Let {g,y} be an arbitrary element of 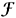 , and let {u,u',E,H,v,v',F,Y} be solution of (1.2), (1.4), (3.1), (1.6), (1.8), (3.2) with zero data for t = T, T > T*, and boundary functions
, and let {u,u',E,H,v,v',F,Y} be solution of (1.2), (1.4), (3.1), (1.6), (1.8), (3.2) with zero data for t = T, T > T*, and boundary functions
where
We set
From (3.4) it follows that
for any { ,
, } Î
} Î 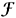 . This implies that M is an isomorphism of
. This implies that M is an isomorphism of 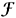 onto the whole of
onto the whole of 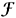 '.
'.
We return to problems (1.2)-(1.4), (3.1) and (1.6)-(1.8), (3.2). Suppose that the initial data {f,j} belong to 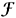 '. We set
'. We set
where
From (3.3) with t = T > T* we find that
for any { ,
, } Î
} Î 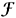 . By (3.5), the right-hand side of the last identity is equal to zero; that is, {u(T), u'(T), E(T), H(T), v(T), v'(T), F(T), Y(T)} generates the zero functional on
. By (3.5), the right-hand side of the last identity is equal to zero; that is, {u(T), u'(T), E(T), H(T), v(T), v'(T), F(T), Y(T)} generates the zero functional on 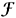 .
.
We arrive at the following assertion.
Theorem 3.1. Assume that
, B(m), m(m), m and W satisfy the conditions of Theorem 2.3. If T > T*, then for any initial data {f,j} Î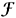 ' of problems (1.2)-(1.5) and (1.6)-(1.9) there exists a control {
' of problems (1.2)-(1.5) and (1.6)-(1.9) there exists a control { (x,t),
(x,t),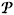 (x,t)} Î C1(0,T;L2(S)) × C0(0,T;L2(S)) such that the corresponding solution of problem (1.6)-(1.9) satisfies
(x,t)} Î C1(0,T;L2(S)) × C0(0,T;L2(S)) such that the corresponding solution of problem (1.6)-(1.9) satisfies
while the vector-valued functions
drive the system (1.2)-(1.5) to a state of rest at the same time T:
To prove this assertion, it suffices to construct functions Q(x,t), 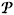 (x,t) as before, by setting
(x,t) as before, by setting
We remark that, in view of the linearity of the systems, it suffices to consider controls that reduce the systems to a state of rest.
Received: 17/IX/02.
Supported by FAPERJ (Brazil), project E-26/151.523/01.
#555/02.
- [1] F. Alabau and V. Komornik, Boundary observability, controllability and stabilization of linear elastodynamic systems, Institut de Recherche Mathématique Avancée, Preprint, Series 15, (1996).
- [2] A. Borrelli and M.C. Patria, Spatial energy estimates in dynamical problems for a semi-infinite piezoelectric beam, Journal of Applied Mathematics, 64 (2000), pp. 73-93.
- [3] G. Duvaut and J.-L. Lions, Les Inéquations en M'ecanique et en Physique, Dunod, Paris, (1972).
- [4] J.N. Eringen and G.A. Maugin, Electrodynamics of continua, Vol. 1, 2 (1990), Berlin, Springer.
- [5] M.A. Horn, Implications of sharp trace regularity results on boundary stabilization of the system of linear elasticity, J. Math. Anal. Appl., 223 (1998), pp. 126-150.
- [6] T. Ikeda, Fundamentals of Piezoelectricity, Oxford, University Press, (1996).
- [7] B.V. Kapitonov, Uniqueness theorem and exact boundary controllability of evolution systems, Siberian Math. J., 34 (1993), pp. 852-868.
- [8] B.V. Kapitonov, Stabilization and exact boundary controllability for Maxwell's equations, SIAM J. Control Optim., 32 (1994), pp. 408-421.
- [9] B.V. Kapitonov, Uniform stabilization and simultaneous exact boundary controllability for a pair of hyperbolic systems, Siberian Math. J., 35 (4) (1994), pp. 722-734.
- [10] B.V. Kapitonov, Simultaneous precise control of systems of linear elasticity, Russian Acad. Sci. Dokl. Math., 48 (2) (1994), pp. 332-337.
- [11] B.V. Kapitonov, Stabilization and simultaneous boundary controllability for a pair of Maxwell's equations, Comp. Appl. Math., 15 (3) (1996), pp. 213-225.
- [12] B.V. Kapitonov, Stabilization and simultaneous boundary controllability for a class of evolution systems, Comp. Appl. Math., 17 (1998), pp. 149-160.
- [13] B.V. Kapitonov, Simultaneous exact controllability for a class of evolution systems, Comp. Appl. Math., 18 (2) (1999), pp. 149-161.
- [14] B.V. Kapitonov and M.A. Raupp, Exact boundary controllability in problems of transmission for the system of electromagneto-elasticity, Math. Meth. Appl. Sci., 24 (2001), pp. 193-207.
- [15] F.A. Khodja and A. Bader, Stabilizability of systems of one-dimensional wave equations by one internal or boundary control force, SIAM J. Control Optim., 39 (6) (2001), pp. 1833-1851.
- [16] K.A. Kime, Boundary controllability of Maxwell's equations in a spherical region, SIAM J. Control Optim., 28 (1990), pp. 294-319.
- [17] V. Komornik, Boundary stabilization, observation and control of Maxwell's equations, Panamer. Math. J., 4 (1994), pp. 47-61.
- [18] J.E. Lagnese, Boundary stabilization of linear elastodynamic systems, SIAM J. Control Optim., 21 (6) (1983), pp. 968-984.
- [19] J.E. Lagnese, Boundary controllability in problems of transmission for a class of second order hyperbolic systems, ESAIM: Control, Optim. and Calculus of Variations, 2 (1997), pp. 343-357.
- [20] J.E. Lagnese, Exact boundary controllability of Maxwell's equations in a general region, SIAM J. Control Optim., 27 (1989), pp. 374-388.
- [21] J.-L. Lions, Contrôlabilité exacte des systémes distribués, C.R. Acad. Sci. Paris, Ser. I Math. 302 (1986), pp. 471-475.
- [22] J.-L. Lions, Exact controllability, stabilization and perturbations for distributed systems, SIAM Rev., 30 (1988), pp. 1-68.
- [23] J.-L. Lions, Contrôlabilité Exacte, Perturbations et Stabilisation des Systčmes Distribués, Tome 1. Contrôlabilite Exacte, Coll. RMA, V. 8 (1998), Masson, Paris.
- [24] P. Martinez, Boundary stabilization of the wave equation in almost star-shaped domains, SIAM J. Control Optim., 37 (3) (1999), pp. 673-694.
- [25] S. Nicaise, Boundary exact controllability of interface problems with singularities. I: addition of the coefficients of singularities, SIAM J. Control Optim., 34 (1996), pp. 1512-1532.
- [26] S. Nicaise, Boundary exact controllability of interface problems with singularities. II: addition of internal control, SIAM J. Control Optim., 35 (1997), pp. 585-603.
- [27] D.L. Russell, Dirichlet-Neumann boundary control problem associated with Maxwell's equations in a cylindrical region, SIAM J. Math. Anal., 24 (1986), pp. 199-229.
- [28] N. Weck, Exact boundary controllability of a Maxwell problem, SIAM J. Control Optim., 38 (2000), pp. 736-750.
Publication Dates
-
Publication in this collection
19 July 2004 -
Date of issue
2003
History
-
Received
17 Sept 2002






























































































































