Abstract
We present optimal upper bounds for the deviation of a fuzzy continuous function from its fuzzy average over [a,b] <FONT FACE=Symbol>Ì</FONT> R, error is measured in the D-fuzzy metric. The established fuzzy Ostrowski type inequalities are sharp, in fact attained by simple fuzzy real number valued functions. These inequalities are given for fuzzy Hölder and fuzzy differentiable functions and these facts are reflected in their right-hand sides.
Fuzzy inequalities; Ostrowski inequality; Fuzzy real analysis
Fuzzy Ostrowski type inequalities
George A. Anastassiou
Department of Mathematical Sciences, University of Memphis, Memphis, TN 38152 U.S.A., E-mail: ganastss@memphis.edu
ABSTRACT
We present optimal upper bounds for the deviation of a fuzzy continuous function from its fuzzy average over [a,b] Ì R, error is measured in the D-fuzzy metric. The established fuzzy Ostrowski type inequalities are sharp, in fact attained by simple fuzzy real number valued functions. These inequalities are given for fuzzy Hölder and fuzzy differentiable functions and these facts are reflected in their right-hand sides.
Mathematical subject classification: 26D07, 26D15, 26E50.
Key words: Fuzzy inequalities, Ostrowski inequality, Fuzzy real analysis.
0 Introduction
Ostrowski inequality (see [8]) has as follows
where f Î C1 ([a,b]), x Î [a,b]. Inequality (*) is sharp, see [1].
Since 1938 when A. Ostrowski proved his famous inequality, see [8], many people have been working about and around it, in many different directions and with a lot of applications in Numerical Analysis and Probability, etc.
One of the most notable works extending Ostrowski's inequality is the work of A.M. Fink, see [6]. The author in [1] continued that tradition.
This current article is mainly motivated by [1], [6], [8], [11] and extends Ostrowski type inequalities into the fuzzy setting, as fuzzyness is a natural reality genuine feature different than randomness and determinism. To the best of our knowledge this is the first attempt of such extension into the fuzzy environment, hoping to find wide continuations and lots of applications.
1 Background
We start with
Definition 1 (see [10]). Let m: 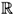 ® [0,1] with the following properties:
® [0,1] with the following properties:
(i) is normal, i.e., $x0Î
; m(x0) = 1.
(ii) m(lx + (1 l)y) > min{m(x), m(y)}, "x,y Î
, "l Î [0,1] (m is called a convex fuzzy subset).
(iii) m is upper semicontinuous on
, i.e., "x0Îand " e > 0, $ neighborhood V(x0): m(x) < m(x0) + e, "x Î V(x0).
(iv) The set
is compact in (where supp(m) := { x Î; m(x) > 0}).
We call m a fuzzy real number. Denote the set of all m with  .
.
E.g.,
{x0}Î , for any x0Î
, for any x0Î 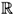 , where
, where 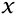 {x0} is the characteristic function at x0.
{x0} is the characteristic function at x0.
For 0 < r < 1 and m Î  define [m]r := { x Î
define [m]r := { x Î 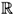 : m(x) > r} and
: m(x) > r} and
Then it is well known that for each r Î [0,1], [m]r is a closed and bounded interval of 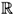 . For u,v Î
. For u,v Î  and l Î
and l Î 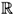 , we define uniquely the sum u Å v and the product l
, we define uniquely the sum u Å v and the product l  u by
u by
where [u]r + [v]r means the usual addition of two intervals (as subsets of 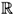 ) and l[u]r means the usual product between a scalar and a subset of
) and l[u]r means the usual product between a scalar and a subset of 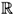 (see, e.g., [10]). Notice 1
(see, e.g., [10]). Notice 1  u = u and it holds u Å v = v Å u, l
u = u and it holds u Å v = v Å u, l  u = u
u = u  l. If 0 < r1< r2< 1 then [u]r2Í [u]r1. Actually [u]r =
l. If 0 < r1< r2< 1 then [u]r2Í [u]r1. Actually [u]r =  , where
, where  Î
Î 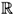 , "r Î [0,1].
, "r Î [0,1].
Define
by
where [v]r =  ; u,v Î
; u,v Î  . We have that D is a metric on
. We have that D is a metric on  . Then (
. Then ( , D) is a complete metric space, see [10], with the properties
, D) is a complete metric space, see [10], with the properties
We need
Lemma 1 (Lemma 2.2 of [5]). For any a,b Î 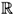 : a,b > 0 and any u Î
: a,b > 0 and any u Î  we have
we have
where õ Î  is defined by õ :=
is defined by õ := 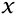 {0}.
{0}.
We also need
Definition 2 (see [10]). Let x,y Î  . If there exists a z Î
. If there exists a z Î  such that x = y + z, then we call z the H-difference of x and y, denoted by z := x y.
such that x = y + z, then we call z the H-difference of x and y, denoted by z := x y.
Definition 3 (Definition 3.3 of [10]). Let T := [x0, x0 + b] Ì 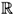 , with b > 0. A function f : T ®
, with b > 0. A function f : T ®  is H-differentiable at x Î T if there exists a f'(x) Î
is H-differentiable at x Î T if there exists a f'(x) Î  such that the limits (with respect to metric D)
such that the limits (with respect to metric D)
exist and are equal to f'(x). We call f' the derivative or H-derivative of f at x. If f is H-differentiable at any x Î T, we call f differentiable or H-differentiable and it has H-derivative over T the function f'.
The last definition was given first by M. Puri and D. Ralescu [9].
We use a particular case of the Fuzzy Henstock integral (d(x) =  ) introduced in [10], Definition 2.1.
) introduced in [10], Definition 2.1.
That is,
Definition 4 (Definition 13.14 of [7], p. 644). Let f : [a,b] ®  . We say that f is Fuzzy-Riemann integrable to I Î
. We say that f is Fuzzy-Riemann integrable to I Î  if for any e > 0, there exists d > 0 such that for any division P = {[u,v];x} of [a,b] with the norms D(P) < d, we have
if for any e > 0, there exists d > 0 such that for any division P = {[u,v];x} of [a,b] with the norms D(P) < d, we have
where å* denotes the fuzzy summation. We choose to write
We also call an f as above (FR)-integrable.
Corollary 1 (Corollary 13.2 of [7]). If f Î C([a,b], ) then f is (FR) integrable on [a,b].
) then f is (FR) integrable on [a,b].
We also need
Lemma 2 (Lemma 1 of [2]). If f,g : [a,b] Í 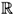 ®
®  are fuzzy continuous (with respect to metric D), then the function F : [a,b] ®
are fuzzy continuous (with respect to metric D), then the function F : [a,b] ® 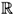 +È {0} defined by F(x) := D(f(x), g(x)) is continuous on [a,b], and
+È {0} defined by F(x) := D(f(x), g(x)) is continuous on [a,b], and
We mention
Lemma 3 (Lemma 3 of [2]). Let f : [a,b] Í 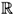 ®
®  be fuzzy continuous. Then
be fuzzy continuous. Then
We use the Fuzzy Taylor formula.
Theorem 1 (Theorem 1 of [2]). Let T := [x0 ,x0 + b] Ì 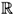 , with b > 0. We assume that f(i) : T ®
, with b > 0. We assume that f(i) : T ®  are H-differentiable for all i = 0,1,...,n 1, for any x Î T. (I.e., there exist in
are H-differentiable for all i = 0,1,...,n 1, for any x Î T. (I.e., there exist in
 such that the limits in D-distance exist and
such that the limits in D-distance exist and
for all i = 0,1,...,n 1.) Also we assume that f(n), is fuzzy continuous on T. Then for s > a, s,a Î T we obtain
where
Here Rn(a,s) is fuzzy continuous on T as a function of s.
We use
Proposition 1 (Proposition 1 of [4]). Let F(t) := tn
u, t > 0, n Î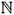 , and u Î
, and u Î  be fixed. Then (the H-derivative)
be fixed. Then (the H-derivative)
In particular when n = 1 then F'(t) = u.
We mention
Proposition 2 (Proposition 6 of [4]). Let I be an open interval of
and let f : I ® be H-fuzzy differentiable, c Î
be H-fuzzy differentiable, c Î 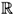 . Then
. Then
We use the "Fuzzy Mean Value Theorem".
Theorem 2 (Theorem 1 of [4]). Let f : [a,b] ®  be a fuzzy differentiable function on [a,b] with H-fuzzy derivative f' which is assumed to be fuzzy continuous. Then
be a fuzzy differentiable function on [a,b] with H-fuzzy derivative f' which is assumed to be fuzzy continuous. Then
for any c,d Î [a,b] with d > c.
We finally need the "Univariate Fuzzy Chain Rule".
Theorem 3 (Theorem 2 of [4]). Let I be a closed interval in
. Here g : I ® z := g(I) Í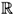 is differentiable, and f : z ® is H-fuzzy differentiable. Assume that g is strictly increasing. Then (f ° g)'(x) exists and
is differentiable, and f : z ® is H-fuzzy differentiable. Assume that g is strictly increasing. Then (f ° g)'(x) exists and
2 Results
We give the following
Theorem 4. Let f Î C([a,b] , ), the space of fuzzy continuous functions, x Î [a,b] be fixed. We assume that f fulfills the Hölder condition
), the space of fuzzy continuous functions, x Î [a,b] be fixed. We assume that f fulfills the Hölder condition
for some Lf > 0. Then
Proof. We have that
Optimality of (1) comes next.
Proposition 3. Inequality (1) is sharp, in fact, attained by f*(y) := |y x|a u, 0 < a<1, with u Î
u, 0 < a<1, with u Î  fixed. Here x,y Î [a,b].
fixed. Here x,y Î [a,b].
Proof. Clearly f*Î C([a,b], ): for letting yn ® y, yn Î [a,b], then
): for letting yn ® y, yn Î [a,b], then
Furthermore
That is, for Lf* := D(u,õ) we get
So that f* is a Hölder function.
Finally we have
Next comes the basic Ostrowski type fuzzy result in
Theorem 5. let f Î C1([a,b], ), the space of one time continuously differentiable functions in the fuzzy sense. Then for x Î [a,b],
), the space of one time continuously differentiable functions in the fuzzy sense. Then for x Î [a,b],
Inequality (2) is sharp at x = a, in fact attained by f*(y) := (y a)(b a)  u, u Î
u, u Î  being fixed.
being fixed.
Proof. We observe that
proving (2).
By Propositions 1, 2 and Theorem 3 we get that f*'(y) = (b a)  u. We have that
u. We have that
And
That is equality in (2) is attained.
We conclude with the following Ostrowski type inequality fuzzy generalization in
Theorem 6. Let f Î Cn+1([a,b], ), n Î
), n Î 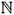 , the space of (n + 1) times continuously differentiable functions on [a,b] in the fuzzy sense. Call
, the space of (n + 1) times continuously differentiable functions on [a,b] in the fuzzy sense. Call
Then
If f(i)(a) = õ, i = 1,...,n. Then
Inequalities (3) and (4) are sharp, in fact attained by
 being fixed.
being fixed.
Corollary 2. Let f Î C2([a,b], ). Then
). Then
When f'(a) = õ, then
Proof of Theorem 6. Let x Î [a,b], then by Theorem 1 we get
where
(here we need x > a). We observe that
We have established inequalities (3) and (4).
Consider g(x) := 
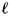 Î
Î 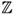 +, u Î
+, u Î  fixed. We prove that g is fuzzy continuous. Let xn Î [a,b] such that xn ® x as n ® +¥. Then
fixed. We prove that g is fuzzy continuous. Let xn Î [a,b] such that xn ® x as n ® +¥. Then
Hence by the last argument, Propositions 1, 2 and Theorem 3 we obtain that f*Î Cn+1([a,b], ).
).
We see that
That is M = 0. Furthermore it holds
Finally, we notice that
Also we find
Proving (3) and (4) sharp, in fact attained inequalities.
Received: 19/IX/02.
#556/02.
- [1] George A. Anastassiou, Ostrowski type inequalities, Proc. AMS, 123 (1995), 3775-3791.
- [2] George A. Anastassiou, Rate of convergence of Fuzzy neural network operators, univariate case, accepted in Journal of Fuzzy Mathematics.
- [3] George A. Anastassiou, Univariate fuzzy-random neural network approximation operators, submitted.
- [4] George A. Anastassiou, On H-fuzzy differentiation, accepted in Mathematica Balkanica, (2002).
- [5] George A. Anastassiou and Sorin Gal, On a fuzzy trigonometric approximation theorem of Weierstrass-type, in Journal of Fuzzy Mathematics, 9, No. 3 (2001), 701-708.
- [6] A.M. Fink, Bounds on the deviation of a function from its averages, Czechoslavak Math. J., 42 (117) (1992), 289-310.
- [7] S. Gal, Approximation theory in fuzzy setting, Chapter 13 in Handbook of Analytic Computational Methods in Applied Mathematics (edited by G. Anastassiou), Chapman & Hall, CRC Press, Boca Raton, New York, 2000, pp. 617-666.
- [8] A. Ostrowski, Über die Absolutabweichung einer differentiebaren Funktion von ihrem Integralmittelwert, Comment. Math. Helv., 10 (1938), 226-227.
- [9] M.L. Puri and D.A. Ralescu, Differentials of fuzzy functions, J. of Math. Analysis and Appl., 91 (1983), 552-558.
- [10] Congxin Wu and Zengtai Gong, On Henstock integral of fuzzy number valued functions (I), Fuzzy Sets and Systems, 120, No. 3 (2001), 523-532.
- [11] L.A. Zadeh, Fuzzy sets, Information and Control, 8 (1965), 338-353.
Publication Dates
-
Publication in this collection
19 July 2004 -
Date of issue
2003
History
-
Received
19 Sept 2002














































