Macroscopic modeling of columnar dendritic solidification

Macroscopic modeling of columnar dendritic solidification

B. Goyeau^I; P. Bousquet-Melou^{I, II}; D. Gobin^I; M. Quintard^III; F. Fichot^II

^ILaboratoire FAST, Universités Paris VI et Paris XI, UMR CNRS 7608 Bât. 502, Campus Universitaire, 91405 Orsay Cedex, France E-mails: [e-mail] / [e-mail]

^IIInstitut de Radioprotection et de Sureté Nucléaire, Bât 700, CEA Cadarache, 13106 Saint Paul lez Durance, France E-mails: [e-mail]

^IIIInstitut de Mécanique des Fluides de Toulouse Avenue du Professeur Camille Soula, 31400 Toulouse, France E-mails: [e-mail]

ABSTRACT

This paper deals with the derivation of a macroscopic model for columnar dendritic solidification of binary mixtures using the volume averaging method with closure. The main originalities of the model are first related to the explicit description of evolving heterogeneities of the dendritic structures and their consequences on the derivation of averaged conservation equations, where additional terms involving porosity gradients are present, and on the determination of effective transport properties. These average properties are defined by the associated closure problems taking into account the geometry of the dendrites and the local intensity of the flow. The macroscopic solute transport is obtained by considering macroscale non-equilibrium giving rise to macroscopic dispersion and interfacial exchange phenomena. Mass exchange coefficients are accurately explicited as a function of the local geometry.

Mathematical subject classification: 76S05, 76T05, 76R05.

Key words: columnar solidification, macroscopic model, volume averaging, closure problems.

1 Introduction

Macroscopic modeling of dendritic solidification has been the subject of intense research activity in the last decades [1-3] and one of the most important challenging improvement lies in an accurate micro-macroscopic description of transport phenomena within the dendritic mushy zone. In most averaged representations, this region is described as a porous medium and macroscopic conservation equations have been obtained using the mixture theory [4-6] or up-scaling procedures [1, 7-11]. Due to its ability to incorporate complex microscopic information in averaged equations and effective transport properties (permeability, conductivity, mass diffusion coefficients, ...), the method of volume averaging has been often chosen for the derivation of the macroscopic models [12-20].

This technique considers a representative volume averaging within the porous region. The local conservation equations are integrated over this volume providing averaged macroscopic transport equations valid in the whole domain [21, 22]. Phase interaction terms at the solid-liquid interface arise from the averaging process leading to several interfacial area integrals.

Although a columnar dendritic mushy zone is characterized by continuous spatial evolution of its geometry, the method of volume averaging has been used without dealing with this difficulty. Furthermore, due to the complex shape of the interfaces, phase interaction integral terms which are generally related to effective properties are not explicitly calculated in these models and are represented by semi-empirical laws. However, some experimental and numerical investigations have been carried out in order to improve the momentum transport description. They propose a more realistic spatial description of the permeability tensor in columnar structures than the very schematic Kozeny-Carman relationship [12-15, 17, 19, 23, 24] but the conclusions show that more data and theoretical developments are still necessary.

Despite their strong influence during solid-liquid phase change, very little attention has been paid to an accurate description of effective conductivity and solute diffusion-dispersion coefficients in the energy and species conservation equations. In this latter case, characterized by very different molecular diffusion coefficients in the liquid and solid phases, the mass diffusion rate in the solid phase is generally assumed to be extremely fast (lever rule) or very slow (Scheil’s behavior). The Scheil’s model assumes no mass exchange at the solid/liquid interface and generally the effective mass diffusion coefficient only depends on the liquid volume fraction although tortuosity of the micro-structure and local dispersion phenomena can have a strong influence on the macroscopic solute transport [25].

A significant improvement has been performed in this direction by Beckermann and co-authors [9, 10] who proposed a three-phase macroscopic solute diffusion model where interfacial species fluxes in phase k are proportional to the difference between the interfacial and volume-averaged concentration such as j_k = h_k ( - áC_k ñ^k ), h_k being the mass exchange coefficient. This latter coefficient is found to be mainly dependent on the solute diffusion length [10] while it is actually strongly related to the location within the dendritic layer and therefore to tortuosity and local dispersion phenomena [26].

This brief review shows that the above-mentioned representation has still to be refined in order to more accurately include local geometry and phenomena (tortuosity, local dispersion, interfacial exchanges, ...) at the macroscopic level. The objective of this paper is to improve the micro-macroscopic description of the transport processes in columnar dendritic structures by using the volume averaging method with closure problems. According to Wang and Beckermann [10] and Quintard and Whitaker [27] for soil contamination problems, solute transport is based on a macroscale non-equilibrium description leading to a macroscopic representation of interfacial species exchange (active dispersion). All the interfacial area integrals arising from the averaging procedure are explicited and the associated closure problems are derived for the determination of effective transport properties. Influence of evolving heterogeneities is discussed at the different scale of the up-scaling process.

2 The procedure of volume averaging

The macroscopic conservation equations are derived using a volume averaging procedure [28] whose main theorems are recalled in ^{Appendix A}.

2.1 Local conservation equations

We consider a columnar dendritic mushy zone and the local averaging volume V represented in Figure 1, where r₀ is the radius of V and l_b stands for the interdendritic characteristic length. The convective flow of the liquid mixture (b-phase) through this dendritic mushy layer is assumed to be laminar and incompressible while the transport of the solid phase (s-phase) is not considered (v_s = 0). All physical properties of the mixture are assumed to be constant and the Boussinesq approximation to apply. The local problem describing the mass, momentum, solute and energy conservation in both phases of the averaging volume V is thus given by:

where v_b is the liquid velocity, and C_k and H_k (k = b, s) are the mass fraction of a p-constituent and the mass enthalpy in the k-phase, respectively. The mass and heat fluxes are respectively defined by J_k = -r_k

_kÑ C_k and q_k = - l_kÑ T_k for k = b, s. The conservation of mass, momentum solute and energy at the solid-liquid interface A_bs are respectively given by:

where w_bs is the velocity of the interface A_bs and n_bs is the unit normal vector pointing from the b-phase to the s-phase. Thermodynamical equilibrium is considered at A_bs and the local coupling between solid and liquid temperatures (T_s and T_b) and concentration is obtained through the functions g_s and g_b that describe the solidus and liquidus lines of the equilibrium phase diagram:

Finally, if A_ke refers to the area of entrances and exits of the k-phase in V (Figure 1), the boundary conditions at A_ke are:

where the functions

_v,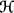 _k and _k (k = b, s) are unknown at this stage. The discussion concerning the nature of these functions will take place in section 3.

2.2 Geometrical considerations

The volume averaging method is an up-scaling method generally used for systems where the separation between the characteristic length scale is satisfied [21]. In columnar dendritic structures, averaged properties are actually continuously space-dependent and therefore scale separation depends on the spatial evolution of the geometry (decreasing rate of the geometry t) [23]. Three length scale constraints have been identified (Table 1).

For small evolving heterogeneities, the dendritic layer can be viewed as homogeneous and therefore averaged properties are constant whatever the size of the averaging volume. For large t, scale separation is not satisfied, and more theoretical work is needed to explore alternative descriptions using for instance deforming averaging volume [29] or jump boundary condition [30-32]. Between these two limiting situations, i.e. for ‘‘moderate’’ evolving heterogeneities, Goyeau et al. [23] show that, although less clear-cut, scale separation remains satisfied since:

Under this condition, the averaging procedure can still be used but two difficulties arise. First, the averaged properties are not only point-dependent but also depend on the size of the averaging volume. Second, as shown later, porosity gradients explicitly appear both in the macroscopic conservation equations and in the associated closure problems giving rise to a very complex closure analysis (section 3).

2.3 Averaged equations

Keeping in mind condition (18), we now apply the classical averaging theorems to the system (1)-(14) after introducing Gray’s decomposition [33]:

where áY_kñ^k and _k represent the intrinsic average and the deviation of the generic quantity Y in the k-phase, respectively. áY_kñ^k is obtained by using definition (A.3). This leads to the following non-closed macroscopic equations.

2.3.1 Mass and momentum equations

Averaging the mass balance at the solid-liquid interface equation (8) gives rise to:

where

_k is the melting (k = b) or the solidification (k = s) rates defined by:

Beside the absence of solid transport, we consider that the local solid velocity v_s due to dilatation is very small compared to the interface velocity w_bs and will be neglected in this analysis. Therefore, the averaged mass conservation equation for the mixture takes the final form:

while averaging Navier-Stokes equation (3) leads, after simplifications, to the non-closed averaged momentum equation:

2.3.2 Concentration equations

As previously said, one originality of the present model lies in the macroscale non-equilibrium description of the solute transport. In other words, the solute transport is described separately in the liquid and solid phases and no particular assumption is retained concerning the solute diffusion in the solid phase. Interfacial solute exchange due to the difference between interfacial- and volume-averaged concentrations in both phases are explicitly included in the analysis. Averaging equations (4) and (5) leads to the non-closed macroscopic equations for solute transport in the solid and liquid phases:

2.3.3 Energy equations

Similarly, averaging equations (6) and (7) leads the non-closed energy conservation equations:

Since the Lewis number (ratio of the thermal to the mass diffusivity) is high for metallic alloys (Le ~ 10⁴), the liquid and solid phases are in thermal equilibrium [2] and only one averaged energy equation can be used since áT_bñ^b ~ áT_sñ^s ~ áT ñ [34, 35]. Therefore, adding equations (26) and (27) and taking into account the boundary condition (10), a single non-closed energy equation is obtained:

where áH ñ = (e_b r_b áH_bñ^b + e_s r_s áH_sñ^s) / árñ represents the enthalpy of the mixture. Rigourously, equations (23)-(28) have been obtained after discarding numerous geometrical moments that have been shown to be very small in dendritic structures [23]. Let us only recall that the main consequence of this simplification is that the averaged quantities can be extracted from area integrals.

In equations (23)-(25) and (28), the area integral terms involving the deviation quantities are actually related to effective transport properties of the dendritic mushy zone. In order to derive a closed form of these equations, the associated closure problems have to be written to express the deviation fields

_k in terms of intrinsic averaged quantities áY_kñ^k.

3 Closure

The first step of the derivation of closure problems is performed by using the Gray’s decomposition in the local conservation equations (1)-(7) and by subtracting the non-closed averaged equations (23)-(25) and (28). This gives rise to a very complex set of deviation equations which can be simplified first by comparing the order of magnitude of the different terms on the basis of the length scale constraint (16), and second, by allowing for the following physical considerations:

(i) The volume change parameter (shrinkage or expansion) is small and brings no contribution to the interdendritic flow [1, 8].

(ii) The solidification process is slow enough to consider that the interface growth velocity is small compared to the average liquid velocity [36].

(iii) The time scales separation is satisfied and the deviation problems can be treated as quasi-steady [27].

(iv) Temperature and concentration at the interface can be decoupled at the closure-problem level [26].

The derivation of closure problems for homogeneous structures does not raise any major difficulty but the presence of evolving heterogeneities makes this derivation more complex. It order to illustrate this, let us consider the boundary value problem for deviations

_b and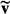 _b, which, after straightforward manipulations, takes the form:

We are here confronted to three difficulties. First, in equations (30) and (31), the terms involving intrinsic average velocity and porosity gradients can be identified as source terms since they generate the deviations fields. The spatial porosity dependence actually means that we are dealing with a non-local closure problem since pressure and velocity deviations not only depend on the local geometry of the averaging volume but also on macroscopic spatial variations of averaged properties. In that case, looking for a solution for _b and 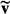_b would impose a relation of the type:

where is therefore related to the closure variables whose determination remains an extremely complicated task needing more theoretical developments. However, if we consider the length scale constraint (18), we can estimate that the two last terms in equation (30) are small compared to the area integral friction term, leading to a classical boundary value problem [37]. This is obviously an approximation since, due to evolving heterogeneities, (18) is not valid everywhere along the dendrites. The second difficulty concerns the nature of _v(r,t) at A_be. For homogeneous porous media, the boundary value problem is generally solved in a representative region (unit cell) with periodicity conditions for pressure and velocity. In dendritic structures, a flow rate conservation condition would be probably more realistic. Nevertheless, it is known that the boundary condition (32) influences the deviation fields only on a region of thickness l_b at the boundary of the averaging volume [37]. Finally, unlike homogeneous porous media, averaged properties in dendritic structures not only depend on the location of the averaging volume but also depend on the size of this latter. Actually, this dependence is directly related to the decreasing rate of the structure geometry. For moderate evolving heterogeneities, it has been shown that a common range for r₀ exists where effective transport properties are rather constant [23, 24]. Taking into account the above assumptions, the simplified problems for momentum, concentration and temperature deviations are finally given by:

Momentum

Concentration

Temperatures

where in condition (40) represents the average concentration in the k-phase at the interface. In the above system, let us recall that we require á_kñ^k = 0, where _k represents a generic deviation field. The form of the macroscopic source terms in equations (36), (39), (40) and (44) generating the deviations 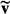_b, _b, _k and _k (k = b, s), respectively, suggests that they can be written as [26, 27, 36, 37]:

where M, m, a_k, and e_k are the closure variables solutions of the periodic problems which are obtained by introducing deviations (47)-(51) in the deviations problems (34)-(46). Since the closure problem (34)-(37) is non linear, it has been shown that the closure variable M can be separated into a linear and inertia contributions, the former being related to the permeability tensor while the second one is related to the Forchheimer coefficient [37]. For conciseness, the set of periodic boundary closure problems are not detailed here, all the details being available in the following references [26, 36-40].

4 Closed form of the macroscopic model

According to assumptions (i)-(iv) and solutions (47)-(51), the final form of the macroscopic model for solidification of columnar dendritic mushy zone can be written:

where the velocity is written in term of superficial velocity (filtration). The solidification rate present in equations (52),(54) and (55) is obtained by averaging the boundary condition (9) to give:

In equations (53)-(56), K, F, D_b, L_eff and h_mk (k = b, s) represent the effective transport properties of the dendritic structure which are obtained after numerical determination of closure variable fields. In the momentum equation (53), K is the permeability tensor that depends on the tortuosity of the porous structure while F represents the Forchheimer correction tensor which accounts for the local inertia effects. Since the closure variables M and m in (47) and (48), respectively, have been decomposed in order to separate linear friction and inertia effect such as M = R + S and m = r + s [37], K and F can be explicitly written under the form:

At this stage, the numerical solution of the closure problem for variables S and s associated with the Forchheimer coefficient still remains a challenge. D_b in equation (55) represents the effective diffusion dispersion tensor given by:

while the effective conductivity in equation (56) is:

Finally, in equations (54) and (55) the interfacial mass exchange due to macroscale non-equilibrium is represented by two terms involving mass exchange coefficients h_mk (k = b, s) whose dependence to the local geometry is given by:

5 Discussion and conclusion

The comparison of the above macroscopic columnar dendritic solidification model with the existing ones [2, 3] leads to emphasize the following main characteristics. First, as shown in expressions (58)-(62) all the effective transport properties, instead of being given by empirical constitutional relations, are derived from closure problems which take into account the micro-geometry of the structure (tortuosity) but also, local inertia and dispersion phenomena. The second characteristic is related to macroscale non equilibrium for the solute transport where macroscopic interfacial mass exchange explicitly arise from the up-scaling procedure. These macroscopic terms are similar to those introduced by Ni and Beckermann [9], but in the present model, coefficients h_mk are accurately obtained by solving the associated closure problem [26]. In the latter reference, Bousquet-Melou et al. show that these coefficients are strongly dependent on the structure, the location and the flow intensity in the mushy zone. Furthermore, due to evolving heterogeneities, most averaged conservation equations include additional terms involving explicit porosity gradients such as, for instance, the second Brinkman correction term in the momentum equation (53). Although they can be considered as second order terms, all of them have to be quantified in the context of solidification before any conclusion concerning their contribution on macroscopic transport phenomena may be drawn. Finally, it can be seen in equations (55) and (57) that other additional terms involving u_b and d_b are included. Actually, these coefficients given by:

can be viewed as velocity-like vectors that contribute to macroscopic convective solute transport [27, 41, 42]. According to results obtained in the context of soil contamination, these terms are not necessarily negligible since they have been found to represent about 10% of the global convective transport [27].

In conclusion, the derivation of this solidification model using the method of volume averaging with closure has allowed us to provide a more complete macroscopic description of transport phenomena, improving the micro-macro interactions both in the definition of average transport properties and conservation equations. Numerical calculations are presently under development in order to quantify the relevance of such a model.

Nomenclature

A _bs

interfacial area of the b-s interface within the macroscopic region, m².

A_ke

area of entrances and exits for the k-phase within the macroscopic system, m².

C_k

concentration in the k-phase, wt pct.

average concentration at the interface, wt pct.

_k

molecular diffusivity of the k-phase, m² s^-1.

D _b

effective solute dispersion tensor, m² s^-1.

d _b

a velocity vector-like coefficient, ms^-1.

F

Inertia tensor

g

gravitational acceleration, m.s^-2.

h_mk

mass exchange coefficient, s^-1.

H_k

enthalpy in the k-phase.

I

unit tensor.

K

permeability tensor, m²

L

general characteristic lengh for volume averaged quantities, m.

l _b

interdendritic lengh scale and size of the unit cell, m.

l_i

i= 1,2,3 lattice vectors, m.

_k

phase change rate, kg m^-3 s^-1.

n _bs

unit normal vector pointing from the b-phase toward the s-phase.

P _b

pressure in the b-phase, Pa.

r ₀

size of the averaging volume, m.

T_k

Temperature in the k-phase , K.

t

time, s

time scale for deviation quantity, s

t ^*

time scale for average quantity, s

u _b

a velocity vector-like coefficient, ms^-1.

V

averaging volume, m³.

V_k

volume of the k-phase within V, m³.

v _b

velocity vector in the b-phase, ms^-1.

áv_bñ

superficial averaged velocity, ms^-1.

w _bs

interface velocity vector, ms^-1.

Greek Letters

e_k

k-phase volume fraction.

L_eff

Effective conductivity, W m^-1 K^-1.

m_b

dynamic viscosity of the b-phase, Pa.s.

_k

spatial deviation of the quantity Y_k.

áY_kñ^k

intrinsic average of the quantity Y_k .

r_k

k-phase density, Kg m^-3.

Subscripts

b

liquid phase

s

solid phase

Received: 14/IV/03. Accepted: 24/III/04.

#569/03.

If we consider a physical quantity Y_b associated to the b-phase, the superficial volume average of Y_b in the averaging volume V (Figure 1) is given by:

where V_b is the volume of the b-phase contained within the averaging volume. In most cases, the intrinsic phase average of Y_b is more representative and is defined by:

Therefore,superficial and intrinsic averages are related by:

where e_b is the b-phase volume fraction.

Finally, averaged conservation equations can be obtained by using spatial and temporal partial derivative theorems given by [21]:

where w_bs is the interface velocity and n_bs is the unit normal vector at the solid-liquid interface (Figure 1) [21].

• [1] C. Beckermann and R. Viskanta, Applied Mechanics Review 46 (1) (1993), 1-27.
• [2] C. Beckermann and C.Y. Wang, Annual Review of Heat Transfer 6 (1995), 115-198.
• [3] P.J. Prescott and F.P. Incropera, Adv. in Heat Transfer 28 (1996), 231-338.
• [4] R.N. Hills, D.E. Lopper and P.H. Roberts, Q.J. Mech. appl. Math. 36 (1983), 505-539.
• [5] W.D. Bennon and F.P. Incropera, Int. J. Heat Mass Transfer 30 (10) (1987), 2161-2170.
• [6] P.J. Prescott, F.P. Incropera and W.D. Bennon, Int. J. Heat Mass Transfer 34 (9) (1991), 2351-2359.
• [7] C. Beckermann, Melting and solidification of binary mixtures with double-diffuse convection in the melt, Ph.D. thesis, Purdue University, West Lafayette (1987).
• [8] S. Ganesan and D.R. Poirier, Metallurgical Transactions 21B (1990), 173-181.
• [9] J. Ni and C. Beckermann, Met. Trans. 22B (1991) 349-361.
• [10] C.Y. Wang and C. Beckermann, Met. Trans. A 24A (1993) 2787-2802.
• [11] C.Y. Wang and C. Beckermann, Metallurgical and Material Transactions A 27A (1996), 2754-2764.
• [12] N. Streat and F. Weinberg, Met. Trans. B 7B (1976), 417-423.
• [13] K. Murakami, A. Shiraishi and T. Okamoto, Acta metall. 31 (1983), 1417-1424.
• [14] R. Nasser-Rafi, R. Deshmukh and D.R. Poirier, Met. Trans. 16A (1985), 2263-2271.
• [15] D.R. Poirier, Met. Trans. 18B (1987), 245-255.
• [16] C. Beckermann and R. Viskanta, Physico Chemical Hydrodynamics, 10 (1988), 195-213.
• [17] S. Ganesan, C.L. Chan and D.R. Poirier, Materials Science and Engineering A151 (1992), 97-105.
• [18] D.R. Poirier and P. Ocansey, Materials Sciences and Engineering A171 (1993), 231-240.
• [19] M.S. Bhat, D.R. Poirier and J.C. Heinrich, Metallurgical and Materials Transactions B 26B (1995), 1049-1056.
• [20] M.C. Schneider and C. Beckermann, Int. J. Heat Mass Transfer 38 (18) (1995), 3455-3473.
• [21] S. Whitaker, Ind. Eng. Chem. 12 (1969), 12-28.
• [22] J. Bear, Dynamics of Fluids in Porous Media, Dover, (1972).
• [23] B. Goyeau, T. Benihaddadene, D. Gobin and M. Quintard, Transport in Porous Media 28 (1997), 19-50.
• [24] B. Goyeau, T. Benihaddadene, D. Gobin and M. Quintard, Metallurgical and Materials Transactions B 30B (1999), 613-622.
• [25] A. Neculae, B. Goyeau, M. Quintard and D. Gobin, Mat. Eng. Sciences A 323 (2002), 367-376.
• [26] P. Bousquet-Melou, A. Neculae, B. Goyeau and M. Quintard, Metallurgical and Materials Transactions B 33B (2002), 365-376.
• [27] M. Quintard and S. Whitaker, Advances in Water Resources 17 (1994), 221-239.
• [28] S. Whitaker, The Method of Volume Averaging, Vol. 13, Kluwer Academic Publishers, 1999.
• [29] J. Cushman, Water Resources Research 20 (11) (1984), 1668-1676.
• [30] J.A. Ochoa-Tapia and S. Whitaker, Int. J. Heat Mass Transfer 38 (1995), 2635-2646.
• [31] J.A. Ochoa-Tapia and S. Whitaker, Int. J. Heat Mass Transfer 38 (1995), 2647-2655.
• [32] J.A. Ochoa-Tapia and S. Whitaker, Int. J. Heat Mass Transfer 40 (1998), 2691-2707.
• [33] W.G. Gray, Chem. Eng. Sci. 3 (1975), 229-233.
• [34] S. Whitaker, Transport in Porous Media 1 (1986), 3-35.
• [35] M. Quintard and S. Whitaker, Int. J. Heat Mass Transfer 38 (15) (1995), 2779-2796.
• [36] P. Bousquet-Melou, B. Goyeau, M. Quintard, F. Fichot and D. Gobin, Int. J. Heat Mass Transfer 45 (2002), 3651-3665.
• [37] S. Whitaker, Transport in Porous Media 25 (1996), 27-61.
• [38] M. Quintard, M. Kaviany and S. Whitaker, Advances Water Resources 20 (2-3) (1997), 77-94.
• [39] P. Bousquet-Melou, Modélisation macroscopique et simulation numérique de la solidification des mélanges binaires, Ph.D. thesis, University of Paris 6 (2000).
• [40] C. Moyne, S. Didierjean, H.P. Amaral-Souto and O.T. da Silveira, Int. J. Heat Mass Transfer 43 (2000), 3853-3867.
• [41] M.A. Paine, R.G. Carbonell and S. Whitaker, Chem. Engng Sci. 38 (1983), 1781-1793.
• [42] D.A. Edwards, M. Shapiro and H. Brenner, Phys. of Fluids 5 (4) (1993), 837-48.

Appendix A  - Volume-averaging definitions

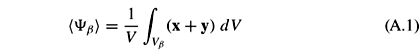
Publication Dates

• Publication in this collection
  11 July 2005
• Date of issue
  Dec 2004

History

• Accepted
  24 Mar 2004
• Received
  14 Apr 2003