Weak solutions for the electrophoretic motion of charged particles

Weak solutions for the electrophoretic motion of charged particles

Luciano Bedin^I; Mark Thompson^II

^IDepartament of Mathematics, UFSC, Trindade, 88040-900 Florianópolis, SC. E-mail: [e-mail]

^IIDepartament of Pure and Applied Mathematics, IM, UFRGS, Av. Bento Gonçalves 9500, 91509-900 Porto Alegre, RS. E-mail: [e-mail]

ABSTRACT

We introduce a weak formulation for a system of electrostatic and hydrodynamic equations modelling the electrophoretic motion of charged particles in ionized fluids. We obtain a local in time existence theorem, using the results established in [11] and properties of the solutions of the Poisson-Boltzmann equation. These properties follows from singular integral operators techniques.

Mathematical subject classification: 35J60, 92C05, 35J50, 42B20.

Key words: Poisson-Boltzmann equation, singular integral operators, Stokes problem, electrophoresis.

1 Introduction

In this paper we establish results on existence and uniqueness of the weak solutions for a system modelling the motion of a charged particle driven by the action of an external electrical field. This phenomena is known as electrophoresis and is important in many technical applications (a vast literature is available: see for example [29], [24], [27], [2], [1], [3], [13], [30], [14]).

We are considering a particle (a charged polymer, for example) immersed in an ionized solution (a viscous incompressible fluid). On the boundary of the enclosure an external electric field induces the electrical potential inside the enclosure which is determined by the Poisson-Boltzmann equation (see [19], [10]). The hydrodynamic behavior of the system is governed by the Navier-Stokes equation.

We are not considering the usual approximation for the effect of the electrical field on the particle based on Prandtl boundary layer theory well known in colloid science, the so called slip-velocity condition (for details see [4], [22], [27]); their derivation requires better regularity properties of the boundary of the particle (see [28] and the discussion in the introduction of [27]).

As remarked in [24] the theoretical analysis of the electrophoretic motions is quite difficult, as it combines specific features of polymer physics with the intrinsic complexity of electrokinetic phenomena. From a mathematical standpoint the difficulties reside in the treatment of the electrical-hydrodynamic couple and on the low regularity of the data. We have established elsewhere [6] the existence of a H¹-variational solution for the electrostatic potential, for a general class of domains. In the case of Lipschitz regions we have established a H^3/2-regularity result by means of the singular integral operators theory; this regularity is optimal, even in C¹-domains (see the comments and negative results in [20]). For C^1,a-domains, 0 < a < 1, and suitable charge distribution this theory can be applied in the classical sense ([25], [18], [7]) in order to obtain more regularity for the potential [5].

Recently, the motion of rigid bodies in a bounded domain filled with a viscous flow has been treated rigorously ([11], [17]). Special techniques (from the transport theory [23]) have been used in order to obtain existence and properties of the suitable weak solutions for these systems. In particular in [11] a global weak formulation is introduced and existence of solutions local in time is established when a L² body force and C^1,1-domains are considered. Evidently, in the study of the electrophoretic motion we can not use directly these results because we have an external electrical field interacting with the ionized solution. However, we obtain a similar result of local existence (see Theorem 3.1); this is obtained as a consequence of uniform bounds and convergence properties involving the electrical force term F (Corollary 4.1, Theorem 4.2). Following the discussion in [6] we choose to prove these properties restricted to the case which the surface charge distribution of the particle and the fixed charge distribution (in the particle and in the solution) are L² and L^¥ functions, respectively; in this case we need only consider the Lipschitz regularity on the boundary of the particle. The existence of weak solutions obtained in Theorem 3.1 follows from the additional hypothesis that the particle domain is of class C^1,1. More properties on F can be obtained in the C^1,a context if we assume stronger hypotheses [5] on the charge distributions but we do not consider this situation in this paper.

2 The governing equations

Consider a rigid, charged particle immersed in a electrolyte solution under the action of an external electrical field. We suppose that the solution (a viscous fluid) occupies a region D Ì ³ and at the initial moment of time, the particle (a rigid body) occupies a compact region ₀Ì D such that its center of mass is located at the origin y = 0 of a Cartesian coordinates y.

Let us define K(t) as the domain occupied by the particle in the time t and f(x,t) as a real valued function which represents the electrical potential in (x,t) Î D × [0,T], where "t Î [0,T], dist(¶D;¶K(t)) > d, where d is a fixed constant. We set y(x,t) = , where L is the temperature (constant) of the system and e is the electron charge. The governing equations and boundary conditions to y are (see [6], [19])

Here

• k : D × [0,T] ® L (³,³) is defined as k_ij(x,t) = d_ijk₁ if x Î K(t), k_ij(x,t) = d_ijk₂ if x Î D\, where k₁, k₂ are the dielectric constants in K(t) and D\ respectively.

• b : D × ® , b(x,y(x,t)) = k₂ sinh y(x,t) if x Î D\, b(x,y(x,t)) = 0 if x Î K(t), is the Debye radius [10].

• Y(x) = , y₁(x,t) = y(x,t)|_K(t) and y₂(x,t) = y(x,t).

• s is a superficial charge distribution and r(x,t) = (r₁(x,t),r₂(x,t)), where

are the charge distribution in K(t) and D\ respectively.

The action of the electrical field on the particle produce its motion. The motion of fluid is described by the velocity field v^f(x,t) (velocity of the fluid material point which has Cartesian coordinates x at time t) and satisfies the Navier-Stokes equation

for all t Î (0,T). Here h > 0 is the viscosity of the fluid, _f > 0 is the homogeneous fluid density (of the mass) and W_T = {(t,x)/t Î (0,T), x Î D\}; denoting r^ions as the ion density of the solution, we have F = -(+r^ions)Ñf₂ as the electrical force on the fluid domain (see [30]). Then F = (r₂+k₂sinh(y₂))(Ñy₂) , using the Boltzmann distribution for r^ions (see [16]).

Let us set x_c(t) as the center of mass of the particle; w(t) the rotation vector; R(t) the translational velocity; A the symmetric inertial matrix; v^p the velocity of the particle. We observe that if _p > 0 is the density (of the mass) of the particle,

for all y Î ³. We have also v^p(x,t) = R(t) + w(t) × (x – x_c(t)) for x Î K(t). It is important to observe the implicit dependence of F on v^p.

From the Newtonian mechanics for rigid bodies and the stress tensor in fluid dynamics, if M is the mass of the particle, the evolution law for the motion is given by

and

If we set D(v^f) = (Ñv^f + (Ñv^f)^T) then s^H(x,t) = 2hD(v^f(x,t)) – p(x,t)I is the stress tensor of the fluid;

is the electrostatic tensor (see [30]).

We assume the following hypotheses on the data

(i) K₀ is a Lipschitz domain.

(ii) D is a C²-domain, Y Î H¹(¶D)ÇC(¶D), s(. ,t) Î L²(¶K(t)), r(. ,t) Î L^¥(D), "t Î [0,T].

Remark 2.1. As remarked in the introduction of this paper, under the above hypotheses we have established elsewhere [6] that

y(. ,t) = (y₁,y₂)(. ,t) Î H¹(D) Ç (H^3/2(K(t)), H^3/2(D\)),

for all t Î [0,T]. This regularity result and Trudinger's inequality (see discussion in [6]) give us that

Recalling the Sobolev embedding H^1/2(D) Ì L³(D), the Hölder's inequality gives us

Then F(. ,t) Î L²(D)³, "t Î [0,T] (evidently this implies F Î L²((0,T) × D)³). A similar calculation shows us that (. ,t) Î L^3/2(D\), "t Î [0,T].

As can be seen in the following section an existence result local in time of the suitable weak solutions for (2.2) coupled with (2.1) is available if we assume that K₀ is a C^1,1-domain.

3 The notion of weak solution

Following [11], let us define the Eulerian densities n_p(x,t) = _pI_K(t)(x),n_f(x,t) = _f(x) and the global density n = n_p+ n_f. We also define the global velocity in D as

In view of the conservation of mass, n satisfies the linear transport equation in D

¶_tn + div(nu) = 0.

We require that v^p · n = v^f · n and s^H · n = T in ¶K(t), where –T is the force applied by the particle on the fluid. We can write T = S · n, where S is the Cauchy stress tensor in the body.

On the walls, we enforce homogeneous Dirichlet boundary conditions u|_¶D = 0. Moreover, the incompressibility of the fluid, the rigidity of the structure and v^p · n = v^f · n imply that div u = 0.

The evolution laws of the momentum for the fluid and for the particle are given by

respectively. Here D(u) = (Ñu + (Ñu)^T) is the global rate-of-deformation tensor.

Introducing the global stress tensor

we obtain the global system in '((0,T) × D)³,

We reproduce here, following the paper [11], the notion of the weak solution of the above system

Definition 3.1. (n,u) is a weak solution of (3.1)-(3.3) in (0,T) if it satisfies the a priori energy bounds

n Î L^¥((0,T) × D), u Î L^¥(0,T; L²(D))³Ç L²(0,T; (D))³,

and if for all fÎ and for almost every t Î (0,T),

where is defined by

= {j Î H¹((0,T) × D)³ / j(t) Î V(t), "t Î (0,T)},

and

V(t) = {j Î (D)³/div j = 0, n_pD(j) = 0}.

The following existence theorem for the above weak solutions is available [11]

Theorem 3.1. Under the hypothesis (ii)-(v) (see Section 4) and the additional assumptions that K₀is a C^1,1-domain,u₀Î (D)³, div u₀ = 0, n_pD(u₀) = 0 and d(0) > d, there exist T* Î (0,+¥] and a solution (n,u) of (3.4) such that

(i) b(n) Î C([0,T]; L^p(W)) Ç L^¥((0,¥) × D) for all T < T*, p < ¥ and b Î C¹(;).

(ii) u Î L^¥(0,T; (D))³and ¶_tu Î L²((0,T) × D)³for all T < T*.

In [11] the hypothesis F Î L²((0,T) × D)³ (a body force) is assumed (see Remark 2.1) and the proof of the existence theorem as Theorem 3.1 is based on the solution of an approximated system (obtained by regularization techniques). The existence of the approximated solutions is obtained by the Schauder fixed-point theorem (see [5]), via a solution of an appropriate inhomogeneous (linear) Stokes equation. Using the C^1,1-regularity of the domains and the smoothness of the coefficients, this linear problem has a solution with the necessary regularity. The solution (u,n) is built as a limit of these approximations; the existence of this limit is derived from the compactness properties of the linear transport equation [12]. This is made possible if we can obtain elliptic estimates and a priori bounds for u as well as energy bounds for n (see Section 4 in [11]). However as F depends on u we need to take some care in this regard. More precisely let us define for each m Î , (u^(m),n^(m),F^(m)) such that n^(m) is bounded in L^¥((0,T) × D) uniformly in m, u^(m) is bounded in L²(0,T;(D) Ç W^1,4(D))³, ¶_tu^(m) is bounded in L²((0,T) × D)³ uniformly in m, converges to n₀ in L²(D), converges to u₀ in L²(D)³ and (3.4) is valid, for all j^(m)Î ^(m). We set K^(m)(t) = M^(m)(t)K₀, where M^(m)(t) is an invertible affine transformation, and we suppose that d = inf{d^(m)(t),t Î [0,T],m > 0} > d, where d^(m)(t) = dist(¶D,¶K^(m)(t)); F^(m) is defined by the calculation of y^(m), the solution of (2.1) considering (K^(m)(t),r^(m),s^(m)). We have to show that < C, where C does not depends on m.

Admitting this uniform bound on F^(m), the stability results [12] for linear transport equation can be used as in [11]: there exist (n,u) such that up to the extraction of a subsequence, b(n^(m)) converges to b(n) weak* in L^¥((0,T) × D) and in C([0,T]; L^p(D)) for all p < +¥ and all b Î C¹(), and u^(m) converges to u in C([0,T]; (D))³ for all s < 1. However, if F is related with y, where y is the solution of (2.1) considering K(t),r,s, it is not obvious that (3.4) holds for (u,n,F) for all given j Î . This is established by the special argument in Section 4 of [11] if we can show that

As we shall see in the next section, in order to establish these results for F^(m),F, we need to study the properties of the solution y of (2.1). Additional hypotheses on r and s are also necessary and as remarked in the Section 2 we shall prove the results in a more general framework: we assume hypothesis (i), i.e., K₀ is a Lipschitz domain.

4 Bounds and convergence for the potentials

As remarked in [6], the determination of the charge densities in bio-molecular systems is a non-trivial question which is treated in some computational studies using Hartree-Fock approximation techniques (see [9], [26]). Here we assume explicitly the following hypothesis

(iii) Let r^(m) as in the Section 3. Then ||r^(m)

< C, where C does not depend on m;

(iv) For all t Î [0,T], s^(m)(M^(m)(t)x,t) = s(M^(m)(t)x ,t) = s(M(t)x,t) = s(x,0), "x Î ¶K₀.

(v) ||r^(m) – r® 0, m ® +¥.

Recalling that Y Î H¹(¶D) and following [6] we consider the problem

which has a solution Î H^3/2(D) such that Î L²(¶K(t)), "t Î [0,T] and

where C depends only on the Lipschitz nature of ¶K₀ (see the papers [8], [31] for details). We observe also that (. ,t) Î L^¥(D) (see [15] or [21]).

Introducing y = + , we see that (2.1) may be reformulated as

Let us consider t Î [0,T] fixed and recall the weak formulation for (4.2).

Find u Î V = (D) such that b(x,u + ) Î L²(D) and satisfying

where

is the usual trace operator. Here k(x,t) = k₁ if x Î K(t), k(x,t) = k₂ if x Î D\.

As can be seen in [6] (see also [19]), this problem is equivalent to find the minimum in (D) of the functional

where J(.) is defined as

Below we establish the first bound on y derived from (4.3)

Lemma 4.1. Let us assume the hypothesis (i)-(iv). Then the solution y Î H¹(D) of (2.1) belongs to L^¥(0,T; H¹(D)) and < M, where M depends only on ||r, ||s(. ,t)||_0,2,¶K(t), k₁, k₂, , D, ¶K₀ and Y.

Proof. By y = + we only need to prove the lemma for . Using (4.3) we have, for all t Î [0,T],

or

where we have used inequalities of Schwarz and Young. Now, recalling that is the minimum of the functional F(.) defined in (4.4), we have F() < F(0) = 0 so that

and

By the trace theorem and Poincaré's inequality there exist constants l₁ = l₁(¶K₀,D) > 0 and l₂ = l₂(D) > 0 such that ||g₀(. ,t)||_0,2,¶K(t)< l₁||(. ,t)||_1,2,D and ||(. ,t)||_1,2,D< l ₂||Ñ(. ,t)||_0,2,D. If we choose 0 < < min(k₁, k₂)/(2), ₁ = ₄ = , ₂ = ₃ = > 0 we have, for C₁ = C₁(k₁, k₂, l₁, l₂), C₂ = C₂(k₁, k₂, l₁, l₂),

Finally, Poincaré's inequality gives us

where

Then

where M = M(C*,Y, ,||s||_0,2,¶K(t)).

The following theorem is central in order to establish an uniform boundfor F^(m).

Theorem 4.1. Let us assume hypotheses (i)-(iv) then the solution y^(m)of (2.1) related with (K^(m)(t),r^(m),s^(m)) satisfies, for each t Î [0,T],

where C does not depends on m.

Proof. We only need to obtain the bounds for . Let us consider the problems

and

Using a variational formulation analogous to that in (4.3) we obtain solutions (weak) v^(m), f^(m)Î (D) of the problems (4.5) and (4.6), respectively. We observe that f^(m) + v^(m) satisfies (2.1) (in the weak sense), from the uniqueness of the variational solution for this problem, we have ^(m) = f^(m) + v^(m).

The Theorem follows from the lemmas below.

Lemma 4.2. Under hypotheses (i)-(iv) the solution v^(m)Î (D) of (4.5) has the additional regularity

for each m> 0 and t Î [0,T]. Furthermore

where C does not depends on m.

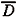Lemma 4.3. Under hypotheses (i)-(iv) the solution f^(m)Î (D) of (4.6) belongs to C⁰() and, for each t Î [0,T],

Furthermore, (. ,t) Î H^3/2(K^(m)(t)), (. ,t) Î H^3/2(D\) and there exists C > 0 such that

where C does not depends on m.

Proof of Lemma 4.2. Let us consider m > 0 and t Î [0,T] fixed and define , then satisfies (in the weak sense)

where µ₂ = and µ₁ = . Following [31], we seek a solution in the form

for z^(m)(. ,t) Î H¹(¶K^(m)(t)), j^(m)(. ,t) Î L²(¶K^(m)(t)) and c^(m)(. ,t) Î H¹(¶D). Here

where G(x) = . The boundary conditions in (4.7) give us (see [6] for details)

where

and

For each m Î and t Î [0,T], the operators

are continuous [8] with operator norms depending only on K₀, D. Observing that

is an equivalent norm to || . ||_1,2,¶D (see [32], Definition 1.9) and using the hypothesis |x – y| > d, "x Î ¶K^(m)(t), "y Î ¶D, a direct calculation gives us that the following trace operators

are bounded and compact, with operator norms depending only on K₀, D and d. The compactness follows from an analogous argument as in [7] (Theorems 1.6, 1.7 and 1.10) if we observe that the kernels are continuous.

Now it follows as in the paper by Torres and Welland [31] that exist and is a bounded operator on X^(m) = H¹(¶K^(m)(t)) × L²(¶K^(m)(t)) × H¹(¶D) to X^(m). The operator norm |||| depends only on d, K₀, D. Then

where X^(m) is equipped with the product norm.

As observed in [31], the operator norms of the operators in (4.9) and its appropriate inverses depend only on the Lipschitz character of the domain, so that there exist L₁ = L₁(¶K₀) > 0, L₂ = L₂(¶D, ¶K₀) > 0, such that, "t Î [0,T],

Hence, using hypothesis (iv), we have established that

where C does not depends on m.

Proof of Lemma 4.3. Let us consider m > 0 and t Î [0,T] fixed. The variational solution f^(m) of (4.6) satisfies

Then the Young's inequality gives us that

Using a similar calculation as in Lemma 4.1, the bound established there for ||

^(m)(. ,t)||_1,2,D and hypothesis (iii), we have ||f^(m)(. ,t)||_1,2,D< C, where C does not depends on m and t. Observing that D is a C²-domain, standard elliptic estimates (see Chapter 14, Theorem 2.1 in [21]) show us that f^(m)(. ,t) Î C⁰(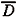). Let us define

In effect, let us suppose that R(t) = +¥, then there exist a subsequence related with , such that (t) ® +¥ with k ® +¥. Let us choose Î 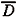such that = (t), then there exists > 0 such that

Recalling that |_¶D = 0, if we take k ® ¥ we have, by the bound ||(. ,t)||_0,2,D< C, ® 0. In this case ||Ñ(. ,t)||_0,2,D® +¥, which contradicts the bound ||(. ,t)||_1,2,D< C.

If we set h^(m) = b(x,f^(m) + v^(m) + + r^(m) we have h^(m)(. ,t) Î L²(D), for all t Î [0,T] and m > 0. Extending h^(m) to be zero outside of D and setting g^(m) = G*h^(m) we have Dg^(m)(. ,t) = h^(m)(. ,t) a.e. in D and g^(m)(. ,t) Î H²(D); if

we have

(see the proof of Theorem B in [20]), while (. ,t) – (. ,t) = 0 a.e. in ¶K^(m)(t). Hence the solution f^(m) of (4.6) can be written as (see [6])

where

and . The operators in ^(m) were defined in (4.9) and ^(m) was defined in Lemma 4.2. The uniform estimate in the H^3/2-norm follows in a similar way as in Lemma 4.2 if we get uniform H^3/2-bounds for g^(m)(. ,t) and H¹-bounds for . From the continuous imbedding H²(D) Ì H^3/2(D) and by the boundedness of the operator F : L²(D) ® H²(D), where Fh^(m)(. ,t) = G*h^(m)(. ,t) = g^(m)(. ,t) (see the proof of Theorem 1 in [32]) we have the bounds

where l depends only on D. A direct calculation and the above estimate give us

where l' = l'(K₀,l), l'' = l''(D,l). Hence we need only obtain an uniform estimate for

We observe that

The result follows using the fact that Y Î L^¥(D), recalling that by Lemma 4.3 we have < +¥ and from the estimate

(see [6] and Lemma 4.2).

Corollary 4.1. < C, where C does not depends on m.

As remarked in the preceding section the solution of (3.4) is constructed as a limit of a sequence of the appropriate approximation solutions and depends on the respective convergence of the force term F^(m) to F in L²((0,T) × D)³. Below we show in detailed manner how to do this. We begin with a technical lemma.

Lemma 4.4. Let us assume hypothesis (i)-(v) and consider y^(m), y the solutions of (2.1) related with (K^(m)(t),r^(m),s^(m)) and (K(t),r,s), respectively. Then, ||y^(m)(. ,t) – y(. ,t)||_1,2,D ® 0, with m ® +¥, for each t Î [0,T].

Proof. Let us set h_m = y^(m) – y. The variational formulation for y,y^(m) gives us

and

If we define A^(m)(t) = K^(m)(t) Ç K(t), B^(m)(t) = D\ we have, after subtracting the above expressions,

Using Young's and Hölder's inequalities and positiveness of the second integral on the right side, we have

Now, following [11],

with m ® +¥, since u^(m) converges to n_pu in C([0,T]; L²(D))³. Hence |K^(m)(t)\A^(m)(t)|, |K(t)\A^(m)(t)| ® 0, m ® +¥. We observe that, by the Theorem 4.1 and the Sobolev imbedding H^1/2(K^(m)(t)) Ì L³(K^(m)(t)),

where C does not depend on m. Similarly, using the Sobolev embedding H¹(D) Ì L⁴(D), Lemma 4.1 and hypothesis (iii) and (iv) we see that uniform bounds to ||h_m||_0,2,D, ||h_m||_0,4,D are available. From hypothesis (v), ||(r^(m) – r)(. ,t)||_0,¥,D® 0. Theorem 4.1 and similar argument as in (4.10) give us that

where C does not depend on m.

Using the rigidness of the particle we have

Now, we introduce, for each m, the usual -regularization {} for h_m such that ||( – h_m)(. ,t)||_1,1,D ® 0 when h ® 0. Observing that

the first integral in (4.12) tends to zero with m ® +¥, as can be seen using the usual trace theorem. Analogously we have the same result for the second integral in (4.12), recalling that , the hypothesis (iv) and regularity (. ,t) Î H^3/2(D).

Theorem 4.2. Let us consider j^(m)Î H¹((0,T) × D)³ such that j^(m)® j strongly in C([0,T];L²(D))³ and j Î H¹((0,T) × D)³. Then

for all t Î (0,T).

Proof. Recalling that F^(m) = , we can write

where C₁ = and C₂ = .

In what follows we shall estimate the integral of each term above.

with m ® +¥. Here we have used the Hölder's inequality, the embeddings H^1/2(D) Ì L³(D) and H^1/2(D) Ì H^3/2(D), Theorem 4.1 jointly with a similar estimate as in (4.10) and the convergence ® 0.

Writing

Ñy sinh(y) – Ñy^(m) sinh(y^(m))

= sinh(y)(Ñy – Ñy^(m)) + Ñy^(m)(sinh(y) – sinh(y^(m)))

we have

Now, observing that if

y^(m) – y > 0, cosh²(y^(m) + q(y – y^(m))) < cosh²(y) and if

y^(m) – y < 0, cosh²(y^(m) + q(y – y^(m))) < cosh²(y – y^(m)),

we have, by Schwarz's inequality

where we have used a similar estimate as in (4.10), Theorem 4.1 and Lemma 4.4. Hence the dominated convergence theorem, Theorem 4.1 and Lemma 4.4 gives us that the terms in (4.15) tends to zero with m ® +¥. Passing the terms in (4.14) to the limit m ® +¥, using (4.11) and Theorem 4.1 we obtain the desired result for the second term in (4.13). The convergence of the others terms in (4.13) to zero follows from a completely similar way, using hypothesis (iii), (iv) and (v), Theorem 4.1 and Lemma 4.4.

Acknowledgment. The first author was supported by a Doctoral Scholarship of the CNPq-Brasil.

Received: 08/IX/04. Accepted: 29/IX/05.

#615/04.

• [1] A. Ajdari, Electro-osmosis on inhomogeneous charged surfaces, Physical Review Letters, 75(4) (1995), 755-758.
• [2] A. Ajdari and D. Long, Symmetry properties of the electrophoretic motion of patterned colloidal particles. Physical Review Letters, 81(7) (1998), 1529-1533.
• [3] S. Allison, C. Cheng and D. Stigter, The Length Dependence of Translational Diffusion, Free solution Electrophoretic Motion and Electrophoretic Tether Force of Rigid Rod-Like Model Duplex DNA. Biophys. J., 81(5) (2001), 2558-2568.
• [4] J.L. Anderson, Colloidal transport by interfacial forces. Ann. Re. Fluid Mech., 21 (1989), 61-99.
• [5] L. Bedin and M. Thompson, Motion of charged particles in ionized fluids via the Poisson-Boltzmann equation. To appear, Math. Models and Methods Appl. Sci
• [6] L. Bedin, M. Thompson and M.T. Vilhena, On the Poisson-Boltzmann equation on non-smooth domains. Int. J. Diff. Eq. App., 8(4) (2003), 327-360.
• [7] D. Colton and R. Kress, Integral Equations Methods in Scattering Theory, John Wiley, New York, (1988).
• [8] M. Costabel, Boundary integral operators on Lipschitz domains: elementary results. SIAM J. Math. Anal., 19 (1985), 613-626.
• [9] L.E. Dardenne, A.S. Werneck, M. Oliveira and P.M. Bisch, Reassociation of Fragments Using Multicentered Multipolar Expansions: Peptide Junction Treatment to Investigate Electrostatic Properties of Proteins. J. Comp. Chem., 22 (2001), 689-701.
• [10] M. Daune, Molecular Biophysics:Structures in Motion. Oxford University Press, Oxford (1999).
• [11] B. Desjardins and M.J. Esteban, Existence of weak solutions for the motion of rigid bodies in a viscous fluid. Arch. Rat. Mech. Anal., 146 (1999), 59-71.
• [12] R.J. DiPerna and P.L. Lions, Ordinary differential equations, transport theory and Sobolev spaces. Inventiones mathematicae, 98(3) (1989), 511-547.
• [13] M.C. Fair and A. Ajdari, Electrophoresis of dumbell-like colloidal particles. Int. J. Multiphase Flow 16(4) (1990), 663-679.
• [14] M. Ferreira, S.L.L. Verardi and J.M. Machado, Electroosmotic Pumping Rectangular Microchannels: a Numerical Treatment by the Finite Element Method. Appl. Math., 2 (2002), 10-15.
• [15] D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order, Springer-Verlag, Berlin, (1977).
• [16] A. Yu. Grosberg and A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, New York, (1994).
• [17] M.D. Gunsburger, H.C. Lee and G.A. Seregin, Global existence of weak solutions for the viscous incompressible flows around a moving rigid body in three dimensions. J. Math. Fluid Mech., 2 (2000), 219-266.
• [18] N.M. Gunther, La Théorie du Potentiel et ses Applications Aux Problčmes Fondamentaux de la Physique Mathématique Gauthier-Villards, Paris, (1934).
• [19] M.J. Holst, The Poisson-Boltzmann Equation: Analysis and multilevel numerical solution (Monograph based on Ph.D.Thesis: Multilevel Methods for the Poisson-Boltzmann Equation). tech. rep., California Institute of Technology, (1994).
• [20] D. Jerison and C.E. Kenig, The inhomogeneous Dirichlet problem in Lipschitz domains. J. Func. Anal., 130 (1995), 161-219.
• [21] O.A. Ladyzhenskaya and N.N. Ural'tseva, Linear and Quasilinear Elliptic Equations Academic Press, New York, (1968).
• [22] V.G. Levich, Physicochemical Hydrodynamics, Prentice Hall, Englewood Cliffs, New Jersey, (1962).
• [23] P. Lions, Mathematical Topics in Fluid Mechanics: Incompressible Models Oxford Interscience, London, (1984).
• [24] D. Long, J.L. Viovy and A. Ajdari, Simultaneous action of electric fields and nonelectric forces on a polyelectrolyte: motion and deformation. Physical Review Letters, 76(20) (1996), 3858-3861.
• [25] C. Miranda, Partial Differential Equations of the Elliptic Type Springer-Verlag, Berlin, (1970).
• [26] H. Nakumura, Roles of eletrostatic interactions in proteins. Quart. J. Biophysics, 29 (1996), 1-90.
• [27] A. Sellier, A note on the electrophoresis of a uniformly charged particle. Q. J. Mech. Appl. Math., 55(4) (2002), 561-572.
• [28] Y. Solomentsev and J.L. Anderson, Electrophoresis of slender particles. J. Fluid Mech., 279 (1994), 197-215.
• [29] T.N. Swaminathan and H.H. Hu, Coiling of a long chain of particles undergoing electrophoresis, Preprint-University of Pennsylvania, (2001).
• [30] M. Teubner, The motion of charged particles in electrical fields. J. Chem. Phys., 76(11) (1982), 5564-5573.
• [31] R.H. Torres and G.V. Welland, The Helmholtz equation and transmission problems with Lipschitz interfaces. Indiana J. Math., 42 (1993), 1457-1486.
• [32] G. Verchota, Layer Potentials and Regularity for the Dirichlet Problem for Laplace's Equation in Lipschitz Domains. J. Func. Anal., 59 (1984), 572-611.

Publication Dates

• Publication in this collection
  28 Sept 2006
• Date of issue
  2006

History

• Received
  08 Sept 2004
• Accepted
  29 Sept 2005