Abstract
In this paper, we improve some boundedness results, which have been obtained with respect to nonlinear differential equations of fifth order without delay, to a certain functional differential equation with constant delay. We give an illustrative example and also verify our main result by means of Liaponov tecnique.
boundedness; Liapunov functional; nonlinear differential equations of fifth
The bounded solutions to nonlinear fifth-order differential equations with delay
Cemil Tunç
Department of Mathematics, Faculty of Arts and Sciences, Yüzüncü Yıl University, 65080, Van-Turkey E-mail: cemtunc@yahoo.com
ABSTRACT
In this paper, we improve some boundedness results, which have been obtained with respect to nonlinear differential equations of fifth order without delay, to a certain functional differential equation with constant delay. We give an illustrative example and also verify our main result by means of Liaponov tecnique.
Mathematical subject classification: 34K20.
Key words: boundedness, Liapunov functional, nonlinear differential equations of fifth.
1 Introduction
Among the scores of articles on the qualitative theory of differential equations, the number of articles on boundedness of solutions to nonlinear fifth order differential equations with delay is significantly less than those on differential equations without delay. For those contributions on the boundedness of solutions of nonlinear fifth order differential equations without delay, one can refer to the papers of Abou-El Ela and Sadek [1], Chukwu [3], Sinha [14], Tunç [15, 16, 17], Yuan Hong [21] and some other references thereof. For those regarding the boundedness of solutions of nonlinear fifth order differential equations with delay, wecite Tunç ([18, 19]). All of the aforementioned contributions have focused onthe Liapunov's second (direct) method [12] utilizing Liapunov functions and functionals.
It is also worth mentioning that the construction of Liapunov functions and functionals for higher order nonlinear differential equations still remains as a general problem. In fact, the construction of Liapunov functional for delay differential equations of higher orders is more difficult than the derivation of Liapunov function for differential equations without delay. Since 1960 many excellent books, most of them in Russian, have been published on the qualitative behaviors of delay differential equations. See, for example, Burton [2], Èl'sgol'ts[4], Èl'sgol'ts and Norkin [5], Gopalsamy [6], Hale [7], Hale and Verduyn Lunel[8], Kolmanovskii and Myshkis [9], Kolmanovskii and Nosov [10], Krasovskii [11], Makay [13] and Yoshizawa [20] and the references listed in these books.
In this paper, we consider nonlinear fifth order delay differential equation
which is equivalent to the system
where 1, 5 and p are continuous functions for the arguments displayed explicitly in equation (1); r is a positive constant , that is, r is a constant delay; α2, α3 and α4 are some positive constants. This fact guarantees the existence of the solution of delay differential equation (1) (see Èl'sgol'ts [4, p. 14]). It is assumed that the derivative  exists and is continuous for all x and all solutions considered are assumed to be real valued. In addition, we assume that the right-hand side of system (2) satisfies a Lipschitz condition in x(t), y(t), z(t), w(t), u(t), x(t - r), y(t - r), z(t - r), w(t - r) and u (t - r). Then the solution is unique (see Èl'sgol'ts [4, p. 15]). Throughout the paper x(t), y(t), z(t), w(t) and u(t) are also abbreviated as x, y, z, w and u, respectively. It should be noted that the equation considered here, (1), is completely different than that investigated by Tunç ([18, 19]).
exists and is continuous for all x and all solutions considered are assumed to be real valued. In addition, we assume that the right-hand side of system (2) satisfies a Lipschitz condition in x(t), y(t), z(t), w(t), u(t), x(t - r), y(t - r), z(t - r), w(t - r) and u (t - r). Then the solution is unique (see Èl'sgol'ts [4, p. 15]). Throughout the paper x(t), y(t), z(t), w(t) and u(t) are also abbreviated as x, y, z, w and u, respectively. It should be noted that the equation considered here, (1), is completely different than that investigated by Tunç ([18, 19]).
2 Preliminaries
In order to reach our main result, we will give some basic information for the general non-autonomous delay differential system, see also Burton [2], Èl'sgol'ts [4], Èl'sgol'ts and Norkin [5], Gopalsamy [6], Hale [7], Hale and Verduyn Lunel [8], Kolmanovskii and Myshkis [9], Kolmanovskii and Nosov [10], Krasovskii [11], Makay [13] and Yoshizawa [20]. Now, we consider the general non-autonomous delay differential system
where : [0, 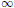 ) × CH
) × CH
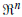 is a continuous mapping, (t, 0) = 0, and we suppose that takes closed bounded sets into bounded sets of
is a continuous mapping, (t, 0) = 0, and we suppose that takes closed bounded sets into bounded sets of 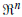 . Here (C,
. Here (C, 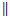 .
.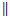 ) is the Banach space of continuous function Φ : [ -r, 0]
) is the Banach space of continuous function Φ : [ -r, 0] 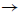
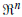 with supremum norm, r > 0; CHis the open H-ball in C;
with supremum norm, r > 0; CHis the open H-ball in C;
 .
.
Standard existence theory, see Burton [2], shows that if Φ  CHand t > 0, then there is at least one continuous solution x(t, t0, Φ) such that on [t0, t0 + α) satisfying equation (3) for t > t0, xt(t, Φ) = Φ and α is a positive constant. If there is a closed subset B
CHand t > 0, then there is at least one continuous solution x(t, t0, Φ) such that on [t0, t0 + α) satisfying equation (3) for t > t0, xt(t, Φ) = Φ and α is a positive constant. If there is a closed subset B  CHsuch that the solution remains in B, then α =
CHsuch that the solution remains in B, then α =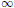 . Further, the symbol |.| will denote the norm in
. Further, the symbol |.| will denote the norm in 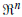 with |x|= max1<i<n |xi|.
with |x|= max1<i<n |xi|.
Definition 1 (See [2]). A continuous function W : [0, 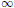 )
) 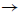 [0,
[0, 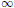 ) with W (0) = 0, W (s) > 0 if s > 0, and W strictly increasing is a wedge. (We denote wedges by W or Wi, where i an integer.)
) with W (0) = 0, W (s) > 0 if s > 0, and W strictly increasing is a wedge. (We denote wedges by W or Wi, where i an integer.)
Definition 2 (See [2]). Let D be an open set in 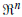 with 0
with 0  D. A function V : [0,
D. A function V : [0, 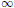 ) × D
) × D 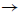 [0,
[0, 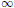 ) is called positive definite if V (t, 0) = 0 and if there is a wedge W1 with V (t, x) > W1(|x|), and is called decrescent if there is a wedge W2 with V (t, x) < W2(|x|).
) is called positive definite if V (t, 0) = 0 and if there is a wedge W1 with V (t, x) > W1(|x|), and is called decrescent if there is a wedge W2 with V (t, x) < W2(|x|).
Definition 3 (See [2]). Let V (t, Φ) be a continuous functional defined for t > 0, Φ  CH. The derivative of V along solutions of (3) will be denoted by
CH. The derivative of V along solutions of (3) will be denoted by  and is defined by the following relation
and is defined by the following relation
where x(t0, Φ) is the solution of (3) with xt0 (t0, Φ) = Φ.
Example. Let us consider the nonlinear second order delay differential equation:
which is equivalent to the system
We assume that the functions  and p are continuous and satisfy the following:
and p are continuous and satisfy the following:
and
for all t, t  [0,
[0, 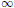 ), x, x(t - r), y and y(t - r), where r is a positive constant, constant delay, which will be determined later; max q(t)<
), x, x(t - r), y and y(t - r), where r is a positive constant, constant delay, which will be determined later; max q(t)< 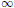 and q
and q
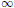 ); is continuously differentiable satisfying the conditions: x-1 (x) > α2,(x
); is continuously differentiable satisfying the conditions: x-1 (x) > α2,(x 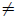 0), and |'(x)| < L for all x; α1,α2 and L are some positive constants. In particular, let us take
0), and |'(x)| < L for all x; α1,α2 and L are some positive constants. In particular, let us take
 .
.
Then, it follows that
 .
.
If we choose
 ,
,
then we have
 ,
,
that is, q
L1(0,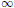 ). Now, we introduce the Liapunov functional
). Now, we introduce the Liapunov functional
 ,
,
where λ is a positive constant which will be determined later. It is clear that the functional V (t, xt , yt) is positive definite:
for all x(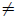 0) and y. Along a trajectory of the equation, we have
0) and y. Along a trajectory of the equation, we have
Hence, we get
In view of afore mentioned assumptions, the inequality 2 |uν|< u2 + ν2 and the fact
we find
If we choose  , then we have
, then we have
 .
.
Therefore, it follows that
for some constant α > 0 provided that r <  . Thus, we get
. Thus, we get
 .
.
Now, integrating this inequality from 0 to t and using the fact  L1(0,
L1(0, 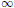 ), we have
), we have
 .
.
Therefore, one can conclude that
for all t > 0. That is,
for all t > 0. This fact shows that all solutions of the equation considered are bounded.
3 Main result
We establish the following result.
Theorem. In addition to the basic assumptions imposed on the functions 1, 5and p appearing in equation (1), we assume that there are positive constants α, α1, α2, α3, α4, ε, ε0, ε1 , δ and λ such that the following conditions hold:
(ii) ε0< 1(t, x(t - r), y(t - r), z(t - r), w(t - r), u(t - r)) - α1< ε1 for all t, x(t - r), y(t - r), z(t - r), w(t - r) and u(t - r), where the constant ε1satisfies the inequality
 .
.
(iii) 5(0) = 0, 5(x) 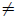 0 if x
0 if x 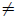 0,x-1 5(x) > α(x
0,x-1 5(x) > α(x 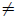 0), and '5(x) < α5 for all x.
0), and '5(x) < α5 for all x.
 .
.
(iv) |p(t, x(t - r), y(t - r), z(t - r), w(t - r), u(t - r))|< q(T) for all t, x(t - r), y(t - r), z(t - r), w(t - r) and u(t - r), where max q(T)< 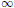 and q
and q
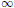 ).
).
Then, there exists a finite positive constant K such that the solution x(t) of equation (1) defined by the initial functions
satisfies the inequalities
for all t >t0, where Φ C4 ([t0 - r, t0], f), provided that
C4 ([t0 - r, t0], f), provided that
 .
.
Proof. For the proof, we introduce the Liapunov functional V0 = V0 (t, xt , yt, zt,wt , ut):
where λ, µ and ρ are some positive constants which will be determined later in the proof and δ is also a positive constant satisfying
Now, in view of (4), it follows that
where
The assumptions 5(0) = 0, 5(x) sgn x > 0, x-1 5(x) > α (x 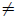 0), '5(x) < α5 and (5) imply that
0), '5(x) < α5 and (5) imply that
and
provided that
 ,
,
which we now assume. Now, the estimates related to V1 and V2 yield
Following a similar way as that of Tunç [18], one can easily conclude from (6) that
for a sufficiently small positive constant D8. Now, let
be a solution of system (2). Then, a direct computation along this solution shows that
In view of the assumptions of theorem and expression (5), we have that
and
By the assumption '5(x) < α5 and inequality 2 |uν|< u2 + ν2, we obtain the following:
and
 .
.
Making use of these inequalities, we get
where
Now, subject to the assumptions (ii) and (iii) of theorem, one easily finds that
V4> 0, V5> 0, V6> 0, V7> 0, V8> 0,
respectively. Gathering the above discussion into (8) and making use of the assumption (ii), it follows that
If we let
then subject to the assumption (i) of theorem the inequality (9) implies that
Thus, one easily obtains that
for some constant τ > 0 provided that
 .
.
Clearly, we have
where
 .
.
Using the fact |y| < 1 + y2, |z| < 1 + z2, |w| < 1 + w2 and |u| < 1 + u2,we see that
 .
.
In view of (7), it follows that
 .
.
Finally, integrating this inequality from t0, (t0> 0), to t and using the assumption q
L1(0,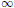 ) and Gronwall-Reid-Bellman inequality, we conclude that
) and Gronwall-Reid-Bellman inequality, we conclude that
where K1 > 0 is a constant,
 ,
,
and
 .
.
Now, the inequality (7) and the last inequality together give that
 ,
,
where K = K1D8-1. This fact completes the proof of theorem. 
Received: 18/IX/08.
Accepted: 09/II/09.
#CAM-23/08.
- [1] A.M.A. Abou-El-Ela and A.I. Sadek, On the boundedness and periodicity of a certain differential equation of fifth order. Z. Anal. Anwendungen, 11(2) (1992), 237-244.
- [2] T.A. Burton, Stability and Periodic Solutions of Ordinary and Functional Differential Equations. Academic Press, Orlando (1985).
- [3] E.N. Chukwu, On the boundedness and stability of solutions of some differential equations of the fifth order. SIAM J. Math. Anal., 7(2) (1976), 176-194.
- [4] L.È. Èl'sgol'ts, Introduction to the theory of differential equations with deviating arguments. Translated from the Russian by Robert J. McLaughlin Holden-Day, Inc., San Francisco,Calif.-London-Amsterdam (1966).
- [5] L.È. Èl'sgol'ts and S.B. Norkin, Introduction to the theory and application of differential equations with deviating arguments. Translated from the Russian by John L. Casti. Mathematics in Science and Engineering, Vol. 105. Academic Press [A Subsidiary of Harcourt Brace Jovanovich, Publishers], New York-London (1973).
- [6] K. Gopalsamy, Stability and oscillations in delay differential equations of population dynamics. Mathematics and its Applications, 74. Kluwer Academic Publishers Group, Dordrecht (1992).
- [7] J. Hale, Theory of Functional Differential Equations. Springer-Verlag, New York-Heidelberg (1977).
- [8] J. Hale and S.M. Verduyn Lunel, Introduction to functional-differential equations. Applied Mathematical Sciences, 99. Springer-Verlag, New York (1993).
- [9] V. Kolmanovskii and A. Myshkis, Introduction to the Theory and Applications of Functional Differential Equations. Kluwer Academic Publishers, Dordrecht (1999).
- [10] V.B. Kolmanovskii and V.R. Nosov, Stability of functional-differential equations. Mathematics in Science and Engineering, 180. Academic Press, Inc. [Harcourt Brace Jovanovich,Publishers], London (1986).
- [11] N.N. Krasovskii, Stability of motion. Applications of Lyapunov's second method to differential systems and equations with delay. Translated by J.L. Brenner Stanford University Press, Stanford, Calif. (1963).
- [12] A.M. Liapunov, Stability of Motion. Academic Press, London (1966).
- [13] G. Makay, On the asymptotic stability of the solutions of functional-differential equations with infinite delay. J. Differential Equations, 108(1) (1994), 139-151.
- [14] A.S.C. Sinha, On stability of a fifth-order nonlinear differential equation. Proceedings of the IEEE, September (1971), 1382-1383.
- [15] C. Tunç, On the boundedness and the stability results for the solutions of certain fifth order differential equations. Istanbul Üniv. Fen Fak. Mat. Derg., 54 (1995), 151-160 (1997).
- [16] C. Tunç, On the boundedness and the stability results for the solution of certain fifth order differential equations. Ann. Differential Equations, 12(3) (1996), 259-266.
- [17] C. Tunç, A study of the stability and boundedness of the solutions of nonlinear differential equations of the fifth order. Indian J. Pure Appl. Math., 33(4) (2002), 519-529.
- [18] C. Tunç, On the boundedness of solutions of nonlinear differential equations of fifth-order with delay. Proceedings of Dynamic Systems and Applications 1, 5 (2008), 466-473.
- [19] C. Tunç, A theorem on the boundedness of solutions to fifth-order nonlinear differential equations with delay. Annales des Sciences Mathématiques du Québec, (2008), (accepted for publication).
- [20] T. Yoshizawa, Stability theory by Liapunov's second method. The Mathematical Society of Japan, Tokyo (1966).
- [21] Y. Yuan Hong, Stability and boundedness of solutions to nonlinear differential equations of the fifth order. (Chinese) J. Central China Normal Univ. Natur. Sci., 24(3) (1990), 267-273.
Publication Dates
-
Publication in this collection
08 July 2009 -
Date of issue
2009
History
-
Received
18 Sept 2008 -
Accepted
09 Feb 2009




 ,
,



































