On a nonstationary nonlinear coupled system

On a nonstationary nonlinear coupled system^*

Gang Li^I; Hui Wang^I; Jiang Zhu^II

^IDepartment of Mathematics, Nanjing University of Information Science & Technology, 210044 Nanjing, China. E-mails: [e-mail] / [e-mail]

^IILaboratório Nacional de Computação Científica, MCT, Avenida Getúlio Vargas, 333, 25651-075 Petrópolis, RJ, Brazil. E-mail: [e-mail]

ABSTRACT

In this paper, a strongly nonlinear coupled elliptic-parabolic system modelling a class of engineering problems with heat effect is studied. Existence of a weak solution is first established by Schauder fixed point theorem, where the coupled functions σ(s), k(s) are assumed to be bounded. The uniqueness of the solution is obtained by applying Meyers' theorem and assuming that σ(s), k(s) are Lipschitz continuous. The regularity of the solution is then analyzed in dimension d < 2 under the assumptions on σ(s), k(s) ∈ C²(R) and the boundedness of their derivatives of second order. Finally, the blow-up phenomena of the system are studied.

Mathematical subject classification: 35J60, 35K55.

Key words: elliptic-parabolic system, existence, uniqueness, regularity, blow-up.

1 Introduction

In many engineering problems, cf. [1, 2, 3], and the references therein, we encounter an incompressible quasi Newtonian flows with viscous heating which can be modelled as:

where u is the velocity, p the pressure, θ the temperature. The viscosity σ is a function of θ,

is the strain rate tensor, and |D(u)|² is the second invariant of D(u).

Problems of this type have received especial attention recently, cf. [2, 4, 5]. Very similar problems can be found in modelling turbulent flows, cf. [6, 7], thermistor problems, cf. [9, 10, 12, 15, 13, 14, 16, 19, 23, 22, 24, 26, 29, 31, 32], semiconductor devices, cf. [30, 17, 28], electromagnetic "induction heating" problems, cf. [11], and so on. The main difficulties in analysis of the system (1) come from the strongly coupled nonlinearity and the incompressibility (from numerical point of view). In this paper, we focus the first difficulty and consider its simplified scalar model:

where u, θ: Ω × (0, T) → are unknowns, Ω is a bounded open subset of ^d, d = 1, 2 or 3, Γ its regular boundary, T is some positive given number. b, c are given vector and scalar functions. We will study the problem (1) in next work.

The model problem (2) can be also thought, from mathematical point of view, as a generalization of thermistor problem where u is potential, θ temperature and f, b, c ≡ 0. It is necessary and important to understand well such a fundamental model problem (2) in simulating quasi Newtonian flows with viscous heating, turbulent flows, thermistor problems, semiconductor devices, electromagnetic "induction heating" problems, etc.

Following the works by Antontsev-Chipot [10] and Elliott-Larsson [16] for thermistor problem, we give in this paper a complete analysis such as existence, uniqueness, regularity and blow-up of the problem (2). While in [24] the authors assumed f ∈ L²( Ω) to get the existence of the solution, we establish similar results with a weaker assumption on it (see Theorem 1 below), which also extends results in [10, 16], where simply f = 0 is involved in the partial differential equation. By applying Meyers' estimate from [21], regularityassumptions on the solution such that

∇u_i, ∇ ϕ₂∈ L^{2q/(q - n)}(0,T; L^q( Ω)), i = 1,2

and

∇ ϕ₁∈ L^{4q/(q - n)}(0,T; L^q( Ω)), q > max(n, 2)

etc. in [10] are not needed to reach the uniqueness of the solution. And a non-trivial extension of the blow-up analysis in [10] to the case of diffusion-convection-reaction is presented following the idea from [8].

The paper is constructed as follows. In section 2 we formulate the variational form of the problem. And the following two sections are devoted to analyze the existence and uniqueness of the weak solution. Then we study the regularity of the solution. Finally, we discuss the blow-up.

2 Variational formulation

We will use standard notation for the spaces and corresponding norms. Let W^m,s( Ω) denotes the standard sobolev space, with its norm , for m > 0 and 1 < s < ∞. We write H^m( Ω) = W^m,s( Ω) when s = 2, with the norm , and L^s( Ω) = W^0,s( Ω) when m = 0, with the norm . ( Ω) is the closure of the space ( Ω) for the norm . When considering space-time functions v(x, t), (x, t) ∈ Ω × (0, T), we define the space L^r(0, T; X)(1 < r < ∞) (where X is a Sobolev space on Ω) as:

In a similar way we can define L ^∞(0, T; X) and C(0, T; X). Vector variables are, in general, denoted with bold face.

We assume that θ₀∈ L²( Ω), and let V = ( Ω), V' = H^-1( Ω) the dual space of V. Then, for a given f ∈ L ^∞(0, T; V'), the variational formulation of the problem (2) can be defined as:

where

and (·, ·) denotes the inner product of [L²( Ω)]^d or the duality between [L^s( Ω)]^d and [L^s'( Ω)]^d, s' is the dual number of s.

3 Existence of a weak solution

We assume that σ, k ∈ C() satisfying

where σ_i, k_i are positive constants. C denotes a generic constant depending on Ω, d and σ_i, k_i.

It is easy to see that, for any given θ, and v, w ∈ V

where is equivalent to the norm ||·||_V by Poincaré inequality (cf. p. 11 in [25]).

To symmetrize the trial and test function spaces of (3.ii), we note that in [24, 32, 33] Meyer's estimate was applied and some regularity assumption in 3D case was needed. Here we are doing in a different way which is based on the Maximum principle and that regularity assumption is then unnecessary.

Lemma 1. For any given θ, the solution to (3.i) u satisfies that

Moreover, if f ∈ L²(0, T;L^q( Ω)) where q > d/2, then

Proof. Let v = u in (3.i), and notice that (7), we can get (9). (10) is a consequence of Theorem 8.16 in [20].

□

By (2.i), the right-hand side of (2.ii) can be written as

Then, for any η ∈ V, we have

By Lemma 1, if f ∈ L ^∞(0, T; V') ∩ L²(0, T; L^q( Ω)), then (12) defines an element of L²(0, T; V'). Thus, we can rewrite (3) equivalently as:

Problem (13) is easier to study since its trial and test function spaces are same.

Since

(b · ∇ θ, θ) = - ( ∇(b θ), θ) = -(b · ∇ θ, θ) - ( ∇ · b θ, θ)

or

So, if

where λ_min denotes the smallest eigenvalue of - Δ in Ω, p > 0 and if

we have, for any ξ, θ, η ∈ V

where α = min(k₁ , p), β = β(k₂, b, c) is a constant.

Then we can prove the following:

Theorem 1. (Existence) If f ∈ L ^∞(0, T; V') ∩ L²(0, T; L^q( Ω)) (q > d/2), and b, c functions satisfying (15), then there exists a weak solution {u, θ} to problem (13) such that

Proof. Choose ξ ∈ L²(0, T; L²( Ω)), since (7), (8) hold, we denote by u _ξ ∈ V the solution of

in view of the Lax-Milgram Theorem.

According the Theorem 2.1 in [10], there exists a unique θ _ξ ∈ L²(0, T; V) ∩C(0, T; L²( Ω)) with ∈ L²(0, T; V') and = θ₀ the solution of

together with k = k( ξ). Let us consider the map

This map carries L²(0, T; L²( Ω)) into itself. Moreover, since (15) holds, by (6) and (17), if choosing η = θ _ξ in (23) and integrating in t, we have

By Hölder, Young's inequalities, the first two terms of the right-hand side of the last equation follows,

Hence, (25) follows

And again, choosing v ∈ L²(0, T; V), = 1 in equation (23), one easily deduce

Therefore, provided we take large enough, ξ → θ _ξ maps the ball B_R of center 0 and radius in L²(0, T; L²( Ω)) into itself. Moreover, since

W = { θ ∈ L²(0, T; V)| θ_t ∈ L²(0, T; V')}

is compactly imbedded in L²(0, T; L²( Ω)), and this mapping will be carried into a relatively compact set by (28), (29). We are then going to show that this map is continuous, it will be done by the Schauder fixed point theorem. We consider a sequence ξ_n ∈ L²(0, T; L²( Ω)) such that

defines as in (22) and = J( ξ_n). We will show that

For that, subtracting the equation satisfied by θ _ξ from the one satisfied by with η = - θ _ξ , we get

By (6), (14), (15) and (17), if integrating in t, we have,

Set

then by Hölder inequality and Poincaré inequality, we get

Thus, taking into account the Definition of I₄, we have

Since is in a relatively compact set of B_R, it is enough to show that θ _ξ is the only limit point for . Let be such limit point, i.e.

= in B_R

provided that we have extracted another sequence of n_m that still denoted by n_m we can assume

Then, since | ∇ θ _ξ|²∈ L¹(Q_T), and by (6), we know almost everywhere by the Lebesgue theorem,

Next, for n = n_m the second integral in the right-hand side of (35) reads

It is clear that

By (36), (6) and Lemma 1, together with the Lebesgue theorem we can obtain III → 0. Next, satisfies

- ∇( σ( ξ_n) ∇ ) = f; = 0 on Γ,

hence

( σ( ξ_n) ∇ , ∇( - u _ξ)) = ( σ( ξ) ∇u _ξ , ∇( - u _ξ))

or

( σ( ξ_n) ∇( - u _ξ), ∇( - u _ξ)) = (( σ( ξ) - σ( ξ_n)) ∇u _ξ, ∇( - u _ξ)),

which implies, for every t,

Thus,

as above for III. By the Poincaré inequality, this implies

and up to an extracted subsequence we can assume

then the Lebesgue convergence theorem gives II → 0, which also implies the third integral in the right-hand side of (35) approaches to zero almost everywhere in Ω × (0, T). Hence → θ _ξ = in L²(0, T; L²( Ω)).

□

4 Uniqueness of the solution

Definition 1. We denote by_s for 1 < s < ∞ the class of regular subsets G in ^d for which the Laplacian operator maps (G) onto W^-1,s(G).

Remark 1. A bounded C¹ domain, for example, is of class _s for every s ∈ (2, ∞), see Theorem 4.6 in [34].

From now on, we assume that Ω is of class

_r* for some r* > 2. For 1 < s < r*, we define M_s > 1 by

It is easy to see that M₂ = 1 and M_s' = M_s.

Lemma 2. ([32]) If r ∈ (2, r*] is such that

then, for any θ, we have

where

Similarly to [24, 32], we have

Lemma 3. Let f ∈ L ^∞(0, T; W^-1,r( Ω)), where r is defined in Lemma 2. Then, for any given θ, the solution to (13.i) u ∈ L ^∞(0, T; ( Ω)) and satisfies that

where γ is defined by (43).

Lemma 4. Under the assumptions of Lemma 3, if b, c are bounded continuous functions, σ, k ∈ L ^∞(), then solution to (13.ii) θ ∈ W^r with θ(0) = θ₀, where

W^r = { θ ∈ L^r(0, T; W^1,r( Ω)) : θ_t ∈ L^r(0, T; W^-1,r( Ω))}.

Proof. Since u ∈ L ^∞(0, T; W^1,r( Ω)), it follows that σ( θ)| ∇u|²∈ L ^∞(0, T; L^r/2( Ω)) L ^∞(0, T; W^-1,r( Ω)) L^r(0,T; W^-1,r( Ω)). Following the idea of Theorem 1 and Remark 5 in [21], and the similar proof in Chapter 4 of [18] we can complete the proof.

□

To study the uniqueness of problem (13), we need to assume that: σ, k are Lipschitz continuous, i.e. there is a Lipschitz constant L, for any ξ₁, ξ₂∈ such that,

Let (u_i, θ_i), i = 1, 2, two weak solutions to problem (13), and set = θ₁- θ₂, = u₁ - u₂, noticing (4), we have ∀ v ∈ V,

a( θ₁; , v) = a( θ₁; u₁, v) - a( θ₁; u₂, v) = a( θ₂; u₂, v) - a( θ₁; u₂, v).

Therefore, letting v = , by (7) and (45), we have

or

On the other hand, subtracting the equation satisfied by θ₁ from the one satisfied by θ₂, we get, for any η ∈ V,

Let η = , and noticing (17), we have

By Hölder and Young inequalities, we easily can deduce that

Combining the above estimates and (46), choosing ε = , (47) follows

By the Galiardo-Nirenberg interpolation inequality, (48) becomes

where we apply Young's inequality ab < εa^r/d + C _εb^{r/(r - d)} . Again choosing ε = , and by the estimates in Lemma 3, 4, and by Sobolev inequality that L^r(0, T) ⊂ L^{2r/(r - d)}(0, T), Gronwall lemma implies that

Thus, by (46), uniqueness of the solution follows. Therefore, with the above result, we can state:

Theorem 2. (Uniqueness) Under the conditions of Lemmas 3 and 4 with Lipschitz assumption on k, σ as (45), there exists at most one weak solution to problem (2).

Remark 2. Here the uniqueness result is obtained without additional regularity assumptions on the solution as those required in [10].

5 Regularity of the solution

In this section we study the regularity of the solution to the problem (2) only on the dimension of space d < 2( in [33] we considered a simplified case of k( θ) ≡ 1). For our regularity estimates, we need to assume that

for all s ∈ , where L' is some positive constant.

Then we have:

Theorem 3. (Regularity) Let T > 0 and assume that θ₀∈ H²( Ω) ∩ ( Ω), b,c are bounded continuous functions. f ∈ C²(0, T; L^r( Ω)) where r is defined in Lemma 2. Then problem (2) has a unique solution u ∈ L ^∞(0, T; H²( Ω)), θ ∈ C¹(0, T; L²( Ω)) ∩ C(0, T; H²( Ω)). Moreover, there is a constant C, depending on T, θ₀, f, Ω and on σ, k through the constants σ_i, k_i in (6), such that for every t ∈ [0, T], we have

Proof. We consider the initial value problem ( here V = H²( Ω) ∩( Ω))

where u(t) is determined by the linear elliptic problem

we are now to analyze the regularity of the solution.

Step 1. We first show some estimates of u. By (10), we know

for some q > d/2. Next, by Lemma 3, there existes a 2 < r < r* such that . This implies that for every t,

We note that we should consider mostly the derivatives of σ( θ) to obtain further estimates of u. First, equation (51) implies that - σ( θ) Δu - ∇ σ( θ)· ∇u = f, so that by Hölder inequality,

for any r₁, r₂ satisfying . We thus obtain

Hence, by Gagliardo-Nirenberg interpolation inequality and estimate (53), we will get

where δ = 1 - d/r + d/r₂ = 1-d/r₁. In the last step we also used Young's inequality

ab< ε^1-1/δa^1/δ + εb^1/(1-δ), ε > 0, 0 < δ < 1, a, b > 0

For the above estimates of to hold, it is required that r₁ < ∞, which in its turn is equivalent to δ < 1. Thus, we have proved the preliminary estimate

where C is independent of δ. Next, arguing as [16] treats, we get

where ρ < 1 if d < 2.

Step 2. We now estimates and . First, without lost of generality, we assume that < C (see Lemma 4). We note that it suffices to estimate . In fact, equation (50) implies that θ_t - k( θ) Δ θ + b · ∇ θ + c θ = P( σ( θ)| ∇u|² + k'( θ)| ∇ θ|²), where P denotes the orthogonal projection onto V. Hence,

By the interpolation inequality, we know the two terms in the last inequality can be estimaed by , and in view of the estimate (55), so we can get

For the further estimates of θ_t, we differentiate equations (50) and (51) with respect to t. Beginning with (51), we have

Because σ( θ) is continuous in C(), and in view of (55), we have

Next, by (12), if differentiating equation (50), we have

for each η ∈ V, where (k( θ) ∇ θ)_t = k'( θ) θ_t ∇ θ + k( θ) ∇ θ_t. Similarly, ifcondition (15) is satisfied, with η = θ_t in above equation, we would get

where

1/r + 1/ = 1/2. By Sobolev's inequality and known bounds for u and u_t in (52), (53), (55), (58), we get , thus (60) follows

Since θ(0) = P( θ₀), thus

then by (55),

Therefore, integrating (61) in t, we get

By Gronwall's lemma, we obtain

We are now to establish the estimates of the right hand side of the above inequality. Taking η = θ_t in (50),

In view of (56) and Sobolev inbedding inequality, if integrating in t, we arrive at

since θ(0) = P( θ₀), where P is bounded with respect to the norm , which implies (62) is bounded by C.

Substituting this result into (54), (55), (56), (58), we may conclude that

Step 3. We next to estimate and . We note that θ_tt - ∇·(k( θ) ∇ θ)_t + b· ∇ θ_t + c θ_t = P( σ( θ)| ∇u|²)_t , where

∇(k( θ) ∇ θ)_t = k"( θ) θ_t| ∇ θ|² + 2k'( θ) ∇ θ_t∇ θ + k'( θ) θ_tΔ θ + k( θ) Δ θ_t

and

so it is easy to get the following estimates by (65),

In order to obtain estimate of , we differentiate (50) with respect to t and let η = θ_tt, similar disposal like before, and in view of (66) and (67), we get

Hence, if multiplying by t and integrating in t, it follows

by virtue of (62) and (64). We then differentiate (59) with respect to t and let η = θ_tt to have

where

we could use similar method as above to treat them separately, then, if condition (15) is satisfied, we obtain

Differentiating (57) with respect to t, we have

( σ( θ) ∇u_tt, ∇v) + ( σ( θ)_tt∇u + 2 σ( θ)_t∇u_t, ∇v) = (f_tt, v) ∀v ∈

with v = u_tt, it follows

For the term

( σ( θ)u ∇u)_tt = σ( θ)_ttu ∇u + σ( θ)u_tt ∇u

+ σ( θ)_ttu ∇u_tt + 2 σ( θ)_tu_t∇u + 2 σ( θ)_tu ∇u_t + 2 σ( θ)u_t∇u_t

we estimate similarly to [16] to get , together with (70) show (69) could be estimated by

If we multiply by t² and integrate, and in view of (68), it follows

which completes the proof.

□

6 Blow-up result

In this section we are interested to investigate under what condition the solution exists globally or finite time blow-up? We consider the problem as follows:

where ∂/ ∂ ν is the outward normal derivative of ∂ Ω.

We note that our difficulty to treat problem (71) compared to generalconsidered problem lies in the convection term b · ∇ θ and reaction term cθ. From the physical point of view in [8], any solution θ to (71) can be writtenas θ(x, t) = (x - tb,t), by a variable transformation, we can obtain theequations that 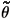and corresponding solution 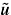satisfy,

where we still write x, t if not causing any confusion and Ω_t = Ω - tb. We note that this transformation does not change the shape of the boundary Γ of Ω and initial value θ₀. In this case we see that if 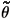blow up so does θ and vise versa, thus the convection term has no effect on whether solution is blow-up in finite time. So we turn our attention to problem (72). We assume that

and

From [10], if d γ(x) is the superficial measure on Γ, then

achieves its minimum value for

thus, if we set

udx, we have for some constant C,

so we get

where C denotes the best constant. Then we have the following result:

Theorem 4. Assume that c is nonpositive function and

where

then problem (71) cannot have a smooth global solution.

Proof. The proof is similar to that of Theorem 5.1 in [10].

□

Remark 3. In one dimension case, when k ≡ 1 and b is a function of x with ∇ b + c > 0, we could show that θ(x, t) blow up globally. In other words, if t* denotes the blowup time when

θ(x, t) → ∞, a.e. x ∈ Ω when t → t*

Indeed, consider Ω = (0,1), then integrate the equation

( σ( θ)u')' = f

it follows

thus the equation satisfied by θ reads

Differentiating in x and let η = θ_x, we see that

with initial boundary

η(x, t) = 0, x = 0,1 η(x, 0) = ( θ₀)_x

Assuming that ( θ₀)_x∈ L ^∞(0,1), and noting that

then it follows from the parabolic maximum principle that

| θ_x| _∞ < |( θ₀)_x| _∞

i.e.

shows that if θ(x₀, t) blows up, then θ blows up for any x.

Remark 4. We note that the result of Theorem 4 is independent of f, then, without loss of generality, we specialize the problem (72) in one dimension with f = 0 to show the sharpness of (76). Still consider Ω = (0,1), 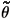(0) = θ₀ = Const and look for a solution 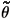= 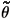(t) depending on t only. Set

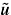₀(-tb, t) = a₀(t), ₀(1 - tb, t) = a₁(t)

then the equation satisfied by u leads to

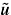(x, t) = a₀(t) + x(a₁(t) - a₀(t))

thus, the equation satisfied by θ becomes

_t - c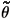 = σ(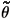)a₁(t) - a₀(t))²

i.e.

or

In this case, the failure of (76) reads

which implies that (72) has a global solution which is bounded when

and is unbounded otherwise.

Acknowledgements. The authors would like to thank Professor Hongwei Wu from Southeast University, Mr. Zhifen Xu and Miss Danni Hu from Nanjing University of Information Science & Technology for their helpful suggestions and discussions.

Received: 18/VI/10.

Accepted: 18/IX/10.

#CAM-225/10.

• [1] P. Avenas, J.F. Agassant and J.Ph. Sergent, La mise en forme des matières plastiques Lavoisier (1982).
• [2] J. Baranger and A. Mikelić, Stationary solutions to a quasi-Newtonian flow with viscous heating Math. Models Methods Appl. Sci., 5 (1995), 725-738.
• [3] J. Bass, Thermoelasticity McGraw-Hill Encyclopedia of Physics, S.P. Parker ed., McGraw-Hill, New York (1982).
• [4] S. Wardi, A convergence result for an iterative method for the equations of a stationary quasi-newtonian flow with temperature dependent viscosity M2AN: Modél. Math. Anal. Numér., 32 (1998), 391-404.
• [5] J. Zhu, A.F.D. Loula, J. Karam F. and J.N.C Guerreiro, Finite element analysis of a coupled thermally dependent viscosity flow problem Comput. Appl. Math., 26 (2007), 45-66.
• [6] R. Lewandowski, Analyse Mathématique et Océanographie Masson (1997).
• [7] B. Mohammadi and O. Pironneau, Analysis of the k-Epsilon model Masson, (1994).
• [8] J. Aguirre and M. Escobedo, On the blow-up of solutions of a convective reaction diffusion equation Proceedings of Royal Society of Edinburgh, 123A (1993),433-460.
• [9] W. Allegretto and H. Xie, Solutions for microsensor thermistor equations in the small bias case. Proc. Roy. Soc. Edingburgh Ser. A, 123 (1993), 987-999.
• [10] S.N. Antontsev and M. Chipot, The thermistor problem: existence, smoothness, uniqueness, blowup SIAM, J. Math. Anal., 25 (1992), 1128-1156.
• [11] A. Bossavit and J.-F. Rodrigues, On the electromagnetic "induction heating" problem in bounded domains Adv. Math. Sci. Appl., 4 (1994), 79-92.
• [12] X. Chen and A. Friedman, A free boundary problem for a nonlinear degenerate elliptic system modeling a thermistor. Ann. Scuola Norm. Sup. Pisa Cl. Sci., 19 (1992), 615-636.
• [13] G. Cimatti, A bound for the temperature in the thermistor problem IMA J. Appl. Math., 40 (1988), 15-22.
• [14] G. Cimatti and G. Prodi, Existence results for a nonlinear elliptic system modelling a temperature dependent electrical resistor Ann. Mat. Pura Appl., 152 (1989), 227-236.
• [15] S. Clain, J. Rappaz, M. Swierkosz and R. Touzani, Numerical modelling ofinduction heating for two-dimensional geometries Math. Models MethodsAppl. Sci., 3 (1993), 805-822.
• [16] C.M. Elliott and S. Larsson, A finite element model for the time-dependent Joule heating problem Math. Comp., 64 (1995), 1433-1453.
• [17] J. Fan and H. Wu, On the N-dimensional stationary drift-diffusion semiconductor equations Nonlinear Anal., 43 (2001), 127-135.
• [18] A. Friedman, Partial Differential Equations of Parabolic Type Englewood Cliffs, N.J., Prentice-Hall (1964).
• [19] T. Gallouët and R. Herbin, Existence of a solution to a coupled elliptic system Appl. Math. Lett., 7 (1994), 49-55.
• [20] D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order, second edition, Springer-Verlag, Berlin (1983).
• [21] K. Gröger, W^1,p-estimates of solutions to evoluton equations corresponding to nonsmooth second order elliptic differential operators Nonlinear Anal. Theory, Meth. & Appl., 18 (1992), 569-577.
• [22] P. Guan, Existence, boundedness and uniqueness of weak solution for thethermistor problem with mixed boundary conditions Acta Mathematica Scientia, 18 (1998), 326-332.
• [23] H.D. Howison and J.F. Rodrigues and M. Shillor, Stationary solutions to the thermistor problem. J. Math. Anal. Appl., 174 (1993), 573-588.
• [24] A.F.D. Loula and J. Zhu, Finite element analysis of a coupled nonlinear system Comput. Appl. Math., 20 (2001), 321-339.
• [25] A. Quarteroni and A. Valli, Numerical Approximation of Partial Differential Equations Springer Series in Computational Mathematics, Vol. 23, Springer-Verlag (1997).
• [26] P. Shi, M. Shillor and X. Xu, Existence of a solution to the Stefan problem with Joule's heating J. Differential Eq., 105 (1993), 239-263.
• [27] Y. Wang, Nonlinear Partial Differential Equations Southeast University Press, (1992).
• [28] J. Xing and Y. Wang, The initial boundary value problem of semiconductor equations wiht heat conduction. Acta Math. Appl. Sinica (in Chinese), 21 (1998), 215-223.
• [29] X. Xu, On the existence of bounded temperature in the thermistor problem with degeneracy Nonlinear Anal., 42 (2000), 199-213.
• [30] H.M. Yin, The semiconductor systems with temperature effect J. Math. Anal.Appl., 196 (1995), 135-152.
• [31] G. Yuan and Z. Liu, Existence and uniqueness of the C ^α-solution for thethermistor problem with mixed boundary values SIAM J. Math. Anal., 25 (1994), 1157-1166.
• [32] J. Zhu and A.F.D. Loula, Mixed finite element analysis of a thermally nonlinear coupled problem Numer. Methods Partial Differential Eq., 22 (2006), 180-196.
• [33] H. Wang, G. Li, J. Zhu and D. Hu, Existence and regularity of solution to a thermally coupled nonstationary sysytem Chin. Quart. J. of Math., 23(4) (2008), 512-524.
• [34] C.G. Simader, On Dirichlet's Boundary Value Problem Lecture Notes in Mathematics 268, Springer-verlag, Berlin (1972).

*

This work was supported partially by the National Natural Science Foundation of China (40537034) and the Brazilian National Council for Scientific and Technological Development (CNPq).

Publication Dates

• Publication in this collection
  06 Jan 2012
• Date of issue
  2011

History

• Accepted
  18 Sept 2010
• Received
  18 June 2010