Abstract
In this work, a consistent stabilized mixed finite element formulation for incompressible pseudoplastic fluid flows governed by the Sisko constitutive equation is mathematically analysed. This formulation is constructed by adding least-squares of the governing equations and of the incompressibility constraint, with discontinuous pressure approximations, allowing the use of same order interpolations for the velocity and the pressure. Numerical results are presented to confirm the mathematical stability analysis. Mathematical subject classification: Primary: 65M60; Secondary: 65N30.
finite element method; numerical analysis; Sisko relation; non-Newtonian flow
A stabilized finite element method to pseudoplastic flow governed by the Sisko relation
Marcio Antônio BortolotiI; José Karam FilhoII, * * Corresponding author
IDepartamento de Ciências Exatas, Universidade Estadual do Sudoeste da Bahia, UESB, Estrada do Bem-Querer, Km 4, 45083-900 Vitória da Conquista, BA, Brazil E-mail: marciob@lncc.br
IICoordenação de Mecânica Computacional, Laboratório Nacional de Computação Científica, LNCC, Av. Getúlio Vargas, 333, 25651-070 Petrópolis, RJ, Brazil E-mail: jkfi@lncc.br
ABSTRACT
In this work, a consistent stabilized mixed finite element formulation for incompressible pseudoplastic fluid flows governed by the Sisko constitutive equation is mathematically analysed. This formulation is constructed by adding least-squares of the governing equations and of the incompressibility constraint, with discontinuous pressure approximations, allowing the use of same order interpolations for the velocity and the pressure. Numerical results are presented to confirm the mathematical stability analysis.
Mathematical subject classification: Primary: 65M60; Secondary: 65N30.
Key words: finite element method, numerical analysis, Sisko relation, non-Newtonian flow.
1 Introduction
In modeling some kinds of fluids, the Sisko constitutive relation comes out from the Cross model [6], when the apparent viscosity lies in a range between the pseudoplastic region and the lower Newtonian plateau. A good alternative constitutive equation of the Sisko type for blood flow has been proposed by [13], for example.
The nonlinearity of this relation together with the incompressibility constraint may generate numerical instabilities when some classical numerical methods are used. For classical methods, in case of velocity and pressure formulations, it is well known that, even for the linear case, different interpolation orders for these variables have to be used in order to satisfy the Babuka-Brezzi stability condition [2, 4].
In this work, to avoid the use of penalization methods or reduced integrationand to recover the stability and accuracy of the solution of same interpolation orders in primitive variables, a consistent mixed stabilized finite element formulation is presented. It is constructed by adding the least-squares of the governing equations and the incompressibility constraint, with continuous velocity and discontinuous pressure interpolations. The present formulation is here mathematically analysed based on Scheurer's theorem, [12]. Stability conditions and error estimates are established when the Sisko relation is considered. Numerical examples are presented to confirm the stability analysis.
2 Definition of the problem
Let Ω be a bounded domain in
n where the positive integer n, denotes the space dimension. We consider the stationary incompressible creep flow problem governed by - div σ = f in Ω, where σ : Ω →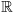 n×
n× 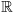 n denotes the Cauchy stress tensor for the fluid and f denotes the body forces.
n denotes the Cauchy stress tensor for the fluid and f denotes the body forces.
The governing equation, written above, is subjected to the incompressibility constraint div u = 0 in Ω, where u denotes the velocity field.
The Sisko model is characterized by a linear supersposition between theNewtonian and the pseudoplastic effects, presenting a dependence of the viscosity µ with the shear-strain rate tensor, defining an apparent viscosity µ(|ε(u)|), leading to the stress tensor of the form
σ = -pI + µ(|ε(u)|)ε(u) with µ(|ε(u)|) = λ1 + λ2ν(|ε(u)|)
and ν(s) = sα - 2, where λ1, λ2 are two positive constitutive constants, α ∈ ]1,2[ is the power index, p is the hydrostatic pressure, I ∈ 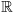 n ×
n × 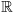 n is the identity tensor, | · | denotes the Euclidean tensor norm and
n is the identity tensor, | · | denotes the Euclidean tensor norm and
is the symmetric part of the gradient of u.
With the above considerations, together with boundary condition of Dirichlet type, the resulting problem is: find (u, p) ∈ C2(Ω) × C1(Ω) such that
where ∂Ω denotes the boundary of Ω.
Physically, pseudoplastic flows are characterized by a viscosity decreasing continuously and smoothly with increasing of shear rate, and this behaviour occurs in a limited range of shear rate, generating the viscosity plateaus, where we can see that the apparent viscosity µ(s) is a bounded continuous function such that
for 0 < g0< s < g∞ with g0 and g∞ being the shear rate finite limits and µ0 and µ∞ corresponding to the finite limiting Newtonian plateaus for low and high shear rate, respectively, [3].
It can be seen that from continuous classical Galerkin formulation associated with problem (1), we can obtain
for all u ∈.jpg" width="35" height="25" align="absmiddle">(Ω), where C is the constant in Poincaré's inequality.
3 Petrov-Galerkin-Like formulation
To generate the stabilized finite element method proposed here, the following definitions will be used.
Let Lp(Ω) = {u|u ismeasurable, ∫Ω|u(x)|p dΩ < ∞} be the class of all measurable functions u, such that, u is p-integrable in Ω and let  (Ω) = {u ∈ Lp(Ω), ∫Ωu dΩ = 0} be the class of functions in Lp(Ω) such that u has null mean. Let Wm,p(Ω) be the Sobolev space Wm,p(Ω) = {u ∈ Lp(Ω)|Dβu ∈ Lp(Ω), 0 < |β| < m} with
(Ω) = {u ∈ Lp(Ω), ∫Ωu dΩ = 0} be the class of functions in Lp(Ω) such that u has null mean. Let Wm,p(Ω) be the Sobolev space Wm,p(Ω) = {u ∈ Lp(Ω)|Dβu ∈ Lp(Ω), 0 < |β| < m} with
where βi is a natural integer and |β| = β1 + ... + βm. The  (Ω) is defined as the space of functions u ∈ Wm,p(Ω) such that Dβu = 0 on ∂Ω, for all β with |β| < m - 1, [1].
(Ω) is defined as the space of functions u ∈ Wm,p(Ω) such that Dβu = 0 on ∂Ω, for all β with |β| < m - 1, [1].
The norm in the space Wm,p(Ω) is defined as
where ||u||p is the Lp(Ω) norm defined as
In this paper, we will denote ||u||1 = ||u||1,2 and ||u||0 = ||u||2.
We assume for simplicity Ω ⊂
n, a polygonal domain discretized by aclassical uniform mesh of finite elements with Ne elements, such that
where Ωe denotes the interior of the eth element and  is its closure.
is its closure.
Let  (Ω) be the finite element space of the Lagrangean continuous polynomials in Ω of degree k and
(Ω) be the finite element space of the Lagrangean continuous polynomials in Ω of degree k and  (Ω) the finite element space of the Lagrangean discontinuous polynomials in Ω of degree l. Thus we can define the approximation spaces Vh = (
(Ω) the finite element space of the Lagrangean discontinuous polynomials in Ω of degree l. Thus we can define the approximation spaces Vh = ( (Ω) ∩
(Ω) ∩  (Ω))n and Wh =
(Ω))n and Wh =  (Ω) ∩ L2(Ω) to velocity and pressure respectively, that can be generated by triangles or quadrilaterals.
(Ω) ∩ L2(Ω) to velocity and pressure respectively, that can be generated by triangles or quadrilaterals.
Remark 3.1. For the Galerkin method, k and l must be different orders even for k > 2 and one can follow [7, 8] and [9], for example, to see the limitations for the combinations of k and l.
Remark 3.2. With the present consistent stabilized formulation, all the combinations of different orders are possible, optimal and suboptimal, but it is possible to use same orders for k and l, with complete polynomials, providing k > 2, as follows.
In this work, to obtain velocity and pressure approximations to problem (1), we define the following variational form, constructed by adding the least squares of the linear momentum and of the continuity equations to the Galekin formulation, generating the following problem with homogeneous boundary condition considered without lost of generalities:
Problem PGhd. Given f ∈ W-1,2(Ω), the dual of W1,2(Ω), find Uh ∈ Vh × Wh, such that
where
with h denoting the mesh parameter, µ(|ε(uh)|) the apparent viscosity,
δ1 and δ2 being positive constants denoted as stability parameters, Δµ uh = div (µ(|ε(uh)|)ε(uh)), Uh = {uh, ph}, Vh = {vh, qh} and ϑ being a dimensional parameter. We can note that when δ1 = δ2 = 0, Problem PGhd reduces to the Galerkin formulation which, for interpolations of same order, is unstable exhibiting spurious pressure modes or presenting the locking of the velocity field, [9]. The nonlinear Problem PGhd preserves the good properties of the linear analogous of [11] in the sense that it accommodates, for k > 2 equal-order interpolations for velocity and pressure as will be shown in the followinganalysis and confirmed later by the obtained numerical results.
This formulation is consistent, being easy to verify that the exact solution of problem defined in (1), U = {u, p}, satisfies the PGhd problem.
4 Finite element analysis
The finite element analysis is developed here by considering solutions in Hilbert Spaces, as in [10]. We start the analysis by rewriting the discontinuous pressure approximation ph as
with 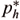 ∈
∈  and
and 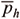 ∈
∈  where
where  is the subspace of the pressure with zero mean at the element level and
is the subspace of the pressure with zero mean at the element level and  is the subspace of the piecewise constant pressure, where
is the subspace of the piecewise constant pressure, where  represents the constraint of ph inelement Ωe.
represents the constraint of ph inelement Ωe.
The discontinuous pressure allows the satisfaction of the incompressibility constraint at element level in contrast to the continuous approximations, which satisfies the constraint only in global sense. Considering this segregation, the Problem PGhd can be rewritten as the following variational form, which considers the pressure variable ph written as functions of 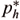 ∈
∈  (Ω) and
(Ω) and 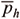 ∈
∈  , as was described above:
, as was described above:
Problem
. Given f ∈ W-1,2(Ω), find {uh,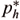 ,
, 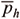 } ∈ Vh ×
} ∈ Vh ×  ×
×  , such that
, such that
where
 and
and  .
.
Lemma 4.1. For µ(s) bounded, continuous and smooth real function such that |dµ(s)/ds| < M, there exists a positive constant C, independent of h, such that h||Δµuh||0h < C||ε(uh)||0where
= (u, u)h.Proof. From the inverse estimate
typical of finite element methods, [5], 0 < µ∞ < µ(s) < µ0 and |dµ(s)/ds| < M, we have the inverse estimate proposed, with C = µ0Ch + M.
□
Lemma 4.2. Assuming the same considerations of Lemma 4.1, there is a positive constant Cl, independent of h, such that, h|| - Δµuh + Δµvh||0h< Cl||ε(uh) - ε(vh)||0 for all uh, vh∈ Vh with h > 0.
Proof. From the triangular inequality, the Lemma 4.1 and (12) we have
The mean value theorem yields
Since |dµ(s)/ds| < M for all uh∈ Vh and from Korn's inequality, we can conclude the result, with the constant Cl given by
where CK is the constant of the Korn's inequality. The lemma is obtained as a consequence of
that is, naturally, obtained from Problem PGhd and consequently yields Cl as a finite constant, where C is the constant of the Poincaré inequality.
□
Definition 4.3. Let || |Uh| || = ||Uh|| + h(|| div ε(uh)||0h + ||ε(uh)||0h + ||∇ph||0h) be a mesh-dependent norm on the product space  (Ω) × L2(Ω), where h denotes the mesh parameter and ||Uh||2 =
(Ω) × L2(Ω), where h denotes the mesh parameter and ||Uh||2 =  is the norm defined in Vh × Wh.
is the norm defined in Vh × Wh.
Lemma 4.4 (Equivalence of the norms). There exists a positive constant κ such that ||Uh|| < || |Uh| || < κ||Uh|| for all Uh∈ Vh.
Proof. The inequality ||Uh|| < || |Uh| || is immediate. In other hand, from the definition of || |Uh| ||, from the inverse estimate (12) and from the inverse estimate for the pressure, see [5],
we have || |Uh| || < ||Uh|| + (Ch + 1)||ε(uh)||0 + Cp||ph||0. Using the classical inequality,
we complete the proof of Lemma 4.4, with κ = 1 + max{Ch + 1, Cp}.
□
With the above results we can establish the following result that will be needed later to generate the estimates in Theorem 4.9.
Theorem 4.5. There exists a positive constant γc such that
for all U* ∈  (Ω) × L2(Ω) and
(Ω) × L2(Ω) and  .
.
Proof. By the consistency of the problem  and from (4) we have
and from (4) we have
From the continuity of the two first terms in the right hand side above, [12], and using the inequality (14) we have
By using Lemma 4.2 and identifying the || | · | || norm, we can conclude
where γc = max{ λ1 + λ2 + n ϑδ2,  ,
,  }.
}.
□
Theorem 4.6. Let Kh = {vh∈ Vh, Bh( , vh) = 0, for all
, vh) = 0, for all  ∈
∈  }. Then, there exists a positive constant γe such that
}. Then, there exists a positive constant γe such that
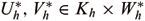 .
.
Proof. From (8) we obtain
From the ellipticity of the last term in the right hand side above, presented in [12], and using the Young inequality with ξ =  we have
we have
Applying again the Young inequality it yields
with η > 0. From Lemma 4.2 and considering r1 and r2 as two positive constants, such that  = 1, we can rewrite the previous inequality as
= 1, we can rewrite the previous inequality as
Choosing η =  , we obtain
, we obtain
By using the inequality
as in [10], and the Korn's inequality, we have
with
since
□
The inequality (16) gives a sufficient condition, providing a useful relation to be used to choose the stabilizing parameters.
Theorem 4.7. There exists a positive constant γB such that
for all  ∈ L2(Ω),
∈ L2(Ω),  ∈ Vh ×
∈ Vh ×  .
.
Proof. This result comes from the application of the Hölder-Schwarz inequality and by the use of (14).
□
Theorem 4.8. For k > 2 and since ['V]h∈ Vh ×  , there exists a positive constant βh, independent of h, such that
, there exists a positive constant βh, independent of h, such that
Proof. This result may be seen in [7].
□
With the above results, we can establish the following error approximation estimates.
Theorem 4.9. There exists a positive constant ζh, independent of h, such that the following estimate holds || |U - Uh| || < ζh|| |U - Vh| ||.
Proof. From the definition of ( (·),·) and the consistency of the formulation we can write
(·),·) and the consistency of the formulation we can write
with
Replacing (18) in (17) we have
From Theorem 4.5, Theorem 4.6, Theorem 4.7 and considering the norm equivalence between || | · | || and || · || established in Lemma 4.4, we have
In order to obtain an estimate to || -
-  h||0, we note that from PGhd problem, we have
h||0, we note that from PGhd problem, we have
Since vh∈ Kh, then
Using Theorem 4.5 and Theorem 4.7 we have
By the use of Theorem 4.8, we can see that
Combining (19) and (20) we have
where
since  .
.
□
From Theorem 4.9, applying inverse estimates and the very classical interpolation results presented in, for example, Chapter 3 of [5], we obtain the following error estimate
with c1, c2∈ 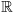 , uh∈
, uh∈  (Ω) and ph ∈
(Ω) and ph ∈  (Ω) and | · |m+1 the semi-norm ofthe Wm,2(Ω).
(Ω) and | · |m+1 the semi-norm ofthe Wm,2(Ω).
5 Numerical results
In order to obtain numerical results for the finite element method presented here to nonlinear problem, the following numerical algorithm will be used. There are many methods to solve nonlinear equations. In this case, we lag nonlinear terms in the system of equations and start with an initial guess generating a sequence of functions that is expected to converge for the solution. In this sense, our scheme is constructed by: given  ∈ Vh, lets find
∈ Vh, lets find  ∈ Vh × Wh, n = 1, 2, 3, ... such that
∈ Vh × Wh, n = 1, 2, 3, ... such that
The algorithm above, was applied to obtain numerical results for the classical driven cavity flow problem with bounbary conditions: u(x) = (1, 0) on x ∈ [0, 1] × {1} and u(x) = (0, 0) on the other boundaries. A finite element mesh of 17 × 17 nodes and 8 × 8 biquadratic quadrilateral elements has been used. The numerical results were performed using the following stabilizing parameters: δ1 = 1.0 and δ2 = 10.0. For the convergence of the algorithm, we imposed a tolerence of 10-6. Numerical results are shown for some combinations of the constitutive parameters λ1 and λ2. In Figure 1 we can note the characteristic of the pseudoplastic behavior comparing the velocity profiles on x = 0.5 for the λi combinations presented. Velocity and pressure fields are shown in Figures 2-4 for the same λi combinations of those in Figure 1. We can see, from these results, how λ1 and λ2 control the Newtonian and the pseudoplastic contributions respectively. We note magnitude decreasing in the velocity and in the pressure fields and also the flatteness of the pressure next to the two corners (0, 1) and (1, 1) due to the pseudoplastic effect, as expected. Formulations that use the continuous pressure interpolations may present lack of accuracy in those regions, where critical boundary conditions exist. Unlike, discontinuous pressure interpolations, as is the case here, recover the accuracy at those regions, due to the satisfaction of the incompressibility constraint locally. The convergence behaviour of the algorithm used, together with the Petrov-Galerkin-like formulation PGhd, is shown in Figure 5, as a function of the α power index for four Sisko fluids. It can be seen that the greater is the non-Newtonian effect, the larger is the number of iteractions required to achieve convergence, as expected for a fixed mesh. Note that even for a higher nonlinearity (higher power index α) convergence and stability are achieved.
6 Summary and conclusions
In this work, a consistent stabilized mixed Petrov-Galerkin-like finite element formulation in primitive variables, with continuous velocity and discontinuous pressure interpolations, has been mathematically analyzed for flows governed by the nonlinear Sisko relation. Stability, convergence and error estimates have been proven for same order interpolations of the primitive variables for any combinations when k > 2.
To generate the mathematical stability conditions, it was possible to split the discontinuous pressure. Only the constant by part pressure resulted as responsible to fulfill the LBB condition. The other part, the null mean pressure part, contributed to achieve the required ellipticity in the Scheurer's theorem sense together with the stabilizing terms. For this formulation ellipticity was the key for the stability, since the constant part of the pressure fulfills in standard ways the LBB. It was possible from the ellipticity to provide a sufficient condition to choose the stabilizing parameters not only as a function of the quasi-newtonian constitutive parameter but considering both constitutive constants coming from the Sisko relation.
Numerical results have been presented for the benchmark driven cavity flow problem to confirm the mathematical analysis.
From the results, stability and convergence have been reached for several combinations of the constitutive parameters of the Sisko relation, ranging from lower to highly pseudoplastic (low α and/or high λ2) effects, although with more interactions in the last case.
The use of discontinuous pressure interpolations ensured accuracy for the pressure field even in the regions where discontinuous boundary conditions are present, since, now, the weakened internal constraint is satisfied locally, in contrast with continuous approximations.
Received: 10/VIII/10.
Accepted: 10/XI/11.
#CAM-240/10.
- [1] R.A. Adams, Sobolev Spaces Academic Press (1975).
- [2] I. Babuka, Error bounds for finite element method Numerische Mathematik, 16 (1971), 322-333.
- [3] R.B. Bird, R.C. Armstrong and O. Hassager, Dynamics of Polimeric Liquids Wiley, Vol 1 (1987).
- [4] F. Brezzi, On the existence, uniqueness and approximation of saddle-point problems arising from Lagrange multipliers Revue Française d'Automatique Informatique et Recherche Opérationnelle, Ser. Rouge Anal. Numér., 8 (1974), 129-151.
- [5] P.G. Ciarlet, The finite element method for elliptic problems North-Holland(1991).
- [6] M.M. Cross, Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic systems Journal of Colloid Science, 20 (1965), 417-437.
- [7] M. Fortin, Old and new finite elements for incompressible flows International Journal for Numerical Methods in Fluids, 1 (1981), 347-431.
- [8] V. Girault and P.A. Raviart, Finite Element Methods for Navier-Stokes Equations. Theory and Applications Springer-Verlag, Berlin (1986).
- [9] T.J.R. Hughes, The Finite Element Method: Linear Static and Dynamic Finite Element Analysis Dover Publications (2000).
- [10] A.F.D. Loula and J.N.C. Guerreiro, Finite element analysis of nonlinear creeping flow Computer Methods in Applied Mechanics and Engeneering, 79 (1990),87-109.
- [11] J. Karam Filho and A.F.D. Loula, A Non-standard application of Babuka-Brezzi theory to finite element analysis of Stokes problem Computational and Applied Mathematics, 10 (1991), 243-262.
- [12] B. Scheurer, Existence et approximation de points selles pour certains problems non Lineaires Revue Française d'Automatique Informatique et Recherche Opérationnelle, Ser. Rouge Anal. Numér., 11 (1971), 369-400.
- [13] I. Wang and J.F. Stoltz, Influence of non-Newtoninan properties of blood on the global transport of red blood cells Clinical Hemorheology, 14 (1994), 789-796.
Publication Dates
-
Publication in this collection
26 Apr 2012 -
Date of issue
2012
History
-
Received
10 Aug 2010 -
Accepted
10 Nov 2011

























































