Abstract
In this paper, we compute piecewise constant bounds on the solution of mixed nonlinear Volterra-Fredholm integral equations. The enclosures are in the form of intervals which are guaranteed to contain the exact solution considering all round-off and truncation errors, so the width of interval solutions allows us to control the error estimation. An iterative algorithm to improve the accuracy of initial enclosures is given and its convergence are also investigated. Our numerical experiments show that the precision of interval solutions are reasonable in comparison to the classical methods and the obtained conditions and initial enclosure of the proposed algorithm are not restrictive. Mathematical subject classification: 65G20, 45G10, 65G40.
Volterra-Fredholm integral equations; enclosure methods; interval analysis; guaranteed error bounds
Piecewise constant bounds for the solution of nonlinear Volterra-Fredholm integral equations
S. Yazdani; M. Hadizadeh* * Corresponding author.
Department of Mathematics, K.N. Toosi University of Technology, P.O. Box 16315-1618, Tehran, Iran E-mails: yazdanis@sina.kntu.ac.ir / hadizadeh@kntu.ac.ir
ABSTRACT
In this paper, we compute piecewise constant bounds on the solution of mixed nonlinear Volterra-Fredholm integral equations. The enclosures are in the form of intervals which are guaranteed to contain the exact solution considering all round-off and truncation errors, so the width of interval solutions allows us to control the error estimation. An iterative algorithm to improve the accuracy of initial enclosures is given and its convergence are also investigated. Our numerical experiments show that the precision of interval solutions are reasonable in comparison to the classical methods and the obtained conditions and initial enclosure of the proposed algorithm are not restrictive.
Mathematical subject classification: 65G20, 45G10, 65G40.
Key words: Volterra-Fredholm integral equations, enclosure methods, interval analysis,guaranteed error bounds.
1 Introduction
During the last three decades, the role of enclosure methods in numerical solution of operator equations has continuously increased. In many cases computers are not perfect tools in scientific calculations, specially when using floating point arithmetic, the solutions are affected by rounding errors and this may led to completely wrong results (see e.g. [17]). This is more important when increasing the speed of computers and for complicated equations, but its impossible to verify the accuracy of the results by classical schemes. Interval enclosure methods are able to compute guaranteed error bounds including all discretization and round-off errors in the computation. These methods are used in many applied areas e.g. fuzzy set theory, engineering problems with interval valued parameters or interval initial values, robust control, robotics, multimedia architectures [12], economics, beam physics, global optimization, signal processing and computer graphics [11] (see also [1] for a survey on enclosure methods).
Here, we restrict our attention to the computation of guaranteed bounds for the solution of the following nonlinear Volterra-Fredholm integral equation of mixed type
where u(x, t) is an unknown function, and f(x, t) and k(x, t, ξ, τ, u(ξ, τ)) are known analytic functions defined on
(where S: = {(x, t, ξ, τ): 0 < τ < t < χ; (x, ξ) ∈ Ω × Ω}), with k(x, t, ξ, τ, u) nonlinear in u and Ω is closed subset of  d (d = 1, 2, 3).
d (d = 1, 2, 3).
These equations play an important role for abstract formulation of many initial or boundary value problems of perturbed differential equations, nonlinear parabolic partial differential equations and partial integro-differential equations which arise in various applications like the mathematical modeling of chemical reaction kinetics, population dynamics [25], heat-flow in material with memory, electromagnetics [10], viscoelastic and reaction diffusion problems.
There has been much work on analyzing and numerical methods for the models consisting of Volterra-Fredholm integral equations. Diekmann and Thieme described and developed some of these models in [7, 24]. The existence and uniqueness of the global solution of the equations have been investigated by Burton [4] and Dhakne et al. [6]. Also some of the schemes which have considered the solution of the linear and nonlinear cases of (1.1) numerically are projection methods, continuous time and discrete time spline collocation method [2, 16], Euler Nystrom and trapezoidal Nystrom methods [13], the Adomian decomposition method [18], the time-stepping methods by a certain choice of direct quadrature (DQ) [3] and Sinc collocation method based on DE transformation in [14]. Generally, all of these classical methods are efficient and effective, but in many cases most of them are unable to control the truncation and round off errors in numerical computations. Here, our aim is to use an interval scheme which considers such these apparent errors.
As we know, there are not any considerable interval based works in solving mixed Volterra-Fredholm integral equations. Moore [19] has introduced an iterative algorithm for nonlinear integral equations based on the definition of interval integration. Caprani et al. [5] and Dobner [9] proposed several papers on solving Fredholm integral equations using enclosure methods. Recently, Murashige and Oishi [21] presented numerical verification of solutions of periodic integral equations with a singular kernel and Nekrasov's integral equation. In comparison to Fredholm type, there are a few enclosure methods on solving Volterra integral equations especially in the nonlinear form [8, 15].
In the present work, we propose an algorithm to provide piecewise constant bounds for the solution of nonlinear Volterra-Fredholm integral equations. Our algorithm is based on the early idea of Moore [19] for Volterra integral equations. The organization of this paper is as follows: In section 2, we give basic notation, definitions and a summary on the principles of interval arithmetic. A new enclosure is constructed from an initial bound and its properties are studied in section 3 and then an iterative algorithm for the computation of piecewise constant bounds including its convergence conditions is presented. Finally, numerical experiments and a full discussion on initial enclosure, the algorithm conditions and also the number of iterations are reported to clarify the efficiency of the method.
2 Notations and auxiliary results of the interval theory
2.1 Interval arithmetic
We first introduce some basic properties of interval arithmetic from [20, 22, 23]. The set of compact real intervals is denoted by
Through out of this paper, using the notation of [23], intervals are denoted by boldface and lowercase letters are used for denoting scalars and vectors. A real number x is identified with a point interval x = [x, x]. The quality of interval analysis is measured by the width of the interval results, and a sharp enclosure for the exact solution is desirable. The midpoint and the width of an interval x are denoted by
respectively. The width of an interval vector x = (x1, ..., xn) is the largest of the widths of any of its component intervals
Considering |x| = max{|x|,|[ ]}, for any x,y ∈
]}, for any x,y ∈  and a, b ∈
and a, b ∈  , we get the following properties:
, we get the following properties:
The four elementary operations of real arithmetic can be extended to intervals. Operations over intervals ◊ ∈ {+, -, ∗, /} are defined by the general rule
It is easy to see that the set of all possible results when applying an operator ◊ to x and y, forms a closed interval (for 0 ∉ y in the case of division) and the end point can be calculated by
The following lemma gives an important property which is used frequently in this paper:
Lemma 1. Let k = [k, 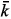 ] and y = [0,
] and y = [0, 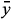 ], also there exists a constant α >1, such that |k| < α ω (k), then
], also there exists a constant α >1, such that |k| < α ω (k), then
Proof. We consider the following three cases:
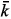 , then ω(ky) = ω([k
, then ω(ky) = ω([k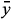 ,
, 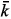
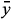 ]) =
]) = 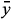 (
(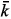 - k) < αω(k)
- k) < αω(k)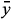 .
.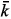 < 0, then ω(ky) = ω([k
< 0, then ω(ky) = ω([k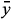 , 0]) = |k|
, 0]) = |k|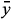 < |k|
< |k|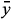 < αω(k)
< αω(k)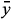 .
.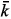 , then ω(ky) = ω([0,
, then ω(ky) = ω([0, 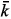
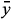 ]) = |
]) = |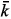 |
|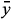 < |k|
< |k|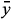 < αω(k)
< αω(k)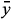 , and the proof is complete.
, and the proof is complete.2.2 Preliminaries
Most of the following information regarding the interval functions may be found in [20], but here we recall certain points that are important for establishing and analyzing the accuracy of our new enclosures from [23] and [19]:
Let f be a real valued function of several variables, we can define set image or the united extension of f as:
Functions of interval variables are often computed by substituting the given interval x for x in f(x) and then evaluating the function using interval arithmetic. An interval extension of f is an interval valued function F of n interval variables x1,..., xn such that for real arguments x1,..., xn we have
This natural interval extension is sometimes wider than the actual range of function values, though it always includes the actual range e.g. let f(x) = x/(1 + x), then f([1,2]) = [1/2, 2/3], but natural interval extension of f is F([1, 2]) = [1/3, 1] which is wider than [1/2, 2/3]. To overcome this difficulty so called dependency effect, some alternative schemes such as mean value form and Taylor enclosures are proposed in [20] and [5].
Definition 1 [20] An interval extension F is said to be Lipschitz interval extension in x0, if there is a constant L, such that w(F(x))< L ω(x), for every x ⊆ x0.
Therefore, the width of F(x) approaches zero at least linearly with the width of x. Here x may be an interval or an interval vector.
Definition 2 [20] An interval valued function F(x1,...,xn) is called inclusion isotonic, if for yi⊆ xi, i = 1,..., n we have
Definition 3 [20] A rational interval function is an interval-valued function whose values are defined by a specific finite sequence of interval arithmetic operations.
Lemma 2 [20] If F is a natural interval extension of a real rational function with F(x) defined for x ⊆ x0, where x and x0 are intervals or n-dimensional interval vectors, then F is Lipschitz in x0.
Lemma 3 [20] Let F and G be inclusion isotonic interval extensions with F Lipschitz in Y0, G Lipschitz in x0, and G(x0) ⊆ Y0, then the composition H(x) = F(G(x)) is Lipschitz in x0 and be inclusion isotonic.
Lemma 4 [20] If F is a rational interval extension of a real function f, and (x1,..., xn) ∈ (x1,..., xn) then f(x1,..., xn) ∈ F(x1,..., xn).
A well known definition of the interval extension of a real integral has been introduced by Moore [19] which is defined as follows:
where F is interval extension of f.
3 Computation of piecewise constant bounds
In order to compute piecewise constant bounds for the solution of a nonlinear Volterra-Fredholm integral equation (1.1), we first subdivide the intervals [0, χ] and Ω = [a, b] by points
where px and pt are number of subdivisions. Now, considering an initial enclosure u0 =  , which is assumed to contain the exact solution of the equation in whole interval, a new enclosure in each subinterval will be obtained.
, which is assumed to contain the exact solution of the equation in whole interval, a new enclosure in each subinterval will be obtained.
Suppose that the real valued function f(x, t) in (1.1) is continuous and k(x, t, ξ, τ, u(ξ, τ)) satisfies a Lipschitz condition with respect to u for all (x, t, ξ, τ, u(ξ, τ)) in S × , also F(xi, tj) and K(x, t, ξ, τ,u0)) are natural interval extensions of f and k. Hence using Lemmas 2.2 and 2.2 and considering LF as a Lipschitz constant, we conclude F(xi, tj) is Lipschitz in [0, χ] × Ω, so
, also F(xi, tj) and K(x, t, ξ, τ,u0)) are natural interval extensions of f and k. Hence using Lemmas 2.2 and 2.2 and considering LF as a Lipschitz constant, we conclude F(xi, tj) is Lipschitz in [0, χ] × Ω, so
where Lδ = max{ω(xi), ω(tj)}. Also, there exist a Lipschitz constant Lk such that for all x, ξ ∈ [0, χ], and t, τ ∈ Ω, we have
In the following, we introduce the new enclosure and give some of its important properties:
Lemma 5.Let u(x, t) ∈ u0 =  and for x ∈ xi = [xi - 1, xi], ξ ∈ xl, 1 < l < i < px, and t ∈ tj = [tj - 1, tj], τ ∈ tk, 1 < k < j < pt, we have f(x, t) ∈ F(xi, tj), k(x, t, ξ, τ, u(x, t)) ∈ K(xi, tj, xl, tk, u0), then we can obtain a new enclosure for each
and for x ∈ xi = [xi - 1, xi], ξ ∈ xl, 1 < l < i < px, and t ∈ tj = [tj - 1, tj], τ ∈ tk, 1 < k < j < pt, we have f(x, t) ∈ F(xi, tj), k(x, t, ξ, τ, u(x, t)) ∈ K(xi, tj, xl, tk, u0), then we can obtain a new enclosure for each  as
as
Proof. Let us assume x ∈ xi and t ∈ tj in each subinterval, then the equation (1.1) can be written as
Considering Lemma 2.2, we get f(x, t) ∈ F(xi, tj) and k(x, t, ξ, τ, u(x, t)) ∈ K(xi,tj, xl, tk,u0). Now using (2.3) and the assumptions of the lemma, we replace x and t by xi and tj in each subinterval, respectively, to obtain the following interval enclosure
Note that
so the equation (3.4), can be written as
In this position, we give an important property of the proposed guaranteed bounds which implies that u1,i,j is an efficient enclosure in comparison to u0 in each subinterval (xi, tj):
Theorem 1. Assume that max{ω(xi), ω(tj)}< ω(u0) and there exist LF, Lk such that
then the new enclosure presented by (3.3) has less width in comparison to initial enclosure u0.
Proof. Following (2.1), (2.1) and using (3.3), we find that
Now, using (3.1), (3.2) and Lemma 1, we have
and
so
Finally the condition
gives
Remark. We will show later in Section 4, the condition θ < 1 in (3.6) is not restrictive in practice and in most cases (3.7) is easily established.
It is well known, in many cases interval initial enclosure may be much wider than the real solution. In order to construct a narrow interval solution, we apply Theorem 1 and consider u1,i,j ∩ u0 as a new approximation for u(x). This can be substituted in right side of (3.3) for u0 to give the next approximation and the process is then repeated to achieve a rigorous solution.
Moreover, since the points of subdivision (xi, tj) for i = 1,..., px, j = 1,..., pt interior to [a, b] ×Ω are common endpoints of boxes xi × tj, xi ×tj + 1, xi + 1 × tj and xi + 1× tj + 1, therefore we have
The following algorithm summarizes our strategy where the notations px and pt are the number of subdivisions in [0, χ] × Ω and n is number of iterations:
Algorithm: Computation of piecewise constant bounds
COMPUTE:
OUTPUT:
Oi,j
Noting that, Theorem 1 shows that the new enclosures are more efficient in comparison to initial bounds, especially when the number of subdivisions is increased. So, in many cases just a few number of iterations is needed in practice and the method rapidly reaches the appropriate solutions.
The convergence of the proposed algorithm can be characterized by the following theorem:
Theorem 2. Under the hypotheses of Theorem 1, the proposed algorithm is convergent.
Proof. From (3.5), we get
Substituting u0 by u1,i,j in (3.3) and using Theorem 1 and relation (3.8), the next enclosure u2,i,j will be obtained as
Continuing the process, we get
Now, according to  , we conclude
, we conclude
4 Numerical experiments and discussions
Here, we consider two test problems and report the numerical results by the proposed method. Moreover, an adequate discussion on the efficiency of the algorithm is presented. Our discussion includes features and limitations of the scheme e.g. the problem of selecting initial enclosure, the number of iterations and subdivisions. All computations are performed by using the symbolic calculations software Mathematica®.
Example 1. [18] Consider the following nonlinear Volterra-Fredholm integral equation
where Ω = [0, 1] and the exact solution is
We analyze the problem in three main parts. At first, we compute piecewise bounds on the solution and a comparison is made between the widths of interval solutions and the results of existing classical methods. Then, we show that the conditions of the algorithm and the initial enclosure are not restrictive.
1. Computing piecewise constant bounds: Solution of the equation based on the proposed algorithm for u0 = [-1, 1] and px = pt = 16 is summarized in Table 1 and Figures 1, 2 for just two iterations. Also, a comparison is made with the numerical results obtained in [18].
The reported results in Table 1 show that since these enclosures include all round-off errors in the computation, interval methods are valuable tools in comparison to classical schemes. Figure 1 indicates that increasing the number of subdivisions led to better numerical results.
5 Discussion on the convergence conditions
The following table gives an approximation for Lk and LF in (3.1) and (3.2):
Analyzing the results of Table 2 shows that the conditions (3.7) and (3.9) are easily established. In some cases, due to the dependency effect the width of F and K may be wider than usual, so as previously mentioned, we can use mean value form or other Taylor enclosures for F and K. For example in Table 2, LF = 0.66 for ([0.4, 0.5], [0.4, 0.5]) is obtained by using the mean value form of F. (For more detail see e.g. [20]).
6 Discussion on u0 and number of iterations
The problem of choosing initial enclosure u0 seems to be another restrictive difficulty. Table 3 illustrates the piecewise bounds obtained by choosing various initial enclosures and number of iterations:
Our experimental results in Table 3, show
(i) If the computed interval is empty (as for u0 = [2, 3]), it implies that we choose an inaccurate u0 which does not contain exact solution.
(ii) If we choose a proper u0 just a few iteration is needed to achieve rigorous solutions, moreover increasing the number of iterations can offset inappropriate u0.
Example 2. [14]
where Ω = [0, 1] and u(x, t) = xt.
Solution of the equation using the proposed scheme is enclosed in intervals as we show in Table 4 and Figures 3, 4. The following experiments are also observed:
(i) Similar to the previous example, for an inaccurate u0 = [-2, -1] the computed interval is empty.
(ii) In many cases, increase the number of iterations does not affect the accuracy of the results, therefore to increase the accuracy we need to increase the number of subdivisions (see e.g. Figure 4).
7 Conclusion
Nonlinear Volterra-Fredholm integral equations have many applications in science and engineering, but in many cases, accumulation of truncation and round-off errors prevent the numerical methods to converge to the exact solution. In this paper, we consider an initial enclosure and obtain a new guaranteed bounds for the solution of these equations including all round-off and truncation errors. We also clarify that the algorithm initial enclosures and conditions are not restrictive in practice. Our numerical experiments show that the exact solution is enclosed in intervals where the width of intervals gives the accuracy of the numerical results. This is of great importance, especially when the equations are complicated and the solution is not determined analytically or numerically.
Received: 12/V/11.
Accepted: 02/I/12.
#CAM-370/11.
- [1] G. Alefeld and G. Mayer, Interval analysis: theory and applications J. Comput. Appl. Math., 121 (2000), 421-464.
- [2] H. Brunner, On the numerical solution of nonlinear Volterra-Fredholm integral equation by collocation methods SIAM J. Numer. Anal., 27 (1990), 987-1000.
- [3] H. Brunner and E. Messina, Time-stepping methods for Volterra-Fredholm integral equations by collocation methods Rend. Math., 23 (2004), 329-342.
- [4] T.A. Burton, Volterra Integral and Differential Equations Academic Press, New York (1983).
- [5] O. Caprani, K. Madsen and O. Stauning, Enclosing solutions of integral equations Technical Report, Tech. Univ. of Denmark (1996).
- [6] M.B. Dhakne and S.D. Kendre, On abstrct nonlinear mixed Volterra-Fredhom integro-differential equations Comm. Appl. Nonlinear Anal., 4 (2006), 101-112.
- [7] O. Diekmann, Thresholds and travelling waves for the geographical spread of infection J. Math. Biol., 6 (1978), 109-130.
- [8] H.J. Dobner, Computing narrow inclusions for the solution of integral equations Numer. Func. Anal. Optim., 10 (1989), 923-936.
- [9] H.J. Dobner, A method for estimating the solution of integral equations encountered in potential theory Appl. Math. Comput., 109 (2000), 199-204.
- [10] K. Domke and L. Hacia, Integral equation in some thermal problem Int. J. Math. Comput. Simulation, 2 (2007), 184-189.
- [11] W. Edmonson, S. Ocloo, C. Williams and W. Alexander, The use of interval methods in signal processing and control for systems biology edmonson, Foundations of Computational Intelligence, IEEE Symposium (2007), 136-142.
- [12] J.W.V. Gudenberg, Interval arithmetic on multimedia architectures Reliab.Comput., 8 (2002), 307-312.
- [13] H. Guoqiang, Asymptotic error expansion for the Nystrom method for a nonlinear Volterra-Fredholm equations J. Comput. Appl. Math., 59 (1995).
- [14] M. Hadizadeh and Gh. Kazemi, Error estimate in the Sinc collocation method for the Volterra-Fredhlom integral equations based on DE Transformation Elect.Trans. Numer. Anal., 30 (2008), 75-87.
- [15] M. Hadizadeh and S. Yazdani, New enclosure algorithms for the verified solutions of nonlinear Volterra integral equations Appl. Math. Modelling, 35 (2011), 2972-2980.
- [16] J.P. Kauthen, Continuous time collocation methods for Volterra-Fredholm integral equations Numer. Math., 56 (1989), 409-424.
- [17] J.L. Lions, Ariane 5, flight 501 failure Technical report, European Space Agency (1996).
- [18] K. Maleknejad and M. Hadizadeh, A new computational method for Volterra-Fredholm integral equations Computer Math. Applic., 37 (1999), 1-8.
- [19] R.E. Moore, Interval Analysis Prentice-Hall, New York (1966).
- [20] R.E. Moore, R.B. Kearfott and M.J. Cloud, Introduction to Interval Analysis SIAM (2009).
- [21] S. Murashige and S. Oishi, Numerical verification of solutions of periodic integral equations with a singular kernel Numer. Algor., 37 (2004), 301-310.
- [22] R. Muhanna, H. Zhang and R. Mullen, Interval finite elements as a basis for generalized models of uncertainty in engineering mechanics Reliab. Comput., 13 (2007), 173-194.
- [23] M. Neher, K.R. Jackson and N.S. Nedialkov, On Taylor model based integration of ODES. SIAM J. Numer. Anal., 45 (2007), 236-262.
- [24] H.R. Thieme, A model for the spatial spread of an epidemic, 4 (1977), 337-351.
- [25] H.L. Tidke, Existence of global solutions to nonlinear mixed Volterra-Fredholm integro-differential equations with nonlocal conditions Electron. J. Diff. Equa., 55 (2009), 1-7.
Publication Dates
-
Publication in this collection
05 Dec 2012 -
Date of issue
2012
History
-
Received
12 May 2011 -
Accepted
02 Jan 2012


















































