Abstract
This paper presents the numerical analysis of the Nonlinear Subgrid Scale (NSGS) model for approximating singularly perturbed transport models. The NSGS is a free parameter subgrid stabilizing method that introduces an extra stability only onto the subgrid scales. Thisnew feature comes from the local control yielded by decomposing the velocity field into the resolved and unresolved scales. Such decomposition is determined by requiring the minimum of the kinetic energy associated to the unresolved scales and the satisfaction of the resolved scale model problem at element level. The developed method is robust for a wide scope of singularly perturbed problems. Here, we establish the existence and uniqueness of the solution, and provide an a priori error estimate. Convergence tests on two-dimensional examples are reported. Mathematical subject classification: Primary: 65N12; Secondary: 74S05.
subgrid modeling; nonlinear subgrid viscosity; advection-diffusion-reactionequations
Numerical analysis of the nonlinear subgrid scale method
I.P. SantosI; R.C. AlmeidaII; S.M.C. MaltaII
IUniversidade Federal do Espírito Santo - UFES/CEUNES. E-mail: isaacsantos@ceunes.ufes.br
IILaboratório Nacional de Computação Científica. E-mails: rcca@lncc.br / smcm@lncc.br
ABSTRACT
This paper presents the numerical analysis of the Nonlinear Subgrid Scale (NSGS) model for approximating singularly perturbed transport models. The NSGS is a free parameter subgrid stabilizing method that introduces an extra stability only onto the subgrid scales. Thisnew feature comes from the local control yielded by decomposing the velocity field into the resolved and unresolved scales. Such decomposition is determined by requiring the minimum of the kinetic energy associated to the unresolved scales and the satisfaction of the resolved scale model problem at element level. The developed method is robust for a wide scope of singularly perturbed problems. Here, we establish the existence and uniqueness of the solution, and provide an a priori error estimate. Convergence tests on two-dimensional examples are reported.
Mathematical subject classification: Primary: 65N12; Secondary: 74S05.
Key words: subgrid modeling, nonlinear subgrid viscosity, advection-diffusion-reactionequations.
1 Introduction
It is known that some numerical difficulties arising in the simulation of advection-dominated and reaction-dominated problems are due to the presence of considerable information contained in small scales and whose effects are notrepresented on the large ones. In these cases, the smallest scales of the grid are not fine enough for the viscous dissipation to be effective yielding a kinetic energy accumulation [1,23,29] . To rectify these difficulties, different methodologies have been developed in the literature. The most common approach is known as stabilized methods [4,7,9,18,24] . These methods add to the Galerkin formulation perturbation terms associated to the operator and containing stabilizing parameters dependent on the mesh. In essence, they add some sort of artificial dissipation to avoid energy accumulation. The accuracy and stability of the solutions obtained with these methodologies depend on a suitable design of the stabilization parameter(s) [4,9,15,18] . More recently, stabilized methods have been reformulated in the context of the variational multiscale formulation [17,19] and a number of variational methods for problems exhibiting multiscale behavior have been developed in the last years [3,6,8,11,12,14,16,17,20,30] . Also, it is worth mentioning that linear methods are usually not able to remove localized spurious oscillations for nonsmooth solutions. The well known remedy, from the point of view of stabilized methods, is to add a nonlinear term to the linear formulation to enhance stability, usually called discontinuity or shock capturing term, which is tuned by stabilized parameters. A detailed review on the most used shock capturing models is presented in [21] , in which it is emphasized the important role the stabilized parameters play in the stability and accuracy of the approximate solution. Here, we present the numerical analysis of the nonlinear subgrid scale method (NSGS) proposed in [25] . This method is based on the linear subgrid scale method (SGS) developed by J.-L. Guermond in [12,13] . The latter procedure is built by splitting the approximation space into resolved and unresolved (subgrid) scales so that the bilinear form associated with the problem satisfies a uniform inf-sup condition with respect to this decomposition [13] . It also introduces an artificial diffusion subgrid stabilizing term that depends on the choice of an heuristic parameter. Its correct choice is crucial to yield accurate solutions, although the criteria for choosing it have been based on a trial and error strategy [14] . Despite this, the subgrid scale approach is quite simple and appealing [2] since it may be applied to a great variety of problems. In this context, the NSGS was developed with the aim of determining the amount of subgrid dissipation according to the problem, in order to yield a free parameter method. Unlike other multiscale methods [14,22,27] , the NSGS adds to the Galerkin bilinear form a nonlinear subgrid term and does not maintain any other linear operator. The amount of subgrid viscosity is tuned locally according to the residual of the resolved scale at the element level.
The NSGS method was originally proposed in [25] for advection dominated advection-diffusion problems. The version presented here recovers the Galerkin method if the resolved scale solution is accurate enough, resulting in more stable solutions. The method was also shown to be stable for reaction dominated reaction-diffusion problems.
In this paper we establish the numerical analysis of the NSGS method, following the approach used in [13] . The convergence properties are shown to be similar to the SGS method as well as the SUPG method.
The outline of this paper is as follows. We briefly address the basic concepts of the NSGS model in Section 2. In Section 3 we present existence, uniqueness and error estimates for the discrete problem. Numerical examples are conducted in Section 4 and in the last section we draw some conclusions.
2 The nonlinear subgrid stabilization
The advection-diffusion-reaction problem can be modeled by the followingequation
where Ω ⊂ ℜd, 1 < d < 3, is an open bounded domain with a Lipschitz boundary ∂Ω and unit outward normal n, β is the velocity field, σ is the reaction coefficient, 0 < ε  1 is the (constant) diffusion coefficient and f is the source term. Henceforth, it is assumed that β ∈ [L∞ (Ω)] d, σ ∈ L∞ (Ω) andf ∈ L2 (Ω). It is also assumed that σ > 0 and there exists a constant σ0 such that
1 is the (constant) diffusion coefficient and f is the source term. Henceforth, it is assumed that β ∈ [L∞ (Ω)] d, σ ∈ L∞ (Ω) andf ∈ L2 (Ω). It is also assumed that σ > 0 and there exists a constant σ0 such that
For simplicity, we set only homogeneous Dirichlet boundary conditions that will be strongly enforced. Denoting by (·, ·) the L2(Ω) inner product, the classical formulation of problem (1)-(2) reads: find u ∈ X =  (Ω) so that
(Ω) so that
where
The Lax-Milgram Lemma proves that there is a unique solution to the problem (4). The operator B(u, v) is coercive although it can lose coercivity if the diffusion coefficient is small enough. Cases of this type are considered in this work, such that the Galerkin approximation of (4) based on Xh ⊂ X may be completely worthless. This can be rectified by using a simple dissipation model as the one developed in [12,13] - the SGS method, which has its roots in the scales separation. In a two-scale approach there is a pair of spaces {XH, Xh}, XH ⊂ Xh, which satisfies the following multiscale decomposition [12,13]
where XH is the resolved (coarse) scale space whereas  is the subgrid(fine) scale space. One possible artificial dissipation mechanism proposed in [12,13] is
is the subgrid(fine) scale space. One possible artificial dissipation mechanism proposed in [12,13] is
where  ∈
∈  is the subgrid scale of the approximate solution,
is the subgrid scale of the approximate solution,  ∈
∈  is the subgrid scale of the weight function and
is the subgrid scale of the weight function and  b is the (user-specified) subgrid scale artificial diffusion coefficient. The operator (8) is added to (4), yielding an additional control of the subgrid scales. However, the effectiveness of this formulation is strongly dependent on the choice of
b is the (user-specified) subgrid scale artificial diffusion coefficient. The operator (8) is added to (4), yielding an additional control of the subgrid scales. However, the effectiveness of this formulation is strongly dependent on the choice of  b. The NSGS (Nonlinear Subgrid Scale Method) [25] was built to overcome this difficulty and can be seen as a nonlinear counterpart of the SGS method. In this approach, the subgrid artificial diffusion is adaptively determined as a function of the accuracy of the resolved scale solution, yielding a free parameter subgrid scale method. The general construction of the method is shown below. For more details, see [25,26] .
b. The NSGS (Nonlinear Subgrid Scale Method) [25] was built to overcome this difficulty and can be seen as a nonlinear counterpart of the SGS method. In this approach, the subgrid artificial diffusion is adaptively determined as a function of the accuracy of the resolved scale solution, yielding a free parameter subgrid scale method. The general construction of the method is shown below. For more details, see [25,26] .
To define the discrete problem, let
h = {Th} and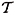 H = {T} denote two triangular regular partitions of the domain Ω, where the subscripts h and H stand for the characteristic mesh length of each mesh, respectively. The spaces XH and Xh are conforming finite element spaces on
H = {T} denote two triangular regular partitions of the domain Ω, where the subscripts h and H stand for the characteristic mesh length of each mesh, respectively. The spaces XH and Xh are conforming finite element spaces on 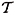 H and
H and 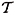 h, respectively. The NSGS method can be described as follows:
h, respectively. The NSGS method can be described as follows:
where the (local) nonlinear subgrid operator
is given by
The subgrid artificial viscosity εk is designed to be the smallest one that is able to avoid kinetic energy accumulation associated with the unresolved scales, denoted by Ek. A key ingredient for the εk design is the two-level decomposition of the velocity field in the form
whereβH and  are the velocity fields related to the resolved and the subgrid scales, respectively. The decomposition (11) allows representing the kineticenergy related to small scales by Ek =
are the velocity fields related to the resolved and the subgrid scales, respectively. The decomposition (11) allows representing the kineticenergy related to small scales by Ek =  |
| |2. Thus, if we denote the subgrid length scale by
|2. Thus, if we denote the subgrid length scale by  , it is possible to determine the subgrid time scale at which the subgrid inertial effects take place as t =
, it is possible to determine the subgrid time scale at which the subgrid inertial effects take place as t =  /|
/| |. With these assumptions, the amount of subgrid viscosity required to dissipate the kinetic energy Ek may be defined as
|. With these assumptions, the amount of subgrid viscosity required to dissipate the kinetic energy Ek may be defined as
One may set  = h = (measTh)1/d, as assumed in [12,13] , although other choices are possible. The subgrid velocity field
= h = (measTh)1/d, as assumed in [12,13] , although other choices are possible. The subgrid velocity field  is determined by assuming that the residual of the resolved scale solution (usingβH) at each element level vanishes and, among all possible subgrid scale velocity fields,
is determined by assuming that the residual of the resolved scale solution (usingβH) at each element level vanishes and, among all possible subgrid scale velocity fields,  yields minimal kinetic energy Ek. The solution of this minimization problem may be found through the minimun of the functional
yields minimal kinetic energy Ek. The solution of this minimization problem may be found through the minimun of the functional
where λ is a Lagrange multiplier. The stationary condition for this functional leads to
Since R(uH) = - ε ΔuH +β · ∇uH + σuH - f, a simple algebrism yields
Then, given definitions (12) and (9), we design the method by considering the following two cases:
(1) when |∇uH| = 0, which implies |R(uH)| = 0, we have |
| = 0 so that A(uh, vh) = B(uh, vh), recovering the Galerkin method. In this case, the Galerkin formulation is coercive enough and no extra stability termis needed;
(2) when |∇uH| ≠ 0, we obtain
This means that an extra dissipation mechanism is added to the Galerkin formulation so that
characterizing the enhancement of the stability throughout the subgrid term. Notice that the subgrid artificial viscosity depends on the resolved scale solution in the following way
The non-linear formulation (9) is solved using a quite simple iterative procedure in which εk (or  ) is delayed one iteration. The initial guess is built solving (9) with εk = (measTh)1/d, independently of ∇uH, which amounts to using the SGS method [12] with
) is delayed one iteration. The initial guess is built solving (9) with εk = (measTh)1/d, independently of ∇uH, which amounts to using the SGS method [12] with  b = (measTh)1/d. It is important to remark that this choice does not yield any change in the final solution accuracy. The convergence is checked for all the resolved scale degrees of freedom, under a prescribed tolerance (tol), and may decrease with the increase of the distance between two consecutive approximations
b = (measTh)1/d. It is important to remark that this choice does not yield any change in the final solution accuracy. The convergence is checked for all the resolved scale degrees of freedom, under a prescribed tolerance (tol), and may decrease with the increase of the distance between two consecutive approximations  and
and  , where the new superscript denotes the iterative step. We improve convergence by proposing the following average rule to determine the subgrid artificial viscosity:
, where the new superscript denotes the iterative step. We improve convergence by proposing the following average rule to determine the subgrid artificial viscosity:
The existence and uniqueness of the solution of (9) are proved in the next section, and an a priori error estimate is presented as well. This analysis is carried out for the case (2) (|∇uH| ≠ 0) described previously, which characterizes the nonlinear model. Otherwise, when |∇uH| = 0, the Galerkin formulation is recovered as well as its properties.
Remark 2.1. As reported in [25] , the NSGS stabilization term has roots in the nonlinear discontinuity capturing term developed in [10] . However, while the latter is built based on designing an approximate upwind direction, the key ingredient in the former is based on scale separation of the velocity field, so that the resulting artificial diffusion depends only on the resolved scale degrees of freedom. Moreover, another remarkable difference is that the proposed two-scale framework yields a method free of stabilization parameter and no extra linear stabilization term.
Remark 2.2. The formulation (9) with the nonlinear operator defined by (10) is a slight improvement in the original design proposed for the NSGS method in [25] , where the SGS method was kept in the variational form if |∇uH| = 0. In the present version, case (1) allows recovering the Galerkin method when the gradient of the resolved scale solution vanishes. See [26] for further details.
3 Numerical analysis
As usual, ||·||0, ||·||m and |·|∞ denote the standard Sobolev norms of L2 (Ω), Hm (Ω) and L∞ (Ω), respectively. Similarly, we use ||·||0,R, ||·||m,R and |·|∞,R to denote their restriction to a region R ⊂ Ω. Throughout this paper we use c > 0 as a generic constant that does not depend on (H, h) and whose value may change in different situations.
We assume that the discrete counterpart of the bilinear form B(·, ·) (4) satisfies the following continuity and coercivity properties: there exist positive constants α1 and α2 such that
The proof follows directly from the definition of the bilinear form and condition (3) and is therefore omitted. We will also make the following assumptions [13] :
(A1) Approximation property on XH: For given u ∈ Hk + 1(T), k > 0, there exists wH ∈ XH such that
(A2) There is a linear projection operator PH : Xh → XH that is L2(T) -stable:
For all vh ∈ Xh we set vH = PHvh and
= (I - PH)vh, where I is the identity operator;
(A3) Inverse estimate in Xh : ∀vh ∈ Xh and ∀T ∈
H, the following inverse inequality holds:
(A4) Discrete inf-sup condition: There are two constants ca > 0 and cδ > 0, such that ∀T ∈
H
where as(u, v) = (a(u, v) + a(v, u))/2 is the symmetric part of a(u, v). This inequality is important to establish optimal error estimates for the problem and it is satisfied by some commonly used approximating elements. See [12] for details. In the two-dimensional numerical experiments performed in Section 4, we use the two-level
1setting [12] that amounts to consider two nested triangular meshes,
H and
h, with h = H/2, such that each triangle T ∈
H contains four sub-triangles Th of
h formed by connecting the middle of the three edges of T. With this choice, the unresolved solution necessarily vanishes at the three vertices of each element of
H.
The main feature of the NSGS method (9) is its ability to capture discontinuities by introducing the subgrid scales and controlling them by the artificial viscosity operator D(uH,  ,
,  ). It depends on the quantity |
). It depends on the quantity | | which is assumed to satisfy
| which is assumed to satisfy
with q0, q1 > 0. This inequality is always true since |∇uH| ≠ 0 and follows directly from the definition of the subgrid velocity field (16). The previous inequality implies
and
yielding the following coercivity and continuity properties
Next we define the following norm
In order to prove the solution uniqueness, the minimum condition for the subgrid artificial diffusion is required, which comes from definition (18). Notice that when |∇uH| ≠ 0 we obtain | | = |β-β H| = |R(uH)|/|∇uH|, which ensures that, in each element T,
| = |β-β H| = |R(uH)|/|∇uH|, which ensures that, in each element T,  βH =β. Moreover, as
βH =β. Moreover, as  is selected such as to minimize ||β-βH||0,T, the following inequality holds
is selected such as to minimize ||β-βH||0,T, the following inequality holds
which means εk(uH) < εk(wH), ∀wH ∈ XH.
The two following Lemmas are also required to estimate the error of the NSGS method.
Lemma 3.1.There exists α > 0 such that  ∈
∈  , ∀(H, h), and ∀T ∈
, ∀(H, h), and ∀T ∈ 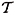 H we have
H we have
Proof. Using (23), (24) and (29) we obtain
yielding the desired result with α = ce2σ2 > 0.
Lemma 3.2.There is c0> 0 such that
Proof. From (3) it follows that
i.e., as(·, ·) is L2-coercive. Then, applying the Cauchy-Schwartz inequality,we have
which leads to the desired result with
The next Lemma is used to prove the existence of the solution uh and is included for clarity. As an extension of the Brouwer Fixed Point Theorem, its proof can be found in [28] (Lemma 1.4 - pp. 164-166).
Lemma 3.3.Let Xh be a finite dimensional Hilbert space with inner product [·, ·] and norm [·] . Let P be a continuous operator from Xh onto Xh such that
for a given l ∈ ℜ+. Then, there exists u ∈ Xh,  < l, such that P(u) = 0.
< l, such that P(u) = 0.
Proposotion 3.4 (Exsitance of uh). Assume that β ∈ [L∞ (Ω)] d, σ ∈ L∞ (Ω) and (21) and (26) hold. Then, there exists a solution uh to (9).
Proof. Define the inner product in Xh ⊂  (Ω) by [u, v] = (∇u, ∇v), with the associated norm [u] = |u|1, and an operator P : Xh → Xh such that
(Ω) by [u, v] = (∇u, ∇v), with the associated norm [u] = |u|1, and an operator P : Xh → Xh such that
The Riesz operator L :  → Xh is such that
→ Xh is such that
with
where  is the dual space of Xh. As B(·, ·) is coercive and D(·, ·, ·) is positive, we have
is the dual space of Xh. As B(·, ·) is coercive and D(·, ·, ·) is positive, we have
Thus [Puh, uh] > 0 if [uh] = l, for a sufficiently large l; more precisely, l >  ||f||0, where cp is the Poincaré constant. As the operator P is continuous (B(·, ·), D(·, ·, ·) and (f, ·) are continuous forms), the hypotheses of Lemma 3.3 hold and hence there exists a solution uh to (9).
||f||0, where cp is the Poincaré constant. As the operator P is continuous (B(·, ·), D(·, ·, ·) and (f, ·) are continuous forms), the hypotheses of Lemma 3.3 hold and hence there exists a solution uh to (9).
The next Proposition establishes the uniqueness of uh. The proof is based on the fulfillment of (32).
Proposition 3.5 (Uniqueness of uh) We assume that there exists a solution uh to (9) and that (3) and (32) hold. Then, uh is unique.
Proof. Assume that there are two solutions  ,
,  ∈ Xh and corresponding resolved and unresolved solutions (
∈ Xh and corresponding resolved and unresolved solutions ( and
and  ;
;  and
and  ). Taking successively uh =
). Taking successively uh =  and uh =
and uh =  in (9) and subtracting the resulting equations, we get
in (9) and subtracting the resulting equations, we get
Choosing vh =  -
-  and using (3), (5) and (6) in the previous equation, we get
and using (3), (5) and (6) in the previous equation, we get
Now, as  and
and  are solutions of (9), it follows from (32) that
are solutions of (9), it follows from (32) that
i.e., εk( ) = εk(
) = εk( ) = α > 0. Thus, we get
) = α > 0. Thus, we get
Hence, (33) and (34) lead to
Therefore, since ε > 0, σ0 > 0 and  -
-  ∈ Xh, we get
∈ Xh, we get
 =
= 
An a priori error estimate for formulation (9) is established by the following theorem. This analysis follows the approach used in [5,13] .
Theorem 3.6. Let u ∈ Hk + 1(Ω) ∩  (Ω) be the solution of (1)-(2). We assume that the assumption (26) holds and ε < H < 1. If uh is the discrete solutionof (9), then
(Ω) be the solution of (1)-(2). We assume that the assumption (26) holds and ε < H < 1. If uh is the discrete solutionof (9), then
Since as(·, ·)|T is L2(T)-coercive (Lemma 3.3), then
where |||·||| is defined in (31).
Proof. Let wH be the interpolant of u in the space XH and let us set
Observing that  = -
= -  and subtracting (9) from (4) taking eh as test function, we obtain
and subtracting (9) from (4) taking eh as test function, we obtain
Using (5), (6) and (30), we obtain
Since as(ηh, eh) =  [a(ηh, eh) + a(eh, ηh)] so that a(ηh, eh) = 2as(eh, ηh) -a(eh, ηh), -B(ηh, eh) can be written as
[a(ηh, eh) + a(eh, ηh)] so that a(ηh, eh) = 2as(eh, ηh) -a(eh, ηh), -B(ηh, eh) can be written as
The first term on the right-hand side of (41) can be bounded by using the Cauchy-Schwartz and Young's inequalities. This yields:
The second term is bounded by using the inequality as(u, v) < µas(u, u) +as(v, v)/4µ, which holds for all µ > 0 and as(. , .) symmetric positive. Thus,
Finally for the third term we use Lemma 3.2 and Young's inequality to get
Substituting these three inequalities back into (40), we get
Now, the term (β · ∇eh, ηh) may be rewritten as
In order to obtain a bound for ||β · ∇eH||0,T we use the discrete inf-sup condition (A4). Note that
Then, using the Cauchy-Schwartz inequality, the inverse estimate (A3) and Lemmas 3.1 and 3.2, we get
Hence, the term
in (43) is bounded by
Applying Young's inequality to each term gives
Returning now to (42) and (43), and choosing suitable values for µ1, µ2, µ'2, µ3, µ4, µ5 and µ6, we obtain
Next, using the approximation property (A1), the triangular inequality and considering that ε < H, we obtain the estimate (35) given by
Since as(·, ·)|T is L2(T)-coercive, i.e., as(eh, eh)|T>  , we obtain
, we obtain
To obtain the estimate (37) note that
As PH is L2 stable (assumption (A2)), then ||eH||0< c||eh||0. Thus
Now, using again (A1) and (69) we obtain
Finally, considering that
together with assumption (A1), (44) and the relation ε < H, we get the desired result (38).
One may note that the previous estimates recover the same rates of many stabilized methods, like SUPG, and the SGS method as well. Those estimates are also verified by the numerical experiments conducted in the next section.
4 Numerical results
In this section, we provide numerical experiments to evaluate the NSGS convergence rates in the L2 norm and the H1 semi-norm, which are compared to results obtained using the SGS method with  b = cb(measTh) 1/d, cb = 1, unless otherwise indicated. We consider two problems with regular solutions defined in a two-dimensional domain Ω = (0,1) × (0,1), where the medium is assumed homogeneous and isotropic. The structured mesh
b = cb(measTh) 1/d, cb = 1, unless otherwise indicated. We consider two problems with regular solutions defined in a two-dimensional domain Ω = (0,1) × (0,1), where the medium is assumed homogeneous and isotropic. The structured mesh 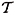 H is formed by connecting the bottom left corner of each mesh square with its top right corner. The convergence of the iterative procedure is obtained when
H is formed by connecting the bottom left corner of each mesh square with its top right corner. The convergence of the iterative procedure is obtained when  < tol = 10-3, where dof stands for the total number of degrees of freedom in
< tol = 10-3, where dof stands for the total number of degrees of freedom in 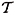 H. In general a small number of iterations is necessary to reach the preset accuracy. We did not consider here computational aspects of both methods since SGS is a linear method and it obviously leads to much cheaper cost. However, the additional computational cost resulting from the NSGS method, or any other stabilized nonlinear method, is surely justified when either the problem is nonlinear or non physical oscillations are not permissible (see e.g. [21] ). One may check the NSGS property of preventing spurious modes through numerical experiments for problems with internal and boundary layers which are reported in [26] .
H. In general a small number of iterations is necessary to reach the preset accuracy. We did not consider here computational aspects of both methods since SGS is a linear method and it obviously leads to much cheaper cost. However, the additional computational cost resulting from the NSGS method, or any other stabilized nonlinear method, is surely justified when either the problem is nonlinear or non physical oscillations are not permissible (see e.g. [21] ). One may check the NSGS property of preventing spurious modes through numerical experiments for problems with internal and boundary layers which are reported in [26] .
4.0.1 Example 1: Advection-diffusion-reaction problem
Consider the problem (1) with β = (1, 0), σ = 1 and ε = 10-3 and 10-7. We also consider the limiting case where ε vanishes. The source term f and Dirichlet boundary conditions are set such that the exact solution is as follows:
The convergence rates are shown in Figures 1-5. The numerical performance of the NSGS method and the SGS method is nearly identical, independently of the diffusion range. Second-order convergence of the error ||u - uh||0 is reached for both methods, and the same happens to ||u - uH||0. Similarly, both methods yield optimal convergence rates for ||∇u - ∇uh||0 and the error ||∇u - ∇uH||0 is also an O(h) as predicted by the analysis. We may also note that the NSGS error of uH decreases more smoothly when compared to the one of uh. Figure also shows that the SGS convergence rates slightly depends on the choice of the free parameter cb.
4.0.2 Example 2: Advection-diffusion problem
We now consider an advection-diffusion problem with β = (1, 0) and the diffusion coefficient equal to 10-3 and 10-6. Homogeneous Dirichlet boundary conditions are prescribed all over the boundary and the source term f is set such that the exact solution is as follows:
The convergence rates are shown in Figures 7 and 9. For ε = 10-3, Figure shows optimal convergence rates (O(h2)) for ||u - uH||0 and nearly optimal for ||u - uh||0, in the case of both NSGS and SGS with cb = 1. Like in the previous test case, optimal convergence rates are reached for both methods in terms of ||∇u - ∇uh||0 and of ||∇u - ∇uH||0 as well. The same behavior occurs for ε = 10-6.
5 Conclusion
In this work we analyzed the Nonlinear Subgrid Method (NSGS) proposedin [25] for advection-diffusion equations. It is based on a two-level approach in which a nonlinear viscosity term is added only to the subgrid scales of the finite element mesh. The amount of subgrid viscosity is scaled by the resolved scale solution at element level, yielding a free parameter method. The discrete setting introduced in [12,13] was used to conduct the analysis. The method was proved to be stable and yields optimal convergence rates by assuming that the grid is quasi-uniform. Under the assumption that the subgrid eddy viscosity is minimum, uniqueness of solution is proved.
Acknowledgments. This research is partially supported by the Brazilian Government, through the Agency CNPq, contracts 304150/2010-0 and 305034/2008-1. We also would like to thank the anonymous referee for the thorough and diligent review which definitely helped to improve the manuscript.
Received: 22/IX/12.
Accepted: 28/IX/12.
#CAM-694/12.
- [1] N.A. Adams, The use of LES subgrid-scale models for shock capturing. Int. J. for Num. Meth. in Fluids, 39 (2002), 783-397.
- [2] F. Brezzi, P. Houston, D. Marini and E. Suli, Modeling subgrid viscosity for advection-diffusion problems. Computer Methods in Applied Mechanics and Engineering, 190 (2000), 1601-1610.
- [3] F. Brezzi and A. Russo, Choosing bubbles for advection-diffusion problems. Math. Models Methods Appl. Sci., 4 (1994), 571-587.
- [4] A.N. Brooks and T.J.R. Hughes, Streamline Upwind Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering, 32 (1982), 199-259.
- [5] M.E. Cawood, V.J. Ervin and W.J. Layton, A nonlinear subgrid-scale model for convection dominated, convection diffusion problems. Technical Report TR2002-12-CEL, Clemson University (2002).
- [6] R. Codina, Analysis of a stabilized finite element approximation of the Oseenequations using orthogonal subscales. Applied Numerical Mathematics, 58(3) (2008), 264-283.
- [7] J. Donea and A. Huerta, Finite Element Methods for Flow Problems. John Wiley & Sons, Chichester (2003).
- [8] Y. Efendiev and T. Hou, Multiscale finite element methods for porous media flows and their applications. Applied Numerical Mathematics, 57(5-7) (2007), 577-596. Special Issue for the International Conference on Scientific Computing.
- [9] L.P. Franca and F. Valentin, On an improved unusual stabilized finite elementmethod for the advective-reactive-diffusive equation. Computer Methods inApplied Mechanics and Engineering, 190 (2000), 1785-1800.
- [10] A.C. Galeăo and E.G. Dutra do Carmo, A Consistent Approximate Upwind Petrov-Galerkin method for convection-dominated problems. Computer Methodsin Applied Mechanics and Engineering, 68 (1988), 83-95.
- [11] V. Gravemeier, The Variational Multiscale Method for Laminar and Turbulent Incompressible Flow. Ph.D. thesis, Institut fur Baustatik der Universitat Stuttgart (2003).
- [12] J.-L. Guermond, Stabilization of Galerkin approximations of transport equation by subgrid modeling. Mathematical Modelling and Numerical Analysis, 33 (1999), 1293-1316.
- [13] J.-L. Guermond, Subgrid stabilization of Galerkin approximations of linear monotone operators. IMA Journal of Numerical Analysis, 21 (2001), 165-197.
- [14] J.-L. Guermond, A. Marra and L. Quartapelle, Subgrid stabilized projection method for 2D unsteady flows at high Reynolds numbers. Computer Methods in Applied Mechanics and Engineering, 195 (2006), 5857-5876.
- [15] G. Hauke and A. García-Olivares, Variational subgrid scale formulations for the advection-diffusion-reaction equation. Computer Methods in Applied Mechanics and Engineering, 190 (2001), 6847-6865.
- [16] N. Heitmann, Subgridscale stabilization of time-dependent convection dominated diffusive transport. J. Math. Anal. Appl., 331 (2007), 38-50.
- [17] T.J.R. Hughes, Multiscale phenomena: Green's functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origin of stabilizedmethods. Computer Methods in Applied Mechanics and Engineering, 127 (1995), 387-401.
- [18] T.J.R. Hughes, L.P. Franca and G.M. Hulbert, A new finite element formulation for computational fluid dynamics: VIII. The Galerkin-Least-Squares method for advective-diffusive equations. Computer Methods in Applied Mechanics andEngineering, 73 (1989), 173-189.
- [19] T.J.R. Hughes, G. Scovazzi and L.P. Franca, Multiscale and Stabilized Methods, Encyclopedia of Computational Mechanics. John Wiley & Sons, Ltd., (2004).
- [20] V. John, S. Kaya and W. Layton, A two-level variational multiscale method for convection-dominated convection-diffusion equations. Computer Methods inApplied Mechanics and Engineering, 195 (2006), 4594-4603.
- [21] V. John and P. Knobloch, On spurious oscillations at layers diminishing (SOLD) methods for convection-diffusion equations: Part II - analysis for P1 and Q1finite elements. Computer Methods in Applied Mechanics and Engineering, 197(21-24) (2008), 1997-2014.
- [22] R. Juanes, Displacement theory and multiscale numerical modeling of three-phase flow in porous media. Ph.D. thesis, Engineering - Civil and Environmental Engineering, University of California, Berkeley (2003).
- [23] L.G. Margolin and W.J. Rider, The design and construction of implicit LESmodels. Int. J. for Num. Meth. in Fluids, 47 (2005), 1173-1179.
- [24] H.G. Roos, M. Stynes and L. Tobiska, Numerical Methods for Singularly Perturbed Differential Equations: Convection Diffusion and Flow Problems. Springer-Verlag, New York (1996).
- [25] I.P. Santos and R.C. Almeida, A nonlinear subgrid method for advection-diffusion problems. Computer Methods in Applied Mechanics and Engineering, 196 (2007), 4771-4778.
- [26] I.P. Santos and R.C. Almeida, A nonlinear subgrid model for transport problems. In Proceedings of the XXVIII Iberian Latin American Congress on Computational Methods in Engineering CILAMCE - Congress on Numerical Methods in Engineering CMNE, Porto, Portugal (2007).
- [27] G. Scovazzi, Multiscale Methods in Science and Engineering. Ph.D. thesis,Mechanical Engineering Department, Stanford University (2004).
- [28] R. Temam, Navier-Stokes Equations, Theory and Numerical Analysis. NorthHolland (1979).
- [29] E. Weinam and B. Engquist, The heterogeneous multiscale methods. Comp. Math. Sci., 1 (2003), 87-132.
- [30] L. Zhang, J. Ouyang and X. Zhang, On a two-level element-free Galerkin method for incompressible fluid flow. Applied Numerical Mathematics, 59(8) (2009),1894-1904.
Publication Dates
-
Publication in this collection
28 Nov 2012 -
Date of issue
2012
History
-
Received
22 Sept 2012 -
Accepted
28 Sept 2012



















































































