Reply on the Comments on When is Statistical Significance not Significant?^*

(SILVA, Glauco P. GUARNIERI, Fernando H. Comments on When is Statistical Significance not Significant? Brazilian Political Science Review. Vol.8, Nº 02, 2014)

It is very rewarding for us to receive a serious commentary on "When is Statistical Significance not Significant?". We are pleased with Silva and Guarnieri's (2014) remarks and we believe that they generally agree with us. However, their review makes it clear that some points were left behind. The principal aim of this paper is to answer Silva and Guarnieri's (2014) comments on

Figueiredo Filho et al. (2013). Methodologically, we use both observational and simulation data to defend our view on the proper use of the p-value statistic in empirical research.

(1) Scholars must always graphically analyze their data before interpreting the p-value

In many cases, as pointed out by Silva and Guarnieri (2014), graphical analysis cannot help you. That being said, ignoring graphs is a much worse path to trail. Graphical analysis is a powerful tool not only for examining linear relationships but also to identify exponential, quadratic, and cubic relationships.

Additionally, graphical analysis can be applied to more descriptive goals not related to the presence of covariates or model selection. We simulated an independent t test comparison between the heights of men and women. For both groups the distribution is normal. Men have an average of 1.75m with a standard deviation of .15. Women have an average of 1.60m with a standard deviation of .10. Figure 1 illustrates the data.

Figure 1
Error bar for the height for men and women without and with outlier (n = 100)

When there is no outlier, as long that there is no overlap between confidence intervals, we may conclude that men are taller than women in the population. The mean difference between groups is statistically significant (p-value<.001). However, in the outlier example we observe an increase in women variance. Therefore, we should be cautious before interpreting the p-value. It is clear that if scholars only evaluate the p-value, they would wrongly conclude that there is no difference between the height of men and women within the population when in fact there is.

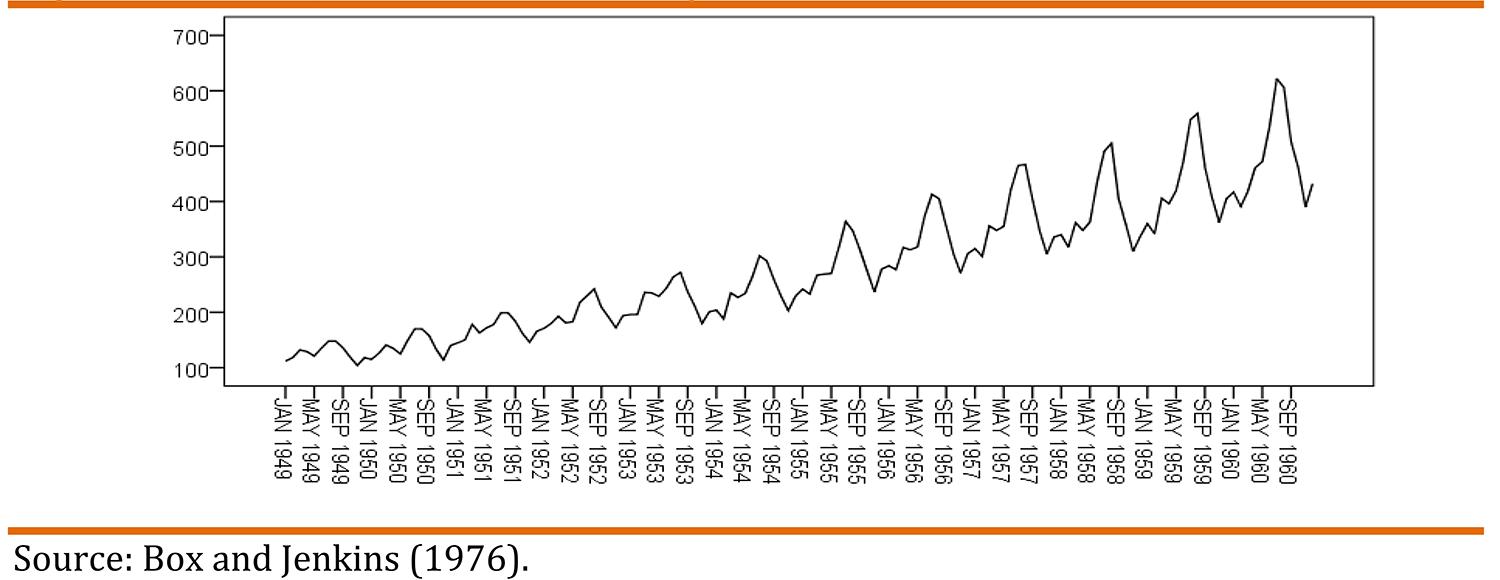
In some specific areas of Statistics, graphs are a fundamental step of the scientific initiative. The selection of the appropriate specification in time series analysis depends heavily on graphs. Let us examine data from Box and Jenkins (1976)^[1].

Figure 2
Monthly total airline passengers from 1949 to 1960

We observe strong seasonality, tendency and increasing variance over time. We must graphically examine the original distribution of the variables before choosing the appropriate model.

Figure 3
Autocorrelations function graph

Using both graphical analysis and adjustment measures, we define the model order that best fits the data. In this case SARIMA (0,1,1) (0,1,1). Graphical analysis is at the heart of all statistical analysis.

Now let us deal directly with Silva and Guarnieri's (2014) example regarding Taagepera's (2012) experiment. They argue that "a simulation of this data shows that the graphical evaluation would not be enough to avoid a misguided analysis" (SILVA AND GUARNIERI, 2014, p, p. 02). We disagree. To make our case we simulated a table of values of y, x₁, x₂ and x₃ following Taagepera (2012). All values are random and the y value came from = 980𝒙₁𝒙₃/𝒙²₂. The next step is to fit a linear model to explain the variance of y and graphically analyze the residuals. Figure 4 displays this information.

Figure 4
How graphs are able to tell that a functional form is not linear

Graphical examination of the standardized residuals and predicted values shows that the relationship is not linear. Graphical analysis reveals that the linear function is not appropriate to model y. We should never adjust regression models without relying on residuals inspection. Silva and Guarnieri (2014) also argue that theory should inform the adequate functional form. We completely agree with them on this. However, sometimes data defies theoretical expectations and at times we do not have strong theoretical assumptions to follow. In the total absence of theoretical guidance, graphical analysis can help scholars in a more inductive pattern.

Finally, modern graphical and statistical tools are very important to data analysis and there is no point in avoiding them. Theory and statistical tools should be applied together in order to advance scientific knowledge. We are not arguing that graphical analysis is helpful at all times. Graphs can be tricky, but ignoring them is way more dangerous.

(2) It is pointless to estimate the p-value for non-random samples

Silva and Guarnieri (2014) argue that the p-value is a measure to adjust a model to our data (SILVA AND GUARNIERI, 2014, p. 03). We disagree. Examples of model adjustment statistics are: r², adjusted r², pseudo r², log likelihood, etc. The p-value is the probability of encountering the observed value of the test-statistic or more extreme departure from the null hypothesis when the null hypothesis is true (EVERITT and SKRONDAL, 2010).

The main problem in estimating p-values for non-random samples is the tendency to overestimate/underestimate the t statistic. In order to show this we simulated a population with 1,000 observations, mean of 59 years (Enivaldo's age) and standard deviation of 16 years (Dalson's age divided by 2). We then selected an ascendant ordered sample of the first 30 cases. Finally, we selected a simple random sample with the same size and compared the samples mean with the population mean. The table 1 summarizes the mean comparison.

Table 1
Simulation (test value = 59)

	N	mean	standard deviation	t	p-value
Population	1,000	59.27	15.39	.547	.584
Simple random sample	30	61.72	15.85	.941	.355
Ascendant ordered sample	30	24.71	5.48	-	.000

• Source: Banco_Dados_Figueiredo et al.

When the sample is random with only 30 observations we get pretty close to the population parameter (59). So close that we cannot reject the null hypothesis (p-value = .355). We also observe that the p-value estimated from the population distribution leads us to not reject H₀ (p-value = .584). This example also illustrates why we should avoid interpreting the p-value when dealing with population data. Finally, when we examine the ascendant ordered sample, the p-value leads us to reject H₀ when we should not (p-value<.001). For the non-random sample we underestimate both the true mean and the standard deviation. The interpretation of the p-value is not reliable for non-random samples.

In short, as long as we are interested in making reliable inferences about reality we must follow the standard procedures of statistical inference. The central limit theorem only applies to random samples. If your sample is not random then you cannot invoke the central limit theorem and therefore both p-values and confidence intervals will be troubled.

(3) The p-value is highly affected by the sample size

Silva and Guarnieri (2014) argues that "the larger the sample size, the higher the p-value" (SILVA and GUARNIERI, 2014, pp. 03-04). The p-value is highly affected by the sample size since the number of cases goes into the denominator. However, the larger the sample size, the lower the p-value goes, and not higher as pointed out by our reviewers. To show the impact of sample size on statistical significance we simulated a random variable with a mean of 128 and a standard deviation of 24. We then tested if the mean differs from 132, varying the sample size from 10 to 300. Figure 5 summarizes this information.

Figure 5
Sample size and p-value

For sample sizes from 10 to 50 the erroneous conclusion would be the same: there is no statistically difference between the sample mean and the population mean. However, as long the sample size reaches 100 cases, the t test is statistically significant at 10% level. When we reach 200 cases, the difference is significant at 1% level. Therefore, the researcher would rightly conclude that the two means are different. Graphical analysis also indicates a negative relationship between sample size and the p-value (r² linear = .632; p-value < .05; n = 7; r² exponential = .985; p-value < .001).

Statistical theory teaches us that estimates from small samples are much more unstable. In addition, when the sample is small, only large effects could reach statistical significance. One of the assumptions of the p-value is that the sample follows a normal distribution. When the sample is small it becomes impossible to reliably test this assumption. Therefore, when the sample is too large even trivial effects can reach statistical significance.

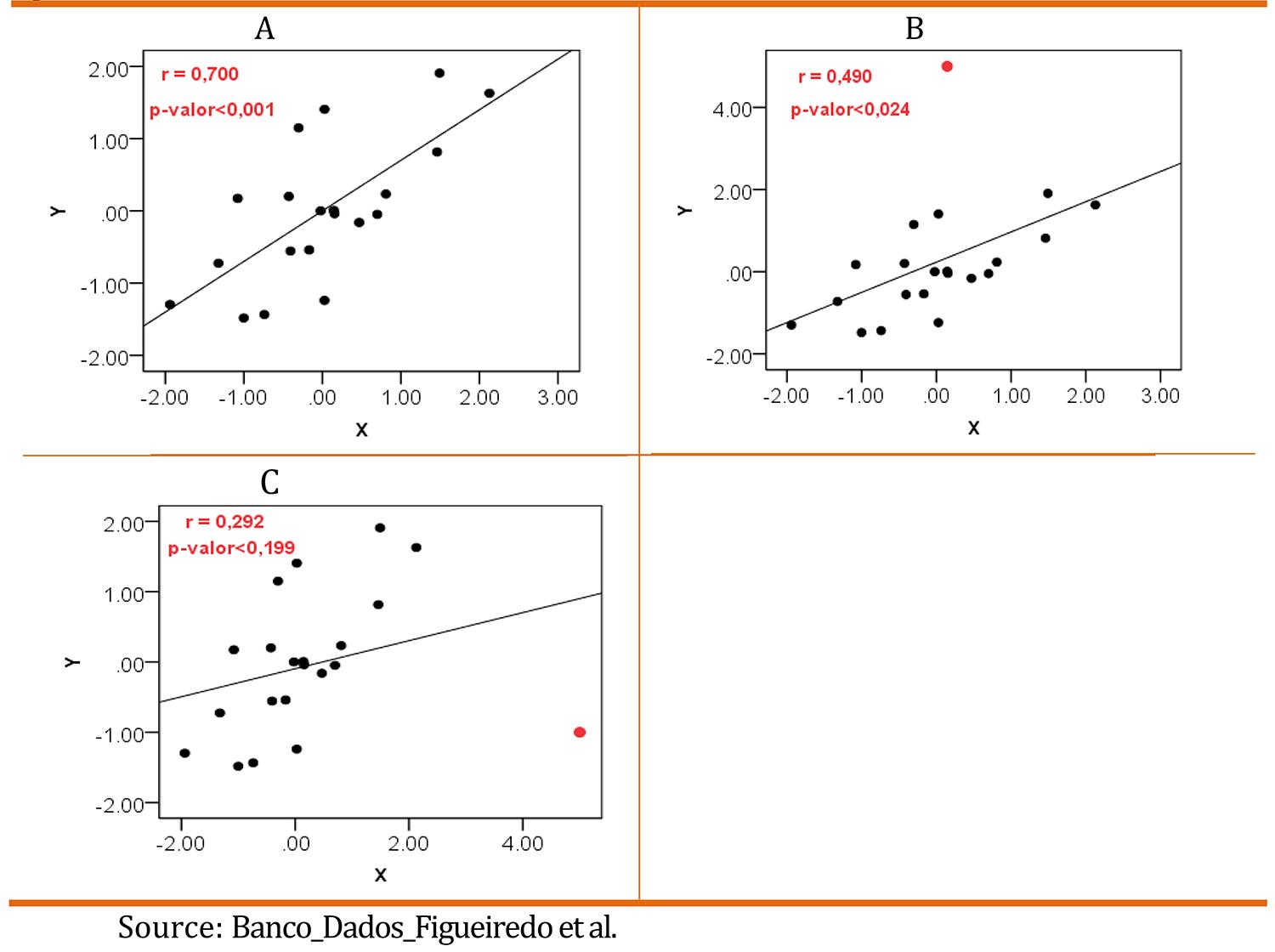
Another problem associated with the interpretation of the p-value in small samples is the outliers, since estimates from small samples are much more affected by deviant cases. To make our case, we simulated two variables with a positive correlation of .7 in a sample of 20 cases. Figure 6 displays this data.

Figure 6
Simulated correlation between X and Y

When the sample size is small, the presence of a single outlier is shattering. The y outlier underestimates the true level of association between X and Y (see figure b). The x outlier affects both the magnitude and the statistical significance of the correlation (see figure c). The conclusion would be that the variables are statistically independent when in fact they are positively correlated. And what happens when the sample size gets bigger? Figure 7 answer this question.

Figure 7
Simulated correlation X and Y

Although we observe an underestimation of the true population parameter (.700), the sample size is enough to reduce the effect of the outlier. There is no substantive change in the conclusions. In short, the interpretation of the value depends on the sample size. The bigger the sample, the lower the p-value. Extremely large samples will reach statistical significant differences/effects regardless of their practical importance.

(4) It is pointless to estimate the p-value when dealing with data on population

We firmly believe that measurement error is not a sufficient reason to estimate p-values when dealing with data from population. Instead, if we were working with a random sample there are some applications of models that specifically deal with measurement error and treats all independent variables as random variables. We believe that p-values cannot reflect the variables measurement quality. The majority of Political Science research is based on samples. However, we are not interested in the sample per se. We are interested in samples insofar as they can help us understand the population. This is the logic behind all statistical inference. The main implication of using samples to learn about population is that we always have some degree of uncertainty. If you are working with the population there is no uncertainty. Therefore, there is no need to estimate the p-value.

General considerations

According to Greenland and Poole (2013) p-values are here to stay. Therefore, it is important to get their interpretation right. Statistical inference depends upon working with a random sample selected from a specific population. Non-random samples tend to produce biased inferences. Scholars from different areas must abandon hypothesis testing based on population. The great advantage of statistics is to estimate the quantity of unknown information (population) based on what we know (sample) with parsimony, low cost, low time and, evidently, with some uncertainty. On the other hand, if you already know all the elements of your population there is no unknown information to be estimated. There is no estimation in the population. We truly appreciate Silva and Guarnieri's (2014) comments. We believe that science is a collective enterprise that can only thrive through the efforts of its members. With this reply we hope to advance the debate on statistical significance in Political Science.

Revised by Paulo Scarpa

References

• BOX, G. E. P.; JENKINS, G. M. (1976). Time series analysis forecasting and control San Francisco: Holden-Say.
• EVERITT, B. S. and SKRONDAL, A. (2010), The Cambridge dictionary of statistics, Cambridge University Press.
• FIGUEIREDO FILHO, D. B.; PARANHOS, R.; ROCHA, E. C. da; SILVA, M. B.; SILVA JUNIOR, J. A.; SANTOS, M. L. and MARINO, J. G. (2013), “When is statistical significance is not significant?”. Brazilian Political Science Review, Vol. 07, pp. 31-55.
• GREENLAND, S. and POOLE, C. (2013), Living with p values: resurrecting a Bayesian perspective on frequentist statistics. Epidemiology. Vol. 24, Nº 01, pp. 62-68.
• SILVA, G. and GUARNIERI, F. (2014), Comments on When is Statistical Significance not Significant. Brazilian Political Science Review Vol. 08, Nº 02, pp. 129-132.
• TAAGEPERA, R. (2012), Logical Models and Basic Numeracy in Social Sciences, in http://www.psych.ut.ee/stk/Begginers_Logical_Models.pdf
  » http://www.psych.ut.ee/stk/Begginers_Logical_Models.pdf

• 1
  Data available at http://calcnet.mth.cmich.edu/org/spss/Prj_airlinePassengers.htm
• [*]
  http://dx.doi.org/10.1590/1981-38212014000100024 The replication dataset can be found in bpsr.org.br/files/arquivos/Banco_Dados_Figueiredo et al.html. We are grateful for the Berkeley Initiative for Transparency in Social Science (BITSS) and thankful to Anderson Silva, Gauss Cordeiro, Ernani Carvalho and Marcelo Medeiros. All limitations are the author's monopoly.

Publication Dates

• Publication in this collection
  Dec 2014