Abstracts
The objective of the current study was to formulate mucoadhesive controlled release matrix tablets of flurbiprofen and to optimize its drug release profile and bioadhesion using response surface methodology. Tablets were prepared via a direct compression technique and evaluated for in vitro dissolution parameters and bioadhesive strength. A central composite design for two factors at five levels each was employed for the study. Carbopol 934 and sodium carboxymethylcellulose were taken as independent variables. Fourier transform infrared (FTIR) spectroscopy studies were performed to observe the stability of the drug during direct compression and to check for a drug-polymer interaction. Various kinetic models were applied to evaluate drug release from the polymers. Contour and response surface plots were also drawn to portray the relationship between the independent and response variables. Mucoadhesive tablets of flurbiprofen exhibited non-Fickian drug release kinetics extending towards zero-order, with some formulations (F3, F8, and F9) reaching super case II transport, as the value of the release rate exponent (n) varied between 0.584 and 1.104. Polynomial mathematical models, generated for various response variables, were found to be statistically significant (P<0.05). The study also helped to find the drug's optimum formulation with excellent bioadhesive strength. Suitable combinations of two polymers provided adequate release profile, while carbopol 934 produced more bioadhesion.
Flurbifrofen/mucoadhesive controlled release tablets/formulation; Flurbifrofen/mucoadhesive controlled release tablets/in vitro evaluation; Drugs/release profile; Drugs/bioadhesion; Tablets/direct compression
O objetivo do presente estudo foi formular comprimidos mucoadesivos de flurbiprofeno, de liberação controlada, e otimizar o perfil da liberação do fármaco e a bioadesão, utilizando a metodologia de superfície de resposta. Prepararam-se os comprimidos via técnica de compressão direta, que foram avaliados in vitro quanto aos parâmetros de dissolução e da força bioadesiva. Planejamento com componente central para dois fatores em cinco níveis cada foi empregado para esse estudo. Carbopol 934 e carboximetilcelulose sódica foram tomados como variáveis independentes. Efetuaram-se estudos de espectroscopia por transformada de Fourier (FTIR) para observar a estabilidade do fármaco durante a compressão direta e para avaliar a interação a fármaco-polímero. Aplicaram-se vários métodos cinéticos para avaliar a liberação do fármaco dos polímeros. Gráficos de superfície de contorno e de resposta foram efetuados para retratar a relação entre as variáveis dependentes e a resposta. Os comprimidos mucoadesivos de flurbiprofeno apresentaram cinética de liberação não-fickiana, estendendo para ordem zero, para algumas formulações (F3, F8 e F9), alcançando transporte super caso II, à medida que o valor do expoente (n) de taxa de liberação variou entre 0,584 e 1,104. Modelos matemáticos polinomiais, gerados por diversas variáveis de resposta, foram estatisticamente, significativos (P<0,05). O estudo também auxiliou a encontrar a formulação ótima do fármaco, com excelente força de bioadesão. Combinações adequadas dos dois polímeros resultaram em perfis de liberação adequado, sendo que o Carbopol 934 produziu mais adesão.
Flurbifrofeno/comprimidos mucoadesivos de liberação controlada/formulação; Flurbifrofeno/comprimidos mucoadesivos de liberação controlada/avaliação in vitro ; Fármacos/perfil de liberação; Fármacos/bioadesão; Comprimidos/compressão direta
INTRODUCTION
Oral controlled release systems continue to be the most popular of all the drug delivery systems available, despite the advancements made in other drug delivery systems (Ponchel, Irache, 1998PONCHEL, G.; IRACHE, J.M. Specific and non-specific bioadhesive particulate systems for oral delivery to the gastrointestinal tract. Adv. Drug. Deliv. Rev., v.34, p.191-219, 1998.). Conventional oral dosage forms often produce fluctuations in drug plasma levels that either exceed safe therapeutic levels or quickly fall below the minimum effective levels; this effect is usually entirely dependent upon the particular agent's biologic half-life, frequency of administration, and its release rate (Theeuwes et al., 1983THEEUWES, F. OROS Osmotic system development. Drug. Dev. Ind. Pharm., v.7, p.1331-1357, 1983.).
Mucoadhesive delivery systems offer many advantages over other oral controlled release systems; they prolong the residence time of the drug in the gastrointestinal tract and they target and localize the dosage form at a specific site (Lavelle, 2001LAVELLE, E.C. Targeted delivery of drugs to the gastrointestinal tract. Crit. Rev. Ther. Drug Carrier. Syst., v.18, p.341-386, 2001.; Hou, Cowles, Berner, 2003HOU, S.Y.; COWLES, V.E.; BERNER, B. Gastric retentive dosage forms: a review. Crit. Rev. Ther. Drug Carrier. Syst., v.20, p.459-497, 2003.). Mucoadhesive formulations are known to provide close contact between the dosage form and the mucus membrane, resulting in high drug flux through the absorbing tissue (Woodley, 2001WOODLEY, J. Bioadhesion: new possibilities for drug administration? Clin. Pharmacokinet., v.40, p.77-84 2001.; Singh, Chakkal, Ahuja, 2006SINGH, B.; CHAKKAL, S.K.; AHUJA, N. Formulation and optimization of controlled release mucoadhesive tablets of atenolol using response surface methodology. AAPS PharmSciTech., v.7, p.e3, 2006.).
Inflammatory processes cause many oral cavity diseases, which can be treated with flurbiprofen, a potent anti-inflammatory, analgesic, and antipyretic agent belonging to the family of propionates. Its shorter half-life (2-6 hours) limits its extensive use when compared to many of the newer agents, possibly because it requires around-the-clock administration and has harmful gastric side effects (Dollery, 1991DOLLERY, C. (Ed.). Therapeutic drugs. New York: Churchill Livingstone, 1991. p.297-299.). Flurbiprofen, when administered as conventional tablets, has been reported to exhibit fluctuations in plasma drug levels, which can result in either the manifestation of side effects or in the reduction of drug levels at the receptor site (Vaithiyalingam et al.,2001VAITHIYALINGAM, S.R.; SASTRY, S.V.; DEHON, R.H.; REDDY, I.K.; KHAN, M.A. Long-term stability characterization of a controlled release gastrointestinal therapeutic system coated with cellulose acetate pseudolatex. Pharmazie, v.56, p.66-69, 2001.). Thus, a mucoadhesive controlled release tablet of flurbiprofen, which maintains plasma concentrations effectively over a 24-hour period, and which has the ability to avoid gastric-related adverse effects will heighten its area of application.
In the development of the mucoadhesive controlled release dosage form, an important issue to address was to design an optimized formulation using a minimum number of experiments within a short amount of time. For this reason, a computer optimization technique, based on response surface methodology (RSM) utilizing a polynomial equation has been widely used. RSM is a collection of statistical and mathematical techniques that has been successfully used to determine the effects of several variables while optimizing processes (Atkinson, Donev, 1992ATKINSON, A.C.; DONEV, A.N. Optimum experimental designs. Oxford: Oxford University Press, 1992. p. 132-189.). RSM is an extensively practiced approach in the development and optimization of drug delivery devices (Dave et al., 2004DAVE, B.S.; AMIN, A.F.; PATEL, M.M. Gastroretentive drug delivery system of ranitidine hydrochloride: formulation and in vitro evaluation. AAPS PharmSciTech., v.5, p.e34, 2004.; Singh et al.,2005aSINGH, B.; KUMAR, R.; AHUJA, N. Optimizing drug delivery systems using systematic "design of experiments". Part I: Fundamental aspects. Crit. Rev. Ther. Drug Carrier. Syst., v.22, p.27-105, 2005a.; Singh et al., 2005bSINGH, B.; DAHIYA, M.; SAHARAN, V.; AHUJA, N. Optimizing drug delivery systems using systematic "design of experiments". Part II: Retrospect and prospects. Crit. Rev. Ther Drug Carrier. Syst., v.22, p.215-294, 2005b. ). The technique requires minimal experimentation and time, thus proving to be less laborious and time-consuming, but it is also more cost-effective than other approaches that are required for the optimization of a process. The different types of RSM designs available may include central composite design (CCD), three-level factorial design, Box-Behnken design, and D-optimal design (Box, Wilson, 1951BOX, G.E.P.; WILSON, K.B. On the experimental attainment of multifactorial conditions. J. Roy. Statist. Soc., v.13, p.1-45, 1951.). In the present study, CCD is employed to fit a second-order polynomial by a least squares technique. An equation is also used to describe how the test variables affect the response and determine the interrelationship among the variables.
The aim of this study was to develop and optimize an oral mucoadhesive controlled release tablet of flurbiprofen using RSM, as it may prove to be more fruitful than the conventional controlled release systems by virtue of prolongation of the drug residence time in the gastrointestinal tract. The computer-aided optimization technique using a CCD was employed to study the effect of two independent variables (factors) (i.e., the amounts of two mucoadhesive swellable polymers) on drug release profiles and bioadhesive strength.
MATERIALS AND METHODS
Materials
The materials used in the study include flurbiprofen, which was donated by Hamaz Pharmaceuticals (Pvt.) Ltd. Multan, Pakistan. High-viscosity grade carbopol 934 (CP) and sodium carboxymethylcellulose (SCMC) were donated by Friends Pharmaceuticals (Pvt.) Ltd., Lahore, Pakistan. Gastric mucosa of rabbit was obtained from the rabbit at the university animal house. Analytical grade potassium dihydrogen phosphate, sodium hydroxide, magnesium stearate, lactose, and other chemicals were purchased from E. Merck Co, Darmstadt, Germany.
Formulation of mucoadhesive compressed matrix tablets
Table I shows varying amounts of polymers (i.e., CP and SCMC), along with the diluents (lactose) and calculated amount of lubricant (1% w/w magnesium stearate). The drug and all of the excipients, except for the lubricant, were homogeneously blended in a plastic bag for 15 minutes, followed by further blending of 5 minutes after the addition of the lubricant. The blend was then directly compressed into flat-faced tablets (500 mg) at a constant compression load using a single-punch tablet machine (Emmy, Pakistan).
Experimental design
A CCD with α = 1.414 was employed as per the standard protocol (Shah et al., 2009SHAH, S.N.H.; ASGHAR, S.; CHAUDHARY, M.A.; AKASH, M.S.; REHMAN, N.; BAKSH, S. Formulation and evaluation of natural gum-based sustained release matrix tablets of flurbiprofen using response surface methodology. Drug. Dev. Ind. Pharm., v.35, p.1470-1478, 2009.; Singh et al., 2005cSINGH, B.; MEHTA, G.; KUMAR, R.; BHATIA, A.; AHUJA, N.; KATARE, O.P. Design, development and optimization of nimesulide-loaded liposomal systems for topical application. Curr. Drug Deliv., v.2, p.143-153, 2005c.). The amounts of CP (X1) and SCMC (X2) were selected as the factors, which were studied at five levels each. The central point (0,0) was studied in quintuplicate. All other formulation and processing variables were kept invariant throughout the study. Tables II and III summarize an account of the 13 experimental runs studied, their factor combinations, and their translation of coded levels to the experimental units employed during the study. The percent release at 4 hours (rel4h), the percent release at 12 hours (rel12h), and bioadhesive strength f were taken as the response variables.
Evaluation of tablets
Physical evaluation of tablets
Tablets were evaluated for weight variation (n=20), hardness (n=10), thickness (n=10), and friability (n=10).
Fourier transform infrared spectroscopy
Fourier transform infrared (FTIR) spectroscopy using attenuated total reflectance (ATR) technology for active drug, tablet before, and tablet after compression were taken using Bruker FTIR (Tensor 27 series; Bruker Corporation, Billerica, USA), and OPUS data collection software (Bruker Corporation) was used to evaluate the interaction between the drug and the polymers in the matrix tablets before and after compression. Small amounts of powdered samples were directly placed onto the pike miracle ATR cell in such a way that the sample covered the ZnSe crystal surface, and the arm of the assembly was rotated so that a compact sample mass was formed onto the cell and scanned over a range of 4000 cm-1 to 400 cm-1. Before taking the spectrum of any sample, a blank background scan was performed with an empty cell plate. The procedure described above was then repeated after placing the sample to be analyzed onto the pike miracle ATR cell.
In vitro drug release studies
Automatic USP dissolution apparatus-II (paddle method), attached with an auto-sampler (Watson Marlo, Stockholm, Sweden) was used to determine the drug release profile of all mucoadhesive matrix tablets in triplicate. Six tablets from each formulation were subjected to dissolution studies. Phosphate buffer maintained at a pH of 6.8 in a volume of 900 mL was selected as the dissolution medium and maintained at 37 °C (±0.5 °C). The paddle was rotated with a rotation speed of 50 rpm. Then, 10 μm sintered filters (Pharma Test, Hainburg, Germany) were used to filter aliquots of about 5 mL, withdrawn at 0, 0.5, 1.0, 1.5, 2.0, 4.0, 8.0, 12.0, 16.0, 20.0, and 24.0 hours via auto-sampler. Collected samples were analyzed at 247 nm using a spectrophotometer, and drug release profiles were evaluated by drawing them in Microsoft Excel software (Microsoft Corporation, Redmond, WA, USA).
Measurement of ex vivo bioadhesive strength
Bioadhesive strength of mucoadhesive tablets, measured as the force of detachment against rabbit gastric mucosa, was determined using a modification of the weighing assembly. The rabbit's mucosal membrane was made clear from underlying connective and adipose tissue and then excised and equilibrated at 37 °C±1 °C in phosphate buffer for 30 minutes. Mucoadhesive tablets from each batch, under a constant weight of 5 g, were then placed onto the mucosal membrane for 1 minute. The force required to detach the mucoadhesive tablet from the mucosa was regarded as the bioadhesive strength, and it was measured in terms of weight in grams.
Release modeling
Drug release kinetics are assumed to reflect the different release mechanisms of controlled release matrix systems. Therefore, four kinetic models were applied to analyze the drug release data to find the best fitting equation (Philip, Pathak, 2006PHILIP, A.K.; PATHAK, K. Osmotic flow through asymmetric membrane: A mean for controlled delivery of drugs with varying solubility. AAPS PharmSciTech., v.7, p.E1-E11, 2006.). These models are zero-order, first-order, Higuchi, and Korsmeyer-Peppas, as given in Equations 1-4:
Qt = k0 t (1)
logQ t = log Q 0 k 1 t (2)
Qt = kH t1/2 (3)
where: Q t is the amount of drug released at time t; Q 0 is the initial amount of the drug in the formulation,k 0, k 1, k H, and k KP are the release rate constants for zero-order, first-order, Higuchi model, and Korsmeyer-Peppas models, respectively. In Equation 4, M t and M ∞ are the amount of drug released at time t and ∞, while n is the diffusion coefficient.
Optimization of statistical data analysis
Multiple linear regression analysis (MLRA) was performed using Design Expert software(r) (Design Expert trial version 7.0.0; Stat-Ease, Inc., Minneapolis, MN, USA). A second-order polynomial model was then constructed using the results, including interaction and quadratic terms, along with linear terms. In general, the MLRA model can be represented as follows:
Y = β0 + β1X1 + β2X2 + β11X12 + β22X22 + β12X1X2 (5)
where: Y is the selected response; β 0 is the intercept representing the arithmetic mean of all experimental runs performed; β 1 and β 2 are the coefficients of the linear terms; β 11 and β 22 are the coefficients of the quadratic terms; β 12 is the coefficient of the interaction terms calculated by the observed experimental response values of Y, X 1 and X 2 are the coded levels of independent variables; X 1 2 and X 2 2 are the quadratic terms, and X 1 X 2 is the interaction term.
Design expert software was also used to evaluate statistical validity of the constructed polynomial models by performing one-way analysis of variance (ANOVA). Two-dimensional contour and three-dimensional surface plots were also drawn for each response variable, depending on the respective polynomial model. These plots served as a very good tool for analyzing the interaction effects of the studied dependent variables (Shah et al.,2009SHAH, S.N.H.; ASGHAR, S.; CHAUDHARY, M.A.; AKASH, M.S.; REHMAN, N.; BAKSH, S. Formulation and evaluation of natural gum-based sustained release matrix tablets of flurbiprofen using response surface methodology. Drug. Dev. Ind. Pharm., v.35, p.1470-1478, 2009.; Mandal et al., 2007MANDAL, U.; GOWDA, V.; GHOSH, A.; SELVAN, S.; SOLOMAN, S.; PAL, T.K. Formulation and optimization of sustained release matrix tablet of metformin HCl 500 mg using response surface methodology. Yakugaku. Zasshi., v.127, p.1281-1290, 2007.).
RESULTS AND DISCUSSION
Physical evaluation of tablets
The results for the physical evaluation of the tablets showed that all batches of tablets were within the limits of the United States Pharmacopeia. Tablet weights varied between 498.52 mg and 501.79 mg (mean: 500.43 mg), hardness between 12.39 kg cm-2 and 19.1 kg cm−2 (mean: 14.34 kg cm−2), thickness between 4.37 mm and 4.63 mm (mean: 4.56 mm), and friability ranged between 0.22% and 0.64% (mean: 0.46%).
Fourier transform infrared spectroscopy
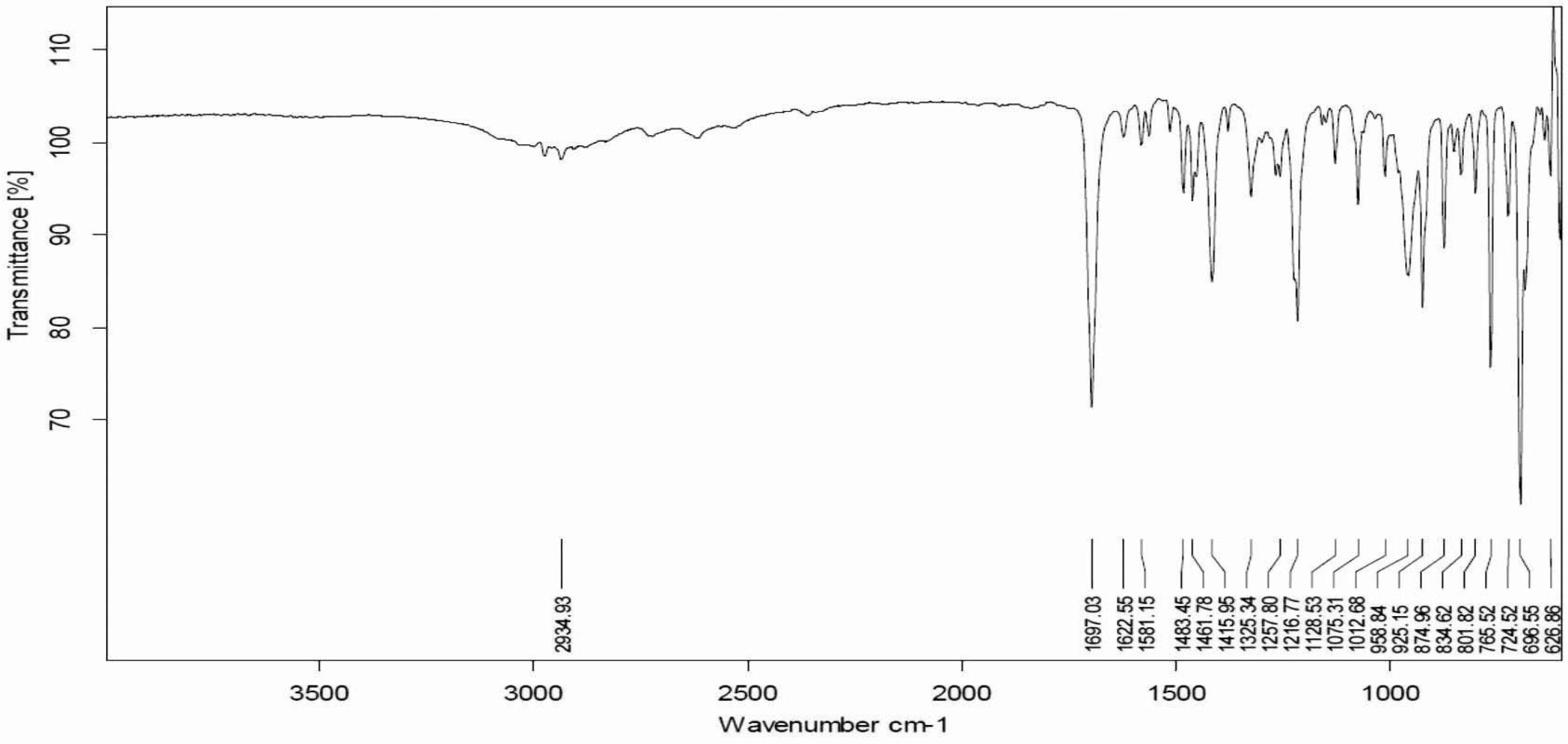
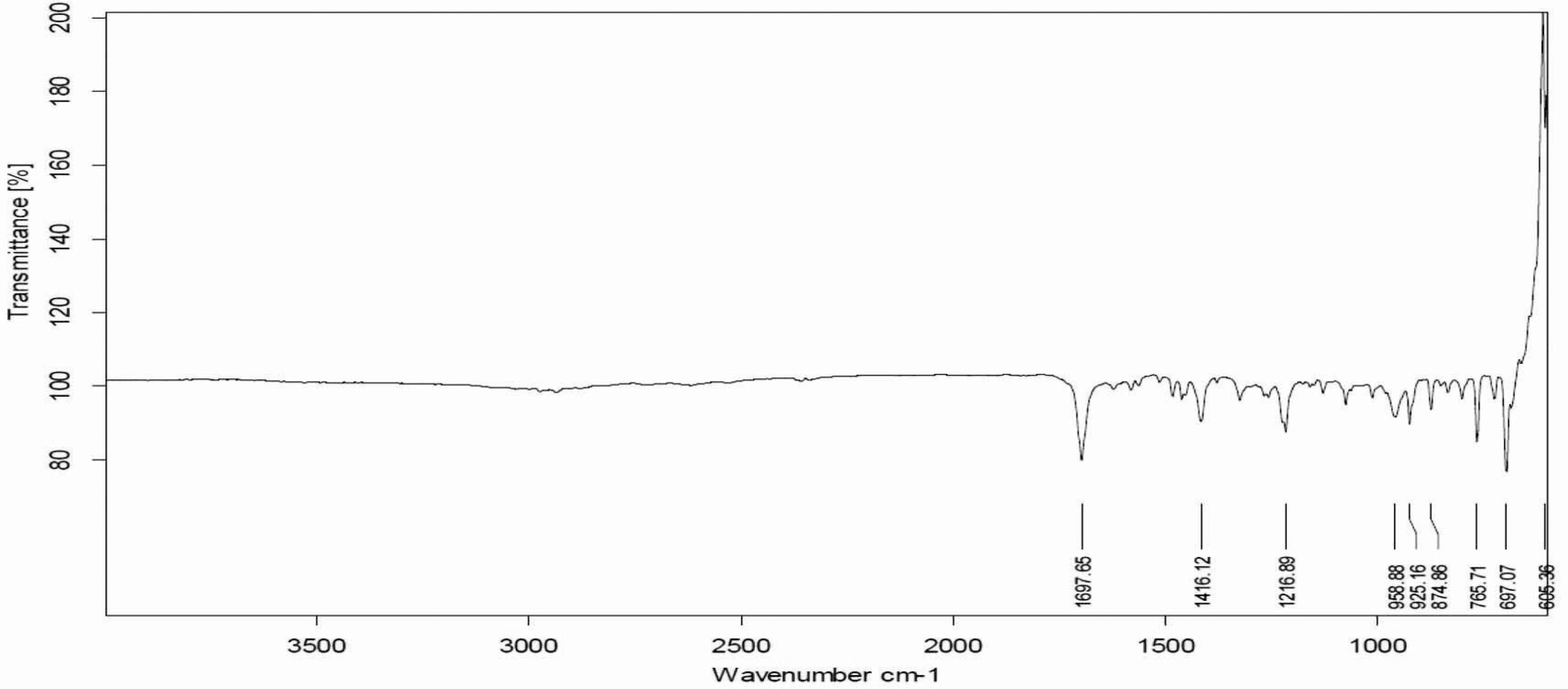
FTIR spectra of pure flurbiprofen (Figure 1) and mucoadhesive controlled release powder mixture before compression (Figure 2) and after compression (Figure 3) did not show any change in the identified peaks. The main peak of the drug remained unaffected after compression, which indicates the stability of drug. Therefore, it was concluded that applied compression force has no effect on drug stability, and no polymer interaction and deformation was observed during the entire course of tablet preparation. FTIR spectra of flurbiprofen showed characteristic broad peaks of the drug in the range of 3500 cm−1 to 2500 cm−1 because of hydrogen bonding. Conversely, the characteristic peaks of the drug at 1697 cm−1 and 2935 cm−1were indicative of carbonyl and hydroxyl stretching, respectively. These FTIR studies are found to be in line with previous studies, suggesting that there was drug stability during the direct compression technique (Shah et al., 2009SHAH, S.N.H.; ASGHAR, S.; CHAUDHARY, M.A.; AKASH, M.S.; REHMAN, N.; BAKSH, S. Formulation and evaluation of natural gum-based sustained release matrix tablets of flurbiprofen using response surface methodology. Drug. Dev. Ind. Pharm., v.35, p.1470-1478, 2009.).
In vitro drug release studies
Table IV lists various kinetic models computed for all the controlled release mucoadhesive formulations. Flurbiprofen release data was evaluated by zero-order, first-order, and Higuchi models. It is depicted in the tables that some formulations follow zero-order patterns for the release of the drug, with an observed general trend of more linearity in the regression line for formulations that have almost double the concentration of either polymer, such as F3, F6, F7, and F9. Most of the formulations follow first-order release patterns because the plots of the percent cumulative drug release versus the square root of time were found to be linear, with regression coefficient (R 2) values ranging from 0.9289 to 0.9864 for the nine formulations. Hence, the mechanism of drug release from the matrices was found to be diffusion-controlled. The Higuchi model failed to explain the release mechanism because the dissolution of the controlled release matrix tablets followed the anomalous release behavior (a combination of diffusion and erosion). Hence, the release data were subjected to the Korsmeyer-Peppas equation, which is used to describe anomalous release behavior from the matrix tablets. In the present study, the values of n, calculated per the algorithm proposed by Peppas and Sahlin (1989)PEPPAS, N.A.; SAHLIN, J.J. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. Int. J. Pharm., v.57, p.169-172, 1989., ranged between 0.5840 and 1.1040. Generally, the release pattern was found to be non-Fickian, as it tended to approach zero-order, while some formulations reached super case II transport, especially when high levels of both polymers were combined. The values of the kinetic constant (kkp), which is a direct function of matrix solubility, were found to decline with increases in the amount of either polymer (Korsmeyer et al., 1983KORSMEYER, R.W.; GURNEY, R.; DOELKER, E.; BURI, P.; PEPPAS, N.A. Mechanisms of solute release from porous hydrophilic polymers. Int. J. Pharm., v.15, p.25-35, 1983.; Korsmeyer et al., 1983aKORSMEYER, R.W.; GURNY, R.; DOELKER, E.; BURI, P.; PEPPAS, N.A. Mechanisms of potassium chloride release from compressed, hydrophilic polymeric matrices: effect of entrapped air. J. Pharm. Sci., v.72, p.1189-1191, 1983a.). It should be noted that k1 has much lower values when compared to k0, clearly indicating that the release of the drug was primarily controlled by Fickian diffusion, along with the varying contribution of the polymer relaxation (case II transport) mechanism as well. It was observed that swelling and erosion (case II transport) of the tablets go on to increase in association with an increase in the content of any of the polymers.
Dissolution data modeling showing the release kinetics of flurbiprofen controlled release matrix tablets containing CP and SCMC
Table V and Figure 4 show that the values of the drug released at 4 hours (rel4hrs) decreased noticeably from 48.786%, which was observed at low levels of both of the polymers, to as low as 10.032%, which was observed at high levels of both of the polymers. This finding indicated the substantial release-retarding potential of the polymers for flurbiprofen. The initial burst release of the drug was shown by the formulations with lower amounts of polymers, which is due to the dissolution of the drug that is initially present at the surface of the matrices, and due to the presence of higher amounts of unreleased drug present in the specific dosage form (Suryakanta et al., 2011SURYAKANTA, S.; DINDA, S.C.; SARWAR, B.; SRUTI, J.; VIKAS, S.; BHANOJI, R. Design and characterization of oral sustained release mucoadhesive matrix tablets of didanosine. Asian J. Pharm. Sci. Res., v.1, p.38-60, 2011.). Another reason for the initial burst release of the drug is that the dosage forms, in the early dissolution period, primarily exhibit first-order Fickian diffusion mechanisms. Higher amounts of the drug released due to Fickian diffusion (i.e., due to k1), as compared to that released due to polymer relaxation (i.e., due to k2), in the early time periods could also be a cause of initial burst release. The cumulative proportion of the drug released due to the case II relaxational transport constant (k2) increased for all of the formulations in association with increasing dissolution time periods, indicating that the release was significantly influenced by polymer relaxation in the later stages. However, formulations showed little burst effect at higher polymer levels, ratifying better sustenance of drug release (Singh, Chakkal, Ahuja, 2006SINGH, B.; CHAKKAL, S.K.; AHUJA, N. Formulation and optimization of controlled release mucoadhesive tablets of atenolol using response surface methodology. AAPS PharmSciTech., v.7, p.e3, 2006.).
In vitro drug release profile of flurbiprofen from directly compressed mucoadhesive tablets containing CP and SCMC.
Almost 88.912%-99.894% of flurbiprofen is released from all 13 formulations at 24-hour time intervals, which signifies almost complete drug release from all of the formulations. Hence, the overall rate of the drug release data (until 12 hours) was determined (as shown in Table V and Figure 4) via observation based on indiscriminating drug release for all of the formulations until a period of 24 hours. The rate of the drug release (until 12 hours) tended to decrease with increase amounts of either CP or SCMC. According to literature findings, the slowing effect of both polymers is due to increases in the viscosity of the gel layer around the matrix tablet (Ford, Rubinstein, Hogan, 1985FORD, J.L.; RUBINSTEIN, M.H.; HOGAN, J.E. Formulation of sustained release promethazine hydrochloride tablets using hydroxypropyl methyl cellulose matrices. Int. J. Pharm., v.24, p.327-338, 1985.; Vazques et al., 1992VAZQUES, M.J.; PEREZ, M.B.; GOMEZ, J.L.; MARTINEZ, P.R.; SOUTO, C.; CONCHEIRO, A. Influence of technological variables on release of drugs from hydrophilic matrices. Drug Dev. Ind. Pharm., v.18, p.1355-1375, 1992.). Both polymers have a tendency of forming gel when they come into contact with water. So, at high levels, hydrogel concentrations are increased around the tablet, and so is the viscosity of the gel layer, which results in decreases in the effective diffusion coefficient of the drug, which then consequently limits the release of the drug from the matrix (Skoug et al.,1993SKOUG, J.W.; MIKELSONS, M.V.; VIGNERON, C.N.; STEMM, N.L. Qualitative evaluation of the mechanism of release of matrix sustained release dosage forms by measurement of polymer release. J. Control. Release, v.27, p.227-245, 1993.). Gel formation occurs due to dissociation of the carboxyl groups of CP at a pH above their pKa (i.e., 6.0±0.5), which causes uncoiling and the expansion of molecules due to the production of an electrostatic repulsive force between the negatively charged carboxyl groups. Uncoiling and expansion of the molecules result in polymer swelling and, consequently, gel is formed, which consists of closely packed swollen particles. With increases in the amount of polymer, this gelling property increases, and thicker gel restrains water penetration, which ultimately reduces the release of the drug (Singh, Chakkal, Ahuja, 2006SINGH, B.; CHAKKAL, S.K.; AHUJA, N. Formulation and optimization of controlled release mucoadhesive tablets of atenolol using response surface methodology. AAPS PharmSciTech., v.7, p.e3, 2006.; Suryakanta et al., 2011SURYAKANTA, S.; DINDA, S.C.; SARWAR, B.; SRUTI, J.; VIKAS, S.; BHANOJI, R. Design and characterization of oral sustained release mucoadhesive matrix tablets of didanosine. Asian J. Pharm. Sci. Res., v.1, p.38-60, 2011.). At high levels of both polymers, a considerable fraction of the drug (~44%) remained unreleased until 12 hours, which can eventually lead to significant reductions in the extent of bioavailability.
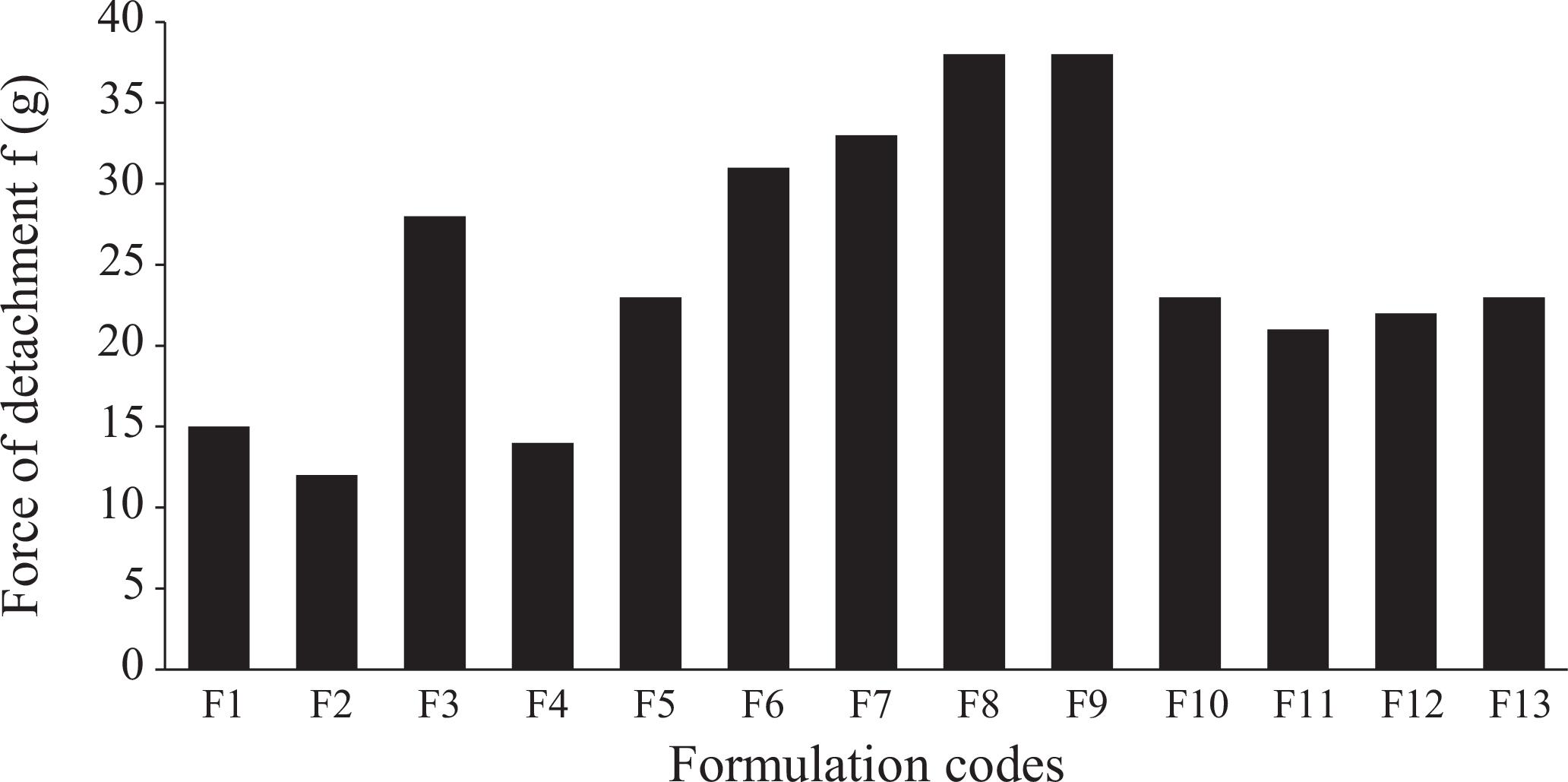
Graphical representation of bioadhesive strengths required for the detachment of mucoadhesive tablets from a rabbit's intestine.
Measurement of ex vivo bioadhesive strength
Bioadhesive strengths of all 13 formulations are presented in Figure 5, which depicts a great variation among the bioadhesive strengths of the formulation. A general trend of increasing bioadhesive strength was observed with increases in either of the polymer's contents, and maximum strength (f) was seen with the highest levels of the two polymers. Formulations showed significant differences in bioadhesive strength and decreases in the order of F9> F8> F7> F6> F3> F5> F1> F4> F2 from 38 g to 12 g. This is in agreement with literature findings that both polymers have a tendency to swell immediately when they come in direct contact with the hydrated mucus membrane (Peppas, Sahlin, 1996PEPPAS, N.A.; SAHLIN, J.J. Hydrogels as mucoadhesive and bioadhesive materials: a review. Biomaterials, v.17, p.1553-1561, 1996.). Uncoiling of polymer chains occurs as a result of water sorption, which is responsible for reductions in glass transition temperatures below room conditions. These uncoiled chains eventually result in subsequent increases in chain mobility. The reduced glass-rubbery transition makes polymers plasticized, which increases the polymer surface area for maximum contact with the mucus membrane and it also increases chain flexibility for interpenetration into the mucus membrane (Duchen, Touchar, Peppas, 1988DUCHEN, D.; TOUCHAR, F.; PEPPAS, N.A. Pharmaceutical and medicinal aspects of bioadhesive systems for drug administration. Drug Dev. Ind. Pharm., v.14, p.283-318, 1988.) There is no citation in the reference part! Please, white it. Therefore, an increase in the amount of polymer results in the provision of a greater surface area and more polymer chains for interpenetration with mucin, resulting in the augmentation of bioadhesive strength (Ponchel et al., 1987PONCHEL, G.; TOUCHARD, F.; DUCHENE, D.; PEPPAS, N.A. Bioadhesive analysis of controlled release systems. I. Fracture and interpenetration analysis in poly (acrylic acid) containing systems. J. Control. Release, v.5, p.129-141, 1987.).
RSM optimization results
CCD, with two factors at five levels, was selected for the study with 13 experimental runs. Table V consists of responses of selected independent variables (X1 and X2) in terms of the percent release at 4 hours (Y1), the percent release at 12 hours (Y2), and force of detachment or bioadhesive strength (Y3) required for the detachment of the tablet from the mucus membrane.
Mathematical modeling
Design Expert software (version 7.0.0) was used to establish mathematical relationships in the form of polynomial equations using MLRA for the studied response variables, as expressed in Equations 6, 7, and 8.
Y1 = 30.54 - 6.07X1 - 6.67X2 -3.41X12 - 3.39X22 + 1.54X1X2 (6)
Y2 = 60.02 - 11.99X1 - 10.10X2 + 3.59X12 + 5.12X22 + 1.29X1X2 (7)
Y3 = 22.20 + 7.94X1 + 5.63X2 + 2.96X12 + 0.96X22 - 2.75X1X2 (8)
Polynomial equations consist of coefficients for the intercept, first-order main effects, interaction terms, and higher-order effects. The relative influence of each factor on overall response can be signified from the sign and magnitude of the main effects, where a positive sign would be considered to have a synergistic (positive) effect, while a negative sign would indicate an antagonistic (negative) effect. Design Expert software was also used to evaluate the statistical validity of the constructed polynomial equations by performing one-way analysis of variance (ANOVA), as shown in Tables VI, VII, and VIII for Y1, Y2, and Y3, respectively. Using a 1.414% significance level, a model is considered significant if the P-value (significance probability value) is less than 0.05 (Shah et al., 2009SHAH, S.N.H.; ASGHAR, S.; CHAUDHARY, M.A.; AKASH, M.S.; REHMAN, N.; BAKSH, S. Formulation and evaluation of natural gum-based sustained release matrix tablets of flurbiprofen using response surface methodology. Drug. Dev. Ind. Pharm., v.35, p.1470-1478, 2009.; Vijayalakshmi et al., 2008VIJAYALAKSHMI, P.; DEVI, V.K.; NARENDRA, C.; SRINAGESH, S. Development of extended zero-order release gliclazide tablets by central composite design. Drug Dev. Ind. Pharm., v.34, p.33-45, 2008.). The slowing effect of both independent variables X 1 (CP) and X 2 (SCMC) is depicted in Equation 6, which shows that both polymers have a negative effect on Y1, with a slightly more negative effect in the case of SCMC, confirming its release rate slowing ability. In Table VI, the value of P is less than 0.05 for linear contributions of X 1 (CP) and X 2 (SCMC); therefore, they are considered to have significant effects on the release of the drug from the controlled release matrix tablets after 4 hours. The quadratic response of CP (X 1 2) and SCMC (X 2 2), being significant, also has a more pronounced slowing effect on the release of the drug.
Polynomial Equation 7 shows the negative effect of both polymers at a 12-hour time interval. It is quite evident from Equation 7 that the slowing effect of the polymers is increased, and that CP has a comparatively greater negative influence, showing more release-retarding ability of CP at 12 hours. Linear responses X 1 (CP) and X 2 (SCMC), in the case of Y2, have P-values of 0.0003 and 0.0009, respectively; therefore, they are also considered significant, but the quadratic response (X 1 2) with a P-value of 0.1107 is not significant, which is represented in Table VII. The cross-product contribution (X 1 X 2) for both of these response variables (Y1 and Y2) are not significant as P-values, for these are greater than 0.05.
Both linear terms, X 1 (CP) and X 2 (SCMC), are very influential as far as bioadhesive strength is concerned (as depicted in Equation 8 and Table VIII). Polynomial Equation 8 shows a more positive effect of CP, confirming the more mucoadhesive property of CP, as compared to SCMC. The P-value, being less than 0.05 for these linear terms, is considered significant. Polynomial Equation 8 also shows the significance of the combined polymer effect on bioadhesion. The P-value for the cross-product contribution (X 1 X 2) is 0.0272, which confirms the significance of the combined effect of both polymers on bioadhesion.
Response surface analysis
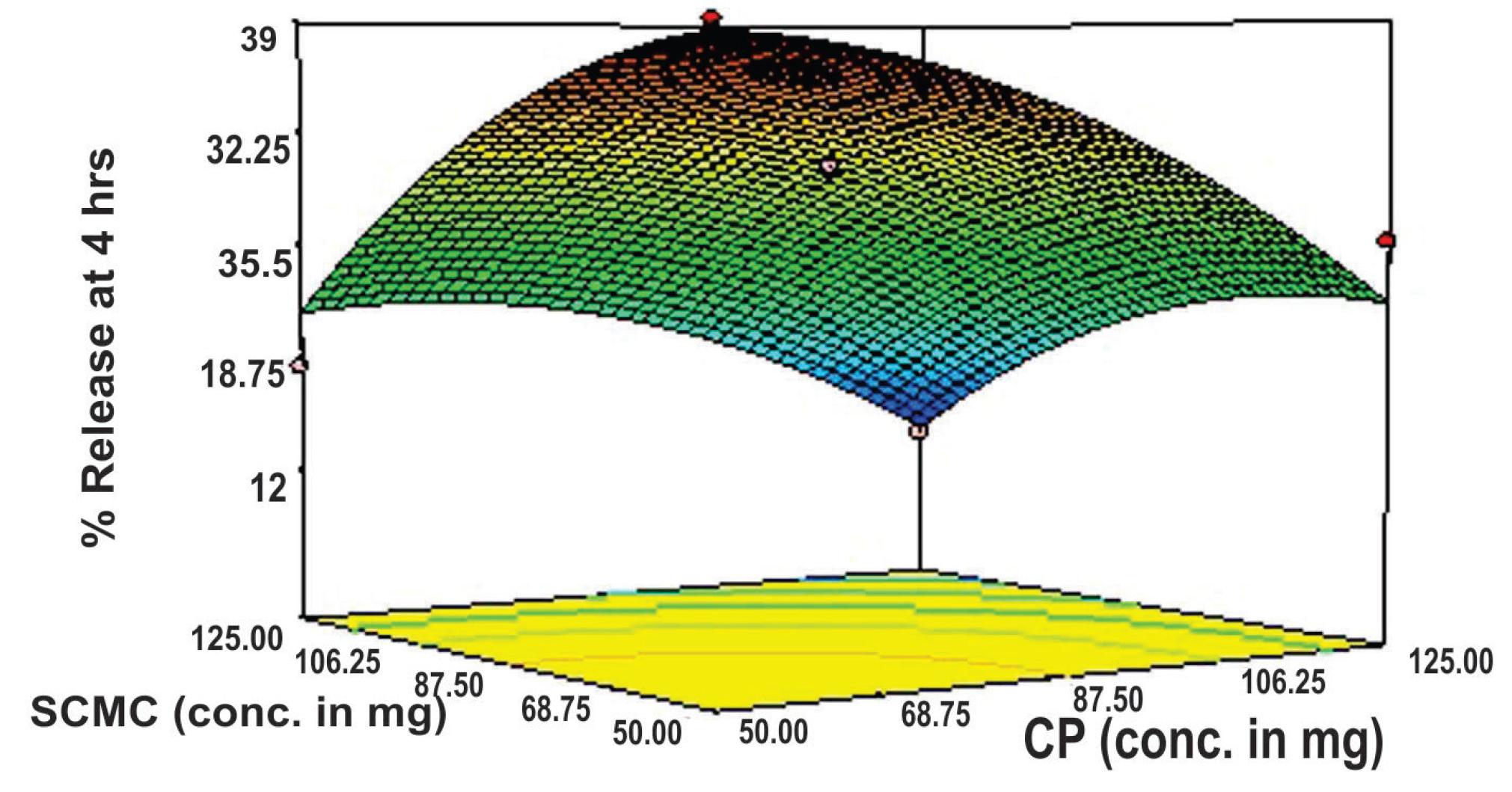
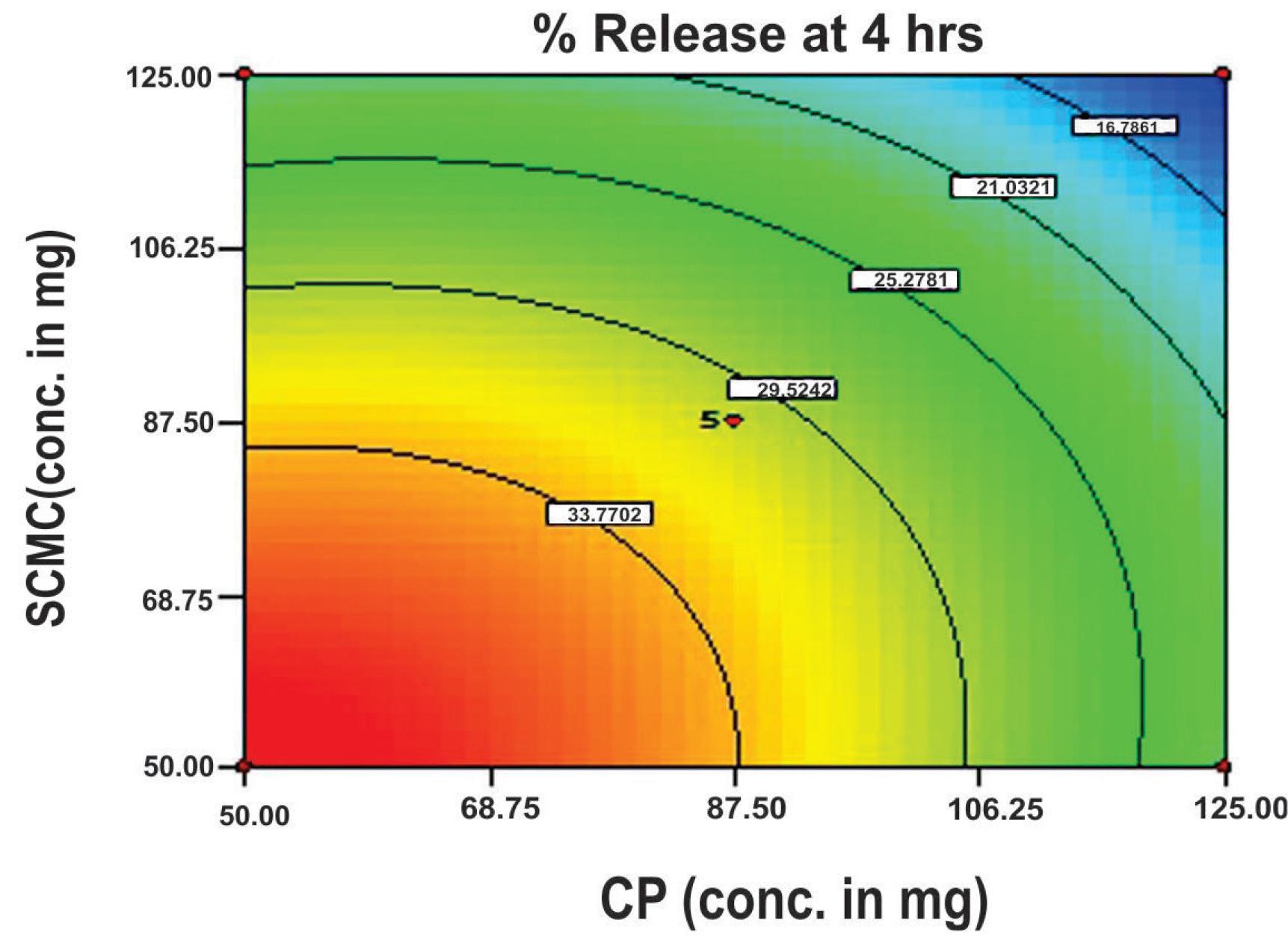
The response surface plot (Figure 6) and contour plot (Figure 7) show a steady-state decline in the value of release at 4 hours (rel4hrs), as the concentration of either polymer increases (i.e., CP and SCMC). However, the slowing influence of SCMC is somewhat more pronounced when compared to CP. The enhanced release-slowing ability of SCMC was also observed by Singh et al. (2006)SINGH, B.; CHAKKAL, S.K.; AHUJA, N. Formulation and optimization of controlled release mucoadhesive tablets of atenolol using response surface methodology. AAPS PharmSciTech., v.7, p.e3, 2006. and Varshosaz et al. (2006)VARSHOSAZ, J.; TAVAKOLI, N.; KHEIROLAHI, F. Use of hydrophilic natural gums in formulation of sustained-release matrix tablets of tramadol hydrochloride. AAPS PharmSciTech., v.7, p.e24, 2006.. Similarly, a decline in the release of the drug reaches its maximum when the highest levels of both polymers are used (i.e., 125 mg for each polymer).
Response surface plot showing the influence of CP and SCMC on the rel4hrs value of mucoadhesive tablet formulations of flurbiprofen.
Contour diagram showing the influence of CP and SCMC on the rel4hrs value of mucoadhesive tablet formulations of flurbiprofen.
Figures 8 and 9 also depict linear trends in the release patterns of the drug, but in a descending order. The release rate of the drug decreases to a great extent with increasing amounts of polymers. At lower levels of both polymers, about 80% of the drug is released within 12 hours, but as the level of the polymers increases, a gradual decline is observed in the release of the drug, and only 55% of the drug is released. By keeping SCMC concentrations at a lower level and increasing the concentration of CP, a decline in the release of the drug can be confirmed.
Response surface plots showing the influence of CP and SCMC on the rel12hrs value of mucoadhesive tablet formulations of flurbiprofen.
Contour diagram showing the influence of CP and SCMC on the rel12hrs value of mucoadhesive tablet formulations of flurbiprofen.
The response surface plot and contour plot also explain the effect of polymers on the bioadhesive strength f of the matrix tablet. Figures 10 and 11 portray the linear fashion of the bioadhesive strength f in an ascending order with increasing amounts of polymers. However, the more pronounced effect of CP is observed when compared to SCMC, which is also observed in previous studies by Singh et al. (2006)SINGH, B.; CHAKKAL, S.K.; AHUJA, N. Formulation and optimization of controlled release mucoadhesive tablets of atenolol using response surface methodology. AAPS PharmSciTech., v.7, p.e3, 2006. and Suryakanta et al. (2011)SURYAKANTA, S.; DINDA, S.C.; SARWAR, B.; SRUTI, J.; VIKAS, S.; BHANOJI, R. Design and characterization of oral sustained release mucoadhesive matrix tablets of didanosine. Asian J. Pharm. Sci. Res., v.1, p.38-60, 2011..
Response surface plot showing the influence of CP and SCMC on the value of bioadhesive strength (f) of mucoadhesive tablet formulations of flurbiprofen.
Contour diagrams showing the influence of CP and SCMC on the value of bioadhesive strength of mucoadhesive tablet formulations of flurbiprofen
CONCLUSION
Kinetic modeling showed that best fit model was the Korsmeyer-Peppas model, with non-Fickian diffusion tending towards zero-order release, indicating that the tablets can be successfully employed as a once daily, oral, controlled-release drug delivery system. The high bioadhesive strength of the tablets increases its gastrointestinal residence time and eventually improves the extent of bioavailability. However, proper balancing between the different levels of both polymers is necessary to attain proper bioadhesion, and the presence of CP is necessary for increased bioadhesion. FTIR studies of a selected formulation (F9) showed no combined effect by changing the peak symmetry and position. Therefore, it can be concluded that there is no interaction between the drug and formulation variables. A high degree of prediction obtained using RSM corroborates that a two-factor CCD is quite efficient in optimizing drug delivery systems that exhibit non-linearity in response(s).
REFERENCES
- ATKINSON, A.C.; DONEV, A.N. Optimum experimental designs. Oxford: Oxford University Press, 1992. p. 132-189.
- BOX, G.E.P.; WILSON, K.B. On the experimental attainment of multifactorial conditions. J. Roy. Statist. Soc., v.13, p.1-45, 1951.
- DAVE, B.S.; AMIN, A.F.; PATEL, M.M. Gastroretentive drug delivery system of ranitidine hydrochloride: formulation and in vitro evaluation. AAPS PharmSciTech., v.5, p.e34, 2004.
- DOLLERY, C. (Ed.). Therapeutic drugs. New York: Churchill Livingstone, 1991. p.297-299.
- DUCHEN, D.; TOUCHAR, F.; PEPPAS, N.A. Pharmaceutical and medicinal aspects of bioadhesive systems for drug administration. Drug Dev. Ind. Pharm., v.14, p.283-318, 1988.
- FORD, J.L.; RUBINSTEIN, M.H.; HOGAN, J.E. Formulation of sustained release promethazine hydrochloride tablets using hydroxypropyl methyl cellulose matrices. Int. J. Pharm., v.24, p.327-338, 1985.
- HOU, S.Y.; COWLES, V.E.; BERNER, B. Gastric retentive dosage forms: a review. Crit. Rev. Ther. Drug Carrier. Syst., v.20, p.459-497, 2003.
- KORSMEYER, R.W.; GURNEY, R.; DOELKER, E.; BURI, P.; PEPPAS, N.A. Mechanisms of solute release from porous hydrophilic polymers. Int. J. Pharm., v.15, p.25-35, 1983.
- KORSMEYER, R.W.; GURNY, R.; DOELKER, E.; BURI, P.; PEPPAS, N.A. Mechanisms of potassium chloride release from compressed, hydrophilic polymeric matrices: effect of entrapped air. J. Pharm. Sci., v.72, p.1189-1191, 1983a.
- LAVELLE, E.C. Targeted delivery of drugs to the gastrointestinal tract. Crit. Rev. Ther. Drug Carrier. Syst., v.18, p.341-386, 2001.
- MANDAL, U.; GOWDA, V.; GHOSH, A.; SELVAN, S.; SOLOMAN, S.; PAL, T.K. Formulation and optimization of sustained release matrix tablet of metformin HCl 500 mg using response surface methodology. Yakugaku. Zasshi., v.127, p.1281-1290, 2007.
- PEPPAS, N.A.; SAHLIN, J.J. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. Int. J. Pharm., v.57, p.169-172, 1989.
- PEPPAS, N.A.; SAHLIN, J.J. Hydrogels as mucoadhesive and bioadhesive materials: a review. Biomaterials, v.17, p.1553-1561, 1996.
- PHILIP, A.K.; PATHAK, K. Osmotic flow through asymmetric membrane: A mean for controlled delivery of drugs with varying solubility. AAPS PharmSciTech., v.7, p.E1-E11, 2006.
- PONCHEL, G.; TOUCHARD, F.; DUCHENE, D.; PEPPAS, N.A. Bioadhesive analysis of controlled release systems. I. Fracture and interpenetration analysis in poly (acrylic acid) containing systems. J. Control. Release, v.5, p.129-141, 1987.
- PONCHEL, G.; IRACHE, J.M. Specific and non-specific bioadhesive particulate systems for oral delivery to the gastrointestinal tract. Adv. Drug. Deliv. Rev., v.34, p.191-219, 1998.
- SHAH, S.N.H.; ASGHAR, S.; CHAUDHARY, M.A.; AKASH, M.S.; REHMAN, N.; BAKSH, S. Formulation and evaluation of natural gum-based sustained release matrix tablets of flurbiprofen using response surface methodology. Drug. Dev. Ind. Pharm., v.35, p.1470-1478, 2009.
- SINGH, B.; MEHTA, G.; KUMAR, R.; BHATIA, A.; AHUJA, N.; KATARE, O.P. Design, development and optimization of nimesulide-loaded liposomal systems for topical application. Curr. Drug Deliv., v.2, p.143-153, 2005c.
- SINGH, B.; CHAKKAL, S.K.; AHUJA, N. Formulation and optimization of controlled release mucoadhesive tablets of atenolol using response surface methodology. AAPS PharmSciTech., v.7, p.e3, 2006.
- SINGH, B.; KUMAR, R.; AHUJA, N. Optimizing drug delivery systems using systematic "design of experiments". Part I: Fundamental aspects. Crit. Rev. Ther. Drug Carrier. Syst., v.22, p.27-105, 2005a.
- SINGH, B.; DAHIYA, M.; SAHARAN, V.; AHUJA, N. Optimizing drug delivery systems using systematic "design of experiments". Part II: Retrospect and prospects. Crit. Rev. Ther Drug Carrier. Syst., v.22, p.215-294, 2005b.
- SKOUG, J.W.; MIKELSONS, M.V.; VIGNERON, C.N.; STEMM, N.L. Qualitative evaluation of the mechanism of release of matrix sustained release dosage forms by measurement of polymer release. J. Control. Release, v.27, p.227-245, 1993.
- SURYAKANTA, S.; DINDA, S.C.; SARWAR, B.; SRUTI, J.; VIKAS, S.; BHANOJI, R. Design and characterization of oral sustained release mucoadhesive matrix tablets of didanosine. Asian J. Pharm. Sci. Res., v.1, p.38-60, 2011.
- THEEUWES, F. OROS Osmotic system development. Drug. Dev. Ind. Pharm., v.7, p.1331-1357, 1983.
- VAITHIYALINGAM, S.R.; SASTRY, S.V.; DEHON, R.H.; REDDY, I.K.; KHAN, M.A. Long-term stability characterization of a controlled release gastrointestinal therapeutic system coated with cellulose acetate pseudolatex. Pharmazie, v.56, p.66-69, 2001.
- VARSHOSAZ, J.; TAVAKOLI, N.; KHEIROLAHI, F. Use of hydrophilic natural gums in formulation of sustained-release matrix tablets of tramadol hydrochloride. AAPS PharmSciTech., v.7, p.e24, 2006.
- VAZQUES, M.J.; PEREZ, M.B.; GOMEZ, J.L.; MARTINEZ, P.R.; SOUTO, C.; CONCHEIRO, A. Influence of technological variables on release of drugs from hydrophilic matrices. Drug Dev. Ind. Pharm., v.18, p.1355-1375, 1992.
- VIJAYALAKSHMI, P.; DEVI, V.K.; NARENDRA, C.; SRINAGESH, S. Development of extended zero-order release gliclazide tablets by central composite design. Drug Dev. Ind. Pharm., v.34, p.33-45, 2008.
- WOODLEY, J. Bioadhesion: new possibilities for drug administration? Clin. Pharmacokinet., v.40, p.77-84 2001.
Publication Dates
-
Publication in this collection
Jul-Sep 2014
History
-
Received
09 Mar 2013 -
Accepted
07 Nov 2013