Abstract
This paper describes a model for the analysis of multilay-ered chiral structures containing planar electric and magnetic scattering elements of arbitrary shape, illuminated by an elliptically polarized plane wave. The particular case of a single chiral layer is analyzed and the scattering matrices for single and dual electric and/or magnetic dipole distributions are derived in an original way. As an application, the polarimetric response of a short electric or magnetic dipole is directly obtained from their scattering matrix.
Chiral medium; electromagnetic scattering; Green's functions; layered media; radar remote sensing; spectral fields
Scattering analysis of planar electric and magnetic dipoles in multilayered chiral structures
N. R. RabeloI; J. C. da S. LacavaI; D. FernandesI; S. J. S. Sant'AnnaII
ILaboratório de Antenas e Propagação, Instituto Tecnológico de Aeronáutica, Pr. Mal. Eduardo Gomes, 50 12228-900 São José dos Campos - SP, Brazil, {nrrabelo, lacava, david}@ita.br
IIDivisão de Processamento de Imagem, Instituto Nacional de Pesquisas Espaciais, Av. dos Astronautas, 1758 12227-010 São José dos Campos - SP, Brazil, sidnei@dpi.inpe.br
ABSTRACT
This paper describes a model for the analysis of multilay-ered chiral structures containing planar electric and magnetic scattering elements of arbitrary shape, illuminated by an elliptically polarized plane wave. The particular case of a single chiral layer is analyzed and the scattering matrices for single and dual electric and/or magnetic dipole distributions are derived in an original way. As an application, the polarimetric response of a short electric or magnetic dipole is directly obtained from their scattering matrix.
Index Terms: Chiral medium, electromagnetic scattering, Green's functions, layered media, radar remote sensing, spectral fields.
I. INTRODUCTION
The development of polarimetric synthetic aperture radars (PolSAR) introduced new possibilities of active microwave remote sensing of the Earth [1], [2]. By containing full amplitude and phase information from each SAR image resolution cell, PolSAR signatures permit better target discrimination and classification when compared to single-polarization SAR data, having thus been successfully used for classification of a wide range of land cover [3], [4]. More recently, PolSAR imaging techniques have also been applied to the analysis of man-made structures and urban areas, despite the complexity added in these cases by the number and variety of elements involved in the electromagnetic scattering [5], [6].
The problem of electromagnetic scattering and propagation in structures composed of multiple layers of complex media appears often not only in microwave SAR remote sensing (e.g., stratified soil, crop and forest vegetation, snow and ice covers), but also in other diverse applications, such as: microstrip antennas, microwave monolithic integrated circuits (MMIC), printed circuit technology, mobile and wireless communications, medical imaging and diagnosing, geophysical mapping and planetary exploration. The efficient computational analysis of each of these cases requires accurate models that account for the geometric and electromagnetic characteristics of the particular structure under study, as well as for the specific electromagnetic excitation mechanism.
For practical PolSAR remote sensing applications, such as image classification and sensor calibration, several models have been developed to properly characterize the electromagnetic scattering of diverse targets [7]. For example, forest canopy models based on the Radiative Transfer (RT) theory have been largely utilized [8], providing good results when the medium consists of sparsely distributed scatterers that are small compared to the wavelength of the incident radiation. In this case, each scatterer needs to be carefully represented; a tree, for example, may be treated as a cluster of elementary scattering elements: dielectric cylinders (representing its trunk and branches) and smaller disks (for its leaves). On the other hand, taking into account the effect of multiple scattering from rough surfaces or volumetric interactions is not a simple task. Therefore, for an electrically dense medium, where scatterers are compactly distributed or the radiation frequency is such that the spacing between them is comparable to the wavelength, the fundamental RT assumption of independent scattering from the elements is no longer valid, thus requiring either complex model adjustments or a different model altogether [9].
Another important consideration for the accuracy of a PolSAR remote sensing model is the dielectric properties of the media that constitute each layer. Specialized literature reveals a variety of such properties, for instance: natural media such as rocks, snow, and certain types of soil can not usually be considered homogeneous [10]. Also, scattering from natural terrain cover can be strongly anisotropic [11], as confirmed by measurements taken along different directions of the trunk, branches and needles of certain conifers [12]. Still another example, chirality effects [13] have been observed in radar remote sensing of certain types of vegetation [14].
Among the several different parameters used in the literature for polarimetric target characterization, the scattering matrix, which combines both polarimetric and electromagnetic properties of a given target, plays an important role. Once the scattering matrix for a given target is accurately determined, other polarimetric target descriptors (e.g., its polarimetric response, radar cross section, entropy, anisotropy, or terrain azimuth slope) can be derived as by-products of the scattering matrix [1], [4].
In this context, the purpose of this article is twofold:
-
To present a model for the analysis of scattering from planar electric and magnetic elements of arbitrary shape embedded in a structure made out of multiple planar layers of chiral media, and illuminated by an elliptically polarized plane wave at oblique incidence. The devised method is based on the formalism previously developed for the study of scattering from multiple isotropic planar layers [15], [16], with proven results in microstrip antenna and remote sensing applications. The model for the isotropic structure has been extended to chiral media in a formal and methodical way [17], though at the cost of added complexity, and allows for planar electric and magnetic scattering elements of arbitrary shape.
-
To derive from such model the scattering matrices associated with planar electric and magnetic dipoles located at either one or both interfaces of a single chiral layer structure, resulting in manageable analytical expressions presented here in an original way.
For achieving these purposes the paper is organized as follows. The theory behind the computation of the electromagnetic fields present in the multilayered chiral structure is described in Section II. In Section III the general chiral model is particularized for simple scattering elements (planar thin elec- tric and magnetic dipoles) embedded in a three-layer planar structure consisting of a chiral layer between free space and an isotropic ground. The scattering matrices for several configurations of single and dual electric and/or magnetic dipoles are presented in Section IV. As applications of these analytical results, the polarimetric response of electric and magnetic dipoles is discussed in Section V.
II. MULTILAYERED CHIRAL STRUCTURE MODEL
The general structure under investigation, as depicted in Fig. 1, consists of N chiral layers confined in the z-direction between free space (the upper layer) and ground (the lower layer). The analytical development is based on a global rectangular coordinate system located atop the ground layer (z = 0). All layers are assumed to be linear, homogeneous, planar and unbounded along the transversal x and y directions. The isotropic ground layer, occupying the negative-z region, has complex permittivity εg and complex permeability µg, while free space, extending beyond z = dN, also isotropic, has permittivity ε0 and permeability µ0.
A chiral medium corresponds [18] to a reciprocal bi-isotropic medium that is capable of supporting two superimposed circularly-polarized waves, one to the left and the other to the right. Their different propagation speeds introduce a phase difference in the propagation of these two waves. Thus, if a plane, uniform, linearly-polarized electromagnetic wave is incident on a chiral medium, the observed macro-effect is the rotation of its polarization plane.
The n-th (for n = 1, 2, ... , N) chiral layer in Fig. 1 is characterized by permittivity εn, permeability µn, chiral admittance ζn, and thickness ℓn. Electric and magnetic elements of infinitesimal thickness are supposed to exist on each layer interface, i.e., at z = 0 and z = dn, of the multilayered chiral structure.
The excitation mechanism consists of an elliptically polarized plane wave illuminating at oblique incidence the z = dN interface between the uppermost chiral layer and free space. Considering the multilayered structure is located in the far range of the transmitting and the receiving antennas illustrated in Fig. 1, then the transmitted wave incident upon the z = dN interface and the scattered wave that reaches the receiving antenna can both be assumed to be plane and uniform [19]. Also, the elliptically polarized excitation wave is represented as the superposition of two linearly polarized waves, one parallel to the incidence plane (vertical polarization) and the other perpendicular to it (horizontal polarization).
The excitation wave induces on the electric and magnetic scattering elements located at the layer interfaces electric and magnetic surface current densities, respectively expressed as Jξ (x, y) = x Jξ x (x, y) + y Jξy(x, y) and Mξ (x, y) = x Mξx(x, y) + y Mξy(x, y), where boldface letters represent vectors, ξ ∈ {x, y}, and x and y are the unit vectors along the x- and the y-direction. These current densities are considered the virtual sources of the electromagnetic field within each layer, as well as of the scattered field in free space.
The electromagnetic field within any given layer is determined through the methodology described in [17], whereby the structure is treated as a boundary value problem. The analysis is carried out in the spectral domain using the full-wave technique, taking into account the surface electric and magnetic current densities induced on the scattering elements. The solution for the electromagnetic field in any of the N+2 layers, mathematically formulated in [17] and schematically depicted in the block diagram on Fig. 2, can be summarized as follows:
-
First, the wave equations for each of the N chiral layers, free space, and ground are solved in the Fourier domain, resulting in a system of differential equations;
-
Next, the application of the proper electromagnetic boundary conditions at each interface yields a set of 4 (N+1) equations in an equal numbers of unknowns, whose solution leads to the spectral electric and magnetic Green's functions relating each of the N+2 layers;
-
Then, the combination of the Green's functions and the spectral surface current densities allows the determination of the spectral fields at any point of the multilayered structure;
-
Finally, the electromagnetic fields in the spatial domain are obtained from the inverse double Fourier transform.
For microwave remote sensing purposes, interest is in the analysis of the far electromagnetic field scattered into free space by the multilayered structure. Since the scattered wave can be approximated by a plane wave at the receiving antenna, considered sufficiently small, the stationary phase method [19] can be used to obtain the asymptotic expressions of the scattered field in an expedient way.
From these expressions and the knowledge of the current densities on the elements, the scattering matrix is completely determined for any incidence and scattering direction. Using this method, the far scattered electric field is expressed [19] in spherical coordinates by
where θ and Φ are the unit vectors along the θ- and the Φ-direction, η0 is the intrinsic impedance of free space, k0 is the wavenumber in vacuum of the excitation wave, kxe = k0 sin θ cos Φ and kye = k0 sin θ sin Φ define the stationary phase point, r is the distance between the receiving antenna and the target, and  0z and
0z and 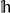 0z are the z-components of the spectral electromagnetic field in free space. As a remark, these components depend on the surface current densities induced on the elements, which can be determined by the method of moments or other alternative techniques.
0z are the z-components of the spectral electromagnetic field in free space. As a remark, these components depend on the surface current densities induced on the elements, which can be determined by the method of moments or other alternative techniques.
III. SCATTERING FROM A SINGLE CHIRAL LAYER STRUCTURE
In this section, the general case previously discussed is particularized for a single (i.e., N = 1) chiral layer with electric and magnetic currents on the interfaces z = 0 and z = d (Fig. 3).
This simpler configuration is then represented by the following system of eight equations for the eight longitudinal components of the spectral electromagnetic field, reflecting the coupling between the electric and magnetic fields
where kx and ky are the spectral variables in the x- and y- directions; ω is the angular frequency; jt, jgt, mt, and mgt (t ∈ {x, y}) are the spectral components of J, Jg, M, and Mg;  z1,
z1,  z2,
z2,  z3, and
z3, and  z4 are the spectral z-components of the electric field in the chiral layer;
z4 are the spectral z-components of the electric field in the chiral layer;  0z and
0z and 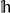 0z,
0z,  gz and
gz and 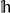 gzare respectively the spectral z-components of the electric and magnetic fields in free space and in the ground layer; and
gzare respectively the spectral z-components of the electric and magnetic fields in free space and in the ground layer; and  ,
,  ,
,  , p = ωµζ,
, p = ωµζ,  , k1 = k3 = kd = p + q, k2 = k4 = ke = q p,
, k1 = k3 = kd = p + q, k2 = k4 = ke = q p,  ,
,  ,
,  ,
,  ,
,  . As a note, kd and ke respectively represent the wavenumbers of the right and the left-handed circularly polarized components of the wave in the chiral medium.
. As a note, kd and ke respectively represent the wavenumbers of the right and the left-handed circularly polarized components of the wave in the chiral medium.
Resolution of the system of equations (2) yields the spectral field longitudinal components, from which the other transversal components can be readily determined. Each spectral field component can be expressed in terms of the electric and magnetic current densities present on the interfaces and the corresponding spectral electric and magnetic Green's functions. For illustration, the spectral electric Green's function for free space, relating the x-component of the spectral electric field to the x-component of the spectral surface electric current density on the interface between the chiral layer and free space (i.e., at the z = d plane) is given by
where
The other applicable spectral electric and magnetic Green's functions can be similarly obtained, and are listed in [17]. Thus, the spectral electric and magnetic fields can be precisely calculated once the surface current densities on the layer interfaces are numerically computed from a system of integral equations via the method of moments, using subdomain base functions and identical test functions (Galerkin method).
As mentioned in Section II, the main interest in the case of microwave remote sensing applications is not as much in the field within the confined layers and ground as it is in the far electromagnetic field scattered into free space, whose asymptotic expression is given in (1) for the electric field. For the particular structure under analysis consisting of a single chiral layer, the longitudinal components of the spectral electric and magnetic fields
0z and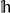 0z, determined from the resolution of the system of equations (2) following the methodology described, are given by
0z, determined from the resolution of the system of equations (2) following the methodology described, are given by
where the functions ψ0 = γ0d, and 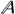 1(kxe, kye),
1(kxe, kye), 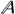 2(kxe, kye),
2(kxe, kye),  1(kxe, kye),
1(kxe, kye),  2(kxe, kye),
2(kxe, kye), 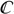 1(kxe, kye),
1(kxe, kye), 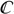 2(kxe, kye),
2(kxe, kye), 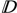 1(kxe, kye),
1(kxe, kye), 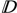 2(kxe, kye), and Δs (kxe, kye) are defined in the AppendixAppendix The functions 1(kxe, kye), 2(kxe, kye), 1(kex, kye), 2(kxe, kye), 1(kxe, kye), 2(kxe, kye), 1(kxe, kye), 2(kxe, kye), and Δs (kxe, kye) that appear in equations (4a)-(4b) are defined as follows: . As a remark, the methodology presented applies whichever the shapes of the scattering elements, as represented by the x- and y-components of the spectral electric and magnetic current distribution jt(kxe, kye), jgt(kxe, kye), mt(kxe, kye), and mgt(kxe, kye) (t ∈ {x, y}).
2(kxe, kye), and Δs (kxe, kye) are defined in the AppendixAppendix The functions 1(kxe, kye), 2(kxe, kye), 1(kex, kye), 2(kxe, kye), 1(kxe, kye), 2(kxe, kye), 1(kxe, kye), 2(kxe, kye), and Δs (kxe, kye) that appear in equations (4a)-(4b) are defined as follows: . As a remark, the methodology presented applies whichever the shapes of the scattering elements, as represented by the x- and y-components of the spectral electric and magnetic current distribution jt(kxe, kye), jgt(kxe, kye), mt(kxe, kye), and mgt(kxe, kye) (t ∈ {x, y}).
IV. SCATTERING ANALYSIS FOR ELECTRIC AND MAGNETIC DIPOLES
The scattering matrix can be regarded as the mathematical signature of a target, as it relates the scattered wave's electric field to that of the incident wave as a linear transformation of the form
where the scattering matrix, denoted by [S], is a 2x2 complex matrix, whose elements - of dimension of length - are a function of the electromagnetic properties, the shape and orientation of the target, and of the frequency and incidence angle of the illuminating wave. The diagonal (Sθθ and S ΦΦ) and the off-diagonal (SθΦand S Φθ) elements are respectively called the co- and cross-polarized components. The scattering matrix is a comprehensive parameter in polarimetric SAR analysis, providing complete information about the scattering mechanism and from which other polarimetric features used to describe the target can be derived.
The scattering matrix of electric and magnetic elements embedded in multilayered structures made out of chiral layers can be calculated following a procedure similar to the one utilized in [15] for multiple isotropic layers. As described in [1], the associated spherical coordinate system (r, θ, Φ) is related to the (k, v, h) system, defined in terms of the vertical and horizontal polarization components of the excitation wave. The spectral electric and magnetic current densities induced on the scattering elements are dependent on the polarization being vertical or horizontal, as indicated by the superscripts (v, h) that appear atop the current densities and the field components in the equations that follow. The reciprocity condition for chiral media applies to the off-diagonal elements of the scattering matrix; thus, the amplitudes of the far spectral electromagnetic field scattered into free space due to each polarization component are related by
The results obtained in Section III for a single chiral layer can be further simplified if the scattering elements are such that their dimension along one of the transversal directions (say, along the x-axis) is much larger than the one along the orthogonal direction (i.e., the y-axis, in this case). Under this circumstance, the orthogonal component of the corresponding surface current density can be neglected. This condition corresponds to having electric and magnetic dipoles as the scattering elements located at the layer interfaces.
Electric and magnetic dipoles located at either one or both interfaces, and oriented along parallel or perpendicular directions in relation to one another, can be taken into account by considering the linear combination of the corresponding current components in equations (4a) and (4b). This approach has been utilized to compute the scattering matrices of the single chiral layer structure depicted in Fig. 3 for several dipole distributions, namely:
-
single electric or magnetic dipole atop the chiral layer or the ground layer;
-
dual parallel electric, magnetic, or electric and magnetic dipoles atop the chiral layer and the ground layer;
-
dual perpendicular electric, magnetic, or electric and magnetic dipoles atop the chiral layer and the ground layer.
For each of these cases, the corresponding co-polarized (Sθθ and S ΦΦ) and cross-polarized (SθΦand S Φθ) elements of the scattering matrix [S] have been calculated in a straightforward manner following the methodology presented in the previous sections. One notes that, for practical purposes, the basic dipole orientation is considered to be along the x-direction (the y-direction being thus the perpendicular one), since the layers are assumed to be unbounded along the transversal plane, such that the use of absolute directions becomes irrelevant. The scattering matrix defined in (5) can be rewritten in the form
where the elements Sθθ, SθΦ, S Φθ and SΦΦare listed in Table I.
V. APPLICATIONS
As previously mentioned, once the scattering matrix is determined, one can directly derive from it other characteristic parameters of the scattering target, such as its radar cross-section (RCS), α-angle, directivity function, and polarimetric response [20].
As an initial application, the scattering matrix and the related characteristic parameters of a short electric dipole atop a single chiral layer have been derived and analyzed for the L-, C- and X-bands in [20] and [21]. This analysis is equivalent to taking the scattering matrix defined in (7) with the s-elements listed on the second row (Electric at z = d) of Table I.
Subsequently, short magnetic dipoles at either the lower or the upper interface of a three-layer structure containing a chiral layer in-between (Fig. 3) have been analyzed. This analysis is already based on the general methodology presented in the previous sections of this paper, leading to the scattering matrix defined in (7). In the case of a short magnetic dipole located at the lower interface (z = 0) the corresponding s-elements are listed on the third row (Magnetic at z = 0) of Table I; rather, if located at the upper interface (z = d), then the s-elements are those on the fourth row (Magnetic at z = d) of the table.
As an illustration of the applicability of this systematic procedure, the polarimetric response of electric and magnetic dipoles will now be compared. As a reminder, the polarimetric response is the graphical representa-tion of the target scattering cross-section as a function of the ellipticity and the orientation angles of the transmitted electromagnetic wave [1], [20]. The chiral structure under analysis here is depicted in Fig. 3, for ε = 2ε0, εg = ε0, µ = µg = µ0, loss tangents tan δ = 3.0×10-4 (chiral layer) and tan δg = 1.0×10-2 (ground layer), and L-band (1.25 GHz). The analysis considers two values of the chiral layer thickness (d = 24 mm and d = 32 mm), as well as different values of the chiral medium admittance (i.e. ζ = 0.0 to 10.0 mS).
From the scattering matrix defined in (7), with the corresponding s-elements listed in Table I, the co-polarized and the cross-polarized cases of the polarimetric response of a short electric or magnetic dipole at either the lower or the upper interface can be calculated. For illustration, the polarimetric response of a short electric dipole atop the chiral layer for d = 32 mm, and that of a short magnetic dipole at the ground - chiral layer interface for d = 24 mm are depicted in Fig. 4 and Fig. 5 respectively. Shown in these figures are the surface of the polarimetric response, where the ellipticity angle and the orientation angle define the transversal plane, as well as its respective contour graphic for four values of the chiral admittance (i.e. ζ = 0.0, 3.0, 6.0, and 9.0 mS). The maximum value of the co-polarized response is indicated on the contour graphic by the intersection of the two dashed lines. These results make visible the effect of chirality (represented by the chiral admittance) of the confined layer on the shape and the level of the co-polarized and the cross-polarized polarimetric responses of the structure.
Following this methodology, the effect of the chirality on the polarimetric response has been analyzed for further cases of a short electric or magnetic dipole at the lower and the upper interface of the three-layer structure. Results for the co-polarized polarimetric response maxima as a function of the chiral admittance (from 0.0 mS to 10.0 mS in 0.5-mS steps) for two different values of the chiral layer thickness (d = 24 mm and d = 32 mm) are presented in Fig. 6, where the blue curve (square markers) represents the electric dipole case and the red curve (triangular markers) the magnetic dipole case. These results show that the chiral layer thickness considerably affects the loci of the points of maximum, and also that this effect is more prominent in the case of the short electric dipole.
VI. FINAL COMMENTS
The methodology previously developed for the computation of the electromagnetic fields in multilayered achiral structures has been extended to chiral media, with either or both types of scattering elements, electric and magnetic, present at any layer interface. The field expressions so obtained, in terms of the electric and magnetic Green's functions, have then been directly used for the computation of the scattering matrix of a multilayered chiral structure. As an application of this methodology, the scattering matrices for several distributions of single and dual electric and/or magnetic dipoles in a single chiral layer structure have been calculated. Once the scattering matrix is determined, other characteristic parameters of a scattering target - such as the polarimetric response, for example - can be directly derived from it. The extension of this method to the analysis of multiple anisotropic layers is currently under way.
Received 6 Jan. 2012; for review 10 Feb. 2012; accepted 20 June 2012
- [1] F. T. Ulaby and C. Elachi, Radar Polarimetry for Geoscience Applications Norwood, MA: Artech House, 1990.
- [2] R. Touzi, W. M. Boerner, J. S. Lee, and E. Lueneburg, "A review of polarimetry in the context of synthetic aperture radar: concepts and information extraction." Can. J. Remote Sensing, vol. 30, no. 3, pp. 380407, June 2004.
- [3] J. S. Lee, M. R. Grunes, E. Pottier, and L. Ferro-Famil, "Unsupervised terrain classification preserving polarimetric scattering characteristics," IEEE Trans. Geosci. Remote Sensing, vol. 42, no. 4, pp. 722-731, Apr. 2004.
- [4] J. S. Lee and E. Pottier, Polarimetric Radar Imaging - From Basics to Applications Boca Raton, FL: CRC Press, 2009.
- [5] G. Franceschetti, A. Iodice, and D. Riccio, "A canonical problem in electromagnetic backscattering from buildings," IEEE Trans. Geosci. Remote Sensing, vol. 40, no. 8, pp. 1787-1801, Aug. 2002.
- [6] J. S. Lee, E. Krogager, T. L. Ainsworth, and W. M. Boerner, "Polarimetric analysis of radar signature of a manmade structure," IEEE Geosci. Remote Sensing Letters, vol. 3, no. 4, pp. 555-559, Oct. 2006.
- [7] A. K. Fung, Microwave Scattering and Emission Models and Their Applications Norwood, MA: Artech House, 1994.
- [8] Y. Lin and K. Sarabandi, "A Monte Carlo coherent scattering model for forest canopies using fractal-generated trees," IEEE Trans. Geosci. Remote Sensing, vol. 37, no. 1, pp. 440-451, Jan. 1999.
- [9] H. T. Ewe and H. T. Chuah, "Electromagnetic scattering from an electrically dense vegetation medium," IEEE Trans. Geosci. Remote Sensing, vol. 38, no. 5, pp. 2093-2105, Sept. 2000.
- [10] C. D. Moss, F. L. Teixeira, Y. E. Yang, and J. A. Kong, "Finite-difference time-domain simulation of scattering from objects in continuous random media," IEEE Trans. Geosci. Remote Sensing, vol. 40, no. 1, pp. 178-186, Jan. 2002.
- [11] S. R. Cloude, J. Fortuny, J. M. Lopez-Sanchez, and A. J. Sieber, "Wide-band polarimetric radar inversion studies for vegetation layers," IEEE Trans. Geosci. Remote Sensing, vol. 37, no. 5, pp. 2430-2441, Sept. 1999.
- [12] A. Franchois, Y. Piñeiro, and R. H. Lang, "Microwave permittivity measurements of two conifers," IEEE Trans. Geosci. Remote Sensing, vol. 36, no. 5, pp. 1384-1395, Sept. 1998.
- [13] E. Krogager, "Aspects of polarimetric radar imaging," Ph.D. thesis, Technical University of Denmark, Danish Defense Research Establishment, 1993.
- [14] S. R. Cloude, "Helicity in radar remote sensing," Proc. IEEE IGARSS 2002, Piscataway, NY, 2002, vol. 1, pp. 411-413.
- [15] S. J. S. Sant'Anna, J. C. S. Lacava, and D. Fernandes, "Closed form expressions for scattering matrix of simple targets in multilayer structures," Proc. IEEE IGARSS 2007, Barcelona, Spain, July 2007, pp. 714-717.
- [16] S. J. S. Sant'Anna, J. C. S. Lacava, and D. Fernandes, "Evaluation of the scattering matrix of flat dipoles embedded in multilayer structures," PIERS Online, vol. 4, no. 5, pp. 536-540, 2008
- [17] S. J. S. Sant'Anna, "Electromagnetic scattering modeling of multilayer structures with applications in microwave remote sensing", Ph.D. thesis, Instituto Tecnológico de Aeronáutica (ITA), Brazil, 2009. (In Portuguese).
- [18] I. V. Lindell, A. H. Sihvola, S. A. Tretyakov, and A. J. Viitanen, Electromagnetic Waves in Chiral and Bi-Isotropic Media Norwood, MA: Artech House, 1994.
- [19] R. E. Collin and F. J. Zucker, Antenna Theory: Part 1 NewYork: McGraw-Hill, 1969.
- [20] S. J. S. Sant'Anna, J. C. S. Lacava, and D. Fernandes, "Electromagnetic characteristics of simple targets embedded in chiral multilayer structures," Proc. IEEE IGARSS 2010, Honolulu, HI, July 2010, pp. 3031-3034.
- [21] N. R. Rabelo, S. J. S. Sant'Anna, J. C. S. Lacava, and D. Fernandes, "Scattering analysis of flat electric dipoles on multilayer chiral structures," Proc. EuCAP 2010, Barcelona, Spain, Apr. 12-16, 2010.
Appendix
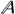
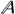
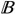
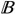
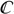
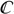
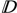
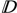
The functions
1(kxe, kye),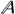 2(kxe, kye),
2(kxe, kye), 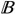 1(kex, kye),
1(kex, kye), 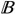 2(kxe, kye),
2(kxe, kye), 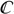 1(kxe, kye),
1(kxe, kye), 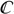 2(kxe, kye),
2(kxe, kye), 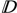 1(kxe, kye),
1(kxe, kye), 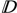 2(kxe, kye), and Δs (kxe, kye) that appear in equations (4a)-(4b) are defined as follows:
2(kxe, kye), and Δs (kxe, kye) that appear in equations (4a)-(4b) are defined as follows:
Publication Dates
-
Publication in this collection
16 July 2012 -
Date of issue
June 2012
History
-
Received
06 Jan 2012 -
Accepted
20 Feb 2012 -
Reviewed
10 Feb 2012

















