Leaf Area Estimate of Erythroxylum simonis Plowman by Linear Dimensions

ABSTRACT

This research aimed to determine an equation to estimate the leaf area of Erythroxylum simonis using the length and width of leaf blades. Two hundred leaf blades of this species were collected in Mata do Pau-Ferro, a State Park located in Areia, PB, Brazil. Regression analyses were used to determine the estimation equations. The linear, linear without intercept, quadratic, cubic, power and exponential statistical models were used. The criteria used for model selection were based on an examination of the coefficient of determination, the Akaike information criterion and standard error of the estimate. All the equations presented can be used to estimate the leaf area of E. simonis. From a practical point of view, the linear regression equation without intercept involving the product between length and width is recommended, using the equation Y=0.6426*LW, which corresponds to 64.26% of the product between length and width, with a coefficient of determination of 0.9936.

Keywords:
biometry; non-destructive method; Erythroxylaceae

1. INTRODUCTION

Popularly known “guarda-orvalho”, the Erythroxylum simonis Plowman (Erythroxylaceae) is an understory species, endemic to the Northeast region, being reported in the states of Paraíba, Ceará, Pernambuco, Sergipe, and Rio Grande do Norte, found in Atlantic Forest rainforests or in countryside forest environments known as “Altitude Marshes” ( Loiola et al., 2007 ; Loiola & Costa-Lima, 2015 ). This species is extremely important for the preservation of genetic resources that are endemic to these regions and to ensure a food source for their fauna during different periods, cooperating with seed propagation, especially in disturbed environments such as the Altitude Marshes ( Fabricante, 2013 ).

Due to this species’ importance, it is necessary to perform ecophysiological studies of its traits in terms of growth, development and propagation. In most studies, determining leaf area, an element considered by some as the most important parameter to evaluate vegetation growth, is fundamentally important ( Bianco et al., 1983 ; Benincasa, 1988 ). This is one of the most difficult variables to measure because it requires expensive equipment or employs destructive techniques ( Bianco et al., 1983 ; Taiz & Zeiger, 2004 ).

There are many methods to determine the leaf area, which can be classified as destructive or non-destructive, direct or indirect ( Marshall, 1968 ). The destructive methods, are usually simple and precise ( Malagi et al., 2011 ) but can be more complicated, demanding time and labor ( Marcolini et al., 2005 ), and also result in leaf destruction. Marshall (1968) states that it is important to employ a non-destructive method to measure leaf area because it allows several evaluations of the same plant with precision and speed. Therefore, the determination of the leaf area may be estimated using the dimensional parameters of the leaf (length, width, and length by width), which present good correlations with the leaf surface, adapting regression equations to obtain an estimate between the real leaf area and the linear dimensional parameters of the leaf without destroying the sample ( Nascimento et al., 2002 ; Lizaso et al., 2003 ). This non-destructive method has been used successfully in several other studies, both in cultivated ( Oliveira & Santos, 1995 ; Uzun & Çelik, 1999 ; Lizaso et al., 2003 ; Blanco & Folegatti, 2005 ; Demirsoy et al., 2005 ; Tsialtas & Maslaris, 2005 ; Antunes et al., 2008 ; Pompelli et al., 2012 ) and forest species (Silva et al., 2007 , 2013 ; Cabezas-Gutiérrez et al., 2009 ; Queiroz et al., 2013 ; Mota et al., 2014 ; Keramatlou et al., 2015 ).

Therefore, the objective of the present study is to determine a regression equation to obtain an estimate of Erythroxylum simonis leaf area based on the linear dimensional parameters of the leaf blade.

2. MATERIAL AND METHODS

This study was developed in Mata do Pau-Ferro State Park, located 5 km west of the center of the city of Areia-PB, Northeast of Brazil, at a latitude of 6°58’12” S and longitude 35°42’15” W, totaling an approximate area of 608 ha ( Figure 1 ). The region presents an altitude that varies between 400 and 600 m, an annual average temperature of 22°C ( Ribeiro et al., 2018 ), and a tropical climate classified, according to Köppen (1936) , as As.

Figure 1
Geographic location of the State Park of Mata do Pau-Ferro, Areia, State of Paraíba, Northeast Brazil.

Two hundred E. simonis leaf blades were gathered. They did not present any deformities originating from external factors (healthy leaves), such as pests or diseases. Ten different-sized leaves were sampled in each individual, deposited in plastic bags and taken to the laboratory to determine their leaf blade length (L) and width (W) ( Figure 2 ), and to calculate their real leaf area (LA). All leaf blades were digitalized with a table scanner, with the addition of a certain scale ( Figure 3 A and B). To perform the measurements, public domain ImageJ® ( Powerful Image Analysis) software was employed. In ImageJ, the images were contrasted to facilitate the leaf area determination ( Figure 3 B) and then all measurements were performed. In Figure 3 (A and B), we can see different-sized, full E. simonis leaves and in digitalized images to perform the measurements.

Figure 2
Length (L) and width (W) of the leaf blade used to create models to estimate the leaf area in Erythroxylum simonis.

Figure 3
(A) Erythroxylum simonis scanned leaves of different sizes used to determine the leaf area, using ImageJ software; (B) Scanned leaves with contrasting background used to determine the leaf area, using ImageJ software.

To choose the adjusted equation that determines the E. simonis leaf area estimate, regression studies were performed, employing the following statistical models: linear, linear without intercept, quadratic, cubic, power, and exponential ( Table 1 ). The Y value was estimated for X, in which the values were length (L), width (W), or the product (LxW). The best equations were chosen based on the greatest coefficient of determination estimated (R²), lowest Akaike information criterion (AIC), and the lowest standard error of the estimate ( Peressin et al., 1984 ). The regression analyses were obtained through the Datafit v. 9.1.32 software (Oakdale Engineering, Oakdale, PA, USA).

Table 1
Denomination and representation of equation models adjusted to estimate the leaf area of Erythroxylum simonis.

Denomination of equation	Representation of equation
Linear	y = ax + b
Linear without intercept (0.0)	y = bx
Quadratic	y = ax2 + bx + c
Cubic	y = ax3 + bx2 + cx + d
Power	y = axb
Exponential	y = abx

3. RESULTS AND DISCUSSION

E. simonis leaf blades presented an average length (L) of 4.81 cm, varying from 1.12 to 9.38 cm. Regarding the width (W), they presented a variation of 0.58 to 4.01 cm, with an average value of 2.00 cm. The real leaf area values varied from 0.51 to 23.4 cm² , with an average of 6.98 cm² ( Table 2 ).

Table 2
Minimum, maximum, mean, median, standard deviation, standard error, and coefficient of variation (C.V.) for length (L), width (W), length by width (LxW), and leaf area (LA) of 200 Erythroxylum simonis leaf blades.

Statistical	Length (cm)	Width (cm)	LxW (cm2)	Leaf area (cm2)
Minimum	1.120	0.580	0.640	0.516
Maximum	9.380	4.010	37.650	23.479
Mean	4.819	2.007	10.703	6.983
Median	4.795	1.940	9.185	5.886
Standard deviation	1.596	0.685	6.783	4.372
Standard error	0.113	0.048	0.480	0.309
C.V. (%)	33.130	34.140	63.370	62.620

Regarding the data variability, lower variation coefficients were registered for the linear dimensions of width and length (CV = 33.13 and 34.14%, respectively), and greater variability for the product (LxW) and leaf area (CV = 63.37 and 62.62%) ( Table 2 ). Other studies also presented greater variability for LxW regarding the L and W dimensions (Cargnelutti et al., 2012 , 2015 ; Toebe et al., 2012 ).

Table 3 presents the percentage distribution of the 200 E. simonis leaf blades regarding their size range. We notice that 59.5% of the leaf area is related to leaves that vary from 0.05 to 7.0 cm², which indicates that most leaves of that plant are small.

Table 3
Percentage distribution of the real leaf area (LA) of 200 Erythroxylum simonis leaf blades, in relation to different size ranges.

LA (cm2)	(%)
[0.50-3.50]	25.0
[3.51-7.0]	34.5
[7.01-10.0]	16.0
[10.01-13.0]	14.5
[13.01-16.0]	7.0
[16.01-24.0]	3.0

The results with the equations obtained from the regression analysis linking the real leaf area (Y) and the linear parameters of length (L), width (W), and the product of length and width (LxW) are presented in Table 4 . We can also notice that all regression equations presented allow us to satisfactorily estimate this species’ leaf area, with every coefficient of determination (R²) greater than 0.84, which indicates that at least 84% of the variations of the E. simonis leaf areas were explained by the determined equations, using this species’ leaf dimensions.

Table 4
Estimated equations, estimated standard error, coefficients of determination and Akaike information criterion as a function of linear measurements of leaf blade of Erythroxylum simonis.

Model	X (1)	S.E. (2)	R2 (3)	AIC (4)	Estimated equation
Linear	L	113.27	0.9328	1182.17	Y = - 5.7666 + 2.646x
Linear	W	0.969	0.9509	1198.09	Y = - 5.5060 + 6.226x
Linear	LxW	0.350	0.9936	671.69	Y = 0.1053 + 0.6426x
Linear (0.0)	LxW	0.350	0.9936	639.95	Y = 0.6426x
Quadratic	L	0.845	0.9626	994.82	Y = - 0.2440 + 0.1717x + 0.2483x2
Quadratic	W	0.705	0.9739	996.95	Y = - 0.7084 + 1.1006x + 1.2211x2
Quadratic	LxW	0.342	0.9939	673.41	Y = - 0.0013 + 0.6769x - 0.062x2
Cubic	L	0.847	0.9624	996.42	Y = 0.2373 - 0.1714x + 0.3223x2 - 0.0049x3
Cubic	W	0.706	0.9738	992.56	Y = - 0.1233 + 0.1251x + 1.7092x2 - 0.0751x3
Cubic	LxW	0.343	0.9938	666.73	Y = - 0.0102 + 0.6605x - 0.000009x2 - 0.000025x3
Power	L	0.843	0.9627	992.80	Y = 0.2975x1.9461
Power	W	0.705	0.9739	997.08	Y = 1.7279x1.8774
Power	LxW	0.345	0.9937	671.98	Y = 0.6885x0.9793
Exponential	L	110.10	0.9253	1169.57	Y = 0.6965*0.4323X
Exponential	W	104.56	0.9285	1113.05	Y = 0.7384*1.0092X
Exponential	LxW	82.74	0.8434	1957.93	Y = 1.9769*0.0971X

• ⁽¹⁾
  Linear measurements: length (L) and width (W);
• ⁽²⁾
  Estimated standard error;
• ⁽³⁾
  Coefficients of determination;
• ⁽⁴⁾
  Akaike information criterion.

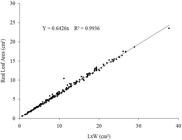
The R² value varied from 0.8434 to 0.9939; the lower value corresponds to the exponential model in which the length and width product was employed as the calculation base to estimate the leaf area of E. simonis leaves, while the greatest value of R² was obtained with the product data (LxW), through the quadratic model (R² = 0.9939) ( Table 4 ). The AIC varied from 639.95 to 1957.93. The lower value corresponds to the linear model without intercept, while the highest value obtained corresponds to the exponential model, both using the product data (LxW). Therefore, from a more practical perspective, the linear equation without intercept that presents a line crossing its origin (R² = 0.9939 and AIC = 639.95) is the most recommended because it is easier to use, which simplifies the calculation. Consequently, the E. simonis leaf area estimate may be obtained through the equation Y = 0.6426*LW, that is, it corresponds to 64.26% of the product between the leaf blade’s length and width, or 64.26% of the area given by the product (LxW) ( Figure 4 ).

Figure 4
Relation between real leaf area of Erythroxylum simonis leaves as a function of the product of length (L) by width (W) of leaf blade, by the regression equation indicated to estimate the leaf area.

There was little data dispersion regarding the resulting line. Therefore, the Y = 0.6426*LW equation may represent the real leaf area very satisfactorily ( Figure 4 ). Identical models were obtained to estimate other forest species leaf area, such as Ziziphus joazeiro (Y = 0.7931*LW) ( Maracajá et al., 2008 ), Manihot pseudoglaziovii and Manihot piauhyensi s (Y = 0.533*LW) ( Pinto et al., 2007 ), Combretum leprosum (0.7103*LW) ( Candido et al., 2013 ), and Ageratum conyzoides (Y = 0.6789*LW) ( Bianco et al., 2008 ). On the other hand, Kumar (2009) noticed that the most recommended model to estimate the Crocus sativus L.’s leaf area was the exponential (Y = 191.33*^(W)0.0037).

The equations that depend on the product (LxW) present higher coefficients of determination, lower AIC and lower standard error of the estimate for regression models in comparison with those observed for equations elaborated with L or W, except for the exponential model, in which the coefficient of determination was lower and the AIC was greater than the others (R² = 0.8434 and AIC = 1957.93) ( Table 4 ). Similar results were found in the literature for other forest species, such as Amburana cearenses, Caesalpinia ferrea, and Caesalpinia pyramidalis ( Silva et al., 2013 ), Schinopsis brasiliensis and Tabebuia aurea ( Queiroz et al., 2013 ), Acrocomia aculeata ( Mota et al., 2014 ) or even for cultivation species, such as Crambe abyssinica ( Toebe et al., 2010 ), Mangifera indica ( Lima et al., 2012 ), Malus domestica ( Bosco et al., 2012 ) and Arachis hypogae ( Cardozo et al., 2014 ), etc.

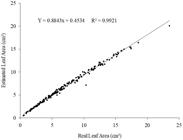
The estimated leaf area, obtained through the use of the indicated equation (Y = 0.6426*LW), ensures a satisfactory proximity to the real leaf area, since the coefficient of determination obtained through the relation between these two factors was of 0.9921, as seen in Figure 5 .

Figure 5
Relation between real leaf area and estimated leaf area by the regression equation Y = 0.6426*LW.

4. CONCLUSIONS

From a practical perspective, the E. simonis leaf area may be estimated using the equation Y = 0.6426*LW.

The exponential model is less recommendable because it presented a lower coefficient of determination and a greater AIC.

ACKNOWLEDGEMENTS

We thank to the CAPES (Coordination for the Improvement of Higher Education Personnel) for the scholarship of the first and second author.

REFERENCES

• Antunes WC, Pompelli MF, Carretero DM, DaMatta FM. Allometric models for non-destructive leaf area estimation in coffee (Coffea canephora and Coffea canephora). Annals of Applied Biology 2008; 153(1): 33-40. http://dx.doi.org/10.1111/j.1744-7348.2008.00235.x.
  » http://dx.doi.org/10.1111/j.1744-7348.2008.00235.x
• Benincasa MMP. Análise de crescimento de plantas: noções básicas Jaboticabal: FUNEP; 1988.
• Bianco S, Bianco MS, Carvalho LB. Estimativa da área foliar de Ageratum conyzoides usando dimensões lineares do limbo foliar. Acta Scientiarum. Agronomy 2008; 30(4): 519-523. http://dx.doi.org/10.4025/actasciagron.v30i4.5311.
  » http://dx.doi.org/10.4025/actasciagron.v30i4.5311
• Bianco S, Pitelli RA, Perecin D. Métodos para estimativa da área foliar de plantas daninhas. 2: Wissadula subpeltata (Kuntze) Fries. Planta Daninha 1983; 6(1): 21-24. http://dx.doi.org/10.1590/S0100-83581983000100004.
  » http://dx.doi.org/10.1590/S0100-83581983000100004
• Blanco FF, Folegatti MV. Estimation of leaf área for greenhouse cucumber by linear measurements under salinity and grafting. Scientia Agrícola 2005; 62(4): 305-309. http://dx.doi.org/10.1590/S0103-90162005000400001.
  » http://dx.doi.org/10.1590/S0103-90162005000400001
• Bosco LC, Bergamaschi H, Cardoso LS, Paula VA, Casamali B. Seleção de modelos de regressão para estimar a área foliar de macieiras ‘Royal Gala’ e ‘Fuji Suprema’ sob tela antigranizo e em céu aberto. Revista Brasileira de Fruticultura 2012; 34(2): 504-514. http://dx.doi.org/10.1590/S0100-29452012000200024.
  » http://dx.doi.org/10.1590/S0100-29452012000200024
• Cabezas-Gutiérrez M, Peña F, Duarte HW, Colorado JF, Lora Silva L. Um modelo para la estimación del área foliar em três espécies forestales de forma no destructiva. Revista Actualidad & Divulgación Científica 2009; 12(1): 121-130.
• Candido WS, Coelho MFB, Maia SSS, Cunha CSM, Silva RCP. Modelo para estimar a área foliar de Combretum leprosum Mart. Acta Agronomica 2013; 62(1): 37-41.
• Cardozo NP, Parreira MC, Panosso AR, Volpe CA. Modelagem da Área Foliar de Duas Cultivares de Amendoim em Função das Dimensões Lineares dos Folíolos. Bioscience Journal 2014; 30(1): 101-107.
• Cargnelutti A Fo, Toebe M, Alves BM, Burin C, Kleinpaul JA. Estimação da área foliar de canola por dimensões foliares. Bragantia 2015; 74(2): 139-148. http://dx.doi.org/10.1590/1678-4499.0388.
  » http://dx.doi.org/10.1590/1678-4499.0388
• Cargnelutti A Fo, Toebe M, Burin C, Fick AL, Neu IMM, Facco G. Estimação da área foliar de mucuna cinza por meio de método não destrutivo. Ciência Rural 2012; 42(2): 238-242. http://dx.doi.org/10.1590/S0103-84782012000200009.
  » http://dx.doi.org/10.1590/S0103-84782012000200009
• Demirsoy H, Demirsoy L, Ozturk A. Improved model for the non-destructive estimation of strawberry leaf área. Fruits 2005; 60(1): 69-73. http://dx.doi.org/10.1051/fruits:2005014.
  » http://dx.doi.org/10.1051/fruits:2005014
• Fabricante JR. Sociabilidade de espécies da mata atlântica com a exótica invasora Artocarpus heterophyllus Lam. Revista de Biologia Neotropical 2013; 10(2): 18-25.
• Keramatlou I, Sharifani M, Sabouri H, Alizadeh M, Kamkar B. A simple linear model for leaf area estimation in Persian walnut (Juglans regia L.). Scientia Horticulturae 2015; 184(1): 36-39. http://dx.doi.org/10.1016/j.scienta.2014.12.017.
  » http://dx.doi.org/10.1016/j.scienta.2014.12.017
• Köppen W. Das geographische system der klimate. In: Köppen W, Geiger R, editors. Handbuch der klimatologie. Berlin: Gebruder Borntraeger; 1936.
• Kumar R. Calibration and validation of regression model for non-destructive leaf area estimation of saffron (Crocus sativus L.). Scientia Horticulturae 2009; 122(1): 142-145. http://dx.doi.org/10.1016/j.scienta.2009.03.019.
  » http://dx.doi.org/10.1016/j.scienta.2009.03.019
• Lima RT, Souza PJOP, Rodrigues JC, Lima MJA. Modelos para estimativa da área foliar da mangueira utilizando medidas lineares. Revista Brasileira de Fruticultura 2012; 34(4): 974-980. http://dx.doi.org/10.1590/S0100-29452012000400003.
  » http://dx.doi.org/10.1590/S0100-29452012000400003
• Lizaso JI, Batchelor WD, Westgate ME. A leaf área model to simulate cultivar specific expansion and senescence of maize leaves. Field Crops Research 2003; 80(1): 1-17. http://dx.doi.org/10.1016/S0378-4290(02)00151-X.
  » http://dx.doi.org/10.1016/S0378-4290(02)00151-X
• Loiola MIB, Agra MF, Baracho GS, Queiroz RT. Flora da Paraíba, Brasil: Erythroxylaceae Kunth. Acta Botanica Brasílica 2007; 21(2): 473-487. http://dx.doi.org/10.1590/S0102-33062007000200020.
  » http://dx.doi.org/10.1590/S0102-33062007000200020
• Loiola MIB, Costa-Lima JL. Erythroxylaceae in Lista de Espécies da Flora do Brasil [Internet]. Rio de Janeiro: Jardim Botânico do Rio de Janeiro; 2015 [cited 2016 June 21]. Available from: http://floradobrasil.jbrj.gov.br/jabot/floradobrasil/FB7730
  » http://floradobrasil.jbrj.gov.br/jabot/floradobrasil/FB7730
• Malagi G, Citadin I, Scariot S, Reis L. Método não destrutivo para determinação da área foliar da videira, cultivar BRS-Violeta. Revista Brasileira de Fruticultura 2011; 32(4): 1250-1254. http://dx.doi.org/10.1590/S0100-29452011005000005.
  » http://dx.doi.org/10.1590/S0100-29452011005000005
• Maracajá PB, Madalena JÁ, Araújo E, Lima BG, Linhares PC. Estimativa de área foliar de juazeiro por dimensões lineares do limbo foliar. Rev. Verde de Agroecologia 2008; 3(4): 1-5.
• Marcolini MW, Cecílio AB Fo, Barbosa JC. Equações de regressão para a estimativa da área foliar de couve-folha. Científica (Jaboticabal) 2005; 33(2): 192-198.
• Marshall JK. Methods of leaf area measurement of large and small leaf samples. Photosynthetica 1968; 2(1): 41-47.
• Mota CS, Leite HG, Cano MAO. Equações para estimar área foliar de folíolos de Acrocomia aculeta. Pesquisa Florestal Brasileira 2014; 34(79): 217-224. http://dx.doi.org/10.4336/2014.pfb.34.79.684.
  » http://dx.doi.org/10.4336/2014.pfb.34.79.684
• Nascimento IB, Farias CHA, Silva MCC, Medeiros JF, Espínola Sobrinho J, Negreiros MZ. Estimativa da área foliar do meloeiro. Horticultura Brasileira 2002; 20(4): 555-558. http://dx.doi.org/10.1590/S0102-05362002000400009.
  » http://dx.doi.org/10.1590/S0102-05362002000400009
• Oliveira M, Santos MA. Semi-empirical method to estimate canopy leaf área of vineyards. American Journal of Enology and Votiniculture 1995; 46(3): 398-391.
• Peressin VA, Pitelli RA, Perecin D. Métodos para estimativa da área foliar de plantas daninhas. 4. Cassia tora L. Planta Daninha 1984; 7(2): 48-52. http://dx.doi.org/10.1590/S0100-83581984000200004.
  » http://dx.doi.org/10.1590/S0100-83581984000200004
• Pinto MS, Andrade AP, Pereira WE, Arruda FP, Andrade MV. Modelo para estimativa da área foliar da maniçoba. Revista de Ciência Agronômica . 2007; 38(4): 391-395.
• Pompelli MF, Antunes WC, Ferreira DTRG, Cavalcante PGS, Wanderley-Filho HCL, Endres L. Allometric models for non-destructive leaf area estimation of Jatropha curcas. Biomass and Bioenergy 2012; 36(1): 77-85. http://dx.doi.org/10.1016/j.biombioe.2011.10.010.
  » http://dx.doi.org/10.1016/j.biombioe.2011.10.010
• Queiroz JE, Silva GH, Souza AG No. Avaliação estatística da área foliar através de modelos de equações em duas espécies florestais. Revista Verde de Agroecologia e Desenvolvimento Sustentável 2013; 8(1): 146-153.
• Ribeiro JES, Barbosa AJS, Lopes SF, Pereira WE, Albuquerque MB. Seasonal variation in gas exchange by plants of Erythroxylum simonis Plowman. Acta Botanica Brasílica 2018; 32(2): 287-296. http://dx.doi.org/10.1590/0102-33062017abb0240.
  » http://dx.doi.org/10.1590/0102-33062017abb0240
• Silva GH, Queiroz JE, Souza AGS No. Avaliação da área foliar de três espécies florestais ocorrentes no semiárido paraibano (Amburana cearenses, Caesalpinia ferrea, Caesalpinia pyramidalis). Revista de Biologia e Farmácia 2013; 9(3): 1-11.
• Silva PS, Cunha TM, Souza AD, Paula VF. Equations for leaf area estimation in some species adapted to the Brazilian semi-arid. Revista Caatinga 2007; 20(4): 18-23.
• Taiz L, Zeiger E. Fisiologia vegetal 3. ed. Porto Alegre: The Art of Medication; 2004.
• Toebe M, Brum B, Lopes SJ, Cargnelutti A Fo, Silveira TR. Estimativa da área foliar de Crambe abyssinica por discos foliares e por fotos digitais. Ciência Rural 2010; 40(2): 475-478. http://dx.doi.org/10.1590/S0103-84782010000200036.
  » http://dx.doi.org/10.1590/S0103-84782010000200036
• Toebe M, Cargnelutti A Fo, Burin C, Fick AL, Neu IMM, Casarotto G et al. Modelos para a estimação da área foliar de feijão de porco por dimensões foliares. Bragantia 2012; 71(1): 37-41. http://dx.doi.org/10.1590/S0006-87052012005000010.
  » http://dx.doi.org/10.1590/S0006-87052012005000010
• Tsialtas JT, Maslaris N. Leaf área estimation in a sugar beet cultivar by linear models. Photosynthetica 2005; 23(6): 477-479. http://dx.doi.org/10.1007/s11099-005-0077-z.
  » http://dx.doi.org/10.1007/s11099-005-0077-z
• Uzun S, Çelik H. Leaf área prediction models (Uzçelik-I) for different horticultural plants. Turkish Journal of Agriculture and Forestry 1999; 23(6): 645-650.

Publication Dates

• Publication in this collection
  18 June 2018
• Date of issue
  2018

History

• Received
  15 June 2017
• Accepted
  11 Aug 2017