Abstracts
The interval-valued intuitionistic fuzzy logic, an extension of fuzzy logic, integrates the concepts of interval-valued fuzzy logic and intuitionistic fuzzy logic. The former, reflects the measure of vagueness and uncertainty in the diameter of an interval. The latter considers the hesitation related to the dual construction. This paper considers an expression to interval-valued intuitionistic fuzzy implications, which can be generated by idempotent interval-valued aggregation functions acting on a pair of mutual-dual functions, an interval-valued implication and its corresponding coimplication. Then, we show under which conditions interval-valued intuitionistic fuzzy implications are diagonal preserving operators. We study not only properties of such operators which were extended to intuitionistic fuzzy logic, but also analyse properties truly intuitionistic. The canonical representation in the class of such operators and an interval version of an intuitionistic fuzzy index conclude this study.
interval-valued intuitionistic fuzzy connectives; interval-valued intuitionistic fuzzy implication; intuitionistic index
A Lógica Fuzzy Intuicionista Valorada Intervalarmente consiste em uma extensão da lógica fuzzy, integrando conceitos da lógica fuzzy valorada intervalarmente e da lógica fuzzy intuicionista. A primeira considera a hesitação relacionada com a construção dual de conjuntos fuzzy intuicionistas, enquanto a segunda reflete a medida da imprecisão e incerteza no diâmetro dos intervalos associados aos elementos de um conjunto fuzzy. Este artigo mostra que uma implicação fuzzy valorada intervalarmente (IvIFI) pode ser obtida pela ação de funções de agregação valoradas intervalarmente sobre pares de funções mutuamente duais, ou seja uma implicação e sua correspondente coimplicação valorada intervalarmente. Na construção de IvIFIs, são discutidas as condições que preservam operadores diagonais e funções duais. As principais propriedades destes operadores são estudadas, incluindo tanto as propriedades preservadas da lógica fuzzy quanto propriedades inerentes da abordagem fuzzy intuicionista. A representação canônica para a classe de IvIFIs e a versão intervalar para o operador denominado índice fuzzy intuicionista são apresentados e exemplos destes operadores concluem o estudo descrito neste trabalho.
lógica fuzzy intuicionista valorada intervalarmente; implicação fuzzy valorada intuicionista; índice intuicionista
Index, expressions and properties of interval-valued intuitionistic fuzzy implications* * This paper was presented in CNMAC 2012.
R.H.S. ReiserI; B. BedregalII,** ** Corresponding author: Benjamin Callejas Bedregal ; L. VisintinIII
ICentro de Desenvolvimento Tecnológico, CDTec, UFPel - Universidade Federal de Pelotas, 96010-610 Pelotas, RS, Brasil. E-mail: reiser@inf.ufpel.edu.br
IIDepartamento de Informática e Matemática Aplicada, DIMAP, UFRN - Universidade Federal do Rio Grande do Norte, 59078-970 Natal, RN, Brasil. E-mail: bedregal@dimap.ufrn.br
IIICentro Tecnológico, Departamento de Engenharia Elétrica, UFSC - Universidade Federal de Santa Catarina, 88040-900 Florianopolis, SC, Brasil. E-mail: lidiane.vi@hotmail.com
ABSTRACT
The interval-valued intuitionistic fuzzy logic, an extension of fuzzy logic, integrates the concepts of interval-valued fuzzy logic and intuitionistic fuzzy logic. The former, reflects the measure of vagueness and uncertainty in the diameter of an interval. The latter considers the hesitation related to the dual construction. This paper considers an expression to interval-valued intuitionistic fuzzy implications, which can be generated by idempotent interval-valued aggregation functions acting on a pair of mutual-dual functions, an interval-valued implication and its corresponding coimplication. Then, we show under which conditions interval-valued intuitionistic fuzzy implications are diagonal preserving operators. We study not only properties of such operators which were extended to intuitionistic fuzzy logic, but also analyse properties truly intuitionistic. The canonical representation in the class of such operators and an interval version of an intuitionistic fuzzy index conclude this study.
Keywords: interval-valued intuitionistic fuzzy connectives, interval-valued intuitionistic fuzzy implication, intuitionistic index.
RESUMO
A Lógica Fuzzy Intuicionista Valorada Intervalarmente consiste em uma extensão da lógica fuzzy, integrando conceitos da lógica fuzzy valorada intervalarmente e da lógica fuzzy intuicionista. A primeira considera a hesitação relacionada com a construção dual de conjuntos fuzzy intuicionistas, enquanto a segunda reflete a medida da imprecisão e incerteza no diâmetro dos intervalos associados aos elementos de um conjunto fuzzy. Este artigo mostra que uma implicação fuzzy valorada intervalarmente (IvIFI) pode ser obtida pela ação de funções de agregação valoradas intervalarmente sobre pares de funções mutuamente duais, ou seja uma implicação e sua correspondente coimplicação valorada intervalarmente. Na construção de IvIFIs, são discutidas as condições que preservam operadores diagonais e funções duais. As principais propriedades destes operadores são estudadas, incluindo tanto as propriedades preservadas da lógica fuzzy quanto propriedades inerentes da abordagem fuzzy intuicionista. A representação canônica para a classe de IvIFIs e a versão intervalar para o operador denominado índice fuzzy intuicionista são apresentados e exemplos destes operadores concluem o estudo descrito neste trabalho.
Palavras-chave: lógica fuzzy intuicionista valorada intervalarmente, implicação fuzzy valorada intuicionista, índice intuicionista.
1 INTRODUCTION
Among equivalent extensions of fuzzy sets (see, e.g., Vague Sets [16] and [6]), this paper considers the interval-valued fuzzy sets (shortly IvFSs), as introduced in [29] and [25], together with intuitionistic fuzzy sets (shortly IFSs), as presented in [2]. Both approaches are founded on the interval-valued fuzzy logic (shortly IvFL) and intuitionistic fuzzy logic (shortly IFL), respectively, which are important extensions of Fuzzy Logic (shortly FL). IFL and IvFL are closely related and both concepts are concerned with imprecision-handling strategies, see [12].
More recently, other authors have sought to improve upon the deeper understanding of uncertainty and imprecision information [4, 8] and [27]. This paper considers the interval-valued intuitionistic fuzzy logic (shortly IvIFL) with contributions from Atanassov and Gargov [1] in the eighties, integrating the concepts of IvFSs and IFSs. By the former, the measure of vagueness and uncertainty in the diameter of an interval membership degree can be modelled, and by the latter, it can be also considered the hesitation related to the dual construction modelled by an inequality, i.e., the difference between an interval membership degree and its non-membership degree is less or equal to unit interval U =[0, 1]. This approach allows to relax the complementary operation stated over fuzzy sets in FL.
One motivation for our study has been the significant performance achieved by the use of interval-valued fuzzy implications (shortly IvFIs) in some applications, such as in the area of image processing, see [9] and [17]. The fuzzy implications are essential to deductive methods in approximate reasoning, interpreting the conditional fuzzy rule in systems based on FL. In both classical and fuzzy approaches, the occurrence of various expressions of implications is evident [20]. However, extensions of fuzzy implications are not the same as in the classical ones, resulting in distinct (S-implications, QL-implications, R-implications) classes of fuzzy implications. Additionally, there are different (explicit, implicit and axiomatic) representations of these connectives. Such diversity encourages the study of IvFIs and their dual constructions, the interval-valued fuzzy coimplications (shortly IvFCs), see [23].
This paper aims to explore interval-valued intuitionistic fuzzy implications (shortly IvIFIs), in the sense of [28], which are generated by interval-valued aggregation functions (shortly IvAs) acting on mutual-dual pairs of IvFIs and IvFCs. Such construction is analogous to [8]. In previous work [28], we studied properties of IvIFI operators extending analogous properties from IFL, which are also generalizations of properties from FL. Many properties truly intuitionistic of IvIFIs (e.g. correlation coefficient, degree of compatibility and entropy of IFSs) have been considered in the literature. Here, the Atanassov's intuitionistic fuzzy sets are studied based on the intuitionistic index of each element obtained by subtracting the sum of membership and non-membership from one. Thus, an interval-valued intuitionistic fuzzy index is introduced as a generalized Atanassov's intuitionistic fuzzy index, called interval degree of indeterminacy in [2].
We also study the action of canonical representation of such fuzzy connectives (aggregations, implications and coimplications) in order to characterize the class of IvIFIs. The authors follow the approach considered in [28], showing such IvIFIs as diagonal preserving operators over which it is possible to preserve main fuzzy implication properties. The results presented here extend the work introduced in [24].
The paper is organized as follows: Section 2 presents the definition and some properties of IvFIs and IvFCs. An expression for interval-valued intuitionistic version of the Atanassov's intuitionistic fuzzy index is introduced in Section 3, in order to study properties of IvIFIs, which are generated by idempotent interval-valued aggregation functions and a pair of mutual-dual interval-valued functions: IvFIs and their corresponding coimplications. In Section 4, main results, the ongoing work and final remarks are pointed out.
2 INTERVAL-VALUED FUZZY (CO)IMPLICATIONS
In IvFL, the membership degrees are subintervals of the unit interval U =[0, 1] approximating the correct (but unknown) membership degree [14]. Thus, an interval-valued fuzzy negation  is briefly described in this section founding the study of
is briefly described in this section founding the study of  -dual (co)implications. And, interval aggregation functions and interval-valued fuzzy (co)implications are also presented. For additional information, see [13].
-dual (co)implications. And, interval aggregation functions and interval-valued fuzzy (co)implications are also presented. For additional information, see [13].
Let  ={[x1, x2]|x1, x2 ∈U and 0 < x1< x2< 1}. The projections l
={[x1, x2]|x1, x2 ∈U and 0 < x1< x2< 1}. The projections l , r
, r :
:  → U are defined by l
→ U are defined by l ([x1, x2]) =X1 and r
([x1, x2]) =X1 and r ([x1, x2]) =x2, respectively. For X ∈
([x1, x2]) =x2, respectively. For X ∈  , l
, l (X) and r
(X) and r (X) are also denoted by X and
(X) are also denoted by X and 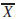 , respectively. For each x ∈U, a degenerate interval [x, x] will be denoted by x and the set of all degenerate intervals will be denoted by
, respectively. For each x ∈U, a degenerate interval [x, x] will be denoted by x and the set of all degenerate intervals will be denoted by  . And, let <
. And, let <  ⊆
⊆  2 be the Kulisch-Miranker (or product) order, such that for all X, Y ∈
2 be the Kulisch-Miranker (or product) order, such that for all X, Y ∈  , is given by 1
1
See in [11], results extending the partial order
<
to a total order.
:
, is given by 1
1
See in [11], results extending the partial order
<
to a total order.
:
Thus, for all X ∈  , X > [0, 0]= 0 and X < [1, 1]= 1. In addition, we also consider
, X > [0, 0]= 0 and X < [1, 1]= 1. In addition, we also consider 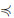
 ⊆
⊆ 2 as the binary relation2
2
Relation
is not an order but its reflexive closure, it is a partial order.
given by:
2 as the binary relation2
2
Relation
is not an order but its reflexive closure, it is a partial order.
given by:

Proposition 1.For all X, Y ∈  , if X
, if X 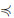
Proof. It follows from Eqs. (2.1) and (2.2).
Remark 1.Proposition 1 states that the partial order< extends the binary relation
extends the binary relation 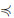
 .
.
For each real function : Un → U, for all  = (X1, X2, ..., Xn) ∈
= (X1, X2, ..., Xn) ∈ nand =
nand = (x1, x2 ..., xn) ∈ Unsuch that xi ∈ Xi for 1 < i < n, the canonical representation of [26] is the interval function
(x1, x2 ..., xn) ∈ Unsuch that xi ∈ Xi for 1 < i < n, the canonical representation of [26] is the interval function  :
:  n →
n →  , defined by
, defined by
The interval function  :
:  n →
n →  is well defined and called the best interval representation of a real function : Un→ U, meaning that for any other interval representation F of , the inclusion F (
is well defined and called the best interval representation of a real function : Un→ U, meaning that for any other interval representation F of , the inclusion F ( ) ⊆ (
) ⊆ ( ) holds.
) holds.
2.1 Interval-valued fuzzy negations and interval aggregations
An interval-valued fuzzy negation (shortly IvFN) is a function  :
:  →
→  which verifies, for all X, Y ∈
which verifies, for all X, Y ∈  , the following two properties:
, the following two properties:
 (0) = 1 and
(0) = 1 and  (1) =0;
2 If X<Y then
(1) =0;
2 If X<Y then  (Y) <
(Y) < (X).
(X).
If  also satisfies the involutive property (
also satisfies the involutive property ( (
( (X)) = X) then
(X)) = X) then  is called a strong IvFN. See, e.g., the Zadeh's IvFN which is given by
is called a strong IvFN. See, e.g., the Zadeh's IvFN which is given by
Notice that, Eq. (2.4) provides a characterization of
S by the canonical representation of NS, when NS(x) =1 - x, which means S =
S = 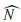 S, by Eq.(2.3). In the following two propositions, some properties related to
S, by Eq.(2.3). In the following two propositions, some properties related to  S are presented, where the sum between X, Y ∈
S are presented, where the sum between X, Y ∈  is defined as X +Y =[X + Y,
is defined as X +Y =[X + Y, 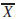 +
+ 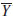 ] ∈
] ∈ .
.
Proposition 2.For all X, Y ∈ , X +Y <
, X +Y <
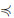 S(Y).
S(Y).
Proof. (⇒) For all X, Y ∈  , X +Y <
, X +Y <
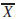 +
+ 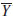 ] < 1. It also means that X + Y < 1 and
] < 1. It also means that X + Y < 1 and 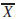 +
+ 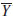 < 1. So it is equivalent to X < NS (Y) =
< 1. So it is equivalent to X < NS (Y) =  S(Y) and
S(Y) and 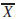 < NS (
< NS (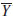 ) =
) = 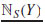 . Therefore we can conclude that X
. Therefore we can conclude that X 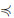
 (Y). (
(Y). ( ) Analogously done.
) Analogously done. 
Corollary 1.For all X, Y ∈ , if X + Y <
, if X + Y <
Proof. Straightforward from the Propositions 1 and 2. 
An interval-valued aggregation 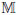 :
:  2 →
2 →  verifies the following properties:
verifies the following properties:
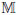 (0, 0) =0 and
(0, 0) =0 and 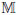 (1, 1) =1 (boundary conditions);
2 If X <Z then
(1, 1) =1 (boundary conditions);
2 If X <Z then 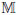 (X, Y) <
(X, Y) <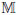 (Z, Y), ∀X, Y, Z ∈
(Z, Y), ∀X, Y, Z ∈ (monotonicity property);
3
(monotonicity property);
3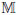 (X, Y ) =M(Y, X), ∀X, Y ∈
(X, Y ) =M(Y, X), ∀X, Y ∈  (commutativity property).
(commutativity property).
Additionally, an idempotent IvA function is an IvA also verifying
4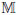 (X, X) = X, ∀X ∈
(X, X) = X, ∀X ∈ (idempotency property).
(idempotency property).
Remark 2.Consider ∨, ∧:  2 → U, ∨(x, y) = max{x, y} and ∧(x, y) = min{x, y} and their related interval extensions,
2 → U, ∨(x, y) = max{x, y} and ∧(x, y) = min{x, y} and their related interval extensions,  ,
,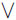 :
:
 , which are idempotent IvAs given by:
, which are idempotent IvAs given by:
By the product order, for each IvA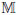 ,
,  (X, Y ) <
(X, Y ) <
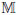 (X, Y ) <
(X, Y ) <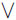 (X, Y ), ∀X, Y ∈
(X, Y ), ∀X, Y ∈ . And, the canonical representation of an aggregation M : U2 → U is characterized as:
. And, the canonical representation of an aggregation M : U2 → U is characterized as:
according to [14, Definition 4.3.].
2.2 Interval-valued fuzzy (co)implications
In thispaper, thedefinitionofan IvF(C)Iis the following one, which is equivalent to the definition proposed by Kitainik [18] (see also Fodor and Roubens [15]). Such definition extends the one presented in [7, Definition 3], reproducing fuzzy (co)implications when degenerate intervals are considered.
Definition 1. [13, Definition 6] An IvF(C)I operator (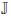 )
) :
: 2 →
2 → fulfills, for all X, Y, Z ∈
fulfills, for all X, Y, Z ∈ , the boundary condition stated by
, the boundary condition stated by
 (1, 0) = 0;
(1, 0) = 0; 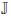 0:
0: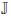 (0, 1) =1;
(0, 1) =1;
together with the following additional properties:
1 X<Z ⇒ (X, Y) >
(X, Y) > (Z, Y);
(Z, Y); 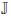 1: X <Z ⇒
1: X <Z ⇒ 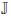 (X, Y) <
(X, Y) <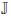 (Z, Y);
2 Y<Z ⇒
(Z, Y);
2 Y<Z ⇒  (X, Y) <
(X, Y) < (X, Z);
(X, Z); 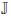 2: Y <Z ⇒
2: Y <Z ⇒ 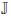 (X, Y) >
(X, Y) >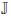 (X, Z);
3
(X, Z);
3 (0, Y) = 1;
(0, Y) = 1; 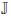 3:
3: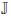 (1, Y) = 0;
4
(1, Y) = 0;
4 (X, 1) = 1;
(X, 1) = 1; 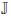 4:
4: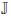 (X, 0) =0.
(X, 0) =0.
Proposition 3.[23, Proposition 3.4] A function
 (
(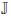
 ) :
) :  2 →
2 → is an IvF(C)I operator if and only if there exists an IvF(I)C operator
is an IvF(C)I operator if and only if there exists an IvF(I)C operator  (
(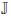 ) :
) :  2 →
2 →  and an IvFN
and an IvFN  :
:  →
→  such that, ∀X, Y ∈
such that, ∀X, Y ∈ , the next equality holds:
, the next equality holds:
 (X, Y ) =
(X, Y ) =  (
( (
( (X),
(X),  (Y ))), (
(Y ))), (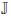
 (X, Y ) =
(X, Y ) =  (
(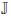 (
( (X),
(X),  (Y )))) .
(Y )))) .
When  is an involutive interval-valued negation, (
is an involutive interval-valued negation, ( ,
, 
 ) is said to be a pair of mutual
) is said to be a pair of mutual  -dual interval functions. In the following, IvF(C)Is are characterized as the canonical representability [26] of fuzzy (co)implications.
-dual interval functions. In the following, IvF(C)Is are characterized as the canonical representability [26] of fuzzy (co)implications.
Proposition 4.[21, Proposition 6][5, Proposition 10] A function (
( ), called canonical representation of I (J) :U2 →U, is given as
), called canonical representation of I (J) :U2 →U, is given as
3 INTERVAL-VALUED INTUITIONISTIC FUZZY IMPLICATIONS
As a generalization of an IFS, an interval-valued intuitionistic fuzzy set (shortly IvIFS) is given as
A ={(x, MA(x), NA(x))|x ∈X, MA(x) +NA(x) <
1},where NA(x) is the interval degree of non-membership of x in set A, which is less, at most equal to the complement of the related interval degree of membership MA(x), and therefore does not necessarily equal to one.
The set  ={
={ = (X1, X2) ∈
= (X1, X2) ∈  2|X1 +X2<
2|X1 +X2<
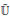 , r
, r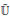 : →
: →  , which are defined by l
, which are defined by l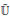 (
( ) =l
) =l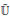 (X1, X2) = X1 and r
(X1, X2) = X1 and r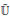 (
( ) =r
) =r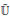 (X1, X2) =X2, respectively. According to [10], we also consider the binary relations in
(X1, X2) =X2, respectively. According to [10], we also consider the binary relations in  :
:
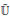 1 :
1 : <
<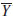 ⇔X1<Y1 and X2>Y2; or
⇔X1<Y1 and X2>Y2; or
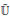 2 :
2 :
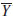 ⇔X1<Y1 and X2>Y2; or
⇔X1<Y1 and X2>Y2; or
also 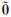 = (0, 1) <
= (0, 1) <
 and
and 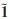 =(1, 0) >
=(1, 0) > , for all
, for all  ,
,  ∈
∈ .
.
Additionally, let 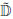 ={
={ =(X1, X2)|X1 +X2 =1} ⊆
=(X1, X2)|X1 +X2 =1} ⊆ be the set of diagonal elements on
be the set of diagonal elements on  defined by pairs of complementary degenerate intervals.
defined by pairs of complementary degenerate intervals.
3.1 Interval intuitionistic fuzzy index
Consider χ as an ordinary finite non-empty set. Let MA and NA be the interval-valued degrees of membership and non-membership related to an element x ∈ χ in an IvIFS A. A function ΠA: χ → , called an interval intuitionistic fuzzy index (IvIFIx) of an element x in an IvIFS A, is given as
, called an interval intuitionistic fuzzy index (IvIFIx) of an element x in an IvIFS A, is given as
Thus, it follows that ΠA(x) <  S(MA(x)) =
S(MA(x)) = 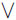 (
(
 = (MA(x), NA (x) = (X1, X2) ∈
= (MA(x), NA (x) = (X1, X2) ∈  , we denote ΠA (x) by Π
, we denote ΠA (x) by Π . Thus, Eq. (3.1) can be expressed as Π
. Thus, Eq. (3.1) can be expressed as Π =
= S (X1 +X2), with 0 <
S (X1 +X2), with 0 < Π
Π <1.
<1.
Proposition 5.The IvIFIx of =(X1, X2) ∈
=(X1, X2) ∈ can be expressed as:
can be expressed as:
Proof. When  = (X1, X2), by Eqs. (2.4) and (3.1), Π
= (X1, X2), by Eqs. (2.4) and (3.1), Π =
=  S(X1 +X2).Then Π
S(X1 +X2).Then Π =
= and Eq. (3.2) is verified.
and Eq. (3.2) is verified.
Proposition 6.Consider ={(x1, x2) ∈U2 | x1< NS(x2)} and π
={(x1, x2) ∈U2 | x1< NS(x2)} and π as the intuitionistic fuzzy index of
as the intuitionistic fuzzy index of  = (x1, x2) ∈
= (x1, x2) ∈  given by π
given by π =
=  S(x1 +x2) (see [7, Section 1.2]). Then, for all
S(x1 +x2) (see [7, Section 1.2]). Then, for all  (X1, X2) ∈
(X1, X2) ∈ , Π
, Π is given as Π
is given as Π =
=  .
.
Proof. Since X1 +X2<
1, we obtain both inequalities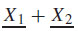 < 1 and
< 1 and 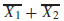 < 1. Then we have that (
< 1. Then we have that (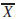 1,
1, 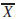 2), (X 1, X2) ∈
2), (X 1, X2) ∈ . Moreover, these imply that Π(x1, x2)=
. Moreover, these imply that Π(x1, x2)=  S(X1 + X2) =[NS
S(X1 + X2) =[NS 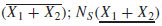 )]. Therefore, the expression Π(x1, x2) =[NS(
)]. Therefore, the expression Π(x1, x2) =[NS(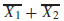 ), NS(
), NS(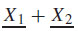 )]=[π
)]=[π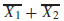 , π(
, π(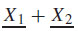 )] is obtained.
)] is obtained.
Definition 2.An IvIFI I :
I :  2 →
2 →  is a function satisfying the boundary condition
is a function satisfying the boundary condition  I (
I (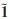 ,
,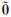 )=
)=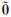 and, for all
and, for all ,
,  ,
, 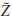 ∈
∈ , the following properties hold:
, the following properties hold:
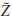 ⇒
⇒ I (
I ( ,
,  ) >I (
) >I (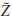 ,
,  ) (right antitonicity property);
I2 <
) (right antitonicity property);
I2 <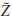 ⇒
⇒ I (
I ( ,
,  ) >I (
) >I ( ,
, 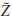 ) (left isotonicity property);
I3
) (left isotonicity property);
I3 I (
I (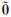 ,
, ) =
) = 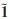 (falsity principle);
I4
(falsity principle);
I4 I (
I ( ,
,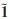 ) =
) = 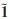 (neutrality principle).
(neutrality principle).
Definition 3.An IvIFI I :
I : 2 →
2 → is called a diagonal preserving IvIFI if, for all
is called a diagonal preserving IvIFI if, for all  ,
,  ∈
∈ 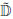 , it verifies the additional property:
, it verifies the additional property:
Lemma 1. Π = 0 if and only if
= 0 if and only if  ∈
∈ 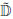 .
.
Proof. Π = 0 ⇔ NS(X1 +X2) = 0. So, we have Π
= 0 ⇔ NS(X1 +X2) = 0. So, we have Π = 1 -(X1 +X2) = 0 ⇔[1 -
= 1 -(X1 +X2) = 0 ⇔[1 -  = 0. In addition, it also means that Π
= 0. In addition, it also means that Π =
= =1 and
=1 and  = 1 ⇔
= 1 ⇔
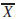 2) and
2) and 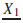 =NS(
=NS(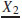 ). Therefore, Π
). Therefore, Π =
= ∈
∈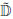 .
. 
Proposition 7.An IvIFI operator I :
I : 2 →
2 → is a diagonal preserving operator if and only if
is a diagonal preserving operator if and only if  I (
I ( ,
,  ) ∈
) ∈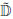 when
when  ,
,  ∈
∈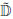 ⊆
⊆ .
.
Proof. (⇒)If  I is diagonal preserving IvIFI then by Definition 3, Π
I is diagonal preserving IvIFI then by Definition 3, Π (
( ,
,  ) = 0 when
) = 0 when  ,
,  ∈
∈  . Therefore, by Lemma 1,
. Therefore, by Lemma 1,  I (
I ( ,
,  ) ∈
) ∈  . (
. ( ) Let
) Let  ,
,  ∈
∈  . If
. If  I (
I ( ,
,  ) ∈
) ∈ 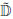 , then there exists
, then there exists 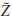 =(Z1, Z2) ∈
=(Z1, Z2) ∈ 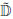 , which means that Z2 =1 -Z1, such that
, which means that Z2 =1 -Z1, such that  I (
I ( ,
,  ) =
) = 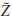 . Therefore, Π
. Therefore, Π (
( ,
,  ) = Π
) = Π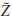 = NS(Z1 +Z2) =
= NS(Z1 +Z2) =  S(1) = 0. Hence, Π
S(1) = 0. Hence, Π (
( ,
,  ) = 0 and, we conclude, by Lemma 1,
) = 0 and, we conclude, by Lemma 1,  I is a diagonal preserving IvIFI.
I is a diagonal preserving IvIFI. 
3.2 IvIFIs generated from IvAs, IvFIs and IvFCs operators
Based on [7, Proposition 3], we present an expression for an interval intuitionistic fuzzy implication II generated by a finite set of interval aggregation functions Mi and a pair of interval mutually dual functions ( ,
,  N). Such pair consists of an IvFI operator
N). Such pair consists of an IvFI operator  and its corresponding IvIFC operator
and its corresponding IvIFC operator  N , obtained by a strong IvFN
N , obtained by a strong IvFN  .
.
Definition 4.Let be an IvFI,
be an IvFI,
 S-dual construction, and M ={
S-dual construction, and M ={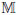 i :
i :  2 →
2 →  |i ∈{1, 2, 3, 4}} be a family of idempotent IvA verifying the next conditions:
|i ∈{1, 2, 3, 4}} be a family of idempotent IvA verifying the next conditions:
For all = (X1, X2),
= (X1, X2),  = (Y1, Y2) ∈
= (Y1, Y2) ∈  ,
,  I :
I :  2 →
2 →  is defined by the projection-functions as:
is defined by the projection-functions as:
Theorem 1.The binary function I :
I :  2 →
2 →  given in Definition 4 is an IvIFI operator.
given in Definition 4 is an IvIFI operator.
Proof. It is immediate that  I is well defined, satisfying the boundary conditions:
I is well defined, satisfying the boundary conditions:
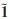 ,
, 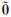 ) (
) ( (
( 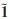 ,
, 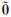 ),
),  (0, 1)) (0, 1) =
(0, 1)) (0, 1) = 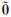 .
.
For all  ,
,  and
and 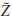 ∈
∈ , we have that
, we have that
[
I 1]Assuming that
<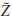 , which means X1< Z1 and X2> Z2 and equivalently, N(X2) < N(Z2). Thus, by the isotonic functions
, which means X1< Z1 and X2> Z2 and equivalently, N(X2) < N(Z2). Thus, by the isotonic functions 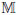 1 and
1 and 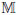 3, both inequations are verified:
3, both inequations are verified: 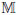 1(X1, NS(X2)) <1(Z1, NS(Z2)) and
1(X1, NS(X2)) <1(Z1, NS(Z2)) and 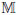 3(NS (X1), X2) >3(NS(Z1), Z2).So, for Definition 1, the inequations related to
3(NS (X1), X2) >3(NS(Z1), Z2).So, for Definition 1, the inequations related to  I -projections are given as:
I -projections are given as:
Therefore,
I verifies the first place antitonicity.[
I 2]Assuming that
<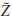 . By the isotonicity of
. By the isotonicity of 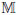 2 and
2 and 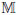 4, we have the following:
4, we have the following:
 and
and

For Definition 1, we have that:
Therefore,
I verifies the second place isotonicity.[
I 3]By Definition 1,  and
and 
 fulfills
fulfills  3 and
3 and 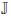 3, respectively. Then the projections hold:
3, respectively. Then the projections hold:
Therefore
I (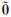 , Y) =
, Y) = 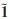 .
.
[
I 4]By Definition 1,  and
and 
 fulfills
fulfills  4 and
4 and 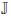 4, respectively. Then the projections hold:
4, respectively. Then the projections hold:
[
I 5]If X1= S(X2) and Y1 =
S(X2) and Y1 = S(Y2) then we have the following:
S(Y2) then we have the following:
Therefore, Π
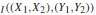 = 0
= 0
3.3 Extending fuzzy implications from IvFL to IvIFL
See, in Table 1, some examples of intuitionistic fuzzy implication (shortly IFI) II which are generated by action of aggregators in Mi , with i ∈ {1, 2, 3, 4}, such that M1 = M3 =∨and M2 = M4 =∧, as presented in [19]. For details see [19] and [3]. In Table 2 we present the corresponding generalized IvIFIs ( I ), based on Definition 4.
I ), based on Definition 4.
In the following example, an interval-valued extension the of Łukasiewicz's implication is considered according to Definition 4. It is obtained based on the Łukasiewicz's implication and its NS-dual coimplication.
Example 1.For i ∈{1, 2, 3, 4}, let 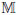 i :
i : 2 →
2 →  be idempotent IvA operator given by:
be idempotent IvA operator given by:
It is clear, by Definition 4, for each i ∈{1, 2, 3, 4}, 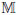 i satisfies the conditions stated by Eqs. (3.3) and (3.4), assuring that, by Theorem 1, IvIFIs can be generated by IvAs and pairs of implications and coimplications.
i satisfies the conditions stated by Eqs. (3.3) and (3.4), assuring that, by Theorem 1, IvIFIs can be generated by IvAs and pairs of implications and coimplications.
Let ( LK,
LK, 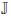 LK )be the pair of
LK )be the pair of  S-dual functions given as:
S-dual functions given as:
By Theorem 1, the ILK -projections are given as:
ILK -projections are given as:  (
( ,
,  ) = ∧ (1, X2 +Y1); and
) = ∧ (1, X2 +Y1); and  (
( ,
,  ) =
) = 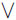 (0, Y2 -
(0, Y2 - S(X1)). So,
S(X1)). So,  is a natural interval extension of
is a natural interval extension of  (
( ,
,  ) = ∧ (1, (x2+ y1)), ∨(0, (X1 +Y2-1)) as seen in the first lines of Tables 1 and 2. Its dual construction can be analogously obtained. The other IvIFIs of Table 1 can be analogously constructed, see these in Table 2.
) = ∧ (1, (x2+ y1)), ∨(0, (X1 +Y2-1)) as seen in the first lines of Tables 1 and 2. Its dual construction can be analogously obtained. The other IvIFIs of Table 1 can be analogously constructed, see these in Table 2.
Table 3 reports the index expression related to IvIFIs presented in Table 2. See, for instance, the respective expressions of the fuzzy index of  and
and  as follows:
as follows:
And, the interval expressions of these fuzzy indexes, which were obtained by considering the corresponding IvIFIs, as presented in the two first lines in Table 3:
The other indexes can be analogously obtained.
Now, based on the canonical representability, we present the condition under which an IvIFI is representable. For that, let II be an IFI generated by a set of idempotent aggregations Mi , for i ∈{1, 2, 3, 4}, together with an implication I and its corresponding intuitionistic fuzzy coimplication (IFC) IN , based on [7, Proposition 3].
Proposition 8.Consider I :
I :  2 →
2 → an IvIFI given as in Definition 4 by the following representable fuzzy connectives:
an IvIFI given as in Definition 4 by the following representable fuzzy connectives: 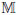 i =
i =  i for i ∈ {1, 2, 3, 4} and where each Mi is an aggregation function;
i for i ∈ {1, 2, 3, 4} and where each Mi is an aggregation function;  =
=  and
and  N =
N =  Nwhenever (I, IN )is a pair of NS-dual functions given as a fuzzy implication and its corresponding fuzzy coimplication. For all
Nwhenever (I, IN )is a pair of NS-dual functions given as a fuzzy implication and its corresponding fuzzy coimplication. For all  =(X1, X2),
=(X1, X2),  =(Y1, Y2) ∈
=(Y1, Y2) ∈ ,
,  I can be characterized as:
I can be characterized as:
when II :  2 →
2 →  is the IFI obtained from Mi and the pair (I, IN ), see [7, Section 3.2].
is the IFI obtained from Mi and the pair (I, IN ), see [7, Section 3.2].
Proof. Firstly, let  =(X1, X2),
=(X1, X2),  =(Y1, Y2) ∈
=(Y1, Y2) ∈ . Then,
. Then, 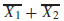 <1 and therefore
<1 and therefore 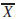 1 +
1 + 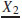 <1 which means (
<1 which means (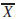 1,
1, 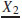 ) ∈
) ∈  . Analogously,
. Analogously,  , (
, (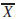 1,
1, 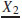 ),
),  ∈
∈ . Now, by Definition 4, it follows that:
. Now, by Definition 4, it follows that:
Therefore, we conclude that Eq. (3.7) is held. Analogously, Eq. (3.8) is proved.
In the following, Corollary 2 presents the conditions under which projection functions over pairs of degenerate intervals are preserved by an IvIFI
I , as given in Definition 4.Corollary 2.Under the conditions of Proposition 8, the IvIFI operator I :
I : 2 →
2 → is a diagonal preserving operator.
is a diagonal preserving operator.
Proof. By Proposition 7, it is sufficient to show that, for all  ,
,  ∈
∈ 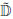 it holds that
it holds that  I (
I ( ,
,  ) ∈
) ∈ 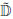 . By Proposition 8, it follows that
. By Proposition 8, it follows that  I (
I ( ,
,  ) =
) = I ((X1, X2), (Y1, Y2)) =(
I ((X1, X2), (Y1, Y2)) =( (X1, Y1),
(X1, Y1), 
 (X2, Y2)). So, in accordance with the characterization stated by Eqs. (3.7) and (3.8), we have the equations:
(X2, Y2)). So, in accordance with the characterization stated by Eqs. (3.7) and (3.8), we have the equations:
Since,  ,
,  ∈
∈ 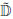 , then
, then 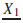 =
=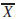 1,
1, 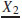 =
= 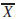 2,
2,  =
= 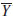 1 and
1 and  =
= 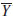 2. Therefore both are degenerate intervals. In addition, since (
2. Therefore both are degenerate intervals. In addition, since ( ,
, 
 ) is a pair of
) is a pair of  S-dual functions, we have that
S-dual functions, we have that 
 (X2, Y2) =
(X2, Y2) =  S(
S( (
( S(X2),
S(X2),  S(Y2))) =
S(Y2))) = S(
S( (X1, Y1)). Therefore,
(X1, Y1)). Therefore,  (X1, Y1) +
(X1, Y1) +
 (X2, Y2) = 1, concluding that
(X2, Y2) = 1, concluding that  I (
I ( ,
,  ) ∈
) ∈ 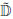 .
. 
3.4 Properties of IvIFIs
An IvIFI operator can be demanded to verify other properties which are inherited when the fuzzy implication is generalized to the intuitionistic fuzzy case, see [7, 12] and [13]. In such context, we consider the next truly intuitionistic fuzzy properties:
Proposition 9.Let I :
I :  2 →
2 →  be an IvIFI operator whose projections are given by Eqs. (3.5) and (3.6). Therefore
be an IvIFI operator whose projections are given by Eqs. (3.5) and (3.6). Therefore  I verifies
I verifies
 I7.
I7.
Proof. Let 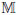 i∈{1, 2, 3, 4} be an idempotent IvA operators. Then, if follows that:
i∈{1, 2, 3, 4} be an idempotent IvA operators. Then, if follows that:
By
I1 and I2, we have that: (i)
I2, we have that: (i) 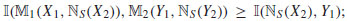 and (ii)
and (ii) 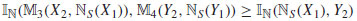 . So, I is well defined.
. So, I is well defined.
[
I6]By (i) and (ii),
I ( ,
,  ) +
) +  I (
I ( ,
,  ) >
) >  (
( S (X2), Y1) +
S (X2), Y1) + 
 (
( S (X1), Y2) and we have:
S (X1), Y2) and we have: 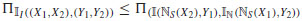 . Then, I6 is verified.
. Then, I6 is verified.
[
I7]Based on (i) and (ii),
I ((X1, X2), (Y1, Y2))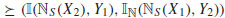 . So, it means that I satisfies
. So, it means that I satisfies  I 7.
I 7.
Therefore, Proposition 9 holds.
Proposition 10.Let I be an IvIFI operator whose projections are given by Eqs. (3.5), (3.6). When
I be an IvIFI operator whose projections are given by Eqs. (3.5), (3.6). When  (X, Y ) >
(X, Y ) >  (X, Y )
(X, Y )  I verifies
I verifies  I 8.
I 8.
Proof. For all  ,
,  ∈
∈  , the following holds.
, the following holds.
By hypothesis  (X, Y ) > (X, Y ) and then l
(X, Y ) > (X, Y ) and then l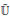 (
( I (
I ( ,
,  )) + r
)) + r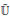 (
( I)(
I)( ,
,  )) >
)) >  (X1, Y1). Moreover, it holds that
(X1, Y1). Moreover, it holds that
Therefore,  , meaning that
, meaning that
 I 8.
I 8. 
Proposition 11.Let I be an IvIFI operator whose projections are given by Eqs. (3.5), (3.6). If
I be an IvIFI operator whose projections are given by Eqs. (3.5), (3.6). If I verifies
I verifies I 9 then also verifies
I 9 then also verifies  I 10.
I 10.
Proof. Straightforward. 
4 CONCLUSION
IvIFL and IFL have been studied as a natural generalization of FL taking into account: (i) in the interval approach, the uncertainty due to the lack of information in the definition of a membership function; and (ii) in the intuitionistic approach, the non-complementary idea of the dual construction of membership functions.
Thus, it seems interesting to move on to another challenging approach such as IvIFL integrating both approaches. So, this work studies IvIFIs in the sense of [28] and provides interpretation for interval-valued intuitionistic fuzzy index. It has shown that the IvFIs obtained by action of canonical representation of aggregation functions and mutual dual functions also extends the work introduced by [7].
Further work considers applying the generalization introduced in Theorem 1 in order to analyse the main classes of IvIFIs and other constructions based on interval automorphisms, based on our previous works [5, 21, 22] and [23].
ACKNOWLEDGMENTS
This work is supported by the Brazilian funding agencies CNPq (Ed. PQ and Universal, under the process numbers 307681/2012-2 and 480832/2011-0, respectively) and FAPERGS (Ed. PqG 06/2010, under the process number 11/1520-1). The authors are grateful to the referees for their valuable suggestions.
REFERENCES
[1] K. Atanassov & G. Gargov. Interval valued intuitionistic fuzzy sets. Fuzzy Sets and Systems, 31(3)(1989),343-349.
[2] K.T. Atanassov. Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1986),87-96.
[3] M. Baczyński & B. Jayaram. QL-implications: Some properties and intersections. Fuzzy Sets and Systems, 161(2)(2008),158-188.
[4] B. Bedregal, G. Beliakov, H. Bustince, T. Calvo, R. Mesiar & D. Paternain. A class of fuzzy multisets with a fixed number of memberships. Information Sciences, 189(1)(2012),1-17.
[5] B. Bedregal, G. Dimuro, R. Santiago & R. Reiser. On interval fuzzy S-implications. Information Sciences, 180(8)(2010),1373-1389.
[6] P. Burillo & H. Bustince. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets and Systems, 79(1996),403-405.
[7] H. Bustince, E. Barrenechea & V. Mohedano. Intuicionistic fuzzy implication operators - an expression and main properties. Int.l J. of Uncertainty, Fuzziness and Knowledge-Based Systems, 12(3)(2004),387-406.
[8] H. Bustince, E. Barrenechea & M. Pagola. Generation of interval-valued fuzzy and Atanassov's intuitionistic fuzzy connectives from fuzzy connectives and from Kfonte symboloperators: Laws for conjunctions and disjunctions, amplitude. Int. J. Intell. Syst, 23(6)(2008),680-714.
[9] H. Bustince, E. Barrenechea & M. Pagola. Relationship between restricted dissimilarity functions, restricted equivalence functions and normal en-functions: Image thresholding invariant. Pattern Recognition Letters, 29(2008),525-536.
[10] H. Bustince, P. Burillo & F. Soria. Automorphism, negations and implication operators. Fuzzy Sets and Systems, 134(2)(2003),209-229.
[11] H. Bustince, J. Fernandez, A. Kolesárová & R. Mesiar. Generation of linear orders for intervals by means of aggregation functions. Fuzzy Sets and Systems, 220(2013),69-77.
[12] C. Cornelis, G. Deschrijver & E.E. Kerre. Advances and challenges in interval-valued fuzzy logic. Fuzzy Sets and Systems, 157(5)(2006),622-627.
[13] G. Cornelis, G.Deschrijver & E. E.Kerre. Implication in intuitionistic fuzzy and interval-valued fuzzy set theory: construction, classification, application. Intl. J. of Approximate Reasoning, 35(1)(2004), 55-95.
[14] G. Deschrijver & E.E. Kerre. Implicators based on binary aggregation operators in interval-valued fuzzy set theory. Fuzzy Sets and Systems, 153(2)(2005),229-248.
[15] J. Fodor & M. Roubens. Fuzzy Preference Modelling and Multicriteria Decision Support. Kluwer Academic Publisher, Dordrecht, (1994).
[16] W. Gau & D. Buehrer. Vague sets. IEEE Trans. Systs.Man Cybernet, 23(2)(1993),610-614.
[17] A. Jurio, M. Pagola, R. Mesiar & H. Bustince. Image magnification using interval information. IEEE Transactions on Image Processing, 20(11)(2011),3112-3123.
[18] L. Kitainik. Fuzzy Decision Procedures with Binary Relations: Towards a Unified Theory. Kluwer Academic Publishers, (1993). [19] L. Lin & Z. Xia. Intuitionistic fuzzy implication operators: Expressions and properties. Journal of Applied Mathematics and Computing, 22(3)(2003),325-338.
[20] A. Piskunov. Fuzzy implication in fuzzy systems control. Fuzzy Sets and Systems, 45(1)(1992),25-35.
[21] R.H.S. Reiser & B. Bedregal. Obtaining representable coimplications from aggregation operators and dual operators. In Advances in Intelligent Systems Research - Proceedings of EUSFLAT 2011 and LFA 2011, pages 238-245,Aix-les-Bains, 2011. Paris: Atlantis Press.
[22] R.H.S. Reiser & B. Bedregal. Interval-valued intuitionistic fuzzy implications - construction, properties and representability. Information Science, 248(1)(2013),68-88.
[23] R.H.S. Reiser, B. Bedregal & G.A.A. dos Reis. Interval-valued fuzzy coimplications. Journal of Computer and System Sciences, (2013). DOI: 10.1007/s40314.013.0029.3.
[24] R.H.S. Reiser, B. Bedregal & L. Visintin. Interval-valued intuitionistic fuzzy implications: index, expressions and properties. In Proc. of the XXXIII CNMAC, pages 303-305, Águas de Lindóia, (2012). SBMAC Press.
[25] R. Sambuc. Fonctions φ-floues. Application l'aide au diagnostic en pathologie thyroidienne. PhD thesis, Univ. Marseille, Marseille, (1975).
[26] R.H.N. Santiago, B. Bedregal & B.M. Acióly. Formal aspects of correctness and optimality in interval computations. Formal Aspects of Computing, 18(2)(2006),231-243.
[27] V. Torra. Element selection for intuitionistic fuzzy sets. IJKESDP, 2(2)(2010),160-168.
[28] L. Visintin, R.H.S. Reiser & B. Bedregal. Interval-valued intuitionistic fuzzy implications. In IEEE Conference Publications 2011: Workshop-School on Theoretical Computer Sciences (WEIT), pages 46-52, Pelotas, (2011).
[29] L.A. Zadeh. The concept of a linguistic variable and its application to approximate reasoning - I. Information Sciences, 8(3)(1975),199-249.
Received on November 1, 2012
Accepted on August 26, 2013
- [1] K. Atanassov & G. Gargov. Interval valued intuitionistic fuzzy sets. Fuzzy Sets and Systems, 31(3)(1989),343-349.
- [2] K.T. Atanassov. Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1986),87-96.
- [3] M. Baczyński & B. Jayaram. QL-implications: Some properties and intersections. Fuzzy Sets and Systems, 161(2)(2008),158-188.
- [4] B. Bedregal, G. Beliakov, H. Bustince, T. Calvo, R. Mesiar & D. Paternain. A class of fuzzy multisets with a fixed number of memberships. Information Sciences, 189(1)(2012),1-17.
- [5] B. Bedregal, G. Dimuro, R. Santiago & R. Reiser. On interval fuzzy S-implications. Information Sciences, 180(8)(2010),1373-1389.
- [6] P. Burillo & H. Bustince. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets and Systems, 79(1996),403-405.
- [7] H. Bustince, E. Barrenechea & V. Mohedano. Intuicionistic fuzzy implication operators - an expression and main properties. Int.l J. of Uncertainty, Fuzziness and Knowledge-Based Systems, 12(3)(2004),387-406.
- [8] H. Bustince, E. Barrenechea & M. Pagola. Generation of interval-valued fuzzy and Atanassov's intuitionistic fuzzy connectives from fuzzy connectives and from Kfonte symboloperators: Laws for conjunctions and disjunctions, amplitude. Int. J. Intell. Syst, 23(6)(2008),680-714.
- [9] H. Bustince, E. Barrenechea & M. Pagola. Relationship between restricted dissimilarity functions, restricted equivalence functions and normal en-functions: Image thresholding invariant. Pattern Recognition Letters, 29(2008),525-536.
- [10] H. Bustince, P. Burillo & F. Soria. Automorphism, negations and implication operators. Fuzzy Sets and Systems, 134(2)(2003),209-229.
- [11] H. Bustince, J. Fernandez, A. Kolesárová & R. Mesiar. Generation of linear orders for intervals by means of aggregation functions. Fuzzy Sets and Systems, 220(2013),69-77.
- [12] C. Cornelis, G. Deschrijver & E.E. Kerre. Advances and challenges in interval-valued fuzzy logic. Fuzzy Sets and Systems, 157(5)(2006),622-627.
- [13] G. Cornelis, G.Deschrijver & E. E.Kerre. Implication in intuitionistic fuzzy and interval-valued fuzzy set theory: construction, classification, application. Intl. J. of Approximate Reasoning, 35(1)(2004), 55-95.
- [14] G. Deschrijver & E.E. Kerre. Implicators based on binary aggregation operators in interval-valued fuzzy set theory. Fuzzy Sets and Systems, 153(2)(2005),229-248.
- [15] J. Fodor & M. Roubens. Fuzzy Preference Modelling and Multicriteria Decision Support Kluwer Academic Publisher, Dordrecht, (1994).
- [16] W. Gau & D. Buehrer. Vague sets. IEEE Trans. Systs.Man Cybernet, 23(2)(1993),610-614.
- [17] A. Jurio, M. Pagola, R. Mesiar & H. Bustince. Image magnification using interval information. IEEE Transactions on Image Processing, 20(11)(2011),3112-3123.
- [18] L. Kitainik. Fuzzy Decision Procedures with Binary Relations: Towards a Unified Theory Kluwer Academic Publishers, (1993).
- [19] L. Lin & Z. Xia. Intuitionistic fuzzy implication operators: Expressions and properties. Journal of Applied Mathematics and Computing, 22(3)(2003),325-338.
- [20] A. Piskunov. Fuzzy implication in fuzzy systems control. Fuzzy Sets and Systems, 45(1)(1992),25-35.
- [21] R.H.S. Reiser & B. Bedregal. Obtaining representable coimplications from aggregation operators and dual operators. In Advances in Intelligent Systems Research - Proceedings of EUSFLAT 2011 and LFA 2011, pages 238-245,Aix-les-Bains, 2011. Paris: Atlantis Press.
- [22] R.H.S. Reiser & B. Bedregal. Interval-valued intuitionistic fuzzy implications - construction, properties and representability. Information Science, 248(1)(2013),68-88.
- [23] R.H.S. Reiser, B. Bedregal & G.A.A. dos Reis. Interval-valued fuzzy coimplications. Journal of Computer and System Sciences, (2013). DOI: 10.1007/s40314.013.0029.3.
- [24] R.H.S. Reiser, B. Bedregal & L. Visintin. Interval-valued intuitionistic fuzzy implications: index, expressions and properties. In Proc. of the XXXIII CNMAC, pages 303-305, Águas de Lindóia, (2012). SBMAC Press.
- [25] R. Sambuc. Fonctions φ-floues. Application l'aide au diagnostic en pathologie thyroidienne PhD thesis, Univ. Marseille, Marseille, (1975).
- [26] R.H.N. Santiago, B. Bedregal & B.M. Acióly. Formal aspects of correctness and optimality in interval computations. Formal Aspects of Computing, 18(2)(2006),231-243.
- [27] V. Torra. Element selection for intuitionistic fuzzy sets. IJKESDP, 2(2)(2010),160-168.
- [28] L. Visintin, R.H.S. Reiser & B. Bedregal. Interval-valued intuitionistic fuzzy implications. In IEEE Conference Publications 2011: Workshop-School on Theoretical Computer Sciences (WEIT), pages 46-52, Pelotas, (2011).
- [29] L.A. Zadeh. The concept of a linguistic variable and its application to approximate reasoning - I. Information Sciences, 8(3)(1975),199-249.
 to a total order.
to a total order. 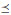 is not an order but its reflexive closure, it is a partial order.
is not an order but its reflexive closure, it is a partial order.Publication Dates
-
Publication in this collection
11 Oct 2013 -
Date of issue
Aug 2013
History
-
Received
01 Nov 2012 -
Accepted
26 Aug 2013





























 .
.


