Multi-fractal Analysis for Riemann Serie and Mandelbrot Binomial Measure with (min,+)-Wavelets

ABSTRACT

One introduces first the so-called (min, +)-wavelets which are lower and upper hulls build from (min, +) analysis in order to perform multi-fractal analysis. In a second step it is applied to functions such as the Riemann serie and binomial Mandelbrot measure for numerical computations of their singularities spectrum, and comparisons with well-known theoretical and to WTMM method results.

Keywords:
(min, +)-wavelets; fractal and multi-fractal analysis; Hölder exponent; scaling function; singularities spectrum

RESUMO

Em primeiro lugar, introduz-se os chamados (min, +)-wavelets que são limitantes inferior e superior construídos para análise (min, +), utilizados em análise multi-fractal.Em segundo lugar, esta análise é aplicada a funções tais como série de Riemann e medida binomial de Mandelbrot, para o cálculo numérico do espectro de singularidades, e comparações com a teoria bem conhecida e com resultados do método WTMM.

Palavras-chave:
(min, +)-wavelets; análise fractal e multi-fractal; expoente de Hölder,funções de escala; espectro de singularidades

1 INTRODUCTION

In the end of the 19^th and in the beginning of the 20^th centuries, many mathematicians studied the behaviour of functions which are continuous everywhere and nowhere differentiable such as Weierstrass functions ⁴³, or brownian motions ¹⁸ for instance. Their common features is to be irregular in the same way everywhere. Those properties have been formalised by Mandelbrot within the fractal theory.

Before him, Kolmogorov ^21),(22, Kadanoff ^19),(24 and others have already builded models and theories to explain some phenomena in physics exhibiting such kind of irregularities with scale invariant properties ²⁰. Particularly, Kolmogorov modelled in his famous K41's theory, small fluctuations of flow spatial velocity field v between two points x and x + l in a domain Ω ⊂ ℝ³ expressed in L^q norm, q ∊ ℕ*, with fractional Brownian motion and Hurst exponent H ∊ ℝ⁺*:

(1.1)

and he found that the scaling function ξv behaves as ξv(q) = Hq with H = 1/3 when||I|| → 0, where ||·|| is the euclidian ℝ³-norm.

Some recent experiments have exhibited the so-called intermittency phenomenon which ischaractherised by the fact that ξv is much more complex than in K41's theory, and exhibits particular properties such as concavity ¹⁴. In fluid turbulence, intermittency is defined as the existence of observed strong fluctuations at small scales, it causes the deviation to the turbulence statistics due to the Kolmogorov prediction ²¹ which mainly relies on self-similarity. The first generalization of self-similarity as "refined similarity hypothesis" to account for possible non Gaussianity of the velocity field has been proposed by Kolmogorov and Oboukhov ^22),(35.It is believed that the origin of intermittency may come from the coupling between inertial and dissipate scales in spectral k-space, which is the usual reciprocal (Fourier) space ^{20),(21),(22),(35),(40}, this can be shown by using a refined self similarity approach ³⁴, but our comprehension remains still elusive. Some other models have been recently proposed such as a phenomenological theory relying on the so-called singularity spectrum in both the Eulerian (spatial) and the related Lagrangian (temporal) description of the fluid velocity ²³. In 1985, Frisch and Parisi proposed to explain such scaling function's behavior in a heuristic way, in order to link the fast fluctuations of the flow velocity field regularity to the Hölder exponents variations ⁴⁰.

Multi-fractal analysis or approach (MFA) is a well-suited way to study and quantify those local variations ^{1),(4),(6),(7),(8),(10),(11),(19),(25),(26),(42}. Historically, it was introduced first in mathematical and theoretical physics to understand local behaviour and invariant scaling properties of functions, measures, and stochastic process trajectories ^{4),(6),(18),(32),(39),(43}. Before MFA, it was admitted that fractality was the possible signature of an underlying well-organised structure.But some mathematical researches have invalidated this approach and showed that natural and experimental signals are in general multi-fractal, fractality is thus just a special case of multi-fractal behavior ^2),(6),(26.

This has opened a new branch of applied and computational mathematics in order to study phenomena which exhibit spatial and/or time dynamical structures such as in physics and chemistry, geophysics, astrophysics, telecommunications, meteorology, biology, economics and finance for instance. A good review is given in ^1),(6.

We aim in this article to show how (min,+)-waveletsis an easy algorithm to implement in order to perform MFA. Some well-known definitions about Hölder exponents and fractals arepresented in Section 2. One presents briefly at the end of this section the so-called Wavelet-transform modulus-maxima method (WTMM) ^1),(6. We remind in Section 3 the main results of (min,+)-analysis and introduce the (min,+)-wavelets. One applies them numerically inSection 4 to the Riemann serie, and to the Mandelbrot binomial cascade. The interest of thismeasure is that it is a versatile mathematical toy-model used in hydrodynamic turbulence, geophysics and finance for instance ⁶. Section 5 is devoted to numerical comparison of both (min,+)-waveletsand WTMM methods to the calculations of scaling functions and singularities spectra of Mandebrot cascades according to theoretical results.

2 FRACTALS

2.1 Self-similar sets and Hausdorff dimension

According to B. Mandelbrot ²⁶, a fractal is an object a part of which is in some way similar to the whole. Fractal objects are present everywhere in Nature. The fractal behavior is common to hydrodynamic turbulence ²⁶⁾⁽³⁷, the Feynman paths in quantum mechanics ⁹, financial time series ³⁶, terrestrial landscape and thin film surfaces ^3),(5, etc. The most remarkable mathematical examples of fractal sets are: triadic Cantor set, Sierpinski gasket, Koch triadic curve etc (see e.g. ¹² for more detailed account).

In contrast to classical geometrical objects, the dimension of a fractal set is not an integer number. For a classical object, if covered with balls (or boxes) of size δ, the total number of balls required for the minimal covering increases as

(2.1)

For regular geometrical objects the dimension D is always integer: D = 1 for line, D = 2 for surface, etc. In general case D may, or may not be an integer. It is then convenient to characterize fractal sets by the power behavior of corresponding measures. Let us consider a set 𝒜 and a function M(d) = Σ_i δ^d , which is a measure defined on the coverage of the set 𝒜 by δ-balls, δ → 0. If there exists such d ∊ ℝ, that the measure M_d (𝒜) has a discontinuity at d = D_F

(2.2)

the set 𝒜 is said to have Hausdorff (or fractal) dimension D_H .

For example, the fractal dimension of the 1/3-Cantor set is easily derived from its construction procedure. In the i-th generation as shown in Figure 1, we have N = 2ⁱ equal parts of length l = 3^-i . Thus, one gets N = 2ⁱ = D^H = D^F is less than 1, which is the dimension of a differentiable curve^6),(39. =exp(-ln 2/ln 3) ⇒ ≈ 0.6309.

Figure 1:
The construction of the triadic Cantor set from the unit length rode.

2.2 Multifractals

The theory of multi-fractals (fractal objects), with the dimensions of subsets dependent on the singularity strengths - stems from the Mandelbrot papers and was developed by several authors ^10),(37.

2.2.1 Hölder exponents and multi-fractal spectrum

There are two types of fractals: regular (or geometric) fractals, as those mentioned above, and random fractals⁴¹, i.e. self-similar objects without any regular geometrical structure, e.g. the path of Brownian particle. Both of them are characterized by singularity strength (or Lipschitz-Hölder exponent) and the fractal (Hausdorff) dimensions D(α) of all subsets I_α with the singularity strength equal to α. Some functions can exhibit different properties of regularity at each point. Usually some notions such as continuity and derivability at a point are used to quantifythe regularity of a function. Hölder exponent is a well-suited quantity which permits to merge and link such pointwise properties. Let's remind first some definitions.

Definition 1. Let x ∊ ℝ^m , f ∊ L ^∞ _loc(ℝ^m , ℝⁿ )^. f ∊ C^α (x) if and only if it exists a constant C > 0 and α ∊ [0, 1], such as for y sufficiently close to x, ||f(y) - f(x)|| ≤ C||y - x||^α .

Definition 2. Hölder exponent h_f of a function f at point x ∊ ℝ^m is defined as h_f (x) = sup{α ≥ 0 : f ∊ C^α (x)}

Definition 3. The iso-Hölder exponents of h-order singularities for a function f is defined as S_f (h) = {x : h_f (x) = h}.

Remark 1. Since some interesting phenomena exhibit sets S_f (h) which are often fractal, dense or random, therefore the Lebesgue measure and the Minskowski dimension are not well-suited to distinguish different S_f (h) ⁶. Thus, the relevant dimension which has to be used is the Hausdorff dimension dim_H .

Definition 4. The multi-fracal (or singularities) spectrum D_f of a function f is defined as the real positive number D_f (h) = dim_H S_f (h).

Definition 5. If D_f is constant according to h, the signal will be called mono-fractal.

Any subset of a regular geometric fractal (mono-fractal), is similar to the whole fractal, and hence has the same fractal dimension. Therefore, for simple geometrical fractals such as for example Cantor set, or more sophisticated functions such as the Weierstrass and Weierstrass-Mandelbrot functions ³², there is no dependence between the singularity strength of the subsets and their fractal dimensions. In contrast, different subsets of real fractals present in Nature may havedifferent dimensions according to h. Thus, for real fractals appearing in Nature, such dependence is often present, sometimes having intrinsic behavior.

2.2.2 Heuristic approach of multi-fractal analysis

The most educational and simple example to figure out what multi-fractal sets are, is the heuristic approach of Frisch and Parisi in hydrodynamic turbulence. They postulated that for a particular h and for each point x ∊ S_f (h), the small fluctuations of the flow velocity field v between the two points x and x + l behave like

||x(x + 1) - v(x)|| ∼ ||I||^h

If D _v(h) > 0, one can state from (1.1) and with geometrical arguments that

For ||I|| → 0, the main contribution to this integral is obtained for

which shows that ξ_v is the Legendre transform of D _v, and explains therefore its concavity. Its inverse Legendre transform has the same property of concavity since

(2.3)

This heuristic approach can be generalized for functions f : ℝ^m → ℝ:

(2.4)

2.2.3 Thermodynamic formalism

The MFA has been established and developed to account separately for the subsets of different singularity strength and to reveal the scaling properties of singular measures arising in different physical situations ^17),(27, first of all in hydrodynamic turbulence. It accounts for the statistical scaling properties of singular measures by means of singularity spectrum, which determines the behavior of D(h) just like the poles of a complex variable function define its behavior ¹³.

If a fractal subset

B_x0 = {x|ρ(x, x₀) ≤ l}

of the set 𝒜, where ρ is a metric on A and l is the diameter of B, is covered by δ-balls centered at x_i , then the measure of 𝒜 is

(2.5)

where δ _{x i} is a ball centered at x_i . For a mono-fractal set B the power behavior of μ(B) in δ → 0 limit is described by the singularity strength of the measure

where α does not depend on x₀. In general multi-fractal case the power behavior of the measure can be dependent on the point. One defines D(h) as the fractal dimension of the set of all points x_i ∊ A, such that μ(B _{x i} ) ∼δ^α , where B _{x i} is a sufficiently small neighborhood of x_i . The simplest measure (2.2) is incapable to account for the variety of all multi-fractal properties. In MFA ^{1),(10),(13),(29} the properties of singular objects are described in terms of the weighted measure M_d (q, δ), more general than M_d (δ):

(2.6)

The practical reason for introducing a weighted measure (2.6) is clear enough ⁶. If one considers a set 𝒜 covered with the cells of size δ, it may happen that some cells contain only a few points of 𝒜, while some other cells contain plenty of them. The Hausdorff measure (2.2) accounts for all non empty cells with the same weight. This is unfair either to low populated cells or to densely populated cells. What one needs is a method separately sensitive to both extreme cases. This method, called weighted curdling, is based on the measure (2.6), with μ_i = N_i/N being the relative population of the i-th δ-cell, where N = #𝒜. In the case of negative q the measure is more sensible to low populated cells, the positive q measures are more sensitive to densely populated cells ⁶.

The multi-fractal formalism associates the fractal dimension D(h) to the fractal subset of a given singularity strength h of the considered set. By thermodynamic analogy it is possible to consider

(2.7)

as a partition function, with q regarded as a counterpart of the inverse temperature.

The power behavior of the partition function (2.7) in δ → 0 limit is expressed in terms of the mass exponent ξ(q), an analog of free energy in thermodynamics. The scaling exponent ξ(q) and the fractal dimension D(h) are related then by means of the Legendre transform:

2.3 Wavelet-transform modulus-maxima method (WTMM)

As it was shown in ^28),(30, the partition function Z(q, a) can be directly evaluated using the calculated set of linear wavelet coefficients W_ψ (α, b):

(2.8)

In this construction, to calculate the partition function for a given scale α ₀ one has to sum up over all maxima lines l: (b, α ≤ α ₀) starting from (b, α ₀) and going to smaller scales α < α₀ . In practice, this often means that it is sufficient to take a section W_ψ (α = α ₀ ,b) and sum up over all maxima in b. The wavelet coefficients in the partition function (2.8) are taken in accordance to ^28),(30 in L ¹ norm W_ψ (α, b)[f] = f(x)dx and are based on usual linear wavelets basis set such as gaussian derivatives wavelets for instance ^6),(1. It is named Wavelet-Transform Modulus-Maxima method (WTMM) ^6),(1.

3 (min, +)-WAVELETS ANALYSIS

We aim to present in this paper an alternative scheme which uses (min, +)-wavelets ratherthan linear wavelets.

According to equations (2.3) and (2.4), (min, +) transform, which has been already defined within (min, +) analysis^{15),(16),(31),(32} is an interesting potential candidate to perform multi-fractal analysis. One tries in this article to test it on well-known multi-fractals signals such as Mandelbrot cascades and Riemann's one.

This one consists to replace in the scalar product definition of two real-valued functions f and g defined on a domain X, the real number field (ℝ, +, ×)with the (min, +) dioid (ℝ ⋃ {+∞},min, +). The classical scalar product 〈f, g〉 = ∫ _{x ∊ X} f(x) g(x) dx becomes then the(min, +) scalar product ^15),(32:

In (min, +) analysis, a set of non-linear transforms has been introduced for lower semi-continuous functions ^15),(31, the so-called (min, +)-wavelets transforms which are definedfor a function f: ℝⁿ → α ∊ ℝ⁺ and b ∊ ℝⁿ such as: and for all

(3.1)

where ĥ is a basis analysing function (upper semi-continuous and inf-compact) verifying ĥ(0) =, like the following functions:

Since T ^- _f (a, x) ≤ f(x) for all a > 0, T ^- _f (a, x) is a lower hull of f(x). For any lower bounded and lower semi-continuous function, one has a reconstruction formula like in the linear wavelets theory ⁶:

(3.2)

which can be simplified within the (min, +) theory in

(3.3)

The (min, +)-wavelets analysis will be based on simultaneous analysis of lower hulls T ^- _f (a, b), and upper hulls of f represented by T ⁺ _f (a, b) defined by:

(3.4)

For the upper hulls T ⁺ _f (a, b), we have a reconstruction formula which is symmetric to lower hulls T ^- _f (a, b) (3.2, 3.1):

(3.5)

which simplifies as well as:

(3.6)

Definition 6. - (min, +)-wavelet is defined as the couple {T ^- _f (a, x), T ⁺ _f (a, x)} ∀a ∊ ℝ⁺ , the a-oscillation of f is defined as:

(3.7)

T^-_f (a, x) (respectively T ⁺ _f (a, x)) are functions decreasing with scales (respectively increasing) and converging to f _*(x) (respectively f ^*(x)), the lower semi-continuous closure of f (respectively upper semi-continuous closure) when the scale tends to 0 ^{15),(16),(31),(32}. An example of (min, +)-wavelets decomposition is shown on Figure 2. The following theorem guarantees that the (min, +)-wavelets decomposition is well-defined.

Figure 2:
(min, +)-waveletsdecomposition for the Weierstrass function W(t)= ĥ ₂ for scales k·10^-1 with k from 1 to 10. 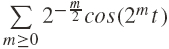with the analysing function

Theorem 1. For each analysing function ĥ, one has¹⁶:

T^-_f (a, x) ≤ f _*(x) ≤ f(x) ≤ f ^*(x) ≤ T ⁺ _f (a, x).

Remark 2. In the case of analysing function ĥ _∞, one has T ⁺ _f (a, x) = sup_{|x - y| ≤ a} f(y), T ^- _f (a, x) = inf_{|x - y| ≤ a} f(y) and ∆T_f (a, x) = sup|_{x - y| ≤ a} f(y) - inf_{|x - z| ≤ a} f(z) corresponds to the a-oscillation defined in one dimension by Tricot ³⁹:

We remind another important result linking local oscillations to Hölder exponents which is stated in the following theorem ³²:

Theorem 2. The function f is Hölderian at point x₀ , with exponent H, 0 < H ≤ 1, if and only if it exists a constant C such as for all a, one has one of the following conditions:

(3.8)

(3.9)

Remark 3. Since H when a → ∞, inequation (3.9) can be considered as a generalisation of (3.8). →

4 CALCULATIONS OF MULTI-FRACTAL SPECTRUM

Hölder exponent gives an incomplete information about the singularities' nature at a point. One needs then another analysing tool to quantify and classify them. The Hölder exponent calculations can be numerically unstable since it can be everywhere discontinuous. Thus, the computation of singularities spectrum is not possible directly from its definition, and one has to get it from other quantities. The (min, +)-wavelets permits to generalise results established for mono-fractal functions ^1),(6 to multi-fractal ones and to compute directly the scaling function ξ_f for f defined on a domain 𝒯 ⊂ ℝ^m:

(4.1)

The scaling function value for each p ∊ ℝ can be viewed as the slope of linear part of the curve at small scales representing the logarithm of oscillations p-order moment ∫_𝒯[ΔT_f (s, t)]^p dt according to the logarithm of scales s.

Thus, within the (min, +)-analysis framework and because of theorem (2), one can define α-Legendre transforms which yields to another definition of the scaling function and the singularities spectrum:

(4.2)

and

(4.3)

Remark 4. When α → ∞, one recovers the usual Legendre transforms (2.4). Numerical calculations are more stable with α ≫ 1. Therefore, we will only use h_∞ as analysing function in the numerical calculations.

The basic flowchart is very simple

1. Compute ∆T_f (s, t) with (min, +)-wavelets for scales s ∊ S ⊂ ℝ^+* and for t ∊ 𝒯 ⊂ ℝ^m.

2. Perform linear regression at small scales s (s → 0⁺) with mean of relation (4.1) and classical integration methods in order to obtain ξ_{f ,(min, +)} (p)³².

3. Minimisation of equation (4.3) in order to get singularities spectrum D_{f ,(min, +)}.

We exhibit below the numerical applications of this flowchart to Riemann serie and Mandelbrot binomial measure.

4.1 Riemann serie

Riemann proposed in 1854 in his research thesis the definition of his famous integral. Cauchy had already established that the integral of a piecewise continuous function is well-defined. In order to show that his integral generalises the Cauchy's one, Riemann applied it to the so-called Riemann serie

where x ↦ [x] is the ceiling function which gives the smallest integer not less than x. One can immediately prove that it is Riemann-integrable but has dense discontinuities set, which means that it is not Cauchy-integrable. It is one of the first example of multi-fractal function and it has been proved that its singularities spectrum is D(h) = h for h ∊ [0,1], and scaling function is

The previous flowchart is applied to Riemann serie with 2¹⁰ points in Figure 3. Numerical results are exhibited on Figures 4 and 5 and proves that MFA of Riemann function with (min, +)-wavelets decomposition is well-suited and efficient to find the right spectrum and scalingfunction for the Riemann serie.

Figure 3:
Representation of the Riemann serie R(x) = ¹⁰ points. with 2

Figure 4:
Exact and numerical scaling functions of the Riemann serie R(x) = ĥ _∞ analysing function. Relative error in l ²-norm is about ≃ 2.50%. 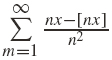with

Figure 5:
Exact and numerical singularities spectra of the Riemann serie R(x) = ĥ _∞ analysing function. Relative error in l ²-norm is about ≃ 4.92%. 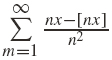with

4.2 Mandelbrot binomial measure

The multi-fractal formalism was first successfully applied in physics to the description of cascade processes in hydrodynamic turbulence, Richardson's one for example ^33),(20. It is often named binomial multiplicative process or Mandelbrot cascade and is the simplest example of a multi-fractal set. This model describes a non-equal sharing of the energy flux from a large eddy of size l to 2^d small ones of size l/2, where d is space dimension. Let us give an example in one dimension by considering a population of arbitrary objects, initially distributed homogeneously on a unit interval [0,1] and a process, which redistributes the population with the probability p to the left half of the interval, and with probability q = 1 - p to the right half. After the first iteration we will have the probability measure (p, q) for the whole interval, after the second iteration (p ², pq, qp, q ²), etc. An example of such cascade is shown on Figure 6 with p=0.25. It is easy to write the exact multi-fractal spectrum of this process as ⁶:

(4.4)

which is obviously concave since it is the opposite of a convex combination.

Figure 6:
Mandelbrot cascade in one dimension for probability p = 0.25 and 10 levels.

Figures 7 and 8 show clearly that the multi-fractal approach with (min, +)-wavelets finds the right scaling function and singularities spectrum of the Mandelbrot cascade of Figure 6.

Figure 7:
Mandelbrot cascade exact and numerical scaling function for probability p = 0.25 and 10 levels with ĥ _∞ analysing function. Relative error in l ²-norm is about ≃ 2.50%.

Figure 8:
Mandelbrot cascade exact and numerical spectra for probability p = 0.25 and 10 levels with ĥ _∞ analysing function. Relative error in l ²-norm is about ≃ 5.62%.

5 COMPARISON BETWEEN (min, +)-WAVELETS AND WTMM METHODS ON MANDELBROT CASCADE

One would like to illustrate efficiency of (min, +)-wavelets approach compared to WTMM one. Thus, we applied to the Mandelbrot cascade the WTMM method with mean of gaussian wavelet of level 7, which is defined as the function

Results are exhibited in Figures 9 and 10. The errors are respectively for the scaling function and the singularities spectrum about 11.65% and 37.68%. This has to be compared to the (min, +)-wavelets method ones which are respectively about 2.50% and 5.62% as shown in the previous section. Those results prove clearly that for the Mandelbrot cascade, (min, +)-wavelets method is clearly much more accurate than WTMM one, which uses linear wavelets decompositions, which depend of basis set used, and of the way integrals are computed to get decomposition coefficients. Such usual methods are in the best cases N log² ₂(N) where N is the number of real space points used in discretization ^38),(6. With (min, +)-wavelets decomposition, computational time scales linearly like O(N), since it only uses minimization of a set of values. Moreover, (min, +)-wavelets method can deal with larger set of functions.

Figure 9:
Mandelbrot cascade exact and numerical scaling function for probability p = 0.25 and 10 levels computed with WTMM method using continuous gaussian wavelet of level 7 as analysing function. Relative error in l ²-norm is about ≃ 11.65%.

Figure 10:
Mandelbrot cascade exact and numerical spectra for probability p = 0.25 and 10 levels computed with WTMM method using continuous gaussian wavelet of level 7 as analysing function. Relative error in l ²-norm is about ≃ 37.68%.

6 CONCLUSION

During several decades many modellings of phenomena in natural sciences such as physics, chemistry, biology, and in other fields such as finance, economics, etc, have been based on the well-known brownian motion. This approach permitted to embed their underlying structure within the fractal theory. But new experiments and mathematical analysis have shown that fractal theory was not sufficient and able to describe signals which exhibit the same irregularitieseverywhere in the same way, and could be classified according to certain mathematical quantities. Nowadays, MFA with mean of wavelet theory seems to be a good candidate to perform such kind of accurate analysis. We have proposed in this paper to use the (min, +)-wavelets for Riemann serie and Mandelbrot cascade, which are known to be multi-fractal. The comparisons between numerical calculations with both (min,+)-wavelets and WTMM approaches, and theoretical ones for scaling functions and singularities spectra of those classical examples and especially for MandelBrot cascade, which is the toy model for hydrodynamic turbulence and other phenomena, have shown that multi-resolution analysis with mean of (min,+)-wavelets is relatively efficient and accurate, easy to implement method and that it can be interesting to test it eventually to other kinds of data.

7 ACKNOWLEDGEMENTS

We thank Mikhail Altaisky, Janos Polonyi, René Voltz for useful and helpful discussions about turbulence and wavelets.

REFERENCES

• ¹
  A. Arneodo, F. Argoul, E. Bacry, J. Elezgaray & J.-F. Muzy. Ondelettes, multifractales et turbulence. Diderot, Paris, (1995).
• ²
  H.D.I. Abarbanel, R. Brown, J.J. Sidorowich & L.Sh. Tsmiring. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys., 65(4) (1993), 1331-1392.
• ³
  M.V. Altaisky, L.P. Chernenko, V.M. Balebanov, N.S. Erokhin & S.S. Moiseev. Multifractal analysis of AFM images of Nb thin film surfaces. Particles and Nuclei Letters, 2(99) (2000), 14-26.
• ⁴
  A. Arneodo, G. Grasseau & M. Holschneider. Wavelet transform of multifractals. Phys. Rev. Lett., (1988), 2281-2284.
• ⁵
  M.V. Altaisky, V.V. Ivanov, S.A. Korenev, O.L. Orelovich, I.V. Puzynin & V.V. Chernik. Fractal structure formation on the surfaces of solids subjected to high intensity electron and ion treatment. JINR Rapid Communications, 82 (1997), 37-46.
• ⁶
  M. V. Altaisky. Wavelets, Theory, Applications and Implementation. Universities Press, (2005).
• ⁷
  A. Aldroubi & M. Unser. Families of multiresolution and wavelet spaces with optimal properties. Num. Func. Anal. Optim., 14 (1993), 417-446.
• ⁸
  A. Aldroubi & M. Unser. Wavelets in biology and medicine. CRC Press, (1999).
• ⁹
  L.F. Abbott & M.B. Wise. Dimension of quantum-mechanical path. Am. J. Phys., 49 (1981), 37-39.
• ¹⁰
  R. Benzi, G. Paladin, G. Parizi & A. Vulpiani. On multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A, 17 (1984), 3521-3531.
• ¹¹
  S. Dahlke, W. Dahmen & I. Weinreich. Multiresolution analysis and wavelets on s² and s³ Numer. Funct. Anal. and Optimiz., 16 (1995), 19-41.
• ¹²
  J. Feder. Fractals. Plenum Press, (1988).
• ¹³
  U. Frish, M. Nelkin & P. L. Sulem. A simple dynamical model of intermittent fully developed turbulence. J. Fluid. Mech., 87 (1978), 719-736.
• ¹⁴
  Y. Gagne. Etudes expérimentales de l'intermittence et des singularités dans le plan complexe et turbulence développée. Thèse de l'Université de Grenoble, (1987).
• ¹⁵
  M. Gondran. Analyse minplus. C. R. Acad. Sci. Paris, 323(323) (1996), 371-375.
• ¹⁶
  M. Gondran. Convergences de fonctions à valeurs dans R^k et analyse minplus complexe. C. R. Acad. Sci. Paris, 329 (1999), 783-788.
• ¹⁷
  T.C. Halsey, M.H. Jensen, L.P. Kadanoff, I. Procaccia & B.I. Shraiman. Fractal measures and their singularities: the characterization of strange sets. Phys. Rev. A., 33(2) (1986), 1141-1151.
• ¹⁸
  B.R. Hunt. The hausdorff dimension of graphs of weierstrass functions. Proceedings of the American Mathematical Society, 126 (1998), 791-800.
• ¹⁹
  L.P. Kadanoff. Scaling and Multiscaling: Fractals and Multifractals. Number 29. Chinese Journal of Physics, (1991).
• ²⁰
  A. Kenoufi. PhD Thesis: "Density functional Theory and Renormalisation Group". University of Strasbourg, (2004).
• ²¹
  A.N. Kolmogorov. The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Number 30. Dokl. Akad. Nauk, SSSR, (1941).
• ²²
  A.N. Kolmogorov. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. Number 13. JFM, (1962).
• ²³
  L. Chevillard, B. Castaing, A. Arneodo, E. Lévêque, J.-F. Pinton & S.G. Roux. A phenomenological theory of Eulerian and Lagrangian velocity fluctuations in turbulent flows. Comptes Rendus Physique, 13(9) (2012), 899-928.
• ²⁴
  P.C. Martin & L.P. Kadanoff. Hydrodynamic Equations and Correlation Functions. Number 24. Ann. Phys., (1963).
• ²⁵
  S. Mallat. A theory for multiresolution signal decomposition: wavelet transform. Preprint GRASP Lab. Dept. of Computer an Information Science, Univ. of Pensilvania, (1986).
• ²⁶
  B. Mandelbrot. The fractal geometry of Nature. Freeman, San Francisco, (1982).
• ²⁷
  B. Mandelbrot. Fractals and Multifractals: Noise, Turbulence and non-fractal Patterns in Physics. Nijhof, Dordrecht, (1986).
• ²⁸
  J.F. Muzy, E. Bacry & A. Arneodo. Wavelets and multifractal formalism for singular signals: Application to turbulence data. Phys. Rev. Lett., 67 (1991), 3515-3518.
• ²⁹
  J.F. Muzy, E. Bacry & A. Arneodo. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. Phys. Rev. E, 47 (1993), 875-884.
• ³⁰
  J.F. Muzy, E. Bacry & A. Arneodo. Singularity spectrum of fractal signals: Exact results. J. Stat. Phys., 70(3/4) (1993), 635-674.
• ³¹
  M. Minoux & M. Gondran. Graphs, Dioids and Semirings. Springer, (2008).
• ³²
  A. Kenoufi & M. Gondran. Numerical calculations of Holder exponents for the Weierstrass functions with (min,+)-wavelets. Number 3. Tend. Mat. Apl. Comput., 15 (2014).
• ³³
  C. Meneveau & K.R. Sreenivasan. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett., 59 (1987), 1424-1427.
• ³⁴
  N.T. Ouelette, R. Friedrich, M. Wilczek, H. Xu & E. Bodenschatz. Generation of Lagrangian intermittency in turbulence by a self similar mechanism. Number 15. New Journal of Physics, (2013).
• ³⁵
  A.M. Oboukhov. Some specific features of atmospheric turbulence. Number 13. JFM, (1962).
• ³⁶
  E.E. Peters. Chaos and order in Capital Markets. John Wiley & Sons Inc., (1991).
• ³⁷
  G. Parisi & U. Frish. On the singularity structure of fully developed turbulence. In M. Chil, R. Benzi, and G. Parisi, editors, Turbulence and predictability in geophysical fluid dynamics, Proc. Int. School of Physics 'E.Fermi', pages 84-87, Varenna, Italy, 1985. North-Holland, Amsterdam.
• ³⁸
  B. Torrésani. Analyse continue par ondelettes. Interéditions/Editions du CNRS, (1995).
• ³⁹
  C. Tricot. Courbes et dimension fractale. Springer-Verlag, (1993).
• ⁴⁰
  G. Parisi & U. Frisch. Fully developed turbulence and intermittency. Proc. Internat. Summer School Phys. Enrico Fermi, pages 84-88, (1985).
• ⁴¹
  R.F. Voss. Random fractals: characterization and measurement. In Scaling Phenomena in Disordered Systems, volume 133 of NATO Advanced Study Institute series B. Plenum Press, New York, (1985).
• ⁴²
  O.V. Vasilyev, S. Paolucci & M. Sen. A multilevel wavelet collocation method for solving partial differential equations in a finite domain. J. Comp. Phys., 120 (1995), 33-47.
• ⁴³
  K. Weierstrass. Uber continuirliche funktionen eines reellen arguments, die für keinen werth des letzteren einen bestimmten differentialquotienten besitzen. Karl Weiertrass Mathematische Werke, Abhandlungen II, Gelesen in der Königl. Akademie der Wissenchaften am 18 Juli 1872, (1967).

Publication Dates

• Publication in this collection
  May-Aug 2016

History

• Received
  29 Sept 2014
• Accepted
  09 Aug 2016