text new page (beta)
English (pdf)
Article in xml format
Automatic translation
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
INTRODUCTION
In geology, the understanding of structures can be too complex to be reached using only field methods. Remote sensing topographic survey techniques such as LiDAR (Light Detection And Ranging, also called laser scanning), and photogrammetry are able to provide greater amount of information, as their resulting digital models allow (Bistacchi et al. 2015, Hodgetts 2013):
Detailed quantitative description of geological features regarding geometry and spatial relationships;
Collection of large amounts of data, evenly distributed along an area or outcrop, providing a statistical basis for modeling;
Unified analysis of large-scale outcrops, even at reservoir scale;
True and reliable documentation that can be used for multiple purpose;
Three-dimensional (3D) outcrop navigation/exploration, providing “access”to out-of-reach or hazardous areas.
Among such techniques, SfM-MVS (Structure from Motion - Multi-View Stereo) workflow has gained strength in the geosciences over the past years (Tab. 1), mostly because when compared to other digital surveying it is capable of producing high-resolution data at low cost, fast and virtually independent of spatial scale. The final result of SfM-MVS is a detailed 3D model - also referred by some authors as Digital Outcrop Model (DOM) (Pringle et al. 1999, Zahm et al. 2016, Silva et al. 2014), or virtual outcrop (Pringle et al. 2001, Tavani et al. 2014) -, that can be used as a point cloud or as a triangular mesh. As shown in Table 1, most applications of SfM-MVS are dedicated to extraction of geometrical properties of discontinuities, mostly faults and fractures, which are simple structures. An example of a complex structure that can take advantage of the use of SfM-MVS are clastic dikes, which are discordant subvertical sheets, tabular bodies of clastic sediments that can form by hydraulic fracturing and infilling (Hargitai & Levi 2014). Even for traditional field survey, the analysis of such structures can be challenging and, to date, no work has presented it through the use of 3D models. Thus, the objectives of this paper are twofold:
use SfM-MVS to generate a DOM of an outcrop of the Corumbataí Formation (Permian, Paraná Basin), which contains a remarkable exposition of clastic dikes;
extract geological attitudes of clastic dikes from the DOM and compare them with field-collected data in order to discuss the pros and cons of using digitally-derived data in structural analysis.
Table 1. Examples of Structure from Motion - Multi-View Stereo (SfM-MVS) applications in the geosciences.
| Subject | Application | References |
|---|---|---|
| Structural geology and geotechnics | Structural mapping | Gates & Haneberg (2012) |
| Extraction of the orientations of the discontinuities | Deb et al. (2008), Sturzenegger & Stead (2009), Assali et al. (2014), Vasuki et al. (2014), Buyer & Schubert (2016), Viana et al. (2016), Riquelme et al. (2017) | |
| Surveys of trenches, rock exposures and hand specimens for paleo-seismology and structural geology | Bemis et al. (2014) | |
| Fault analysis | Tavani et al. (2016) | |
| Geo-mechanical classification | Riquelme et al. (2016) | |
| Kinematic analysis of rock slopes | Jorda-Bordehore et al. (2017) | |
| Accuracy of SfM and LiDAR for structural measurements | Cawood et al. (2017) | |
| Orientation measurements of complex folds | Zachariah & Terry (2018) | |
| Topography and bathymetry | Extracting shallow stream bathymetry | Dietrich (2017) |
| Topography with UAVs | James & Robson (2014), James et al. (2017) | |
| Generation of high-resolution DEM | James & Robson (2012), Carbonneau & Dietrich (2017), Mali & Kuiry (2018) | |
| General geology | Building a virtual outcrop (3D geology) | Tavani et al. (2014), Zahm et al. (2016) |
| UAVs for mapping dolomite geobodies | Madjid et al. (2018) | |
| Reservoir analysis | Geomechanical and fluid flow models | Bisdom et al. (2017) |
| Characterization of reservoir analogs | Biber et al. (2018) |
LiDAR: light detection and ranging; UAVs: Unmanned Aerial Vehicles; DEM: Digital Elevation Models; 3D: three-dimensional.
Considering that the use of SfM-MVS in the geosciences is expanding rapidly, and that a successful DOM generation might involve more factors than initially considered by the non-experienced user, we also present a brief summary of the processes and algorithms involved in the SfM-MVS workflow, as well a list of best practices for fieldwork, derived from the experience gained by the authors in the development of this project.
STUDY AREA AND GEOLOGICAL SETTING
This study focused on a NE-SW (facing NW) roadside rocky outcrop near Limeira city, state of São Paulo, Brazil, km 161.5 of SP-348 Bandeirantes highway (Fig. 1). The outcrop is a ∼500 m-long and ∼30 m-high exposition of the Corumbataí Formation (Permian, Paraná Basin), composed of siltstone intercalated with fine sandstone and carbonate layers, intruded by a swarm of clastic dikes (Riccomini et al. 1992, Perinotto et al. 2008, Turra 2009).
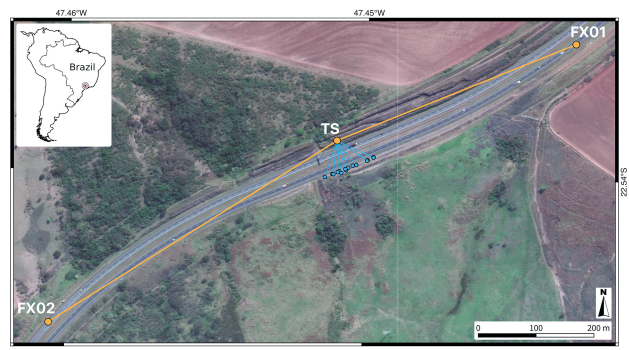
Figure 1. Study area location in Brazil (inset). Positioning of the total station (TS), fixed points (FX01 and FX02) and targets distributed on the outcrop surface (blue points).
Syn-depositional and postdepositional dikes are distinguished depending on time of fracture infilling (Allen 1982), and two subtypes can be categorized based on the formative process: injection clastic dikes and sedimentary (or depositional) dikes. The first type are liquefaction structures that form as water-saturated granular material experiences an increase in pore fluid pressure, typically occurring in cohesionless or nearly-cohesionless sediments and may be caused by cycles of sheer stresses during strong earthquake events (M > 6.5 - Hargitai & Levi 2014).
In the studied outcrop, clastic dikes are vertical to near-vertical tabular to ptygmatic-folded bodies of massive fine sandstone cutting through pelitic layers (Fig. 2). The dikes occur in four sedimentary levels, being more numerous on the lower level. The top of this level is marked by a well-defined surface with structures interpreted as sand extrusions. Despite the scattering of data, Turra (2009) described a general NNW orientation trend of clastic dikes and a N-NE trend of sand extrusions’ feeder dikes (Fig. 3A).
Figure 2. Perspective view of generated Digital Outcrop Model (DOM). See Supplemental Material for camera positions and ground control points (GCPs) (Suppl. Fig. S5).
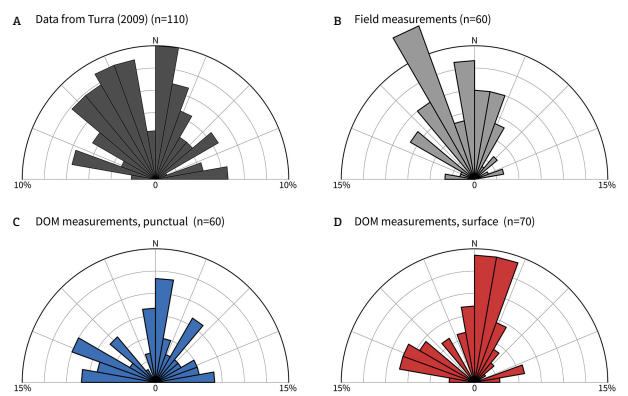
Figure 3. Rose diagrams: (A) measurements from Turra (2009); (B) all field measurements; (C) Digital Outcrop Model (DOM) measurements (punctual); (D) DOM measurements (surface). All diagrams have 10º petals.
Riccomini et al. (1992) were the first authors to associate the formation of clastic dikes in the Corumbataí Formation to a seismic event. Later, Riccomini (1995) identified two sets of dikes orthogonal to each other with predominance in the NE-SW direction, interpreted as the direction of the maximum horizontal tension vector and associated with the early stages of the Pangea rupture. Chamani et al. (1992), Fernandes & Coimbra (1993) and Riccomini et al. (1996) also interpreted some features in the Permotriassic units of the Paraná Basin as seismites.
Perinotto et al. (2008), analyzing three different sites, concluded that due to the scatter of measurements the dikes occupied pre-existing fractures or those generated by hydrofracturing under local stress, being unrelated to regional tectonic patterns as suggested previously, although to Chamani (2015) the lack of a careful statistical analysis (presenting orientation data only as great circles in a stereonet, for example) by Perinotto et al. (2008) hinders an objective assessment of their conclusions. The discussion brought by these works point to the uncertainty in interpreting clastic dikes and their associated structural markers, which justifies the experimentation of structural analysis based on SfM-MVS models as a more objective mean for assessing/ascertaining orientation data. Recent studies (Tohver et al. 2013, 2018) related the seismicity that generated the dikes to the impact event that formed the Araguainha structure, at the Permian-Triassic boundary.
STRUCTURE FROM MOTION MULTI-VIEW STEREO
In the geosciences, the development of remote digital surveying methods allowed not only the increase in collection speed and data density, but also enabled the surveying in physically inaccessible places. Among such techniques, there are traditional photogrammetry, laser scanning and SfM-MVS.
Structure from Motion (SfM) is a recent tool that has had an impact on the field of geosciences in recent years. It enables the generation of high-precision 3D models from two-dimensional (2D) images in a simple way, bringing the power of digital models to non-experts. An important advantage of this method, compared with the traditional photogrammetric workflow, is that each feature is defined from a redundant number of photos (Snavely et al. 2006), and error estimates are just another output from model inversion. This ensures the high quality of the results, because points with precision lower than a given threshold are automatically rejected by the inversion algorithm (Bistacchi et al. 2015).
As put by Carrivick et al. (2016), most authors in geosciences cite in a simplified way the SfM algorithm as the sole responsible for creating the 3D model. When we look at the processing of the set of images, in brief, it goes through three main steps:
the recognition of points in common between the images of the set and the calculation of the x, y, z position of each point;
construction of a sparse point cloud (also referred as coarse cloud);
the refinement of the model and generation of a dense point cloud.
SfM algorithms are responsible only for the first two steps of the process. The third step is performed by the Multi-View Stereo (MVS) methods and, therefore, the most correct would be to refer to the SfM-MVS method.
In this section, we would like to give a brief summary of the processes and algorithms involved in SfM-MVS workflow to generate a Digital Outcrop Model (DOM) (Fig. 4). Most of the information provided here is from the work of Carrivick et al. (2016) and the reader is referred to it for further detailing.
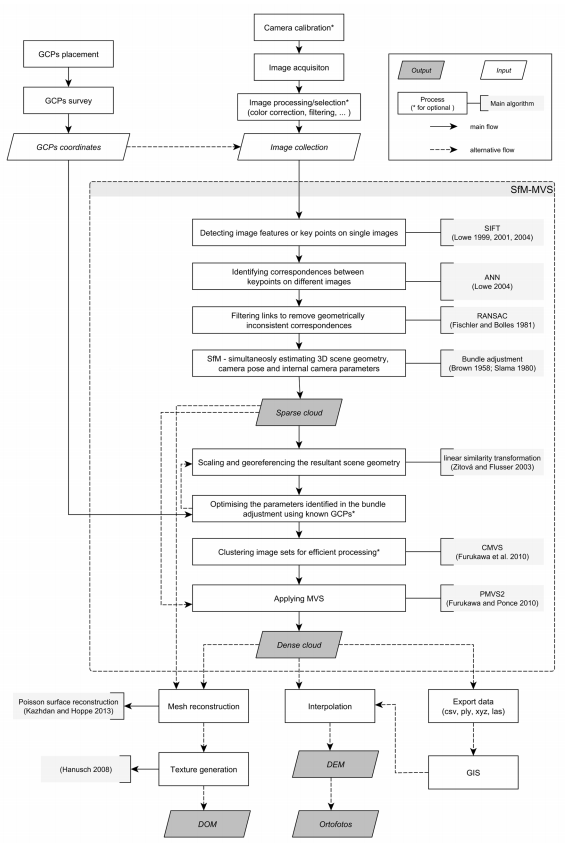
Figure 4. Simplified flowchart showing the main steps involved on a Digital Outcrop Model (DOM) generation using Structure from Motion - Multi-View Stereo workflow.
Image acquisition and ground control
As the name suggest, SfM-MVS is entirely dependent on images “in motion”, i.e., images taken from different viewpoints. Planning the image survey should consider several recommendations to ensure a high-quality 3D model.
There is a wide range of platforms that can be employed for the photo shooting and each of which has advantages and disadvantages that must be evaluated according to the application (Conlin et al. 2018). There are ground-based options including hand-held, the use of poles, tripods or rovers and airborne approaches using unmanned aerial vehicles (UAVs), kites, balloons and manned light aircrafts.
The images should provide a full coverage of the object or scene of interest, keeping a minimum 60% lateral and 30% vertical overlap, but these values may vary depending on the scene conditions. Camera positions should be well distributed around the object, avoiding “fan” methods (i.e., multiple images from a single point). Objects that produce low contrast require a higher percentage of overlap in order for the matches to be located and generate satisfactory results. For a feature to be digitally reconstructed, it must be observable in at least three images, so the number of images required for the reconstruction of an object or scene will then be a function of its size and the amount of overlap used.
Lighting conditions directly affect the quality of the DOM. Glare from reflective surfaces, variable contrast across a scene, the presence of shadows and changes in their length and surface albedo negatively affect point matching (Bemis et al. 2014). Ideally the survey should occur under the same light conditions. Bright cloudy days - the exterior lighting equivalent of a dome light - are recommended, since the lighting is more uniform and the casting of shadows is reduced. In some cases, the use of artificial lights may be feasible and the arrangement must be composed of main light sources of the same intensity with diffusers to ensure no visible signs of the lighting sources in the object or scene.
The occurrence of gaps, holes or distortions in the DOM usually results from the inadequate application of such parameters. Ideally, the larger the set of images generated, the greater the overlap between images and, consequently, the higher the quality of the model. However, an excessive number of images are computationally expensive, generating very large models, which makes it difficult to manipulate and post-process. Pre-processing image data is an optional step to improve overall quality and can be performed using image filters to correct color, brightness and sharpness or selecting the most adequate images from the set.
When given no reference information, the SfM-MVS generates a point cloud within a relative reference system (Westoby et al. 2012), but, for the majority of applications in geosciences, information like distance, size, volume and orientation are essential and in order to get those it is necessary to acquire ground control. When only the scale is desired, it is necessary that the distance between two points is known, which can be obtained by field measuring the distance between two markers or by adding an object of known size in the scene, such as a ruler (Verma & Bourke 2018).
For greater accuracy and full 3D referencing or georeferencing, at least three ground control points (GCPs) are required. The points should be widely distributed on the scene, avoiding linear configuration. There is a wide range of options to mark out GCP locations such as printed targets (Riquelme et al. 2017), spray paint (Viana et al. 2016), spray-painted CD (Matthews 2008) or targets (Turner et al. 2012), nails and colored flags (Haneberg 2008) or modeling clay (Jordá-Bordehore et al. 2017). The choice of the type of target must be made according to the conditions of the survey, considering that the size and the distinctiveness of the target in relation to its surroundings influence in the quality of the georeferencing. The GCPs survey is commonly done using Total Station or differential GPS, but for geological purposes great accuracy can be achieved using multiple approaches as shown by Sturzenegger and Stead (2009).
SfM-MVS workflow
There is a wide variety of SfM-MVS software, ranging from specific algorithms to stand-alone tools and web services. The commercial options include Pix4DMapper (Pix4D SA, 2017), PhotoModeler (Eos Systems Inc., 2014) and Agisoft PhotoScan (Agisoft, 2018). The latter is the most widely used in geosciences applications and the one used in this paper. Although commercial options are more user-friendly for non-experts, the main disadvantage is that their workflow is a black box, turning the identification of random and systematic errors difficult to handle (Ouédraogo et al. 2014). To get around this problem some of the open source options include Bundler (Snavely et al. 2006), PMVS (Furukawa & Ponce 2010), VisualSFM (Wu 2013, Wu et al. 2011), OpenDroneMap (OpenDroneMap 2014), Colmap (Schönberger et al. 2016, Schönberger & Frahm 2016) and MicMac (Rupnik et al. 2017).
Regardless of the software, as shown in Figure 4, the generic SfM-MVS process has around eight steps that may or may not constitute a single workflow. Ahead, we briefly describe each of the steps and algorithms commonly used in each one of them. It should be emphasized that the explanation provided here is simplified to be suitable for end users, since SfM-MVS is a combination of computer vision and traditional photogrammetry knowledge that goes beyond the scope of this work.
Given an image set, the first step is the detection of keypoints (common points between images) or feature points (sets of pixels) on single images. These points allow the different photos to be matched and the scene geometry to be reconstructed, but since the images are taken from multiple viewpoints it is a challenge to track those points. To solve this step, the scale-invariant feature transform (SIFT) object-recognition system (Lowe 1999, 2001, 2004) is the most popular approach. The performance of different region detectors is given in Mikolajczyk et al. (2005), and a comparison between other view-invariant local image descriptors is presented in Mikolajczyk & Schmid (2005).
Once keypoints are located in each image, the second step consists of finding the correspondences between the keypoints on different images. The keypoint matching is performed by identifying the nearest neighbor for each keypoint in a database containing all the keypoints identified during the first step, but there is no guarantee that any given keypoint will have a partner at another image, so the discarding of points with no good matching is required. Since the SIFT keypoint descriptor has a 128-dimensional feature vector, some search implementations can be both difficult and computationally expensive. Lowe (2004) modifies the best-bin-first algorithm (Beis & Lowe 1997) to cut off search after checking the first 200 nearest-neighbor candidates and only consider matches in which the nearest neighbor is less than 0.8 times the Euclidean distance to the second nearest-neighbor. This approach significantly increases the search speed with minimal loss in the number of correct matches and is known as approximate nearest neighbor (ANN).
Once the links between images have been established, the third step is responsible for filtering out geometrically inconsistent matches. The random sample consensus (RANSAC) method (Fischler & Bolles 1981) is the most commonly used to calculate the candidate fundamental matrices (a 3x3 matrix that “encode” the projective geometry between two views) over several iterations to filter out outliers and return the matrix with the largest number of inliers.
Using the geometrically consistent correspondences from the previous step, the fourth stage is the SfM itself, which consists of reconstructing simultaneously camera poses (position and orientation), 3D scene geometry and intrinsic camera calibration parameters. This is solved using a bundle adjustment (BA) (Brown 1958, Slama 1980), that, provided with an estimation of initial parameters values, simultaneously refines structure and motion by minimizing the re-projection error between the observed and predicted image points. The initialization of parameter values and the error minimization can be performed by several algorithms. Bundler (Snavely et al. 2006) is an example of a complete and efficient SfM system. This step produces a sparse (or coarse) point cloud and camera poses that, once georeferenced, can be used for applications (Lhuillier & Yu 2013, Fonstad et al. 2013), but most applications require a more detailed and denser point cloud, which is obtained through MVS in the following steps.
The fifth step is the point cloud georeferencing. For full 3D orientation, a minimum of three GCPs with X, Y, Z coordinates are required. The provided real world coordinates are paired with the relative coordinates derived from the previous step to derive a similarity transformation, which comprises three rotation parameters, three global translation parameters and one scaling parameter. This step can be performed on the image set at the beginning of the workflow, for the sparse point cloud or for the densified point cloud, depending on the desired result. When done at the beginning, GCPs can be used to better constrain the solution for the bundle adjustment. More information about registration methods can be found in Zitová & Flusser (2003).
After the georeferencing, the next step is optional and uses the provided GCPs to refine the parameter values obtained during the SfM step. This option is available in Agisoft PhotoScan and can improve survey accuracy by an order of magnitude (Javernick et al. 2014), but the algorithm employed by it in this step is not disclosed.
The seventh step is also optional, but it is highly recommended in projects with large number of images. Before the MVS, the image set is decomposed into overlapping image clusters by a process called clustering views for MVS (CMVS - Furukawa et al. 2010). This operation allows the reconstruction of the dense points by MVS to be done globally in the individual clusters. Software like PhotoScan allows users to manually identify these clusters (or chunks) that are then aligned (merged) into a single point cloud.
The final stage of the SfM-MVS is the multi-view stereo (MVS) algorithm, which is responsible for the production of a dense point cloud with an increase of at least two orders of magnitude compared to the sparse point cloud. Patch-based MVS (PMVS - Furukawa & Ponce 2010) is widely used and comprises three main steps: matching features, expanding patches and filtering incorrect matches. The final output is the dense point cloud.
Results and processing
After the SfM-MVS process, the user has the freedom to decide how the data will be processed and which final product will be used. Both dense and sparse clouds can be exported and used directly in a GIS (Geographic Information System) environment, interpolated into Digital Elevation Models (DEMs) or converted to a 3D surface by generating a polygon mesh (Kazhdan & Hoppe 2013). The mesh - usually a Triangulated Irregular Network (TIN) - can also receive a texture provided by the photographs (Hanusch 2008), that assigns real-world color to the digital surface. Another result of the process that can be of great value in certain applications is the generation of ortophoto mosaics.
METHOD
The on-site study was conducted under five different days on July and September 2017. A total of 60 dikes were identified, described and had their geological attitude measured with a Brunton Geo Pocket Transit Compass. For georeferencing, two fixed points were placed ∼1 km apart from each other and their coordinates obtained by post-processed static positioning using a Spectra Precision SP60 GNSS receiver, which yielded a final precision of 4 mm horizontal and 6 mm vertical. The two fixed points and 13 control points (printed markers) that were distributed on the outcrop were surveyed using a Topcon GPT-3200N reflectorless total station, which can provide a ± (3 mm + 2 ppm - D) m.s.e. accuracy (Fig. 1). All points were surveyed in UTM coordinate system (zone 23, southern hemisphere), SIRGAS2000 datum.
Weather conditions for all days of field work were of sunny, clear sky. Image acquisition was performed using two cameras, usually between 11:00 A.M.-02:00 P.M. A Nikon D7000 digital camera with a 23.6 mm × 15.6 mm CMOS sensor (4,928 × 3,264 pixels) and a 35 mm focal length lens was positioned ∼15 m from the roadcut, generating 4 m wide windows. Perpendicular and left/right oblique images were taken from 1.5 m regularly spaced spots. This camera was set to ISO 100, “aperture-priority” (AP) mode, with f/8 aperture and shutter speed determined automatically. A Nikon Coolpix AW130 using 7.8 mm and 6.1 mm focal length was used for complementary oblique images at the same spots, for whole scene capture and detail photos, set to full automatic mode. The digital models were generated with Agisoft PhotoScan professional edition (version 1.1.6). The image selection was primarily based on illumination criteria, as the outcrop is prone to shadowing. The images were masked to remove vegetation and reduce processing time. No pre-calibration or post-editing were performed.
All the dikes measured in the field were identified on the digital model. Digital sampling and the calculation of geological attitudes using ply2atti algorithm was made using the workflow described in Viana et al. (2016). Plane selection was carried out on MeshLab (Cignoni et al. 2008) in two ways:
a “punctual” measurement was made at the same locations of field survey using a 7 pixel circular brush;
“surface” measurements were made painting in the whole visible surface of the dikes (Suppl. Fig. S3).
Where the DOM was not well reconstructed (distortions and artifacts), surface sampling was not performed (Suppl. Fig. S2), as the surface distortion would significantly affect measurement results.
RESULTS
For the model generation, different quality combinations on PhotoScan settings were tested (medium/high/highest). As there is no reference model, such as a LiDAR point cloud, the quality assessment of the generated DOM was done mainly by visual inspection. Due to its more resistant composition, the dikes stand out from the surrounding rocks generating shadows depending on the direction of illumination. This shadowing effect covers surface details of the dikes and results in voids or artifacts on the digital model. To work around this problem, image sets taken at different scales and times of the day were combined to lighten some shadow areas, and this procedure has generated great improvement on the DOM quality (Suppl. Fig. S4).
The final digital outcrop was constructed from 473 images and comprises 7,524,684 vertices and 14,999,999 faces (based on a dense cloud with 51,314,241 points) (Fig. 2 and Suppl. Fig. S5). The image overlap is greater than 9 for almost all the model, georeferencing total error is 0.093 m, and the ground sampling distance (GSD) is 0.0023 m. The complete report can be seen on the Supplementary Material.
Clastic dikes are tabular bodies and as they stand out from the outcrop a box-shaped profile is expected. During the process of DOM construction, multiple settings were used on PhotoScan. In Figure 5, we compare the high quality model (the one used in this work) to one of the medium quality models that were generated during this process (using 106 images, generating a dense cloud with 30,660,551 vertices and 6,132,109 faces). We observe that the low quality DOM showed a more bell-shaped profile as a result of the surface construction. This effect is attenuated in the high-quality models, but it is not completely eliminated.
Figure 5. Digital Outcrop Models (DOMs) sections showing the difference between medium- and high-quality processing options of Agisoft PhotoScan. Sections were generated using CloudCompare (CloudCompare 2018). (A) Entire DOM showing location of inset (B) highlighted in yellow. (B) Inset of DOM showing location of sections (profiles) A-A’ and B-B’. (C) Section A-A’, high quality DOM. (D) Section B-B’, high quality DOM. (E) Section A-A’, medium quality DOM. (F) Section B-B’, medium quality DOM.
The digital surface sampling resulted in 70 measurements. Although some of the dikes that were measured in the field did not contribute to this sampling due to problems in surface generation, the increase in the number of measurements was mainly due to the fact that using the DOM it is possible to sample dikes that were inaccessible in the field.
Traditional geological compass, ply2atti (point and surface) and Turra (2009) geological attitudes were plotted on rose diagrams (Fig. 3) and stereonets (Fig. 6 and Suppl. Figs. S6, S7 and S8).
Figure 6. Stereonets: (A) poles of planes measured in the field (grey) and digital measurement in “punctual” mode (blue); (B) poles of planes measured in the field (grey) and digital measurement in “surface” mode (red). Small circles represent a ± 5º error tolerance for each measurement.
The angular deviation between dip directions and dips obtained through the traditional survey and the digital point sampling were calculated (Suppl. Tab. S1). Analyzing the angular difference between dips, 36.7% of the results are less than 5º apart, against 10% in dip directions. Increasing to 10º, 18.4% of dip directions results and 56.7% of dip results are below the threshold. For a visual comparison of the measurements with their respective errors (± 5º), small circles with a 5º radius were inserted into the stereonets (Fig. 6).
DISCUSSION AND CONCLUSIONS
Due to the great flexibility of SfM-MVS, it is necessary to emphasize that each application of the technique presents different difficulties and/or limitations. Since the studied outcrop is located in a dual carriage highway with heavy traffic, the constant activity of passing cars and trucks slowed down the positioning and surveying of GCPs. The terrain geometry and safety procedures constrained the access to the outcrop in terms of distance and viewpoints for image acquisition; given the desired level of detail for the DOM, the number of images obtained was high, consuming a considerable amount of storage memory.
The difference between the number of measurements taken in this work in relation to Turra (2009) also shows in the statistics, since we did not reconstruct the whole outcrop and that some dikes are now inaccessible or covered by vegetation. Due to this difference in the amount of measurements, some variation in the statistical analysis, also reflected in the rose diagrams, is expected. However, we can observe that the NNW preferential direction observed in the outcrop remains, although there is a certain NNE variation present.
Comparing the measurements obtained in the field activity of this work with the punctual ones obtained by ply2atti, a certain variation is observable, mainly on dip directions (Fig. 6). This factor can be related to field practices, which do not necessarily provide an accurate measurement due to misuse of the compass, or caused by manual adjustment of the plane, but it can also be explained by the deviation of the walls of the dikes on the DOM that is reflected in the profiles of Figure 5.
Since the walls of the dikes present roughness and variable degree of undulation, a single measurement performed with magnetic compass may not represent the best-fit plane. Ply2atti was created to provide an average geological attitude based on hundreds to millions of points on the surface, so the best practice would be to select the entire side of the dike leading to the best possible adjustment, as done by the “surface” digital sampling. However, as mentioned earlier, voids and artifacts on the digital model may segment or distort these surfaces, making them unreliable for this type of sampling. Cawood et al. (2017) describe these distortions and voids caused by occlusion during sampling and emphasize that this is an effect of the characteristic morphology of the area; to work around this problem, the authors used an UAV to provide the camera positions and angles to fully reconstruct the outcrop. A careful analysis of the study area should consider the geometry of the features of interest and more than one source for the complete imaging of the outcrop whenever possible.
According to the goals established for the project, it is possible to conclude that the objectives were reached, although the case addressed does not represent a simple application for the chosen techniques, due to the lithological and structural complexity of the outcrop.
Three-dimensional reconstruction with SfM-MVS was successfully performed. However, it can still be improved. A study on the combination of the following factors can provide answers on this question: resolution of the photographs, area of overlap, imaging geometry (perpendicular to the outcrop or convergent) and influence of the direction of illumination.
