The Ising model and real magnetic materials

The Ising model and real magnetic materials

W. P. Wolf

Yale University, Department of Applied Physics,

P.O. Box 208284, New Haven, Connecticut 06520-8284, U.S.A.

Received on 3 August, 2000

The factors that make certain magnetic materials behave similarly to corresponding Ising models are reviewed. Examples of extensively studied materials include Dy(C

₂

H

₅

SO

₄

)

₃

.9H

₂

) (DyES), Dy

₃

Al

₅

O

₁₂

(DyAlG), DyPO

₄

, Dy

₂

Ti

₂

O

₇

, LiTbF

₄

, K

₂

CoF

₄

, and Rb

₂

CoF

₄

. Various comparisons between theory and experiment for these materials are examined. The agreement is found to be generally very good, even when there are clear differences between the ideal Ising model and the real materials. In a number of experiments behavior has been observed that requires extensions of the usual Ising model. These include the effects of long range magnetic dipole interactions, competing interaction effects in field-induced phase transitions, induced staggered field effects and frustration effects, and dynamic effects. The results show that the Ising model and real magnetic materials have provided an unusually rich and productive field for the interaction between theory and experiment over the past 40 years.

I Introduction

For many years the Ising model and its variants were re- garded as theoretical simplifications, designed to model the essential aspects of cooperative systems, but without detailed correspondence to specific materials. In the early 1950's pure rare earth elements became more readily available and this stimulated the study of new magnetic materials. Some of these were soon recognized as close approximations to the Ising model. We will review the similarities and differences between theoretical Ising models and a number of real magnetic materials.

The early experiments were aimed at identitying Ising-like materials and characterizing the parameters of the microscopic Hamiltonian. Various approximate calculations were then compared with thermodynamic measurements. It was soon recognized that there are some essential differences between the models and real magnetic materials, but the overall agreement was found to be generally very satisfactory. The advent of theoretical predictions of critical point behavior led to comparisons of critical exponents and amplitudes, and again generally satisfactory agreement was found. The recognition that Ising-like behavior very close to critical points may also be found in systems that have large non-Ising interactions significantly increased the number of materials that could be used for such studies.

The materials that order antiferromagnetically offer additional opportunities for comparing theory with experiment. Field-induced phase transitions of both first and second order were found, with crossover regions near tricritical points. Experimental studies of tricritical points are difficult due to practical complications, but generally good agreement with theory was again found. Experiments also gave evidence for phenomena not envisaged by simple Ising models. One of these was the possibility of coupling to the staggered magnetization in antifferromagnets, and differentiating between the two time-reversed antifferromagnetic states. Most recently systems in which interactions between the spins are frustrated have been studied.

In all of this work the interaction between theory and experiment has been crucial, and each has stimulated the other. Indeed, one can speak of "layers of understanding," as each has advanced predicted and observed behavior in turn. If there is one lesson to be learned it is that both theory and experiment have to be treated with some healthy skepticism if one is seeking true understanding of real materials.

II Model materials

In order to identify materials with an Ising-like microscopic Hamiltonian, one needs to understand the behavior of individual magnetic ions in a crystalline environment. The basis for this understanding comes from the early work of Van Vleck, as refined with the advent of paramagnetic resonance in the 1950's and the introduction of the spin Hamiltonian [1].

For a material to be Ising-like two conditions must be met. First, the ground state of the ion must be a doublet well separated from excited states (DE >> k_BT_C). Ideally, the doublet should have "Kramers" degeneracy corresponding to an odd number of electrons in the ion, and most of the materials studied have satisfied this criterion. Ions with an even number of electrons can also have doubly degenerate states, if the symmetry is sufficiently high, but any small change in symmetry will split the doublet. Such a splitting may be small or large on the scale of other effects, but it is often simply ignored. In practice, it is much safer to stay with ions that are subject to Kramers time reversal symmetry, that is ions with an odd number of electrons.

The second condition involves the quantum mechanical description of the two ionic states. The important criterion is that all matrix elements coupling the two states of each of the interacting ions should vanish for all of the operators involved in the spin-spin interactions. In practice, the most usual interactions involve exchange and dipolar couplings, both of which involve operators that transform as vectors, e.g. JS_j.S_j. For such operators the selection rule is Dm = 0, ±1, where m is any angular momentum quantum number. In principle one can also have interactions involving higher rank tensors, such as anisotropic exchange or quadrupole-quadrupole coupling,[2] and to exclude these as well one needs to find doublet states in which such interactions also have no matrix elements between the two states.

Suitable cases have been found in many rare earth compounds. The first such material to be identified as "Ising-like" was Dy(C₂H₅SO₄)₃.9H₂0, dysprosium ethyl sulfate (DyES).[3] An analysis of the crystal field by Elliott and Stevens,[4] using results of earlier magnetic and optical rotation measurements,[5] had shown that the ground state is a Kramers doublet described primarily as |J = 15/2, J_z = ±9/2 > with small admixtures of |J = 15/2, J_z = 3/2 > and |J = 15/2, J_z = 15/2 > . For such a doublet only operators involving tensors of rank 3, or greater, will have matrix elements between the states, and no such operators are involved in any of the usual exchange and magnetic dipole interactions. Therefore one could conclude that in this material the microscopic interaction Hamiltonian could be accurately represented by the Ising form

where s_zi and s_zj = ±1, and the sum i > j runs over all pairs of interacting sites i and j. A discussion of more general situations can be found in Ref. 2.

In the specific case of DyES the local Ising axes were all parallel, and also parallel to the hexagonal crystal axis, but it should be pointed out that this need not always be the case. The Ising form for the interaction is the result of the local anisotropy, the axis of which is determined by the point symmetry at the site of each ion. As we shall see, some of the most interesting situations arise from the very fact that the localising axes are not always parallel.

Table I shows a selection of Ising-like materials that have been studied extensively over the past 40 years. In this paper we will discuss some of the specific aspects that have made these materials of interest. Many other Ising-like materials have, of course, been studid, and extensive references to these and other compounds may be found in the reviews by de Jongh and Miedema, [6] and by Stryjewski and Giordano.[7]

A. Strength of the Interactions

There is no quantitative theory for calculating strength of the various interactions from first principles, and the coupling constants K_ij must therefore be determined experimentally for each material. The magnitudes are generally quite weak in the materials that have been studied, and since all magnetic ions interact through magnetic dipole-dipole coupling we can write, without any loss of generality, K_ij = D_ij (1+ a_ij), where D_ij denotes the magnetic coupling. This can be calculated from the experimentally determined magnetic moments of the interacting ions and their relative positions. One would normally expect the a_ij to be significant only for near neighbors, and this generally turns out to be the case, though in some cases the range of significant non-dipolar interactions can extend out to third nearest neighbors.[8] Also, both positive and negative non-dipolar interactions have been found, and in practice one must be careful to check for such possibilities.

It is tempting to ignore such complications because it is not easy to determine several a_ij in every case, but non-dipolar interactions beyond nearest neighbors should always be considered as a possibility.

To find the interaction constants, one must fit experimental data to theoretical expressions for thermodynamic quantities (usually the susceptibility or specific heat) in regions where the theory is asymptotically exact. In practice this usually means T >> T_C or T << T_C, where T_c is the critical temperature. For example, the susceptibility for T >> T_C can be fitted to the asymptotically exact expression [9, 10]

where

while the specific heat can be fitted to

where

It should be noted that fitting data in regions far from the critical point implies looking for very small deviations from ideal behavior. Great care must be taken to avoid systematic errors from extraneous effects such as contributions from excited states, Van Vleck temperature independent susceptibility or small systematic errors. For the specific heat corrections for lattice contributions and nuclear hyperfine interaction must also be made.

In a very dilute material such as DyES one might expect non-dipolar interactions to be very weak and that is indeed what was found [11]. The very first Ising-like magnet was thus also the first purely dipolar ferromagnet, though the significance of that distinction did not become apparent until much later,[12] after critical point theory had been developed and after the importance of marginal dimensionality had been recognized.

B. Approximate Theories

The earliest experiments were compared against Ising model theory using various approximations including mean field, cluster models, combinations of exact linear chain results with mean field, and series expansions, both at low and high temperatures. Two early examples [13] for quasi one-dimensional DyES are shown in Figs. 1 and 2 The agreement with even very simple approximations is good, especially in light of the fact that there are no adjustable constants.

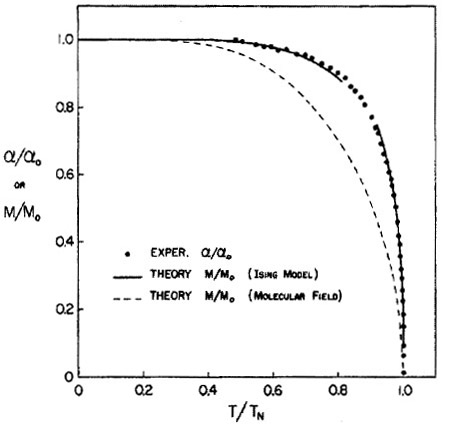
The development of long power series expansions for both low and high temperatures during the 1960's [14, 15] made it possible to compare magnetic and thermal measurements over much wider temperature ranges, including the critical regions. One material that yielded excellent results was DyPO₄ and examples [16, 17] are shown in Figs. 3, 4, and ⁵.

It can be seen that the agreement is very good, especially in light of the fact that the theory contains only one adjustable parameter, the nearest neighbor interaction. However, the success of these comparisons depended on some special factors that are worth discussing.

First, the choice of material turned out to be very important because the model calculations could be performed readily only for relatively simple lattices. The fact that DyPO₄ closely approximates a simple diamond lattice was essential for a detailed comparison with available series. On the other hand, since the theoretical series expansions are extremely time consuming they were able to consider only nearest neighbor interactions and thus ignored any effects from longer-range interactions. The excellent agreement between theory and experiment was, therefore, to some extent fortuitous, though it can be argued that more distant neighbor interactions, while present, can cancel in their effect. However, the overall agreement clearly demonstrates the close relation between to Ising model and this material, even though later studies revealed complications that are still not completely understood [18, 19].

An extension of these comparisons became possible with the discovery of materials in which the lattice structure strongly favored interactions within a plane of spins, with almost no interaction between planes. Such materials would be expected to behave as quasi two dimensional systems and, if the Ising criteria could also be satisfied, would provide an opportunity to compare experimental data with the exact results on the two dimensional Ising model. No rare earth materials with such structures had been found but several metal fluorides involving transition metals were identified in the late 1960's. Because of strong crystal field quenching most transition metal ions show relatively little anisotropy and behave more as Heisenberg systems. The exception is the Co ion, which is well known to show considerable anisotropy in many materials.[20]

Two very similar materials identified as both two- dimensional and Ising-like were K₂CoF₄ and Rb₂CoF₄, [21] and in Figs. 6 and 7 we show the susceptibility [6] and the specific heat, [22] compared with the two dimensional Ising model with one adjustable constant. It can be seen that the agreement is very good. However, a number of complications must be noted that show again that care must be exercised in comparing theory with experiment in these cases.

Figure 8.
Magnetic susceptibility as a function of temperature for K₂CoF₄, without any corrections. Note the differences from Fig. 6 and the large susceptibility perpendicular to the axis reflecting the influence of low-lying states and corresponding deviations from the simple Ising Hamiltonian. After Ref. 21.

For the susceptibility, we see in Fig. 8 that the measured value [14] is, in fact, much larger than that shown in Fig. 6, which has been corrected empirically by subtracting a contribution from Van Vleck temperature independent paramagnetism to allow for the presence of low-lying excited states. It can be seen that the correction is very large, and it is clear that the correction for the presence of excited states will not really be isotropic and independent of temperature, as assumed. This probably accounts for the observed differences at the highest temperatures. [6]

For the specific heat comparison with Onsager's exact two-dimensional solution another factor must be noted. Neutron scattering experiments [23] had shown that the non-Ising interactions in this material are, in fact, quite significant, amounting to some 55% of the Ising terms, but it would appear from the close agreement that this makes very little difference.

The conclusion to be drawn from these comparisons is that even rather large differences between the model Hamiltonian and the real Hamiltonian can leave the agreement between theory and experiment relatively unaffected. The dominance of the Ising terms in the immediate vicinity of the critical point in these, and in even more isotropic materials, can be understood in terms of crossover effects.

Overall the agreement found between the approximate theories and experiment was very satistactory, and it encouraged both theorists and experimentalists to intensify the study of critical point properties.

C. Critical Points

Using various analytical techniques, the high and low temperature series expansions could be extrapolated to locate the critical point, and estimate the values of thermodynamic properties at the critical temperature. Table II, adapted from Ref. 6, shows a selected comparison. It can be seen that the general agreement is again very satisfactory, and one can certainly conclude that suitably selected magnetic materials are well explained by Ising model calculations.

TABLE II.
Critical entropy and energy parameters^a

a after Ref. 6 and refferences contained therein. b number of nearest neighbors.

D. Critical Exponents

The great strides in theoretical understanding of critical phenomena in the 1960's and 1970's led to predictions of many critical exponents and scaling relations between them. Many of these have been tested by measurements on Ising-like magnets. We will review the story of just one of these exponents, the specific heat exponent a for the antiferromagnet Dy₃Al₅)₁₂, dysprosium aluminum garnet (DyAG), which will illustrate the delicate interaction between theory and experiment in these studies. It will emphasize the care and skepticism that must be exercised in studies of this kind before any definite "proof" can be claimed.

The first specitic heat measurements [24] are shown in Fig.9. They illustrated dramatically the failure of mean field theory, even though mean field theory is asymptotically exact at low temperatures for an Ising-like system such as DyAG. They also provided clear evidence that critical point behavior is quite singular, reminiscent of Onsager's result for the two- dimensional Ising model.

To study the critical point behavior more closely a series of high resolution measurements were made,[25, 26] and one set is shown in Fig. 10.

Inspired by the 2D Ising model, an attempt was made to fit the specific heat to a logarithmic singularity of the form

and for T < T_C an apparent fit was found. However, for T > T_C a logarithmic fit was clearly ruled out by the data, so a fit to the (now commonly accepted) form

was tried, with amplitudes A₊ and B₊, the critical temperature T_c, and the exponent a all allowed to vary treely. The fit was quite good, but the value obtained for a = 0.31 ± 0.02 was well outside the predictions of theory, which were converging on a = 0.125, and the values obtained for the amplitudes did not agree with theory. Moreover, the logarithmic form for T < T_c was also in conflict with theory, which predicted similar forms above and below T_c.

It was pointed out by Gaunt and Domb [27] that the asymptotic singularity predicted by the theory for T < T_c was, in fact, valid only extremely close to T_c, and would not be observable even with the relatively high resolution of data such as in Fig. 10. They constructed an interpolation expression that combined the asymptotic form with the low temperature series, and showed that for T < T_c the apparent variation is indeed similar to a logarithmic singularity.

A re-examination of the region T > T_c next revealed [26] the striking fact that a very small change in the choice of T_c resulted in very large changes in the values of the other fitted parameters. Table III shows some of the results. It became clear that simply fitting data to a theoretical expression could lead to very misleading results. Moreover, there is a very strong correlation between the various fitted constants, so that it was not meaningful to look for a fit to only the exponent. [28]

A more careful fit of the data, using least-squares-cubic splines with knots, [29] resulted in a value for a = 0.12 ± 0.03, now in excellent agreement with the theoretical value.

One problem with all fits to critical point predictions is the fact that the asymptotic range is generally very narrow, and is limited by "rounding effects" that inevitably broaden any singularity. To extend the range over which the asymptotic form can be fitted one can include so-called "corrections to scaling," whose leading term will modify the expression for the specific heat to the form

where t = |(T - T_c)/T_c|. It is clearly impossible to fit all the eleven parameters in this expression without some constraints, and Rives and Landau [30] chose to set a₊ = a_- = 0.125, B₊ = B_-, and x₊ = x_-, as predicted by theory. With these constraints it was then possible to fit the data over relatively wide ranges of temperature both above and below T_c.

Figure 10.
Specific heat of Dy₃Al₅O₁₂ as a function of temperature near T_N, under four decades of temperature resolution. Temperatures are measured relative to an arbitrarily chosen T_max = 2.544 K. After Ref. 26.

Critical exponents and amplitudes describing the singularities of other thermodynamic quantities tend to be somewhat easier to determine, since they are generally stronger than that for the specific heat. Many such exponents and amplitudes have now been measured for both Ising-like and Heisenberg-like materials, and one can certainly conclude that theory and experiment are in agreement.

However, the history of the different attempts to fit data to the theory illustrates some general principles that are sometimes ignored. It is clear that both theoretical understanding and the measurement and analysis of experimental data tend to improve over time. One must be very careful, therefore before one can claim that an experiment has "proved" the theory, and it is much sater to say that the experiment is consistent with the theory within specified physical assumptions, as well as a measure of the quality of the statistical fit. Such a conclusion is not limited to the analysis of critical point data, of course, but in this field there is a particularly rich history of successive attempts to verify theory.

III Extensions of the simple Ising models

So far we have discussed observations that were consistent with the Ising model as usually discussed and, as we have seen, materials have been found that closely reproduce many theoretical predictions. However, on occasion observations are made that differ qualitatively from the standard theory and demand that extensions of the simple models. Several of these have led to interesting new physics.

A. Magnetic dipole interaction

Magnetic dipole interactions are, of course, present in all magnetic materials but it is difficult to include them in most model calculations because they are of long range. Many of the Ising-like materials that have been studied in fact have relatively weak non-dipolar interactions, so that considering only the near neighbors might not turn out to be a very good approximation. In some situations the interactions with more distant neighbors tend to cancel, but in some cases they cannot be ignored.

1. Shape Dependence

The most obvious situation in which dipole interactions are evident is in the shape dependence of the magnetic susceptibility. Shape dependence is usually discussed in terms of a classical demagnetizing factor, N, that relates the susceptibility for a given shape c_N to that of a long needle-shaped sample c_{N = 0} to through the expression

TABLE III.
Critical exponents and amplitudes for Dy₃Al₅O₁₂ for T > T_N, showing the effect of choosing different values for T_N, together with theoretical estimates for three cubic Ising models.

a Temperatures measured relative to Tmax = 2.543 ± 0.10K. bTN estimated trom measurements below + Tmax and Eq.4. c After Ref. 28 and refferences contained therein. d Using methods described in Ref. 29. e After Ref. 30, with TN fitted and a fixed at the theoretical value.

This relation depends only on the assumption that the sample is magnetized uniformly, which is generally the case for ellipsoidal sample shaped samples. An illustration of this effect is shown in Fig. 11.[31]

In the paramagnetic phase the shape dependence is not a serious problem, though the quantitative effect can be quite large. The question then arises whether there is one particular shape that is more "intrinsic," in that it corresponds most closely to the simple near-neighbor model. Unfortunately the most obvious answer, the long thin needle-shape with N = 0, for which the internal field is the same as the applied field, does not approximate to that case. For that shape the cumulative effects of the long-range dipolar interactions are, in fact, maximized and provide a significant non-zero internal field. An alternative possibility is to correct to a shape for which the long-range dipolar field vanishes,[32] but this is only a mean-field correction.

Below the critical temperature the effect of the dipolar interactions can be even more significant. If the ordering is ferromagnetic, c_{N = 0} diverges at T_c and the measured susceptibility is then governed entirely by the demagnetizing factor. This is the case for the measurements shown in Fig. 11. The effective value of N can then be estimated from the measured value of 1/c, but errors can be very large if the sample is not shaped accurately into an ellipsoid. In the ordered state the dipolar interactions will cause a ferromagnet to break up into domains so as to lower the magnetostatic energy [33]. The formation of domains is anticipated by corresponding fluctuations in the paramagnetic region that have been studied extensively using neutron scattering [34, 35].

Figure 11.
The reciprocal susceptibility parallel to the crystal c-axis as a function of temperature for LiHoF₄. The experimental points correspond to measurements for five different sample shapes, characterized by demagnetizing factors, N. The constant values for T < 1.5 K correspond to a transition to the ferromagnetic state, for which 1/c_{N = 0} = 0. After Ref.31.

For antiferromagnets the effect of dipolar interactions is less significant because susceptibilities are finite but, as we shall see below (see Sec. IIIB), domains can also be formed at first order phase transitions.

2. Critical properties

Long-range dipolar interactions also have a dramatic effect on the critical properties of dipolar Ising ferromagnets. Theoretical models based not on a microscopic model but on perturbation and renormalization group ideas predicted [36, 37] that a dipolar Ising (n = 1) ferromagnet will have a marginal dimensionality d^* = 3, and hence exhibit critical point properties described by Landau (mean field) theory with logarithmic corrections. Thus, for example, the susceptibility, c, spontaneous magnetization, M_s, and specific heat, C, are predicted to vary as

where t = T - T_c/T_c as before, and t_o^x and t^c₀ are constants. Extensive experiments on LiTbF₄,[38-47] and on DyES [42] have shown that these predictions are consistent with the data, and have provided elegant insight into the unique critical properties of these Ising systems. As discussed before, it is very difficult to prove that certain critical point exponents have the values predicted by the theory, but careful experiments have provided convincing evidence that these systems do indeed behave quite differently from Ising systems with predominantly short-range interactions.

B. Field-induced phase transitions

Ising-like antiferromagnets have provided additional phenomena not anticipated by the usual simple Ising models. The application of a magnetic field would be expected to destroy the antiferromagnetic order but the details of the transition have shown some surprises.

1. First order transitions

Conventional wisdom had predicted that the effect of a magnetic field would be a simple shift of the second order phase transition to lower temperatures as the field is increased. The phase diagram would be as shown in Fig. 12a. At T = 0 K the transition would become first order, corresponding to a simple reversal of the spins opposed to the magnetic field. Detailed support for such a prediction was provided by a two-dimensional superexchange Ising model devised by Fisher [48] that could be solved exactly in terms ot the zero field Ising model. The results for the magnetization of the model are shown in Fig. 13.

The first experiments on the Ising-like antiferromagnet DyAG gave results in sharp contrast to these predictions [49]. Magnetization isotherms for fields applied along a [111] direction are shown in Fig. 14a. It can be seen that there appear to be no singularities at any field, but there are large regions at the lowest temperatures in which the magnetization appears to vary linearly.

A part of the puzzle was resolved when the data were re-plotted as a function of the internal field, corresponding to a measurement on a long thin needle sample shape. These results are shown in Fig. 14b. It can now be seen that the low temperature transitions are essentially discontinuous in the magnetization, corresponding to a first order transition. The nature of the transition as a function of applied field was discussed by Wyatt [50] in terms of domains similar to those in Ising-like ferromagnets. The domains were later observed optically by Dillon et al. [51]

Figure 12.
Possible phase diagrams in the field-temperature plane for antiferromagnets. (a) usual phase diagram with nearest neighbor interactions, in which the antiferromagnetic phase (A) is separated from the paramagnetic phase (P) by a line of second order transitions. (b) phase diagram with competing interactions, in which there are both first order and second order transitions, and a tricritical point where they meet. (c) shows the phase diagram when there is a coupling between the applied field and the antiferromagnetic order parameter. In this case there is only a first order transition ending in a critical point. (d) same as (c) but showing both positive and negative applied fields. The positive field induces one of the two antiferromagnetic states, A⁺, while the opposite field induces the time-reversed state A^-. The phases A⁺ and A^- are separated by a first order line that ends at the Néel point T_N. In DyAlG cases (b), (c), and (d) are observed under different conditions.

Figure 13.
The magnetization as a function of magnetic field at fixed temperature for a two-dimensional super-exchange antiferromagnet. The dashed curve is the locus of transition points. The curves are labeled by appropriate values of the reduced temperature. Note the continuity of all curves except for zero temperature, and the infinite derivative at the transition points. After Ref. 48.

The origin of the first order transition at low temperatures could be explained by the fact that the interactions in DyAG are not limited to nearest neighbors, as commonly assumed in simple models. In fact, there are competing ferromagnetic and antiferromagnetic interactions involving first, second and third nearest neighbors. [8] The relative strengths of these interactions are shown in Table IV. With competing interactions, first order transitions are not unexpected, as predicted by simple mean field models [52].

TABLE IV.
Spin-spin interactions in Dy₃Al₅O₁₂^a, showing the relative importance of several shells of near neighbors. Similar competing terms may be expected in many other materials, but are often not considered.

2. Induced staggered fields

With the first order transition at low temperatures now understood, we are still left with the unexpected behavior at higher temperatures, which certainly did not appear to correspond to a second order transition with a singularity in the derivative of the magnetization, as in the exact model (Fig. 13). Thus, instead of a phase diagram as in Fig. 12b, it appeared that there was only a "higher order" transition, or as it later turned out, no transition at all, between the end of the first order phase boundary and the Néel point. The corresponding phase diagram is shown in Fig. 12c.

Figure 14.
The magnetization of a spherical sample of DyAlG as a function of field along [111] at temperatures above and below the Néel temperature. In (a) the magnetization is plotted as a function of the externally applied field. In (b) the magnetization is plotted as a function of the internal field, calculated by H_int = H_ext- NM, with N = 4p/3 for a sphere. After Ref. 49.

The reason for this puzzling situation was not resolved until 1974 when Blume et al. [53, 54] noted that DyAG happens to have a somewhat unusual lattice structure, whose symmetry allows a coupling between the applied field and the antiferromagnetic order parameter. In most antiferromagnets such a coupling is not allowed, because the antiferromagnetic order must usually be indexed on a unit cell bigger than the chemical unit cell, and is thus not translationally invariant, in contrast to the magnetic field whose components are, of course, translationally invariant.

In the garnet structure the coupling between the magnetic field and the antiferromagnetic order parameter, h, takes the form of an additional term in the free energy DF ~ hH_xH_yH_z, where H_x, H_y, and H_z are the components of the applied field along the cubic axes. In the presence of such a term an applied field will couple to the antiferromagnetic order and destroy any continuous phase transition. Evidence for this was found in a neutron scattering experiment, results of which are shown in Fig. 15a.

The symmetry argument thus explained the absence of a second order phase transition, but it did not suggest a physical mechanism that would result in such an extra term in the energy. The answer was found, surprisingly, to lie in a combination of two quite normal teatures of DyAG: the symmetry of the garnet lattice structure and Ising character of the local spins.

Figure 15.
Results for the staggered magnetization, M_s, for DyAlG as a function of the internal field with H_i|| [111]. (a) Experimental results of Blume et al. [Ref. 53]; (b) results of the cluster calculation for the same value of T/T_N. After Ref. 55.

Fig. 16 shows, for simplicity, half the sites in one unit cell of DyAlG, together with the signs of the nearest neighbor interactions due to the dominant magnetic dipole forces. (The remaining sites are related by simple translations and share no nearest neighbor bonds with the others.) It can be seen that half the nearest neighbor interactions are shown as ferromagnetic and half are antiferromagnetic, but in an unusual pattern.

Figure 16.
Lattice and bond structure of the staggered interaction model shown in a [001] projection. The structure is body centered cubic, with 6 sites in the primitive unit cell. The figure shows the conventional unit cell. The numbers give the heights above the z = 0 plane in terms of the unit-cell edge length. Ferromagnetic bonds are shown as solid lines and antiferromagnetic bonds are shown as broken lines. Note that only half the sites, marked as (·), form triangles with three ferromagnetic bonds, whereas the sites marked (o) have only two ferromagnetic bonds. The structure shown corresponds to one half of the sites in DyAlG. The omitted sites form a similar lattice related by simple translations and do not share any nearest neighbor bonds with the sites shown. After Ref.55.

This comes about from the fact that the local Ising axes point in different directions, as demanded by the garnet symmetry, and it is then necessary to specify a common set of crystal axes to describe the interactions between neighbors. Two spins can be said to be "ferromagnetically aligned" relative to an applied field if they both point along a positive (or both along a negative) crystal axis, and antiferromagnetically aligned if one points along a positive crystal axis and the other along a negative crystal axis. Physically this simply reflects the result of projecting the usual magnetic dipole-dipole interaction

along orthogonal axes. For example, if m_i is constrained to the x-axis and m_j along the y-axis the interaction will reduce to the form

where x_ij, y_ij and r_ij are the relative positions of m_i and m_j. It is clear that this will change sign between two neighbors one at +y and one at -y, for the same x.

Given the arrangement of interactions shown in Fig. 16 one can then use all the usual techniques to study the properties of such an Ising model. So far very little seems to have been done in this direction, and the only consideration of the properties of such a model seems to have been given by Giordano and Wolf, [55] who studied the leading terms in the low temperature series for the energy.

They showed that in the presence of a magnetic field with components along all three axes, the energy of excitation of three spins will not be the same for the "positive" and "negative" sublattices, so that the magnetic field does indeed couple to the antiferromagnetic order parameter. The effect on the order parameter is shown in Fig. ISb. It can be seen that there is no visible boundary between the "ordered" and the "paramagnetic" phases, and the usual second order phase transition therefore disappears.

It would seem to be of some interest to study the "staggered interaction" model shown in Fig. 16 with more sophisticated techniques, since it has a phase diagram similar to that of a liquid-gas system. The first order line separating the antiferromagnetic and paramagnetic phases ends in a simple critical point, as shown in Fig. 12c. A somewhat similar phase diagram has recently been proposed in connection frustrated spin ice systems. (See Sec. IIIC.)

If positive and negative fields are included, the phase diagram of the staggered interaction model becomes even richer, in that the two time-reversed antiferromagnetic states A⁺ and A^- are separated by another first order line, as shown in Fig. 12d. Even more complicated phase diagrams are possible if the strict Ising conditions are relaxed [55].

The ability to couple directly to the antiferromagnetic order parameter leads to the possibility of observing and manipulating the two time reversed antiferromagnetic states A⁺ and A^-, and a number of interesting optical and magnetoelastic experiments have been reported. Because of lack of space, we shall not discuss the details here, which can be found in Refs. [51-61].

3. Tricritical points

Materials with a more conventional phase diagram, such as in Fig. 12b, have a tricritical point, where the first and second order phase boundaries meet. Extensive efforts have been made to study such points, but it turns out that there are experimental difficulties that make it even harder to extract exponents than at critical points. We shall not discuss the details here, but refer to a review of the problems and successes [62].

The ability to apply staggered fields in suitable cases makes it possible to study the so-called "wings" near tricritical points [63,64] and, subject to some experimental limitations, good agreement with theoretical predictions was found. This is a field in which additional experiments would be welcome.

C. Frustration effects

The effect of non-collinear Ising axes has recently received much attention in connection with anomalous properties observed for some rare earth titanates with the pyrochlore structure. The structure of the rare earth ions is shown in Fig. 17a. Each spin has six nearest neighbors, three belonging to each of two linked tetrahedra. The local symmetry axis at each spin site points towards the center of its tetrahedron, as shown in Fig. 17b.

It was first noted by Harris et al. [65] that a ferromagnetic coupling between nearest neighbors in this structure (as constrained by the Ising axis at each site) would lead to frustration. The relation between the pyrochlore structure and the Ising model has also been discussed by Moessner [66] and by Bramwell and Harris [67]. It turns out that it is not possible to satisfy more than half of the nearest neighbor bonds in each tetrahedron, and the state with the lowest energy can be de- scribed as "two in" and "two out." That is, two spins point towards the center while two point away from the center. There are many ways to achieve such an arrangement, and the ground state is, therefore, highly degenerate.

It was pointed out by Harris et al.[65] that such a ground state is directly comparable with the model proposed by Pauling [68] to account for the anomalous entropy of ice, and they coined the expression 'spin ice' for materials of this kind. In Pauling's model the protons belonging to the H₂0 molecules are displaced so that they are either closer or further from their oxygen atom. Given the tetrahedral structure of ice, it is only possible to displace two of the four protons in the same sense for each tetrahedron, leading to the ice rule "two in, two out," as illustrated in Fig. 17c.

Specifically, Harris et al. had suggested that Ho₂Ti₂0₇ should be a spin ice, but this conclusion has been subject to some discussion. It turns out that the specific heat of Ho₂Ti₂0₇ is quite anomalous, in that it suddenly becomes impossible to measure because the equilibrium time becomes very long [69]. It is not clear if this signifies a transition to some sort of partially ordered state or if it is a result of spin ice frustrations. At the same time some, but not all, Monte Carlo simulations have suggested that Ho₂Ti₂0₇ was indeed a spin ice [70]. Further work is needed to resolve the question.

On the other hand, there seems to be no doubt that the isostructural Dy₂Ti₂O₇ pyrochlore does behave as a spin ice, and two different computer simulations [70, 71] have been able to reproduce the experimental results over a wide range of temperatures. The results of one of these is shown in Fig. 18a.

Figure 17.
(a) A schematic representation of the pyrochlore lattice, showing the positions of the magnetic ions. (b) The ground state of a single tetrahedron of spins coupled ferromagnetically with local Ising anisotropy. (c) Local proton arrangement in ice, showing the oxygen atoms (·) and hydrogen atoms (-), and with the displacement of the hydrogen atoms trom the mid-points of the oxygen-oxygen bonds marked by arrows. The similarity to (b) has led to the concept of 'spin-ice.' After Refs. 67 and 73.

The striking feature of this behavior is the fact that the total entropy associated with the ordering process is less than R ln2, as is otherwise observed in all other systems with two-fold degenerate ground states. The entropy as a function of temperature is shown in Fig 18b. It can be seen that it extrapolates close to the value R(ln 2-1/2 ln 3/2) predicted for ice by Pauling [68].

It is interesting to note that the anomalously low value for the entropy was first noted some 30 years ago [72] but, at the time, it was ascribed to incomplete measurements, and no further study was made. It is tempting to speculate how the field of frustration might have advanced if the anomaly had been confirmed experimentally.

To provide further insight, and to verify that the reduced entropy is not simply the result of experimental error, or possible lack of stoichiometry, Ramirez et al. also measured the specific heat in magnetic fields [71]. The application of a field would be expected to reduce the degree of frustration and thereby increase the total entropy. The results for a field of 0.5T are shown in Fig. 18b. It can be seen that the entropy is indeed increased and that it now tends towards a value closer to the usual R ln2 for a system with a doublet ground state.

However, the application of even stronger magnetic fields produced some unexpected effects in addition, and these are shown in Fig. 19. Three sharp peaks in the specific heat are now observed on top of the broader peak and, quite surprisingly, they are found to be independent of the strength of the field. The entropy associated with these peaks is quite small, so that only a fraction of the spins appear to be involved.

Figure 18.
Specific heat and entropy of Dy₂Ti₂O₇ and Pauling's prediction for ice. (a) Specific heat divided by temperature for H=0 (o) and H=0.5T (·). The dashed line is a Monte Carlo simulation of the zero-field C(T)/T. (b) Entropy of Dy₂Ti₂O₇ found by integrating C/T trom 0.2 to 14K. The value of R(ln2-1/2 ln3/2) is that found for ice (I_h), and ln2 is the usual full spin entropy. After Ref. 71.

There is no detailed understanding of these effects, but a possible explanation may involve the ordering of spins with axes perpendicular to the magnetic field made possible by the ordering of the remaining spins by the field [65, 73]. A somewhat similar phenomenon had previously been observed in crystals of DyAG [74]. In the present case the situation is complicated by the fact that the measurements were made on powdered samples and experiments on single crystals would clearly be desirable.

One interesting feature of the study of the pyrochlores is the fact that most of the "theory," so far, has involved computer simulations. Such simulations are not easy because long-range dipole interactions are important in these systems, and there has been some disagreement over the approximations.[70, 71] It would be helpful to supplement the simulations by analytical results. This is clearly a challenging new extension for Ising model studies.

Figure 19.
Specific heat as a function of temperature for Dy₂Ti₂O₇ in various applied fields. The broad H = 0 feature is suppressed on increasing H and replaced by three sharp features at 0.34, 0.47 and 1.12K. Inset (a) shows the constancy of these transition temperatures with field. Inset (b) shows the result of finite-field Monte Carlo simulations of C/T. After Ref. 71.

D. Dynamic effects

Both the theory and experiments concerning Ising-like systems have concentrated on static equilibnum properties, and very little has been said about dynamic effects. In some sense this is not surprising since all the terms in the Ising model Hamiltonian commute, and no thus time dependence would be expected. However, inasmuch as the Ising model aims to approximate the behavior of real physical systems, and these are not always in equilibrium, the dynamics are of fundamental interest.

In practical terms, dynamic effects can manifest themselves when measurements are made with a.c. techniques, which are generally more convenient than static measurements. Sometimes it is observed that the frequency used to make measurements affects the results, and this provides a clear indication that dynamic effects are important. In principle one might then try to extrapolate the results to "zero" frequency but this can result in misleading conclusions, since more than one process may be operating. Such a situation is illustrated by the results in Fig. 20 which shows a plot of the out-of-phase component c¢¢ as a function of the in-phase component c¢ of the susceptibility of DyES for various frequencies [75]. It is clear that the values of c¢ extrapolated to c¢¢ = 0 are very different from the measured d.c. value, c_d.c. Evidence for a second relaxation process at even lower frequencies is provided by the points marked '5', corresponding to measurements at 5 Hz.

Figure 20.
A plot ot the out-of-phase susceptibility c¢¢ as a function of the in-phase c¢ for DyES for various frequencies at four different temperatures. The frequency of measurement, in Hz, is written beside each symbol. The curves are circles which pass through the origin and best fit the data. The extrapolated values of c¢ for c¢¢ = 0 are clearly different from the measured d.c. value, c_d.c.. After Ref. 75.

Dynamic effects are clearly important are cases in which the sample breaks into domains which must grow and shrink in response to an applied field. Such situations include ferromagnets below the Curie temperature, and also antiferromagnets undergoing first order phase transitions.

Observations of dynamic effects involving domain motion were, in fact, made [75] on the very first Ising-like ferromagnet studied, DyES, and possible mechanisms were discussed by Richards [76]. However, this material has an inconveniently low Curie temperature ( ~ 0.1 K), and more detailed experiments were later made by Kötzler and his associates on LiTbF₄, and on GdCI₃ whose Curie points are at 2.9K and 2.2K respectively. A number of interesting relaxation effects associated with domain wall motion were found over a wide of frequencies,[77-82] but so far there are no detailed microscopic theories to describe the results.

The other situation in which dynamic effects can be observed is the response to an a.c. field when the system is in a homogeneous phase. The effects that can be observed are not small, and in Fig. 21 we show results for one relaxation process as a function of magnetic field for DyAG at temperatures well below the Néel point [83]. Here both the d.c. and the a.c. measuring fields were applied along a [110] direction, for which no coupling to the antifferromagnetic order parameter would be expected.

Figure 21.
Field and temperature dependence of one of the relaxation times, IHF, of DyAlG. The arrow indicates the location of the phase boundary H_c at 1.8 K; at the other temperatures shown H_c is not very different. All the results therefore correspond to measurements in the antiferromagnetic phase. The broken line at 10^-5 indicates the lower limit of the measurements. After Ref. 83.

It can be seen that there are changes in the relaxation time of more than two orders of magnitude for applied fields as small as 0.1T, much weaker than the field 0.6T required to induce a transition from the antiferromagnetic to the paramagnetic phase. No explanation for these and similar phenomena has been found [83].

To account for dynamic effects in detail, there are two problems confronting the theory. One is to identify the non-Ising mechanisms, and their strengths, responsible for relaxation effects in the first place. The second is to calculate their observable effects in terms of the microscopic interactions. These are not easy problems to tackle,[76-84] and it would seem clear that dynamic effects in Ising-like systems will continue to provide a challenge to both theory and experiment for some time.

IV Conclusions

The work on Ising-like magnetic materials over the past 40 years has led to several conclusions. First, it has shown that the theoretical predictions of the standard near neighbor Ising model are generally confirmed, both with respect to thermodynamic properties over a wide range of temperatures, and the asymptotic behavior near critical points The experiments are not always easy to analyze unambiguously, but a healthy iterative process - theory guiding experiment, and experiment looking for appropriate tests of the theory - has been very successful.

Other conclusions relate to situations in which the experiments gave results that, at first, appeared to be in conflict with the theory. Closer inspection then revealed that there were features in the real material that were not included in the usual kind of Ising model. These have included competing near neighbor interactions, long range magnetic dipole interactions, and lattice structures that lead to new physical effects, such as first order transitions, coupling to antiferromagnetic order by an applied magnetic field, and suppression of order by frustration. So far some of these unusual Ising models have been studied only with a limited range of techniques, and further work in these areas would clearly be of interest.

Another area that has received relatively scant attention concerns dynamic effects Any such effects must, of necessity, involve interactions that are not completely Ising like, since simple Ising models have no time dependence. However, in real Ising-like materials time dependent effects are observed, and further study of these will be of interest.

The principal conclusion from all the past work in this field may be the fact that the Ising model has provided an unusually rich opportunity for both theory and experiment to interact, to the mutual benefit of both. There seems no reason why such interaction should not continue to flourish in this field.

This paper is dedicated to Ernst Ising and the field he created, and to the many theorists and experimentalist who have built on his very simple original ideas. I would also like to thank M. E. Fisher and M. Blume who have led me through much of the theory, and to my students and colleagues who, over the years, have unraveled many of the properties of Ising-like materials, expected and unexpected.

References

[1] See, for example, A. Abragam and B. Bleaney, in Electron Paramagnetic Resonance in Transition Metal Ions (Oxford University Press, New York, 1970).

[2] See, for example, W.P. Wolf, J. Phys. (Paris) C-1, 26 (1971), and reterences therein.

[3] A.H. Cooke, D.T. Edmonds, C.B.P. Finn and W.P Wolf, Proc. Phys. Soc., London 74, 791 (1959).

[4] R.J. Elliott and K.W.H. Stevens, Proc. Roy. Soc., London Ser. A219, 387 (1953).

[5] W.J. de Haas, J. van den Handel and C.J. Gorter, Phys. Rev. 43, 81 (1933); W.J. de Haas, J. van den Handel, C.J. Gorter, J. Becquerel, W.J. de Haas and J. van den Handel, Physica 3, 1133 (1936).

[6] L.J. de Jongh and A.R. Miedema, Adv. Phys. 23, 1 (1973).

[7] E. Stryjewski and N. Giordano, Adv. Phys 26, 487 (1977).

[8] B. Schneider, D.P. Landau, B.E. Keen and W.P. Wolf, Phys. Lett. 23, 210 (1966).

[9] J.H. Van Vleck, J. Chem. Phys. 5, 320 (1937).

[10] J.M. Daniels, Proc. Phys. Soc., London, Sec. A 66, 673 (1953).

[11] A H. Cooke, D.T Edmonds, F.R. McKim and W P Wolf, Proc. Soy. Soc., London, Ser. A 252, 246 (1959); A.H. Cooke et al., Proc. VII Int. Conf. Low Temp. Phys., 187, (1960)

[12] R. Frowein and J. Kotzler, Z. Phys. B 25, 279 (1976); R. Frowein and J. Kotzler, Phys. Rev. B 25, 3292 (1982).

[13] A.H. Cooke, D.T. Edmonds, C.B.P. Finn and W.P. Wolf, Proc. Roy. Soc. (London) Ser. A 306, 313 (1968).

[14] C. Domb, Adv. Phys, 9, 149 (1960).

[15] M. E. Fisher, Rep. Prog. Phys. 30, 615 (1967).

[16] G.T. Rado, Solid State Commun. 8, 1349 (1969); 9, vii(E) (1971).

[17] J.C. Wright et al., Phys. Rev. B 3, 843 (1971).

[18] I.R. Jahn, J. Ferré, M. Régis and Y. Farge, Solid State Commun. 28, 421 (1978).

[19] J. Hoffmann, Phys. Status Solidi B165, 517 (1991).

[20] See, for example, A. Abragam and B. Bleaney, in Electron Paramagnetic Resonance of Transition Ions (Oxford University Press, New York, 1970).

[21] D.J. Breed, K. Gilijamse and A.R. Miedema, Physica, 45, 205 (1969).

[22] P. Nordblad, D.P. Belanger, A.R. King, V. Jaccarino and H. Ikeda., Phys. Rev. B 28. 278 (1983).

[23] M.T. Hutchings, H. Ikeda and E. Janke, Phys. Rev. Lett. 49, 386 (1982).

[24] M. Ball, M.J.M. Leask, W.P. Wolf and A.F.G. Wyatt, J. Appl. Phys. 34, 1104 (1963)

[25] B.E. Keen, D.P. Landau and W P. Wolf, J. Appl. Phys. 38, 967 (1967).

[26] D.P. Landau, B.E. Keen, B. Schneider and W.P. Wolf, Phys. Rev. B 3, 2310 (1971).

[27] D.S. Gaunt and C. Domb, J. Phys. C1, 1038 (1968).

[28] W.P. Wolf, B. Schneider, D.P. Landau and B.E. Keen, Phvs. Rev. B 5, 4472 (1972).

[29] A.J. Guttmann, J. Phys. C 8, 4037 (1975).

[30] J.E. Rives and D.P. Landau, Phys. Rev. B 17, 4426 (1978).

[31] A.H. Cooke, D.A. Jones, J.F.A. Silva and M.R. Wells, J. Phys. C 8, 4083 (1975).

[32] W. P. Wolf and A.F.G. Wyatt, Phys. Rev.13, 368 (1964).

[33] C. Kittel, Phys. Rev. 82, 965 (1951).

[34] J. Als-Nielsen, L.M. Holmes and H.J. Guggenheim, Phys. Rev. Lett.32, 610 (1974).

[35] L.M. Holmes, J. Als-Nielsen and H.J. Guggenheim, Phys. Rev. B12, 180 (1975).

[36] A.L. Larkin and D.E. Khmel'nitskii, Zh. Eks Teor. Fiz. 56, 2087 (1969) [Sov. Phys. JETP 29, 1123 (1969)].

[37] A. Aharony, Phys. Rev. B 8, 3363 (1973); F. Wegner and E. Riedel, ibid. 7, 248 (1973).

[38] N. J. Als-Nielsen, L.M. Holmes and H.J. Guggenheim, Phys. Rev. Lett. 32, 610 (1974).

[39] L.M. Holmes, H.J. Guggenheim and J.P. Maita, Phys. Lett. A 50, 163 (1974).

[40] G. Ahlers, A. Kornblit and H.J. Guggenheim, Phys. Rev. Lett.34, 1227 (1975).

[41] J. Als-Nielsen, Phys. Rev. Lett. 37, 1161 (1976).

[42] R. Frowein and J. Kotzler, Z. Phys. B 25, 279 (1976).

[43] J.A. Griffin, J.D. Litster and A. Linz, Phys Rev. Lett. 38, 251 (1977); J.A. Griffin and J.D. Litster Phys. Rev. B 19, 3676 (1979).

[44] O.G. Mouritsen and S.J. Knak Jensen, Phys. Rev. B 19, 3663 (1979).

[45] R. Frowein, J. Kdtzler and W. Assmus, Phys. Rev. Lett. 42, 739 (1979).

[46] P. Bcauvillain, C. Chappert and I. Laursen, J. Phys. C 13, 1481 (1980).

[47] R. Frowein, J. Kotzler. Phys. Rev. B 25, 3292 (1982); R. Frowein, J. Kotzler, B. Schaub and H.G. Schuster, ibid 4905 (1982).

[48] M.E. Fisher, Proc. Roy. Soc. London Ser A 254, 66 (1960).

[49] M. Ball, W.P. Wolf and A.F.G. Wyatt, Phys. Lett. 10, 7 (1964).

[50] A.F.G. Wyatt, J. Phys. C 1, 684 (1968).

[51] J.F. Dillon, Jr., E. Yi Chen, N. Giordano and W.P. Wolf, Phys. Rev. Lett. 33, 98 (1974).

[52] See, for example, K. Motizuki, J. Phys. Soc. Japan 14, 759 (1959), and references contained therein.

[53] M. Blume, L.M. Corliss, J.M. Hastings and E. Schiller, Phys. Rev. Lett. 32, 544 (1974).

[54] R. Alben, M. Blume, L.M. Corliss and J.M. Hastings, Phys. Rev. B 11, 295 (1975).

[55] N. Giordano and W.P. Wolf, Phys. Rev. B 21, 2008 (1980), W.P. Wolf, Physica A 177, 253 (1991).

[56] E. Yi Chen, J.F. Dillon Jr., E.l. Blount and L.G. Van Uitert, J. Appl. Phys. 50, 1841 (1979).

[57] J.F. Dillon Jr., E.l. Blount, E. Yi Chen, E.M. Gyorgy and L.G. Van Uitert, J. Appl. Phys. 50, 1844 (1979).

[58] J.F. Dillon Jr., E.M. Gyorgy, E.l. Blount, E. Yi Chen and L.G. Van Uitert, J. Appl. Phys. 49, 1371 (1978).

[59] J.F. Gregg, L.D. Morris, M.R. Wells and W.P. Wolf, J. Phys. (Paris) 49, C-8 2027 (1988).

[60] J.F. Gregg et al., J. Appl. Phys. 67, 5430 (1990).

[61] S.J. Dawson, et al., J. Magn. Magn. Mater. 90& 91, 184 (1990); ibid., 104-107 (1992).

[62] W.P. Wolf, in Multicritical Phenomena, edited by R. Pynn and A. Skjeltorp (Plenum Publishing Cor , 1984), 13.

[63] N. Giordano and W.P. Wolf, Phys. Rev. Lett. 39, 342 (1977)

[64] C.A. Ramos, A.R. King and V. Jaccarino, Phys. Rev. B 40, 7124 (1989).

[65] M.J. Harris et al., Phys. Rev. Lett. 79, 2554 (1997).

[66] R. Moessner, Phys. Rev. B 57, R5587 (1998).

[67] S.T. Bramwell and M.J. Harris, J. Phys. Condes. Matter 10, L215 (1998).

[68] L. Pauling, The Nature of the Chemical Bond (Cornell, Ithaca, NY, 1960), 3rd. ed., 465-468.

[69] R. Siddharthan et al., Phys. Rev. Lett. 83, 1854 (1999).

[70] B.C. den Hertog and M.J.P. Gingras, Phys. Rev. Lett. 84, 3430 (2000).

[71] A.P. Ramirez et al., Nature (London) 399, 333 (1999).

[72] H.W.J. Blote, R.F. Wielinga and W.J. Huiskamp, Physica 43, 549 (1969).

[73] M.J. Harris, S.T. Bramwell, P.C.W. Holdsworth and J.D.M. Champion, Phys. Rev. Lett. 81, 4496 (1998).

[74] B.E. Keen, D.P. Landau and W.P. Wolf, Phys. Lett. 23, 202 (1966).

[75] A.H. Cooke, D.T. Edmonds, C.B.P. Finn and W.P. Wolf, Proc. Roy. Soc. (London) Ser. A 306, 335 (1968).

[76] P.M. Richards, Phys. Rev. 187, 690 (1969).

[77] J. Kotzler, M. Grahl, I. Sessler and J. Ferré, Phys. Rev. Lett. 64, 2446 (1990).

[78] M. Grahl et al., J. Appl. Phys. 69, 6179 (1991).

[79] M. Grahl and J. Kotzler, J. Magn. Magn Mater. 104, 219 (1992).

[80] J. Kotzler et al., Phys. Rev. Lett. 71, 177 (1996).

[81] C. Marx, D. Gorlitz and J. Kotzler, Phys. Lett A 210, 141 (1996).

[82] M. Grahl and J. Kotzler, J. Phys. (Paris) 49, C8-915 (1988); M. Grahl, and J. Kotzler, Z. Phys. B 75, 527 (1989).

[83] M. Ritter and W.P. Wolf, J. Magn. Magn. Mater. 54-57, 1329 (1986); M. Ritter, thesis (Yale University, 1986) (un-published).

[84] E. Frey, F. Schwabl and S. Thoma, Phys. Rev. B 40, 7199 (1989).

Figure 5. Spontaneous sublattice magnetization as a function of temperature for DyPO₄. The points (o) represent experimental results of magneto-electric measurements; the two solid lines represent the results of a calculation based on a low- temperature series expansion with one adjustable constant, and a fit to a power-law with a fitted critical exponent b = 0.314. The broken line represents the molecular field theory. After Ref. 16.

Publication Dates

• Publication in this collection
  09 Jan 2002
• Date of issue
  Dec 2000

History

• Received
  03 Aug 2000