Abstract
A new discrete distribution is introduced. The distribution involves the negative binomial and size biased negative binomial distributions as sub-models among others and it is a weighted version of the two parameter discrete Lindley distribution. The distribution has various interesting properties, such as bathtub shape hazard function along with increasing/decreasing hazard rate, positive skewness, symmetric behavior, and over- and under-dispersion. Moreover, it is self decomposable and infinitely divisible, which makes the proposed distribution well suited for count data modeling. Other properties are investigated, including probability generating function, ordinary moments, factorial moments, negative moments and characterization. Estimation of the model parameters is investigated by the methods of moments and maximum likelihood, and a performance of the estimators is assessed by a simulation study. The credibility of the proposed distribution over the negative binomial, Poisson and generalized Poisson distributions is discussed based on some test statistics and four real data sets.
Key words
characterization; discrete distributions; Estimation; Vuong test statistic; mixture distributions; thunderstorms data
INTRODUCTION
In observational studies it is observed that due to lack of well defined sampling frames for plant, human, insect, wildlife and fish populations, the scientists/ researchers cannot select sampling units with equal probability. As a result the recorded observations on individuals in these populations are biased unless every observation is given an equal chance of being recorded. As such biased data arise in all disciplines of science, so statisticians and researchers have done their best to find out solutions for correction of the biases. In this regard, the weighted distribution theory gives a unified approach for modeling biased data, Fisher (1934)FISHER RA. 1934. The effects of methods of ascertainment upon the estimation of frequencies. Ann Eugenic 6: 13-25., later on Rao (1985)RAO CR. 1985. Weighted distributions arising out of methods of ascertainment. In Atkinson AC AND Fienberg SE (Eds.), A Celebration of Statistics Chapter 24. pp. 543-569. New York: Springer-Verlag. and Patil (1991)PATIL GP. 1991. Encountered data, statistical ecology, environmental statistics, and weighted distribution methods. Environmetrics 2: 377-423. studied it in a unified manner. Those pioneers have pointed out the situations in which the recorded observations cannot be considered as a random sample from the original distribution like non-experimental, non-replicated and non-random categories. This may be due to one or more reasons, such as non-observability of some events, damage caused to original observations and adoption of unequal probability sampling (see Jain et al. 2014JAIN K, SINGLA N AND GUPTA RD. 2014. A weighted version of gamma distribution. Discus Math Prob Stat 34: 89-111.). Patil and Rao (1977)PATIL GP AND RAO CR. 1977. Weighted distributions: a survey of their application. In Krishnaiah PR (Ed.), Applications of Statistics, pp. 383-405. North Holland Publishing Company. stated that " Although the situations that involve weighted distributions seem to occur frequently in various fields, the underlying concept of weighted distributions as a major stochastic concept does not seem to have been widely recognized", the same quote is applicable today but, unfortunately a rare work is seen on this topic.
In order to remove the biases and to obtain the suitable distribution, the researchers usually adopt the approach of weighted concept of biased observation which leads towards the development of a weighted distribution. For a non-negative integer valued random variable X, its probability mass function can be defined as where θ is a vector parameter, and let ω(k) be a non negative function on which does not need to be zero or one and may exceed unity but it should have a finite expectation, i.e., . Suppose that when the event occurs, the weight is used to adjust the probability. Therefore, the record k is thus the realization of count random variable Y which is a weighted version of X and its probability mass function (pmf) is given by
where can depend on a parameter ψ representing the recording mechanism, and it may also be connected to the underlying initial vector parameter θ. A detailed account of weight functions is available in Patil and Rao (1986)PATILL GP, RAO CR AND RATNAPARKHI M. 1986. On discrete weighted distribution and their use in model choice for observed data. Commun Statisit Theory Math 15: 907-918.. Some particular cases of the weight functions are the standard distributions with Constant, , the size-biased distributions with weight , the popular COM-Poisson with weight (see Balakrishnan 2014BALAKRISHNAN N. 2014. Methods and Applications of Statistics in Clinical Trials: Planning, Analysis and Inferential Methods. J Wiley & Sons, Inc., pp. 511-512), Neel and Schull (1966)NEEL JV AND SCHULL WJ. 1966. Human Heredity. Chicago: University of Chicago Press. proposed the weighted Poisson distribution with a weight as Poisson distribution, i.e., and binomial distribution with weight function (see Kokonendji and Casany 2012KOKONENDJI CC AND CASANY MP. 2012. A note on weighted count distributions. J Stat Theory Appl 11: 337-352.).
In this paper, we construct a weighted version of the two parameter discrete Lindley distribution introduced by Hussain et al. (2016)HUSSAIN T, ASLAM M AND AHMAD M. 2016. A two parameter discrete Lindley distribution. Rev Colomb Estad 39: 45-61. by making use of the weight function . Construction and motivations of the introduced distribution are outlined in the section below. Rest of the paper is organized as follows. The section ’Statistical Properties Of The WNBL Distribution’ gives several properties of the proposed distribution, such as probability generating function, moments, factorial moments, recurrence relation between moments and negative moments. In the section ’Parameter Estimation and Inference’, the estimation of the model parameters is investigated by the methods of moments and maximum likelihood, and performance of the estimators is assessed by a simulation study. A characterization for the distribution via the probability generating function is investigated with a discussion to self decomposability and infinite divisibility. Credibility of the proposed distribution over the negative binomial, Poisson and generalized Poisson distributions is also discussed based on some evaluation statistics and four real data sets. The last section gives the drawn conclusion.
THE PROPOSED DISTRIBUTION WITH MOTIVATIONS
Hussain et al. (2016) developed the two parameter discrete Lindley distribution with the pmf
and
Considering the weight function and substituting it along with equation (2) into equation (1), we get
and .
Hereafter, the weighted version of the two parameter discrete Lindley distribution shall be denoted by the weighted negative binomial Lindley (WNBL) distribution. Now, we give some motivations for the proposed distribution.
Motivation 1. The pmf of the negative binomial (NB) distribution is given as
and
or equivalently
where k denotes the number of failures/success before the failure/success, p is the probability of success and C is the normalization constant which equals . In the NB distribution, we repeat the number of Bernoulli trials in order to obtain a fixed number of successes, while if the number of failures/successes increases linearly on each trial then the probability of exactly k failures/successes can be expressed as where which is the pmf of the WNBL distribution.
Moreover, it can be noted that the probability function given by (2) is a generalized form of the NB with vector parameter and also the discrete Lindley with vector parameter
Motivation 2.
The binomial coefficient in the equation (3) represents the number of ways in which the fixed number of failures/successes are obtained when these failures/successes increase linearly on each trial.
Motivation 3.
It is also worth mentioning that the model given in equation (3) is recognized as a mixture of the NB distribution and the size biased negative binomial distribution (SBNB), that is,
Motivation 4.
The model given by (3) can describe the thunderstorm activities as shall be outlined in the application section using two real data sets from such area. Thunderstorms activities often affect the planning of space missions and launch operations at different launching stations because of unstable meteorological norms associated with them. For this purpose several statistical distributions are used to represent the variation of the thunderstorms activities and search out that negative binomial and its modified forms are usually preferred for such activities (see Sakamoto 1973SAKAMOTO CM. 1973. Application of the Poisson and negative binomial models to thunderstorm and hail days probabilities in Nevada. Monthly Weather Review 101: 350-355.). Therefore, we model such activities by introducing a weighted and mixed version of the negative binomial and Lindley distributions. The weighted distributions are important for the adjustment of probability of occurrences and removal of biasedness from the data, while the mixed distributions are usually used in heterogeneous and over-dispersed data sets. The proposed model not only overcomes the heterogeneity issue but also handles the over-dispersion because of its mixture representation which makes it better than the negative binomial, Poisson and generalized Poisson distributions.
Further motivations for the WNBL distribution are given in the next notes.
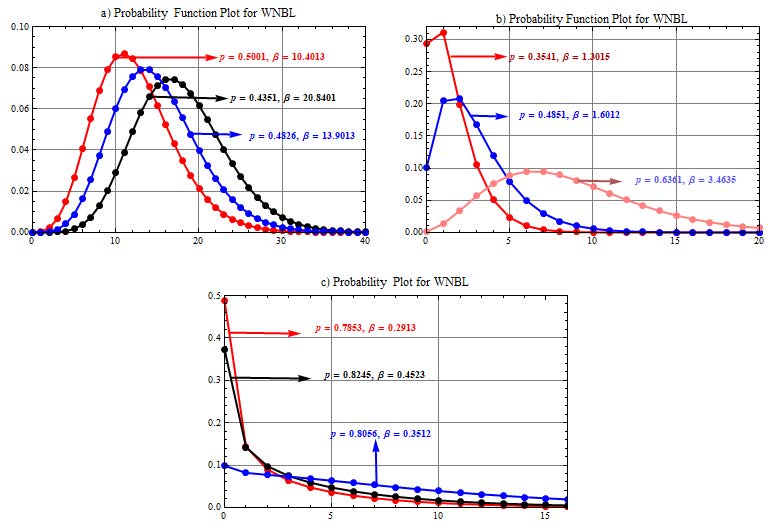
Figure 1 portrays that the WNBL distribution shows symmetrical behavior when p < 0.20 and β increases. Whereas, for smaller β and higher p, the distribution becomes positively skewed. The distribution also exhibits bimodal and reverse J shapes.
Now, we give two prime measures of the distribution.
The survival and hazard rate functions of the WNBL distribution are
and
respectively. Where
and , are the hypergeometric series function and the Pochhammer’s symbol, respectively, the series converges for and .
Clearly
therefore, the hazard rate function of the WNBL distribution is bounded above, which is an important property for the lifetime models.
Figure 2 displays increasing, decreasing and bathtub shape (BTS) hazard functions. It is observed that the traditional statistical distributions, such as the Poisson, generalized Poisson and NB distributions, cannot be used efficiently in models of count data with many zeros. The Poisson distribution tends to under-estimate the number of zeros, while the NB may over-estimate zeros (see Saengthong and Bodhisuwan 2013SAENGTHONG P AND BODHISUWAN W. 2013. Negative binomial-crack (NB-CR) distribution. Int J Pure Appl Math 84: 213-230.). Although the traditional count models have generally increasing or decreasing failure rates yet unable to exhibit BTS hazard rates.
In view of the discussion above, some other motivational factors of the proposed model shall be outlined later and they are: i) Possessing BTS hazard function along with increasing/decreasing hazard rate characteristics which are seldom observed in discrete distributions. ii) Possessing bounded hazard function iii) Being an over- and under-dispersed statistical model. iv) Being a self decomposable and infinitely divisible model. v) Being a characterizable function which is a milestone in model selection.
STATISTICAL PROPERTIES OF THE WNBL DISTRIBUTION
The recognition of any discrete probability distribution is usually based on its probability generating function (pgf). The following theorem gives the pgf of the WNBL distribution.
Proposittion1: If WNBL then the pgf of the random variable Y is expressed as
where and
Proof: The pgf from the definition is expressed as . Using equation (3), we have
which by simplification, equation (6) is obtained, which completes the proof.
Corollary 1: In equation (6), if t is replaced by et, we get the moment generating function (mgf) of the WNBL distribution as
where .
The rth derivatives of equation (7) with respect to t at t = 0 yield the moments. In particular, for r = 1 we have
for r = 2 we have
for r = 3 we have
and for r = 4 we have
Moreover, by definition, the rth non central moment can be expressed as
Differentiating the equation above with respect to p we get
which by simplification yields the recurrence relation
.
Similarly, by definition, the rth central moment can be expressed as
Differentiating the above equation with respect to p and simplifying it, we get
.
OVER-AND UNDER-DISPERSION
In statistics, the phenomenon of over- and under-dispersion relative to the Poisson distribution is generally observed in count data and well known in statistical literature. There are various causes of such phenomenon, like heterogeneity and aggregation for over-dispersion and repulsion for under-dispersion although less frequent (see Kokonendji and Mizre 2005KOKONENDJI CC AND MIZRE D. 2005. Overdispersion and Underdispersion Characterization of Weighted Poisson Distribution (Technical Report No. 0523) France LMA. Technical report.). In order to see the reflection of over- and under-dispersion pattern, the researchers usually take the support of the index of dispersion (ID) which is defined as variance-to-mean ratio, which indicates the suitability of distribution in, under- or over-dispersed data sets. If the distribution is over-dispersed (under-dispersed). The index of dispersion for the WNBL distribution is
For indicating the dispersion pattern we first consider that β < 1 which implies that . If and then ID can be re expressed as
since C > D then 1- pC < 1-pD or . Therefore, the WNBL is an over-dispersed model for all values of p. However, if β >1 this implies that . Let and then ID can be rewritten as
As it is evident that L > S, then or . Hence, ID< 1 if and .
OTHER MOMENTS MEASURES
The following theorems gives factorial moments and negative moments.
Theorem 1: If WNBL, then the rth descending factorial moment of Y is given by
where and .
Proof: The rth descending factorial moment for Y can be defined as . Using the expression , we have
By using the binomial series , we obtain
hence, we get
After some algebraic manipulation, the equation (8) is attained and it generates a recursive relation between r and (r - 1) descending factorial moments as
where which completes the proof.
Theorem 2: If WNBL , the rth ascending factorial moment of Y is given by
where .
Proof: The rth ascending factorial moment is defined as , this implies that
By using the hypergeometric series function , we get the equation (10), where
and
Thus the theorem is proved.
As it is known, the ordinary moments are generally helpful in estimating the unknown parameters. However, due to recent developments in inverse theory of the random variables, the negative moments are gaining momentum in life testing phenomena, estimation purposes and identifying the models. The negative moments are being used in irreversible damage to manufacturing materials due to damage process such as creep, corrosion, creep fracture, wear, shrinkage, aging and cracking (see Ahmad 2007AHMAD M. 2007. On the theory of inversion. Int J Stat Sci 6: 43-53.). Therefore, the next theorem deals with the negative moments of the WNBL distribution.
Theorem 3: If WNBL the first order negative moment of Y is given by
where and .
Proof: By definition, , we have
By simplification, we get the equation (11) where
and
This completes the proof.
Corollary 2: The rth order negative moment of WNBL can be expressed as
where
the series converges for and .
PARAMETER ESTIMATION AND INFERENCE
In this section, estimation of parameters of the distribution is investigated by the methods of moments (MM) and maximum likelihood (ML), and a performance of the estimators is assessed by a simulation study.
MOMENTS METHOD
Let be a random sample drawn from the WNBL distribution with the observed values . Equating the first two sample moments, and with their associated population moments
and
then the MM estimators of the WNBL are obtained.
Alternatively, the MM estimators can also be obtained using the suggested approach by Khan et al. (1989)KHAN AMS, KHALIQUE A AND ABOUAMMOTH AM. 1989. On estimating parameters in a discrete Weibull distribution. IEEE T Reliab 38: 348-350. via minimizing the expression
with respect to p and β. Hence,
yields two equations which are not in closed form, so parameters are estimated using numerical optimization techniques via Mathematica 8 computational packages.
MAXIMUM LIKELIHOOD METHOD
If is a random sample drawn from the WNBL distribution with the observed values then we get the log-likelihood function
By partially differentiating both sides of the equation above with respect to p and β and equating them to zero, we get the MLEs of pand β respectively, as
and
Similarly, the second derivatives of the equation (12)) and equation (13) with respect to p and β, respectively, are
and
Also, the second derivative of equation (12) with respect to β or equation (13) with respect to p yields
where is the logarithmic derivative of the gamma function. The MLEs are computed using computational packages, such as Mathematica 7. In view of the regularity conditions (see Rohatgi and Saleh 2002ROHATGI VK AND SALEH AKE. 2002. An Introduction to probability and Statistics. Singapore: John Wiley and Sons (Asia) Pte Ltd., pp. 419), we observed that the MLEs of WNBL parameters satisfy such conditions, where i) The parameters are subset of the real line, ii) exist for all values of p and β, iii) iv) for all values of p and β.
Moreover, the MLEs and of the WNBL distribution have an asymptotic bivariate normal distribution with vector mean (p,β) and variance-covariance matrix (I(p,β))-1, where I(p,β) denotes the information matrix given by
,
where
The expectations above can be obtained numerically.
SIMULATION SCHEME
As it is mentioned in the introduction that the WNBL(p,β) distribution can be viewed as a mixture of the negative binomial, NB(p,β), and size biased negative binomial, SBNB(p,β), distributions. So, in order to generate random data ki, i=1,2,...n, from the WNBL we used the following algorithm.
Algorithm: i) Generate Ui,i = 1,2,...,n,from the uniform distribution on the interval (o,1). ii) Generate NBi,i=1,2,...,n from the negative binomial distribution NB(p,β) with support k=0,1,.... iii)Set Y1=NBi. iv) Generate SBNBi,i=1,2,...,n, from the size biased negative binomial distribution SBNB(p,β) with support k=1,2,.... v) Set Y2=SBNBi. If , then set ki=Y1 otherwise set ki=Y2,i=1,2,...,n.
SIMULATION STUDY
In this section, we perform some numerical experiments to see how the estimates studied by using the above listed methods (MM and ML) as well as their asymptotic results for finite samples. All the numerical results are performed via Mathematica 8 using the random numbers generator code. We consider the following different model parameters. Model-I: , Model-II: and Model-III: for both MMEs and MLEs. We consider the following sample sizes n=20(small), 50 (moderate), and 100,200,500 (large). For each set of the model parameters and for each sample size, we compute the MMEs and MLEs of each β and p. We repeat this process 1000 times and compute the average bias and mean square error (MSE) for all replications in the relevant sample sizes. The results are reported in Table I and III.
Discussion: Some notes are very clear from the simulation studies, such as the bias decreases as sample size increases for both MLEs and MMEs. Moreover, we conclude that the bias takes negative and positive signs, and it approaches to the value zero for both signs while the MSE decreases as the sample size increases.
CHARACTERIZATION
Characterization of probability functions is of importance to determine the exact probability distribution, which means that under certain conditions a family of distributions is the only one possessing a designated property which will resolve the problem of model identification. Therefore, the next theorem gives characterization of the WNBL distribution.
Theorem 4: If is the pgf of a certain distribution defined on the support with parameters , then
for with , holds if and only if Y has the WNBL distribution with pmf defined by equation (3).
Proof: If has the WNBL distribution given by (3), then the equation (14)) is satisfied.
On the other side, suppose the equation (9) holds, which yields descending factorial moments, hence for and we have
For r=2 and expressed in the above equation, we get
Also, for r=3 and expressed in the equation above, we obtain
and so on. Since, factorial moment generating function is defined as
by substituting and so on in equation (15) we get
Hence,
After some algebra, we get
Replacing by t we have
By calculating the xth derivative of Gt(t) at t=0,
yields equation (3). This completes the proof.
DISCRETE ANALOGUES OF SELF-DECOMPOSABILITY
Definition 5.1 (α-thinning) Let be a non-negative integer-valued random variable and let , then the α-thinning of X using the Steutel and van HarnSTEUTEL FW AND VAN HARN K. 1979. Discrete analogues of self-decomposability and stability. Ann Prob 7: 893-899. operator is defined by
where Zi(i=1,2,...,X) are mutually independent Bernoulli random variables with P(Zi=1)= α and P(Zi=0)=1-α. Additionally, the random variables Zi are independent of X. The pgf of the random variable is
Definition 5.2 (Discrete Infinite divisibility) Let X be a non-negative integer-valued random variable, then X is said to be infinitely-divisible, for every non negative integer n, if X can be represented as a sum of n independent and identically distributed (i.i.d.) non-negative random variables Xn;i(i=1,2,...,n), that is,
Note that the distributions of X and Xn;i do not necessarily have to be of the same family. Moreover, a random variable X is said to be discrete infinitely-divisible if the random variables Xn;i only take non-negative integer values. A necessary condition for such random variable X to be well defined is P(X=0)>0 (to exclude the trivial case we assume P(X=0)<1), see Steutel and van HarnSTEUTEL FW AND VAN HARN K. 1979. Discrete analogues of self-decomposability and stability. Ann Prob 7: 893-899.(1979).
Definition 5.3 (Discrete self-decomposability) A non-negative integer-valued random variable X is said to be discrete self-decomposable if for every the random variable X can be written as where the random variables and are independent, which in terms of the pgf can be expressed as
where is the pgf of . We have noted that the distribution of uniquely determines the distribution of X. Moreover, a discrete infinitely-divisible distribution is discrete self-decomposable.
By using the definitions above, the following propositions show that the WNBL distribution is a self decomposable and infinitely-divisible distribution.
Proposition 2: If X1,X2 and X3 are independent random variables such that Bernoulli, NB(p,β) and Geo(1-p), then Y = X1+ X2+ X3 has the WNBL(p,β) distribution.
Proof: Since Bernoulli, its mgf is expressed as . Similarly, X2 and X3 having the mgfs and respectively. Since Y = X1 + X2 + X3 hence the mgf of Y is
which is the mgf of the WNBL distribution. This completes the proof.
Proposition 3: If WNBL for , are independent random variables, then , and having the WNBL distribution.
Proof: As WNBL for , hence the mgf of is
which gives the required proof.
Note in the expression above
where Binomial() and NB(), which shows the discrete self-decomposability.
TEST STATISTICS WITH DATA APPLICATIONS
In this section, the credibility of the proposed model is checked via over- and under-dispersed count data sets. In this regard, for modeling over-dispersion phenomena, we have used three data sets: (i) The counts of European red mites on apple leaves, (ii) Accidents of 647 women working on H.E. shells during five weeks, (iii) The thunder storm activity at Cape Kennedy. While, for under-dispersion case the number of outbreaks of strikes in UK coal mining industries is used. All the data sets are modeled via the four probability models: WNBL, NB, Poisson (Poi) and Generalized Poisson (GP) distributions. Since NB distribution is the compounded mixture of gamma and Poisson distributions, so it is usually recommended for heterogeneity and over-dispersion, while the generalized Poisson distribution is a mixed and weighted version as well as a generalized form of Poisson distribution, therefore it is used to model over- and under-dispersed data sets. The probability functions of these models are given in the next table
For comparison purposes, we have used seven goodness-of-fit statistics. The computation of these statistics is based on the MLEs which are computed by using Mathematica 7 computational package. These statistics include Log-Likelihood (l), Akaike information criterion (AIC), Bayesian information criterion (BIC) and corrected Akaike information criterion (AICc), Kolmogrov Smirnov (KS) statistics and statistics with p-values. The formulae of such statistics are and , where m denotes the number of parameters, denotes the log-likelihood function evaluated at the MLEs, n denotes the number of observations in a sample,g denotes the number of classes and , and denote the observed frequencies, expected frequencies and cumulative distribution function of the class, respectively.
Vuong Test: The chi-square approximation to the distribution of the likelihood ratio test statistic is valid only for testing restrictions on the parameters of a statistical model, i.e., and are nested hypotheses. With non-nested models, we cannot make use of likelihood ratio tests for model comparison. In this case, information criteria, like AIC and BIC as well as the Vuong test for non-nested models are useful. Vuong (1989)VUONG QH. 1989. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 57: 307-333. proposed a likelihood ratio-based statistic for testing the null hypothesis that the competing models are equally close to the true data generating process against the alternative that one model is closer. Let us consider two statistical models based on the probability mass functions and posses equal number of parameters. Define the likelihood ratio statistic for the model against as
where and are the maximum likelihood estimators in each model based on n number of observations(see Denuit et al. 2007DENUIT M, MARCHAL X, PITREBOIS S AND WALHIN JF. 2007. Actuarial Modelling of Claim Counts Risk Classification Credibility and Bonus-Malus Systems. John Wiley.), denotes the observed frequency of the class and total number of classes . If both models are strictly non-nested then under we have the test statistics , where
In order to select an appropriate model, we usually construct the following hypothesis
against
i.e., the model A is defined to be better than model B if model A’s distance to the truth is smaller than that of model B, or That is, the model B is defined to be better than model A if model B’s distance to the truth is smaller than that of model A, where denotes the Kullback-Leibler distance measure, with corresponding critical values. The decision is as follows. i) Reject when in favor of A and Reject when in favor of B, where denotes the level of significance.
DESCRIPTION OF THE DATA SETS WITH THEIR FITTING
In biological research, researchers are often concerned with animals and plants counts for each of set of equal units space and time. Among these sets of counts, some counts may perhaps be well fitted by the Poisson distribution where the equi-dispersion phenomenon in the data is observed. But in discrete data sets the two other dispersion cases are also observed. The over-dispersion generally arises when the events or organisms are aggregated, clustered or clumped in time and space, while the under-dispersion is due to more regular positioning than that produced by a Poisson mechanism (see Ross and Preece 1985ROSS GJS AND PREECE DA. 1985. The negative binomial distribution. The Statistician 34: 323-336.). So, in the coming data applications we have also used the Vuong test for selecting a model which possesses the same number of parameters at significance level 0.08, for this purpose we have compared the proposed model with the NB and GP, not with the Poisson distribution because the latter one is unsuitable for over- and under-dispersed data.
The counts of European red mites on apple leaves(Data I):Garman (1951)GARMAN P. 1951. Original data on European red mite on apple leaves. Technical report. Report. Connecticut. of the Connecticut Agricultural Experiment Station selected 25 leaves at random from each of six McIntosh trees in a single orchard receiving the same spray treatment and the number of adult females counted on each leaf. These observations given in Table III of the Appendix and were first recorded by Bliss and Fisher (1953)BLISS CI AND FISHER RA. 1953. Fitting the negative binomial distribution to biological data. Biometrics 9(2): 176-200., and later on were mentioned by Jain and Consul (1971)JAIN GC AND CONSUL PC. 1971. A generalized negative binomial distribution. SIAM J Appl Math 21: 501-5013. The summary statistics of these observations is provided in Table Iv as given in Appendix which clearly indicates the over-dispersed nature of the data. In order to fit the competing models to this data set we have used the MLE estimates. The summary of test statistics is provided in Table V which depicts that the proposed model is the most suitable choice of such data with least loss of information. Moreover, the selection of a suitable non-nested model is also checked via Vuong test. The Vuong test statistics values along with p-value for comparison between WNBL-GP and WNBL-NB are given as i)Z=-1.7548, p-value=0.0793 and ii)Z=-1.7512, p-value=0.0799 which clearly indicates the suitability of the proposed model by showing minimum p-value.
Accidents to 647 women working on H. E. shells during five weeks(Data II): Miss Broughton, Head Welfare Officer, and the various Welfare Supervisors were the first to provide this numerical data set to Industrial Fatigue Research Board in 1919 (see Greenwood and Woods, 1919GREENWOOD M AND WOODS HM. 1919. The Incidence of Industrial Accidents upon Individuals with Special Reference to Multiple Accidents. Industrials Fatigue Research Board Report URL https://ia802705.us.archive.org/29/items/ncidenceofindus00grea/incidenceofindus00grea.pdf. Online Address.
https://ia802705.us.archive.org/29/items...
). Later on Greenwood and Yule (1920)GREENWOOD M AND YULE GU. 1920. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. J Roy Stat Soc 83: 255-279. and Jain and Consul (1971) used it for analysis purpose. This data set is displayed at Table VI and its descriptive statistics are provided in Table VII which shows an over-dispersed behavior. The earlier mentioned test statistics indicate that the proposed model is the most suitable one according to all mentioned statistics with least loss of information behavior and the results are displayed in Table VIII as given in the Appendix. Furthermore, the Vuong test statistics values along with p-value for comparison between WNBL-GP and WNBL-NB are given as i)Z=11.4348,p-value=0.0001 and ii) Z=18.08284,p-value=0.0001 which clearly indicates that the proposed model is better than the competing models.
Number of outbreaks of strikes in UK coal mining industries in four successive week periods during 1948-1959(Data III): This data set is given by Table IX and was analyzed by Castillo and Perez-Casany (1998)CASTILLO I AND PEREZ-CASANY M. 1998. Weighted Poisson distributions for overdispersion and underdispersion situations. Ann Inst Statist Math 50: 567-585., noting that they reported it from Kendall (1961)KENDALL MG. 1961. Natural law in social sciences. J R Stat Soc Ser A 124: 1-19.. Later on a number of authors, like Ridout and Besbeas (2004)RIDOUT MS AND BESBEAS P. 2004. An empirical model for under dispersed count data. Statist Model 4: 77-89., Chakraborty and Chakravarty (2012)CHAKRABORTY S AND CHAKRAVARTY D. 2012. Discrete gamma distributions: Properties and parameter estimations. Commun Statist Theor Meth 41: 3301-3324. and Alamatsaz and Dey (2016)ALAMATSAZ MH AND DEY S. 2016. Discrete generalized Rayleigh distribution. Pak J Stat 32(1): 1-20., studied it. Table X as given in the Appendix displays the descriptive statistics of this data set and indicates that it is under-dispersed. Further, comparison among the competing distributions is provided in Table XI which indicates that the proposed model is also an ideal model for under-dispersed data by showing not only the least Chi-Square test statistics but also minimum AIC, BIC and AICc, thus depicting that the model is the least loss of information model for under-dispersed data set too. Also, Vuong test statistics with p-values for comparison between WNBL-GP and WNBL-NB are listed as i)𝐙 = 1.8540, p-value=0.0673 and ii)𝐙=4.4281, p-value=0.0001 which again indicates the suitability of the proposed model.
Thunderstorm Activity at Cape Kennedy(Data IV): One of the major problem that the meteorologists usually faced is the forecasting of afternoon convective thunderstorm activity at the Cape Kennedy Florida. Usually thunderstorms are of primary concern in the design of launch vehicles, in the planning of space missions, and in launch operations at Cape Kennedy because of high winds, lightning hazard, and extreme turbulence associated with this atmospheric phenomenon. In thunderstorm activity, the occurrence of successive thunderstorm events (THEs) is often dependent process meaning that the occurrence of THEs indicates that the atmosphere is unstable and the environmental conditions are favorable for the formation of further thunderstorm activity. For more details on THEs, see Falls et al. (1971)FALLS L, WILLIFORD WO AND CARTER MC. 1971. Probability distributions for thunderstorm activity at Cape Kennedy, Florida. J Appl Meteorol 10: 97-104.. Data set of thunderstorm activity at Cape Kennedy is displayed in Table XII at the Appendix. As for thunderstorm activities the Poisson distribution is not a proper choice, hence the proposed model is compared with the NB and GP distributions based on the expected frequencies, , AIC, and p-values. The expected frequencies along with the test statistics of this data set are provided in the Tables XIII, XIV and XV. Vuong test statistics with p-values are displayed in Table XVI and Table XVII as given in Appendix, which clearly indicate the supremacy behavior of the proposed model over the competing distributions, except in February GP is recommended.
CONCLUSIONS
A new discrete model, named weighted negative binomial Lindley distribution, is proposed and its various properties are obtained involving generating functions, moments, recurrence relations between moments, random number generation, characterization, self-decomposability and infinite divisibility. Further, some applications of the model are studied. It is found that model is not only mathematically amenable but also recommended for many types of over- and under-dispersed count data sets. Moreover, the proposed model is also recommended for modeling the thunderstorms data and may help the scientists for proper planning of space missions and in launch operations at different stations in the presence of thunderstorms activities.
ACKNOWLEGMENTS
The author express his thanks to Associate Editor of the mathematical sciences area and the two referees for careful reading of the paper and providing valuable comments. Special thanks to Professor Tassaddaq Kiani for his sincere help during the progress of this paper.
REFERENCES
- AHMAD M. 2007. On the theory of inversion. Int J Stat Sci 6: 43-53.
- ALAMATSAZ MH AND DEY S. 2016. Discrete generalized Rayleigh distribution. Pak J Stat 32(1): 1-20.
- BALAKRISHNAN N. 2014. Methods and Applications of Statistics in Clinical Trials: Planning, Analysis and Inferential Methods. J Wiley & Sons, Inc.
- BLISS CI AND FISHER RA. 1953. Fitting the negative binomial distribution to biological data. Biometrics 9(2): 176-200.
- CASTILLO I AND PEREZ-CASANY M. 1998. Weighted Poisson distributions for overdispersion and underdispersion situations. Ann Inst Statist Math 50: 567-585.
- CHAKRABORTY S AND CHAKRAVARTY D. 2012. Discrete gamma distributions: Properties and parameter estimations. Commun Statist Theor Meth 41: 3301-3324.
- DENUIT M, MARCHAL X, PITREBOIS S AND WALHIN JF. 2007. Actuarial Modelling of Claim Counts Risk Classification Credibility and Bonus-Malus Systems. John Wiley.
- FALLS L, WILLIFORD WO AND CARTER MC. 1971. Probability distributions for thunderstorm activity at Cape Kennedy, Florida. J Appl Meteorol 10: 97-104.
- FISHER RA. 1934. The effects of methods of ascertainment upon the estimation of frequencies. Ann Eugenic 6: 13-25.
- GARMAN P. 1951. Original data on European red mite on apple leaves. Technical report. Report. Connecticut.
- GREENWOOD M AND WOODS HM. 1919. The Incidence of Industrial Accidents upon Individuals with Special Reference to Multiple Accidents. Industrials Fatigue Research Board Report URL https://ia802705.us.archive.org/29/items/ncidenceofindus00grea/incidenceofindus00grea.pdf. Online Address.
» https://ia802705.us.archive.org/29/items/ncidenceofindus00grea/incidenceofindus00grea.pdf. - GREENWOOD M AND YULE GU. 1920. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. J Roy Stat Soc 83: 255-279.
- HUSSAIN T, ASLAM M AND AHMAD M. 2016. A two parameter discrete Lindley distribution. Rev Colomb Estad 39: 45-61.
- JAIN GC AND CONSUL PC. 1971. A generalized negative binomial distribution. SIAM J Appl Math 21: 501-5013
- JAIN K, SINGLA N AND GUPTA RD. 2014. A weighted version of gamma distribution. Discus Math Prob Stat 34: 89-111.
- KENDALL MG. 1961. Natural law in social sciences. J R Stat Soc Ser A 124: 1-19.
- KHAN AMS, KHALIQUE A AND ABOUAMMOTH AM. 1989. On estimating parameters in a discrete Weibull distribution. IEEE T Reliab 38: 348-350.
- KOKONENDJI CC AND CASANY MP. 2012. A note on weighted count distributions. J Stat Theory Appl 11: 337-352.
- KOKONENDJI CC AND MIZRE D. 2005. Overdispersion and Underdispersion Characterization of Weighted Poisson Distribution (Technical Report No. 0523) France LMA. Technical report.
- NEEL JV AND SCHULL WJ. 1966. Human Heredity. Chicago: University of Chicago Press.
- PATIL GP. 1991. Encountered data, statistical ecology, environmental statistics, and weighted distribution methods. Environmetrics 2: 377-423.
- PATIL GP AND RAO CR. 1977. Weighted distributions: a survey of their application. In Krishnaiah PR (Ed.), Applications of Statistics, pp. 383-405. North Holland Publishing Company.
- PATILL GP, RAO CR AND RATNAPARKHI M. 1986. On discrete weighted distribution and their use in model choice for observed data. Commun Statisit Theory Math 15: 907-918.
- RAO CR. 1985. Weighted distributions arising out of methods of ascertainment. In Atkinson AC AND Fienberg SE (Eds.), A Celebration of Statistics Chapter 24. pp. 543-569. New York: Springer-Verlag.
- RIDOUT MS AND BESBEAS P. 2004. An empirical model for under dispersed count data. Statist Model 4: 77-89.
- ROHATGI VK AND SALEH AKE. 2002. An Introduction to probability and Statistics. Singapore: John Wiley and Sons (Asia) Pte Ltd.
- ROSS GJS AND PREECE DA. 1985. The negative binomial distribution. The Statistician 34: 323-336.
- SAENGTHONG P AND BODHISUWAN W. 2013. Negative binomial-crack (NB-CR) distribution. Int J Pure Appl Math 84: 213-230.
- SAKAMOTO CM. 1973. Application of the Poisson and negative binomial models to thunderstorm and hail days probabilities in Nevada. Monthly Weather Review 101: 350-355.
- STEUTEL FW AND VAN HARN K. 1979. Discrete analogues of self-decomposability and stability. Ann Prob 7: 893-899.
- VUONG QH. 1989. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 57: 307-333.
APPENDIX
Frequencies of the observed number of days that experience x TH’s at Cape Kennedy,Fla.,for 11-year period of Record January 1957 through December 1967.
Expected Frequencies,Log Likelihood, x2,AIC and p-values of the observed number of days that experience x TH’s at Cape Kennedy,Fla.,from WNBDL.
Expected Frequencies,Log Likelihood, x2,AIC and p-values of the Observed number of days that experience x TH’s at Cape Kennedy,Fla.,from NB.
Publication Dates
-
Publication in this collection
Jul-Sep 2018
History
-
Received
18 Sept 2017 -
Accepted
05 Jan 2018