ABSTRACT
An asymmetric membrane of polysulfone (PSf) was synthesized by phase inversion method. Permeation experiments were carried out between 2 to 5 bar pressure, and at temperatures 20 to 45°C. The dense-selective layer of PSf membrane presents regular thickness (about 5 µm), and was not possible to observe the formation of macrovoids in porous layer. The CO2 permeability through membrane was 18.8 Barrer at 35°C and 2 bar pressure, and this relationship between the pressure and the CO2 permeability was described adequately by Dual-mode model. The absence of CH4 permeability at 2 and 3 bar pressure, qualifies the PSf membrane for gases separation with high selectivity in this range.
Key words:
asymmetric membranes; CO2/CH4 permeability; Dual-mode model; polysulfone
INTRODUCTION
Currently, there is a need in the world to substitute fossil fuels for renewable sources in the energy production. Natural gas has significant advantages over other fossil fuels, in particular the reduction in atmospheric emissions from their combustion. Concentrations of sulfur oxides (SOx) and particulate matter are low in flue gas produced by natural gas combustion.
Biogas consists mainly of methane (CH4), carbon dioxide (CO2) and water (H2O), having other trace compounds (H2S, siloxane, VOC’s, NH3, O2, CO and N2) in its composition. Biogas is a combination of chemical species produced in the organic matter degradation process. Biogas is produced in landfills, anaerobic reactors, pyrolysis reactors, among others. The use of methane, present in biogas, is a renewable alternative instead of using natural gas in its various applications. The biomethane is obtained from the removal of carbon dioxide and water, besides trace components present in the biogas, and has in its composition from 95 % to 97 % (vol/vol) of methane (Krich et al. 2005KRICH K, AUGENSTEIN D, BATMALE JP, BENEMANN J, RUTLEDGE B AND SALOUR D. 2005. Upgrading Dairy Biogas to Biomethane and Other Fuels. In: Andrews K (Ed), Biomethane from Dairy Waste - A Sourceb Use Renew Nat Gas California. California: Clear Concepts, p. 47-69., Ryckebosch et al. 2011RYCKEBOSCH E, DROUILLON M AND VERVAEREN H. 2011. Techniques for transformation of biogas to biomethane. Biomass Bioenergy 35: 1633-1645., Chen et al. 2015CHEN XY, VINH-THANG H, RAMIREZ AA, RODRIGUE D AND KALIAGUINE S. 2015. Membrane gas separation technologies for biogas upgrading. RSC Adv 5: 24399-24448.). Within this context, polymeric membranes for methane gas purify, have received great attention due to several advantages, such as energy efficiency in operation and low environmental impact regarding to other technologies (Basu et al. 2010aBASU S, KHAN AL, CANO-ODENA A, LIU C AND VANKELECOM IFJ. 2010a. Membrane-based technologies for biogas separations. Chem Soc Rev 39: 750-768.). Polymeric membranes have been studied for separating CO2 (Wang et al. 2002WANG R, CHAN SS, LIU Y AND CHUNG TS. 2002. Gas transport properties of poly(1,5-naphthalene-2,2 ’-bis (3,4-phthalic) hexafluoropropane) diimide (6FDA-1,5-NDA) dense membranes. J Memb Sci 199: 191-202., Qin et al. 2005QIN JJ, CHUNG TS, CAO C AND VORA RH. 2005. Effect of temperature on intrinsic permeation properties of 6FDA-Durene/1,3-phenylenediamine (mPDA) copolyimide and fabrication of its hollow fiber membranes for CO2/CH4 separation. J Memb Sci 250: 95-103., Husken et al. 2010HUSKEN D, VISSER T, WESSLING M AND GAYMANS RJ. 2010. CO2 permeation properties of poly(ethylene oxide)-based segmented block copolymers. J Memb Sci 346: 194-201., Minelli et al. 2013MINELLI M, BASCHETTI MG, HALLINAN DT AND BALSARA NP. 2013. Study of gas permeabilities through polystyrene-block-poly(ethylene oxide) copolymers. J Memb Sci 432: 83-89., Saedi et al. 2013SAEDI S, MADAENI SS, HASSANZADEH K, SHAMSABADI AA AND LAKI S. 2013. The effect of polyurethane on the structure and performance of PES membrane for separation of carbon dioxide from methane. J Ind Eng Chem 20: 1916-1929.). One of the most investigated polymers (Hu et al. 2003, Ismail and Lai 2004ISMAIL AF AND LAI PY. 2004. Development of defect-free asymmetric polysulfone membranes for gas separation using response surface methodology. Sep Purif Technol 40: 191-207., Gabelman and Hwang 2005GABELMAN A AND HWANG ST. 2005. Experimental results versus model predictions for dense gas extraction using a hollow fiber membrane contactor. J Supercrit Fluids 35: 26-39., Aroon et al. 2010AROON MA, ISMAIL AF, MONTAZER-RAHMATI MM AND MATSUURA T. 2010. Morphology and permeation properties of polysulfone membranes for gas separation: Effects of non-solvent additives and co-solvent. Sep Purif Technol 72:194-202., Scholes et al. 2010SCHOLES CA, CHEN GQ, STEVENS GW AND KENTISH SE. 2010. Plasticization of ultra-thin polysulfone membranes by carbon dioxide. J Memb Sci 346: 208-214., 2012, Julian and Wenten 2012JULIAN H AND WENTEN IG. 2012. Polysulfone membranes for CO2/CH4 separation: State of the art. IOSR J Eng 2: 484-495., Hölck et al. 2013HÖLCK O, BÖHNING M, HEUCHEL M, SIEGERT MR AND HOFMANN D. 2013. Gas sorption isotherms in swelling glassy polymers-Detailed atomistic simulations. J Memb Sci 428: 523-532., Robeson et al. 2014ROBESON LM, SMITH ZP, FREEMAN BD AND PAUL DR. 2014. Contributions of diffusion and solubility selectivity to the upper bound analysis for glassy gas separation membranes. J Memb Sci 453: 71-83., Chen et al. 2015) for the separation of CO2 is polysulfone (PSf). PSf has low cost regarding to others high performance polymers, has high chemical resistance (acid, alkali, salt solutions, detergents, oils and alcohols) and good mechanical properties. Blends of PSf with others polymers and inorganic materials have being also evaluated for the separation of CO2 (Qin and Chung 2006, Ahn et al. 2008AHN J, CHUNG WJ, PINNAU I AND GUIVER MD. 2008. Polysulfone/silica nanoparticle mixed-matrix membranes for gas separation. J Memb Sci 314: 123-133., Basu et al. 2010b, Deng and Hägg 2010DENG L AND HÄGG MB. 2010. Techno-economic evaluation of biogas upgrading process using CO2 facilitated transport membrane. Int J Greenh Gas Control 4: 638-646., Rafiq et al. 2012RAFIQ S, MAN Z, MAULUD A, MUHAMMAD N AND MAITRA S. 2012. Separation of CO2 from CH4 using polysulfone/ polyimide silica nanocomposite membranes. Sep Purif Technol 90: 162-172., Eiras et al. 2016EIRAS D, LABRECHE Y AND PESSAN LA. 2016. Ultem®/ZIF-8 Mixed Matrix Membranes for Gas Separation: Transport and Physical Properties. Mater Res 19: 220-228.). The phase inversion is a process widely used for the synthesis of polymeric membranes. Several solvents (McHattie et al. 1991, Ghosal et al. 1996GHOSAL K, CHERN RT, FREEMAN BD, DALY WH AND NEGULESCU II. 1996. Effect of Basic Substituents on Gas Sorption and Permeation in Polysulfone. Macromolecules 29: 4360-4369., Feng et al. 2002FENG X, SHAO P, HUANG RYM, JIANG G AND XU R-X. 2002. A study of silicone rubber/polysulfone composite membranes: correlating H2/N2 and O2/N2 permselectivities. Sep Purif Technol 27: 211-223., Wang et al. 2002, Hu et al. 2003, Ismail and Hassan 2006, Conesa et al. 2007CONESA A, GUMÍ T AND PALET C. 2007. Membrane thickness and preparation temperature as key parameters for controlling the macrovoid structure of chiral activated membranes (CAM). J Memb Sci 287: 29-40., Ahn et al. 2008, Chakrabarty et al. 2008CHAKRABARTY B, GHOSHAL AK AND PURKAIT MK. 2008. Effect of molecular weight of PEG on membrane morphology and transport properties. J Memb Sci 309: 209-221., Kim and Marand 2008KIM S AND MARAND E. 2008. High permeability nano-composite membranes based on mesoporous MCM-41 nanoparticles in a polysulfone matrix. Microporous Mesoporous Mater 114: 129-136., Aroon et al. 2010) have being used in the synthesis of polymeric membranes: 1-methyl-2-pyrrolidone (NMP), tetrahydrofuran (THF), N,N′-dimethylacetamide (DMAc), hexamethylphosphoramide (HMPA), trimethylphosphate (TMP), triethylphosphate (TEP), N,N’-dimethylformamide (DMF), chloroform and methylene chloride.
However, few studies are reported in the literature for the separation of CO2 from PSf membranes at low pressures (up to 5 bar) as well as data on the influence of temperature on the performance of the separation process.
In the present work, a detailed study on the performance of a PSf membrane for the separation of CO2 in a range of low pressure and different temperatures was performed.
MATERIALS AND METHODS
PREPARATION OF ASYMMETRIC MEMBRANES
The preparation of PSf membrane was conducted according to the phase inversion process by immersion-precipitation method (Godinho et al. 2016GODINHO M, BIONDO L, DUARTE J AND ZENI M. 2016. Processo de obtenção de membrana polimérica, assimétrica porosa, membrana polimérica e método de separação de gases. Brasil, INPI - BR 10 2016 0182140.). PSf (30 %) used in the membrane synthesis was supplied by Sigma-Aldrich in the form of pellets and molecular weight of 35,000 g.mol-1. The solvents used in the synthesis were N, N’-dimethylformamide (DMF) and 1-methyl-2-pyrrolidone (NMP), molar mass of 73.1 g.mol-1 and 99.13 g.mol-1, respectively, with saturation pressure of 2.7 mmHg (DMF) and 0.29 mmHg (NMP) at 20°C. Distilled water and analytical standard ethyl alcohol were used as non-solvent in the synthesis. The gases (CO2 and CH4) used in the permeation tests have 99.99 % purity, supplied by Air Products.
CHARACTERIZATION AND GAS TRANSPORT MEASUREMENTS
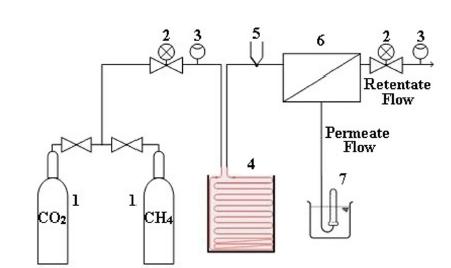
CO2 and CH4 pure were singly tested under varying conditions of pressure (from 2 to 5 bar) and temperature (from 20 to 45°C), in triplicate according to the Figure 1. In order to avoid the hysteretic effects that can be caused by exposure to high-pressure gases, a procedure to avoid time dependence was conducted. After the membrane installation in the permeation cell, it has been subjected to a CO2 flux for a period of 3 hours at a 5 bar pressure, 20°C temperature and 1L.min-1 flow rate. The permeation tests were performed on the pressure range from 2 to 5 bar, and temperatures from 20 to 45°C. The gas stream (feed) is introduced into the permeation cell (Figure 1:6) perpendicularly, and the concentrated gas stream (discard), flows tangentially into the permeation cell. The permeate gas flow is measured by bolhometer (Figure 1:7) as a time (stopwatch) function. The pressure and flow of the concentrated stream were also monitored. The interval time between each triplicate point was 20 min, for each temperature worked at each pressure. For each triplicate point, six measures were performed with fixed volume and recording the time of each measurement. If the time difference between any of the averages varied between 2 and 5 s, the measurements were restarted. After all, with both gases, the membranes were again subjected to the test from 2 to 5 bar of pressure with temperature to 20°C, in order to identify possible deviations. Significant reductions (up to 70 %) were observed in permeability during the procedure.
Gas Permeation System. 1 - Feed gas cylinder; 2 - Pressure controller valve; 3 - Rotameter; 4 - Thermostatic bath; 5 - Thermocouple; 6 - Permeation cell; 7 - Soap bubble flow meter.
Scanning Electron Microscopy (SEM) using a Shimadzu, model SSX-550 was used to examine the morphology and thickness of the membranes. Samples were fractured in liquid nitrogen and metalized with a thin gold layer by sputtering process with an exposure time of 2 min.
RESULTS AND DISCUSSION
PERMEATION PROPERTIES OF SINGLE PURE GASES
In a system where a gas diffuses through a membrane, the flux is usually described by Equation 1:
where: Ji is the flux of specie i (m³(STP).m-2.h-1), Pi is the permeability of specie i (m³(STP).m.m-2.h-1.bar-1), Pa and Pp - are the pressures in the feed and permeate (bar) and 1 is the membrane thickness (m).
The permeability in nonporous dense polymeric membranes can be described by the solution-diffusion mechanism, described by Equation 2 (Pauly 1999PAULY S. 1999. Permeability and diffusion data. In: J Brandrup, E H Immergut EAG, organizador. Polym Handb. 4th ed., New York: J Wiley & Sons Inc., p. 543-569., Chen et al. 2015CHEN XY, VINH-THANG H, RAMIREZ AA, RODRIGUE D AND KALIAGUINE S. 2015. Membrane gas separation technologies for biogas upgrading. RSC Adv 5: 24399-24448.):
where: D is the diffusivity coefficient (m².s-1) and S is the solubility coefficient (m³ (STP). m-3 polymer).
According to Arrhenius equation, the permeability (P) of a gas in a polymer is related to the temperature over the activation energy of permeation (EP) and can be expressed according to Equation 3.
where: Po is the pre-exponential factor (Barrer), and EP is the activation energy of permeation (kJ∙mol-1).
The membrane ability to separate two gases (i and j) is the ratio of their permeability, known by selectivity (αij), and represented by Equation 4.
Relationship between pressure and the gas permeability through the PSf membrane is shown in Figure 2.
The permeability observed for the PSf membranes are typical for CO2 separation, where the gas transport control occurs in the dense layer (solution-diffusion mechanism). McHattie et al. (1991) obtained results of CO2 permeability in a PSf membrane similar, i.e., a smooth reduction in permeability with increasing pressure. This behavior is typical for the Dual- mode model, since the permeability of a gas molecules is dependent of the free volume available in the polymer matrix and the gas condensability (Langmuir mode), as well as, the gas-polymer interaction (Henry’s mode). However, under low pressures (2 and 3 bar), the Langmuir mode preferentially governs the transport mechanism, favoring the permeability of CO2, to CH4, due to its kinetic diameter, 3.3 Å and 3.8 Å respectively, until free volume saturation. From increment operating pressure, the Henry’s mode preferentially governs the transport mechanism, favoring the permeability of CH4, to CO2, since those larger molecules are generally more condensable, increasing the gas-polymer interaction. Selectivity at 3 and 4 bar were 5.1 and 4.6, respectively. It was not observed CH4 permeability for 2 and 3 bar pressures, while between 3 and 4 bar there was a little increased in your permeability. Absence of CH4 permeability was observed for all temperatures evaluated. Such lack of permeability may be related to free volume in the selective layer of the membrane. In general, a polymer with a low free volume fraction has a high degree of crystallinity (Sweed 2011SWEED MA. 2011. Free volume properties of semi-crystalline polymers. Ph.D. dissertation Stellenbosch University, South Africa.). According Kholodovych and Welsh (2007KHOLODOVYCH V AND WELSH WJ. 2007. Densities of Amorphous and Crystalline Polymers. Physical Properties of Polymers Handbook, Springer, New York, NY, p. 611-617.) polymer chains are more packed in the crystalline region than in the amorphous regions of the polymer, and consequently the density of the crystalline region is larger than in the amorphous region. The molecular orientation may also have been caused during the spreading of the polymeric solution during synthesis by phase inversion process, causing an increase in the degree of crystallinity of the polymer. Given that there was no methane permeability between 2 and 3 bar, it is a region suitable for the gases separation. Figure 3 shows the SEM photomicrograph of the PSf membrane cross section.
The dense-selective layer shows regular thickness along the membrane (about 5 µm), while its total thickness is approximately 90 µm. On the porous layer of the membrane is not possible to observe the formation of macrovoids.
Figure 4 shows the temperature effect on CO2 permeability.
The activation energies of CO2 permeation in the membrane were 6.89, 5.52, 5.24 and 5.09 kJ∙mol-1 for feed pressures of 2, 3, 4 and 5 bar, respectively. Permeability increases with increasing temperature for all pressures evaluated. Such behavior is expected below of glass transition temperature of the polymer (Tg = 186?C). The activation energy of CO2 permeation indicates affinity between CO2 molecules and the membrane. Therefore, the activation energies obtained indicated a decreasing affinity between CO2 molecules and the membrane, as increases pressure. Decreased activation energy with increased pressure is an indicative of the larger contribution of solubility to the permeation mechanism at higher pressures (Godinho et al. 2016GODINHO M, BIONDO L, DUARTE J AND ZENI M. 2016. Processo de obtenção de membrana polimérica, assimétrica porosa, membrana polimérica e método de separação de gases. Brasil, INPI - BR 10 2016 0182140.).
DUAL-MODE ANALYSIS
According to the Dual-mode model, gas sorption in glassy polymers can be described as a function of pressure by Equation 5:
where: CD (cm³(STP).cm-3) and CH (cm³(STP).cm-3) represent Henry’s Law mode sorption and Langmuir mode sorption, respectively. The parameter kD is the Henry’s law solubility coefficient, (cm³(STP).cm-3), C’H is the Langmuir sorption capacity (cm³(STP).cm-3), b is an affinity parameter characterizing the ratio constants for sorption and desorption (atm-1) and Pa is the feed pressure.
There is a diffusion constant associated with each mode sorption (Henry and Langmuir), considering the existence of permanent spaces between polymer chains (interstitial free volume), and transient due to thermal movement of the material (Koros et al. 1976KOROS WJ, PAUL DR AND ROCHA AA. 1976. Carbon dioxide sorption and transport in polycarbonate. J Polym Sci Polym Phys 14: 687-702., 1978, Kanehashi and Nagai 2005KANEHASHI S AND NAGAI K. 2005. Analysis of dual-mode model parameters for gas sorption in glassy polymers. J Memb Sci 253: 117-138.). Permeability (P) can be represented as the sum of the Henry’s mode and the Langmuir mode as described in Equation 6:
where: DH is the diffusivity coefficient regarding to Langmuir mode and DD is the diffusivity coefficient regarding to Henry’s Law mode.
Permeability obtained for the PSf membrane was evaluated in the Dual-mode model. For this purpose, model constants obtained by other authors (McHattie et al. 1991, Hu et al. 2003HU CC, CHANG CS, RUAAN RC AND LAI JY. 2003. Effect of free volume and sorption on membrane gas transport. J Memb Sci 226: 51-61., Scholes et al. 2010SCHOLES CA, CHEN GQ, STEVENS GW AND KENTISH SE. 2010. Plasticization of ultra-thin polysulfone membranes by carbon dioxide. J Memb Sci 346: 208-214.) for the CO2 permeation in PSf membranes were used. The constants were obtained at 35°C, and are presented in Table I.
Figure 5 shows the experimental permeability obtained in this work, and the results predicted by the Dual-mode model. The membrane used in this work was synthesized from two solvents (DMF/NMP), while constants used for the Dual-mode model were derived from different solvents. The experimental permeability was higher than those predicted from Dual-mode model, although behavior of permeability as function pressure was similar to that predicted by the model, suggesting that gas transport in the membrane is controlled in the dense-selective layer according to the Henry’s and Langmuir models.
SOLUBILITY AND DIFFUSIVITY CONTRIBUTIONS
Robeson et al. 2014ROBESON LM, SMITH ZP, FREEMAN BD AND PAUL DR. 2014. Contributions of diffusion and solubility selectivity to the upper bound analysis for glassy gas separation membranes. J Memb Sci 453: 71-83. established empirical equations 7 and 8 to correlate the solubility (S) and diffusivity (D) coefficients to permeability (P) in glassy polymeric membranes, obtained from permeation tests of CO2 at temperatures from 25 to 35°C at 2 bar.
where: SCO2 is the solubility coefficient of CO2 (cm³ (STP).cm-3), DCO2 is the diffusivity coefficient of CO2 (cm².s-1), and PCO2 is the permeability coefficient of CO2 (cm³(STP).cm .cm-2.s-1.cmHg-1).
Permeabilities obtained in this work were applied to the equations, in order to estimate the diffusivity and solubility coefficients for PSf membrane. Figure 6 shows the solubility coefficients for the PSf membrane.
There was a significant increase in the solubility coefficient with increasing pressure. Wang and Kamiya (1995WANG JS AND KAMIYA Y. 1995. Concurrent measurements of sorption and dilation isotherms and diffusivity for polysulfone membrane/carbon dioxide system. J Memb Sci 98: 69-76.), Scholes et al. (2010SCHOLES CA, CHEN GQ, STEVENS GW AND KENTISH SE. 2010. Plasticization of ultra-thin polysulfone membranes by carbon dioxide. J Memb Sci 346: 208-214.) and Li et al. (2014LI P, CHUNG TS AND PAUL DR 2014. Temperature dependence of gas sorption and permeation in PIM-1. J Memb Sci 450: 380-388.) observed a similar trend in their studies. The solubility coefficient is influenced by gas condensability, interactions between polymer and gas and the free volume in the polymeric matrix. The gas condensability increases with increasing its critical temperature, consequently increasing the solubility coefficient. The saturation temperature of CO2 at 2 bar is approximately 205 K (- 68°C), while at 5 bar, it is approximately 218 K (- 55°C). Thus, in the temperature range evaluated in this study, there is no possibility of CO2 condensation in the polymeric matrix. The gas-polymer interaction is significant for the Henry’s mode, while gas condensability and the free volume in the polymer are significant to the Langmuir mode. At low pressures, the Langmuir mode has a higher influence on the solubility coefficient than Henry mode. Regarding the impossibility of condensation of CO2 in the polymer matrix, the influence of free volume is the determining factor considered in the analysis of solubility coefficient.
Robeson et al. (2014ROBESON LM, SMITH ZP, FREEMAN BD AND PAUL DR. 2014. Contributions of diffusion and solubility selectivity to the upper bound analysis for glassy gas separation membranes. J Memb Sci 453: 71-83.) presented the Equation 9 to determine the diffusivity coefficient in steady state (Dsec). Such equation is obtained from Equations 5 and 6, considering the Dual-mode model.
Where: Ssec is the solubility coefficient in steady state.
Figure 7 shows the predicted values of diffusivity coefficient from Equations 8 and 9. The Dual-mode model constants applied in Equation 9 were obtained by Hu et al. 2003HU CC, CHANG CS, RUAAN RC AND LAI JY. 2003. Effect of free volume and sorption on membrane gas transport. J Memb Sci 226: 51-61. for chloroform at 35°C.
The diffusivity coefficients showed a typical behavior for the permeation of non-condensable gases in non-porous polymeric membrane (Basile and Nunes 2011BASILE A AND NUNES S. 2011. Advanced Membrane Science and Technology for Sustainable Energy and Environmental Applications. 25th ed., Woodhead Publishing Limited. United Kingdom, p. 718-745.). According to the Table I, C?Hb is higher KD, which means that the Langmuir sorption is more important than the Henry sorption in Dual-mode model. Langmuir mode is more sensitive to pressure than the Henry mode. Therefore, diffusivity behavior according to the Equation 9 is in agreement with the predicted by the Dual-mode model. Equation 8 is an experimental data fit, and the diffusivity behavior is associated with permeability (P), i.e., diffusivity has the same behavior of the permeability measured from Equation 1.
Figures 8 and 9 present the behavior of the solubility and diffusivity coefficients in function of temperature.
Regarding to temperature influence on solubility coefficient, with its increase, there is a reduction in the permanent free volume (microvoids present in the dense layer, related to the Langmuir mode) due to the thermal rearrangement of the polymer chains, thus reducing the solubility coefficient of the Langmuir mode. Similar results were found by Wang and Kamiya (1995WANG JS AND KAMIYA Y. 1995. Concurrent measurements of sorption and dilation isotherms and diffusivity for polysulfone membrane/carbon dioxide system. J Memb Sci 98: 69-76.). At same time, increasing temperature, there is an increase in the solubility coefficient related to Henry’s mode, due to the higher activation energy of permeation responsible for increase transient voids (intersegmental spaces), resulting in higher sorption by the Henry’s mode. In fact, within the temperature range studied the modes are practically compensated, with no significant influence on the solubility. However, the diffusion coefficient increases with increasing operating temperature, according Magnanelli et al. (2016MAGNANELLI E, WILHELMSEN Ø, JOHANNESSEN E AND KJELSTRUP S. 2016. Enhancing the understanding of heat and mass transport through a cellulose acetate membrane for CO2 separation. J Memb Sci 513: 129-139.), this is because the membrane not be supported. The increase in temperature increases the vibrational energy in the polymeric chains, therefore increases the activation energy of permeation for the molecules perform the diffusive jumps within the transient spaces by Langmuir mode (sorbed molecules in the permanent free volume of the polymeric matrix) and through Henry’s mode (sorbed molecules in the intersegmental spaces in the polymeric chains).
CONCLUSIONS
The CO2 permeability though membrane ranged since 18.8 Barrer at 2 pressure until 15.4 Barrer at 5 bar pressure (35?C), presenting a smooth reduction in permeability with increasing pressure, especially above 3 bar pressure. It was not observed CH4 permeability for 2 and 3 bar pressure (35?C), while between 3 and 4 bar there was a little increased in your permeability (from 3.1 to 3.3 Barrer). The CO2 permeability’s behavior was similar to that predicted by the Dual-mode model, although the permeability predicted by model has been lower than the experimental values.
The activation energy of CO2 permeation in the membrane decreases with increased pressure, i.e., permeability increases with increasing temperature for all pressures evaluated.
The absence of methane permeability at 2 and 3 bar pressure, qualifies the membrane for the separation of gases with high selectivity in this range.
REFERENCES
- AHN J, CHUNG WJ, PINNAU I AND GUIVER MD. 2008. Polysulfone/silica nanoparticle mixed-matrix membranes for gas separation. J Memb Sci 314: 123-133.
- AROON MA, ISMAIL AF, MONTAZER-RAHMATI MM AND MATSUURA T. 2010. Morphology and permeation properties of polysulfone membranes for gas separation: Effects of non-solvent additives and co-solvent. Sep Purif Technol 72:194-202.
- BASILE A AND NUNES S. 2011. Advanced Membrane Science and Technology for Sustainable Energy and Environmental Applications. 25th ed., Woodhead Publishing Limited. United Kingdom, p. 718-745.
- BASU S, KHAN AL, CANO-ODENA A, LIU C AND VANKELECOM IFJ. 2010a. Membrane-based technologies for biogas separations. Chem Soc Rev 39: 750-768.
- BASU S, CANO-ODENA A AND VANKELECOM IFJ. 2010b. Asymmetric membrane based on Matrimid® and polysulphone blends for enhanced permeance and stability in binary gas (CO 2/CH4) mixture separations. Sep Purif Technol 75: 15-21.
- CHAKRABARTY B, GHOSHAL AK AND PURKAIT MK. 2008. Effect of molecular weight of PEG on membrane morphology and transport properties. J Memb Sci 309: 209-221.
- CHEN XY, VINH-THANG H, RAMIREZ AA, RODRIGUE D AND KALIAGUINE S. 2015. Membrane gas separation technologies for biogas upgrading. RSC Adv 5: 24399-24448.
- CONESA A, GUMÍ T AND PALET C. 2007. Membrane thickness and preparation temperature as key parameters for controlling the macrovoid structure of chiral activated membranes (CAM). J Memb Sci 287: 29-40.
- DENG L AND HÄGG MB. 2010. Techno-economic evaluation of biogas upgrading process using CO2 facilitated transport membrane. Int J Greenh Gas Control 4: 638-646.
- EIRAS D, LABRECHE Y AND PESSAN LA. 2016. Ultem®/ZIF-8 Mixed Matrix Membranes for Gas Separation: Transport and Physical Properties. Mater Res 19: 220-228.
- FENG X, SHAO P, HUANG RYM, JIANG G AND XU R-X. 2002. A study of silicone rubber/polysulfone composite membranes: correlating H2/N2 and O2/N2 permselectivities. Sep Purif Technol 27: 211-223.
- GABELMAN A AND HWANG ST. 2005. Experimental results versus model predictions for dense gas extraction using a hollow fiber membrane contactor. J Supercrit Fluids 35: 26-39.
- GHOSAL K, CHERN RT, FREEMAN BD, DALY WH AND NEGULESCU II. 1996. Effect of Basic Substituents on Gas Sorption and Permeation in Polysulfone. Macromolecules 29: 4360-4369.
- GODINHO M, BIONDO L, DUARTE J AND ZENI M. 2016. Processo de obtenção de membrana polimérica, assimétrica porosa, membrana polimérica e método de separação de gases. Brasil, INPI - BR 10 2016 0182140.
- HÖLCK O, BÖHNING M, HEUCHEL M, SIEGERT MR AND HOFMANN D. 2013. Gas sorption isotherms in swelling glassy polymers-Detailed atomistic simulations. J Memb Sci 428: 523-532.
- HU CC, CHANG CS, RUAAN RC AND LAI JY. 2003. Effect of free volume and sorption on membrane gas transport. J Memb Sci 226: 51-61.
- HUSKEN D, VISSER T, WESSLING M AND GAYMANS RJ. 2010. CO2 permeation properties of poly(ethylene oxide)-based segmented block copolymers. J Memb Sci 346: 194-201.
- ISMAIL AF AND HASSAN AR. 2006. Formation and characterization of asymmetric nanofiltration membrane: Effect of shear rate and polymer concentration. J Memb Sci 270: 57-72.
- ISMAIL AF AND LAI PY. 2004. Development of defect-free asymmetric polysulfone membranes for gas separation using response surface methodology. Sep Purif Technol 40: 191-207.
- JULIAN H AND WENTEN IG. 2012. Polysulfone membranes for CO2/CH4 separation: State of the art. IOSR J Eng 2: 484-495.
- KANEHASHI S AND NAGAI K. 2005. Analysis of dual-mode model parameters for gas sorption in glassy polymers. J Memb Sci 253: 117-138.
- KHOLODOVYCH V AND WELSH WJ. 2007. Densities of Amorphous and Crystalline Polymers. Physical Properties of Polymers Handbook, Springer, New York, NY, p. 611-617.
- KIM S AND MARAND E. 2008. High permeability nano-composite membranes based on mesoporous MCM-41 nanoparticles in a polysulfone matrix. Microporous Mesoporous Mater 114: 129-136.
- KOROS WJ AND PAUL DR. 1978. Transient and steady-state permeation in poly(ethylene terephthlate) above and below the glass transition. J Polym Sci Polym Phys 16: 2171-2187.
- KOROS WJ, PAUL DR AND ROCHA AA. 1976. Carbon dioxide sorption and transport in polycarbonate. J Polym Sci Polym Phys 14: 687-702.
- KRICH K, AUGENSTEIN D, BATMALE JP, BENEMANN J, RUTLEDGE B AND SALOUR D. 2005. Upgrading Dairy Biogas to Biomethane and Other Fuels. In: Andrews K (Ed), Biomethane from Dairy Waste - A Sourceb Use Renew Nat Gas California. California: Clear Concepts, p. 47-69.
- LI P, CHUNG TS AND PAUL DR 2014. Temperature dependence of gas sorption and permeation in PIM-1. J Memb Sci 450: 380-388.
- MAGNANELLI E, WILHELMSEN Ø, JOHANNESSEN E AND KJELSTRUP S. 2016. Enhancing the understanding of heat and mass transport through a cellulose acetate membrane for CO2 separation. J Memb Sci 513: 129-139.
- MCHATTIE JS, KOROS WJ AND PAUL DR. 1991. Gas transport properties of polysulfones. 1. Role of symmetry of methyl group placement on bisphenol. Polymer (Guildf) 32: 840-850.
- MINELLI M, BASCHETTI MG, HALLINAN DT AND BALSARA NP. 2013. Study of gas permeabilities through polystyrene-block-poly(ethylene oxide) copolymers. J Memb Sci 432: 83-89.
- PAULY S. 1999. Permeability and diffusion data. In: J Brandrup, E H Immergut EAG, organizador. Polym Handb. 4th ed., New York: J Wiley & Sons Inc., p. 543-569.
- QIN JJ AND CHUNG TS. 2006. Development of high-performance polysulfone / poly (4-vinylpyridine) composite hollow fibers for CO2/CH4 separation. Desalination 192: 112-116.
- QIN JJ, CHUNG TS, CAO C AND VORA RH. 2005. Effect of temperature on intrinsic permeation properties of 6FDA-Durene/1,3-phenylenediamine (mPDA) copolyimide and fabrication of its hollow fiber membranes for CO2/CH4 separation. J Memb Sci 250: 95-103.
- RAFIQ S, MAN Z, MAULUD A, MUHAMMAD N AND MAITRA S. 2012. Separation of CO2 from CH4 using polysulfone/ polyimide silica nanocomposite membranes. Sep Purif Technol 90: 162-172.
- ROBESON LM, SMITH ZP, FREEMAN BD AND PAUL DR. 2014. Contributions of diffusion and solubility selectivity to the upper bound analysis for glassy gas separation membranes. J Memb Sci 453: 71-83.
- RYCKEBOSCH E, DROUILLON M AND VERVAEREN H. 2011. Techniques for transformation of biogas to biomethane. Biomass Bioenergy 35: 1633-1645.
- SAEDI S, MADAENI SS, HASSANZADEH K, SHAMSABADI AA AND LAKI S. 2013. The effect of polyurethane on the structure and performance of PES membrane for separation of carbon dioxide from methane. J Ind Eng Chem 20: 1916-1929.
- SCHOLES CA, CHEN GQ, STEVENS GW AND KENTISH SE. 2010. Plasticization of ultra-thin polysulfone membranes by carbon dioxide. J Memb Sci 346: 208-214.
- SCHOLES CA, STEVENS GW AND KENTISH SE. 2012. Membrane gas separation applications in natural gas processing. Fuel 96: 15-28.
- SWEED MA. 2011. Free volume properties of semi-crystalline polymers. Ph.D. dissertation Stellenbosch University, South Africa.
- WANG JS AND KAMIYA Y. 1995. Concurrent measurements of sorption and dilation isotherms and diffusivity for polysulfone membrane/carbon dioxide system. J Memb Sci 98: 69-76.
- WANG R, CHAN SS, LIU Y AND CHUNG TS. 2002. Gas transport properties of poly(1,5-naphthalene-2,2 ’-bis (3,4-phthalic) hexafluoropropane) diimide (6FDA-1,5-NDA) dense membranes. J Memb Sci 199: 191-202.
Publication Dates
-
Publication in this collection
Apr-Jun 2018
History
-
Received
23 Mar 2017 -
Accepted
04 Oct 2017