Critical analyses when modeling tree biomass to ensure additivity of its components

ABSTRACT

It is presented the theme additivity of biomass of tree components. To evaluate and discuss this context, experimental information collected in forests of Acacia mearnsii De Wild. was used. Equations for components (stem and crown) and total biomass were fitted by means of two procedures: 1) generalized nonlinear least squares and 2) weighted-nonlinear seemingly unrelated regressions. Analyzing the performance of the estimators, it can be concluded that the two tested procedures are equivalent. On the other hand, this conclusion differs when evaluated the consistency and efficiency of the estimators. Fitting equations for the components and for the total biomass by an independent way is not realistic, because from a biological point of view the estimates of biomass are inconsistent, i.e., are not additive. The biomass estimates of the components and of the total, resulting from equations adjusted by means of systems of equations, provided narrower confidence intervals in relation to the equations adjusted independently, and is therefore more efficient. The second procedure presents better biological properties and statistics to estimate allometric equations for biomass of the components and for the total when compared with the independent estimation, thus it should be the method to be used.

Key words:
Biomass; Biological consistency; Non-linear regression; System of equations

1- INTRODUCTION

A basic premise must be considered when modeling biomass: the additivity. It means compatibility of biomass estimates of tree components (leaves, branches, bark, stem and root) with the tree total biomass. When modeling the tree biomass of components and its total, frequently fitting of the models are performed independently, i.e., it is done for each component without considering the interdependence existing between them. When using these equations, the sum of the components’ biomass will not result equal to the total biomass and thus is not biologically consistent. As Chiyenda and Kozak (1984) stated, it is unrealistic to consider that the components of the same tree are independent of each other.

In this sense, some assumptions need to be stated to ensure accuracy in the prediction of forest biomass on a large scale. Genet et al. (2011) state that a good set of equations for this purpose should meet the following characteristics: i) consistency - referring to the separation of the total biomass of a tree in standard components, ensuring, however, its additivity, ii) robustness - referring to the composition of an operating system that works correctly for wide variations in the sample population and with low sensitivity to the sampling procedure and the assumptions made and (iii) accuracy.

In this research, only the characteristics i and iii will be treated; robustness will not be included in its scope, because this is a more generic topic, important in large-scale inventories. For these purposes, when adjusting biomass equations for the total and for the components, three fundamental aspects are highlighted: performance of the equations, biological consistency of the equations and efficiency of the equation estimators. The performance refers to the quality of the estimates of biomass, while the biological consistency refers to the additivity of components with the total biomass. Regarding the efficiency of the estimators, we analyze the equations tested and choose the one that results in a smaller variance, which determines narrower confidence intervals for the dependent variables and, therefore, is more efficient.

Taking the best equations, evaluated through their performance, two important properties remain in modeling components’ biomass, because it is not satisfactory that only biomass equations are additive, but the estimator of the equations may be less efficient, or vice-versa. These issues have been researched over the past 50 years, highlighting the pioneering spirit of the researchers Kozak (1970), Cunia (1979), Jacobs and Cunia (1980), Chiyenda and Kozak (1984), Cunia and Briggs (1984, 1985) and Reed and Green (1985), which presented methods to achieve the additivity of the equations of biomass and, additionally, the review and dissemination of these procedures by Parresol (1999, 2001). Nevertheless, Nord-Larsen et al. (2017) observed that estimating model parameters using simultaneous estimation (NSUR) increased model bias compared with OLS estimation for most biomass components, i.e., contrary to the expectations that NSUR estimation always reduces the standard error of estimates, in certain restrictive conditions discussed by the authors.

Parresol (1999) has researched three procedures to ensure additivity of linear biomass’ equations and Parresol (2001) two procedures for equations that are not linear. In his research, he concluded that the procedure Seemingly Unrelated Regressions (SUR) for linear functions and Nonlinear Seemingly Unrelated Regressions (NSUR) for non-linear functions have resulted in more efficient estimators for components and total biomass, and the application of these procedures in component modeling is recommended. These works have provoked considerable influence in the dissemination of this type of modeling in various parts of the world, although in Brazil the application is restricted to studies conducted by Sanquetta et al. (2014, 2015). An alternative methodology has been presented by Dong et al. (2015), in which additivity is ensured by decomposing the component functions in a multiplicative manner, but it is difficult to work with this method, since it is difficult to constrain the component equation to show a logical behavior.

Some issues are worthy of attention because they justify the importance of the application of SUR and NSUR: (i) what is the gain in efficiency of these estimators over those obtained from a single equation? (ii) do the estimators of single equations produce biologically consistent estimates? (iii) are the estimates of biomass from the system of equations equivalent to those produced by equations estimated independently? (iv) are the estimated parameters and the statistics used to evaluate their quality of fit similar for systems of equations and for independently adjusted equations?

These issues have led to the presentation of this work and compose the following hypotheses, which were tested by means of conducting an experiment in black wattle forests (Acacia mearnsii De Wild.), in the state of Rio Grande do Sul, Brazil:

• i) “Considering that the equations obtained by means of fitting of single equation and of systems of equations are consistent statistically (without bias), then the estimates of biomass and the statistics of the fitted equations (coefficient of determination and coefficient of variation) obtained through these procedures do not differ among themselves”.

• (ii) “Given that the estimators for individual equations do not include restrictions to their coefficients, their estimates will not result in additivity of the components leading to biological inconsistency”.

• (iii) “Given that the estimator of systems of equations include contemporaneous correlations of components’ biomass in their fitting, the variance of biomass estimates are expected to be smaller when compared to the estimators obtained from a single equation and therefore should result in greater efficiency”.

Considering the assumptions made in this study, the objectives were to compare estimators of biomass through a single equation and by a system of equations, to evaluate their respective statistical estimates, their biological consistencies and, finally, their efficiencies.

2- MATERIALS AND METHODS

2.1- ORIGIN OF EXPERIMENTAL DATA

The field research was conducted during the months of June and July 2014 in forest stands of black wattle (Acacia mearnsii De Wild.), located in places that concentrate the plantations of this species in the state of Rio Grande do Sul, Brazil. We decided to divide these places in three regions: Municipality of Crystal, Encruzilhada do Sul and Piratini. These regions are characterized according to climate, type of relief and soil in Mochiutti (2007).

In each region four forest areas were sampled in a sequence of ages after planting, so as to cover all the rotation period of the culture (10 years). In Cristal, forest stands of 1.75, 2.75, 5.00 and 10.08 years old were sampled, in Encruzilhada do Sul of 1.83; 3.08; 5.75 and 10.75 years old and in Piratini 1; 2.33; 5.25 and 9.83 years old.

In a random manner, four circular plots with diameter of 22.56 m (400 m²) were allocated in each forest stand and in the center of each one also a subplot of 10 m in diameter (78.54 m²). This procedure was performed because it would not be possible to measure the variables of all trees in the plots, due to the high cost. Thus, it was decided to allocate a smaller sub-plot within the plot, in order to make feasible the proposed evaluations without affecting the research objectives.

The variables diameter at breast height and total height were measured in the plots. Yet, all trees inside each plot were felled and measured for the following characteristics: diameter at breast height, total height, and stem and crown biomass.

Thus, the present study encompassed the allocation of 48 plots, measurement of 3,462 pairs of diameter at breast height and total height and 670 trees for obtaining stem, crown and total biomass (defined as the sum of the stem and crown biomass) .

2.1.1- Measurement of variables in the plot

The goal of measuring the variables in the plot was to obtain the number of living trees per hectare. The values of the pairs of diameter at breast height and total height aimed to quantify, by means of equations, the biomass stocks of components per hectare.

The diameter at breast height (d) was measured using a dendrometric tape and the total height (h) a hypsometer (Haglöf). Forked trees below diameter at breast height were considered individual trees.

2.1.2- Measurement of variables in the sub-plot

All trees within the sub-plot were felled and assessed for the following characteristics:

• a) The diameter at breast height was measured using a dendrometric tape and the total height a measuring tape;

• b) The measurement of biomass was performed for the stem component (wood of the stem + bark) and for the crown (live and dead branches, leaves, flowers and fruits), taking the concepts defined in Picard et al. (2012). For each tree, these components were separated and weighed to assess the wet biomass using a digital scale (Portable Electronic Scale) with 5 g of precision;

• c) The dry crown and stem biomass were obtained from samples and immediately taken their masses using a digital scale (Hoyle) with a 1 g of precision. The crown samples weighted approximately 1,500 g and were taken along the crown of the tree at positions 0%, 25%, 50%, 75% and 95% in relation to the crown total length (away from the first branch, regardless of being alive or dead, to the crown apex). For the stem, 5 discs of 2 centimeters thick in the positions: 0%, 25%, 50%, 75% and 95% of the total height were removed;

• d) The samples were dried in an oven with movement and renewal of air at 100°C, and after constant mass, obtained through successive evaluations; the material was weighed in a digital scale with 1 g of precision. The dry biomass was obtained in [1].

$B_m=\frac{M{U}_{mi}M{S}_{mi}}{MU{A}_{mi}}$ (1)

Where: _^Bm = dry biomass of the _^mth component for stem or crown, in kg, for _^tth observation; _^MUmi = fresh mass of _^mth the component for stem or crown, in kg, for _^tth observation; _^MSi = dry mass of the sample of the _^mth component for stem or crown, in kg, for _^tth observation;_^MUAi = fresh mass of the sample of the _^mth component for the stem or crown, in kg, for _^tth observation.

2.2- EQUATIONS FOR ABOVE-GROUND BIOMASS

The equations for above-ground biomass of the components and for the total have been proposed considering the age of the forest stands, as is shown in Table I. We used the title group of equations for those that were independently estimated and system of equations for those jointly estimated. The qualitative classification of the stand age was proposed by the authors.

TABLE I
Group and systems of equations applied in stands of black wattle, in the state of Rio Grande do Sul, Brazil.

A group of equations / The system of equations	Stand age (years)	Stand age (Qualitative)
1	1	Too Young	69
2	1.75 - 1.83	Young	115
3	2.33 - 3.08	Inicial-mean-age	163
4	5 - 5.75	Advanced-Mean-age	153
5	9.83 - 10.75	Mature	170

• Where: T = number of sampled trees.

2.2.1- Biomass equations with independent estimates - Procedure 1

The models of Schumacher and Hall (1933) and Spurr (1952) were selected to express the allometry for the component biomass and for the total, as a function of the variables d and h. The models were fitted using estimated generalized nonlinear least squares, with definition of the estimators presented in Greene (2008). The resulting equations are presented in [2] to [16]. The White’s test (1980) was applied to test the hypothesis of homogeneity of residues in each equation, at 95% probability. For those cases in which the hypothesis was rejected, weights were obtained through the structure of the variances (results not shown), as defined in Harvey (1976) and Parresol (2001), followed by the new fitting of the equation and application of the White’s test.

R ¯ 2 CV White Group 1 ŷC=0.215867 (d2 h)0.445297 69.22% 22.11% 3.03ns (2) ŷs=0.178804 (d2 h)0.500678 83.98% 16.13% 10.01ns (3) ŷTotal=0.394430 (d2 h)0.471904 81.19% 16.86% 2.05ns (4) Group 2 ŷC=0.0328047 (d2 h)0.826434 64.07% 31.51% 1.71ns (5) ŷs=0.051673 (d2 h)0.839463 92.94% 12.45% 13.02ns (6) ŷTotal=0.086821 (d2 h)0.830291 89.28% 15.27% 4.84ns (7) Group 3 ŷC=0.003410 (d2 h)1.077143 89.80% 24.86% 1.38ns (8) ŷs=0.039333 (d2 h)0.900797 95.24% 13.39% 6.86ns (9) ŷTotal=0.037582 (d2 h)0.944718 95.94% 12.99% 1.67ns (10) Group 4 ŷC=0.005891 (d2 h)0.976956 80.70% 29.58% 6.97ns (11) ŷs=0.048390 d2.033388 h0.667959 95.19% 13.34% 6.69ns (12) ŷTotal=0.062245 d2.102267 h0.591272 95.43% 13.58% 6.04ns (13) Group 5 ŷC=0.000778 (d2 h)1.214249 82.89% 38.42% 4.67ns (14) ŷs=0.039145 d1.984245 h0.829223 95.73% 13.41% 8.58ns (15) ŷTotal=0.057760 d2.139698 h0.611213 95.95% 13.75% 4.84ns (16)

		${\overline{R}}^2$	CV	White
Group 1
ŷC=0.215867 (d2 h)0.445297		69.22%	22.11%	3.03ns	(2)
ŷs=0.178804 (d2 h)0.500678		83.98%	16.13%	10.01ns	(3)
ŷTotal=0.394430 (d2 h)0.471904		81.19%	16.86%	2.05ns	(4)
Group 2
ŷC=0.0328047 (d2 h)0.826434		64.07%	31.51%	1.71ns	(5)
ŷs=0.051673 (d2 h)0.839463		92.94%	12.45%	13.02ns	(6)
ŷTotal=0.086821 (d2 h)0.830291		89.28%	15.27%	4.84ns	(7)
Group 3
ŷC=0.003410 (d2 h)1.077143		89.80%	24.86%	1.38ns	(8)
ŷs=0.039333 (d2 h)0.900797		95.24%	13.39%	6.86ns	(9)
ŷTotal=0.037582 (d2 h)0.944718		95.94%	12.99%	1.67ns	(10)
Group 4
ŷC=0.005891 (d2 h)0.976956		80.70%	29.58%	6.97ns	(11)
ŷs=0.048390 d2.033388 h0.667959		95.19%	13.34%	6.69ns	(12)
ŷTotal=0.062245 d2.102267 h0.591272		95.43%	13.58%	6.04ns	(13)
Group 5
ŷC=0.000778 (d2 h)1.214249		82.89%	38.42%	4.67ns	(14)
ŷs=0.039145 d1.984245 h0.829223		95.73%	13.41%	8.58ns	(15)
ŷTotal=0.057760 d2.139698 h0.611213		95.95%	13.75%	4.84ns	(16)

2.2.2- Systems of Equations of biomass - Procedure 2

We used the model nonlinear seemingly unrelated regressions to fit the system of equations for the components and total biomass, with definitions of estimators in Srivastava and Giles (1987), Fiebig (2001), Greene (2008) and Parresol (2001). The White’s test (1980) was applied to test the hypothesis of homogeneity of the residuals for the equations of the components and for the total, at 95% probability. For those cases in which the hypothesis was rejected, the weights obtained in section 2.2.1 were used and the system was again fitted by means of the estimator weighted-nonlinear seemingly unrelated regressions. The fitted equations are presented in [17] to [31].

R ¯ 2 CV White System 1 ŷC=0.205422 (d2 h)0.459328 69.58% 21.98% 2.57ns (17) ŷs=0.17493 (d2 h)0.506569 84.19% 16.03% 9.63ns (18) ŷTotal= 0.205422 (d2 h)0.459328+ 0.17493 (d2 h)0.506569 81.15% 16.88% 1.65ns (19) System 2 ŷC=0.032844 (d2 h)0.827296 64.37% 31.38% 1.77ns (20) ŷs=0.052046 (d2 h)0.837992 92.99% 12.41% 11.93ns (21) ŷTotal=0.032844 (d2 h)0.827296+ 0.052046 (d2 h)0.837992 89.29% 15.26% 4.78ns (22) System 3 ŷC=0.003320 (d2 h)1.079325 89.84% 24.81% 1.28ns (23) ŷs=0.039548 (d2 h)0.899084 95.31% 13.30% 6.06ns (24) ŷTotal= 0.003320 (d2 h)1.079325+ 0.039548 (d2 h)0.899084 95.97% 12.95% 1.62ns (25) System 4 ŷC=0.004438 (d2 h)1.010899 80.58% 29.67% 6.33ns (26) ŷs=0.051517 d1.979083 h0.692747 95.24% 13.32% 6.21ns (27) ŷTotal= 0.004438 (d2 h)1.010899+ 0.051517 d1.979083 h0.692747 95.38% 13.15% 12.11ns (28) System 5 ŷC=0.001216 (d2 h)1.165186 82.39% 38.98% 5.37ns (29) ŷs=0.053628 d1.967389 h0.736520 95.84% 13.24% 6.63ns (30) ŷTotal= 0.001216 (d2 h)1.165186+ 0.053628 d1.967389 h0.736520 95.86% 13.89% 9.15ns (31)

		${\overline{R}}^2$	CV	White
System 1
ŷC=0.205422 (d2 h)0.459328		69.58%	21.98%	2.57ns	(17)
ŷs=0.17493 (d2 h)0.506569		84.19%	16.03%	9.63ns	(18)
ŷTotal= 0.205422 (d2 h)0.459328+ 0.17493 (d2 h)0.506569		81.15%	16.88%	1.65ns	(19)
System 2
ŷC=0.032844 (d2 h)0.827296		64.37%	31.38%	1.77ns	(20)
ŷs=0.052046 (d2 h)0.837992		92.99%	12.41%	11.93ns	(21)
ŷTotal=0.032844 (d2 h)0.827296+ 0.052046 (d2 h)0.837992		89.29%	15.26%	4.78ns	(22)
System 3
ŷC=0.003320 (d2 h)1.079325		89.84%	24.81%	1.28ns	(23)
ŷs=0.039548 (d2 h)0.899084		95.31%	13.30%	6.06ns	(24)
ŷTotal= 0.003320 (d2 h)1.079325+ 0.039548 (d2 h)0.899084		95.97%	12.95%	1.62ns	(25)
System 4
ŷC=0.004438 (d2 h)1.010899		80.58%	29.67%	6.33ns	(26)
ŷs=0.051517 d1.979083 h0.692747		95.24%	13.32%	6.21ns	(27)
ŷTotal= 0.004438 (d2 h)1.010899+ 0.051517 d1.979083 h0.692747		95.38%	13.15%	12.11ns	(28)
System 5
ŷC=0.001216 (d2 h)1.165186		82.39%	38.98%	5.37ns	(29)
ŷs=0.053628 d1.967389 h0.736520		95.84%	13.24%	6.63ns	(30)
ŷTotal= 0.001216 (d2 h)1.165186+ 0.053628 d1.967389 h0.736520		95.86%	13.89%	9.15ns	(31)

2.3- PERFORMANCE, CONSISTENCY AND EFFICIENCY OF THE ESTIMATORS OF THE BIOMASS EQUATIONS

The performance of the equations for total biomass and for the components obtained in procedure 1, in 2.2.1 and in procedure 2, in 2.2.2 were compared using the values of the coefficients of determination, the coefficients of variation and the coefficients of the estimated equations. Additionally, estimates of biomass for the components and for the total were obtained, using the data from the plots, at the tree level and per hectare. These estimates were compared by means of a Chi-square test, whose null hypothesis assumed that the values estimated by means of the procedure 1 are equal to those estimated by the procedure 2, at 95% probability.

The biological consistency was assessed in relation to the additivity of the biomass of the components to the total, only tested for the equations fitted by means of procedure 1. Taking the expression in [32], estimates of biomass were considered with biological consistency if ${\widehat{y}}_{Total}={\widehat{y}}_s+{\widehat{y}}_C$. If this condition is not satisfied, i.e., ${\widehat{y}}_s+{\widehat{y}}_C-{\widehat{y}}_{Total}\ne 0$, then the estimates of biomass were considered without biological consistency, and it was evaluated at tree and plot levels, and per hectare.

$\begin{array}{l}{y}_1=f_1\left(x_1,{\beta }_1\right)+{\epsilon }_1\\ y_2=f_2\left(x_2,{\beta }_2\right)+{\epsilon }_2\\ ⋮\\ y_k=f_k\left(x_k,{\beta }_k\right)+{\epsilon }_k\\ y_{total}=y_1+y_2+\dots +y_k+{\epsilon }_{total}\end{array}$ (32)

The efficiency of the estimators of the biomass equations fitted by means of procedures 1 and 2 was assessed in relation to the precision of confidence intervals in [33]. The confidence intervals were calculated for all the trees from the plots, using the formulations presented in Parresol (2001).

$PI{C}_i=\frac{I{C}_i}{{\widehat{y}}_i}$ (33)

Where:_^PICi = the precision of the confidence interval for the _^tth observation of the _^ith component; _^ICi = the confidence interval for the _^tth observation of the _^ith component; ŷ_i = the estimated value for the _^tth observation of the predictor variables.

The confidence intervals for ENGLS were calculated according to Greene (2008) and for WNSUR as presented in Parresol (2001).

3- RESULTS

3.1- PERFORMANCE OF THE ESTIMATORS OF BIOMASS EQUATIONS

The first hypothesis outlined in this paper: “considering that the equations obtained by means of the adjustment of single equation and of systems of equations are consistent statistically (without bias), then the estimates of biomass and the statistics of fitting of the equations (coefficient of determination and coefficient of variation) obtained through these procedures do not differ among themselves”, was confirmed as stated in the following paragraphs.

The values of the coefficients of the equations for the components’ biomass estimated by the procedure 1 $\left({\widehat{\beta }}_i\right)$ and through the procedure 2 $\left({\widehat{\beta }}_{ij}\right)$ showed similar trends in behavior in relation to the group or system of equations, although differences in the values of the coefficients has occurred. The largest differences - D were originated in the coefficients expressing the intercept of the equations $\left({\widehat{\beta }}_1\text{e}{\widehat{\beta }}_{i1}\right)$, which ranged from -56.30% to 24.66%. The other coefficients - $\left({\widehat{\beta }}_2\text{e}{\widehat{\beta }}_{i2}\right)$ and $\left({\widehat{\beta }}_3\text{e}{\widehat{\beta }}_{i3}\right)$ ranged between -3.71% to 11.18%.

The statistics for the assessment of the fitting quality, ${\overline{R}}^2$ and CV, for the biomass equations of the components and total, fitted by means of the procedure 1 and 2, showed similar trends in behavior in relation to the group or system of equations, and also with similar values. The differences for ${\overline{R}}^2$ ranged from -0.52% and 0.60%, whereas for CV between -1.46% and 3.17%. Still, by means of a graph to express the tendency among the observed values and estimated by procedures 1 and 2, were not observed deviations in relation to the estimated and observed values.

The estimates obtained through procedures 1 and 2 were compared by means of a Chi-square test and the obtained values were not significant, i.e., values were estimated by equations fitted by means of procedure 1 were similar to those estimated by equations fitted by means of procedure 2.

3.2- BIOLOGICAL CONSISTENCY OF THE BIOMASS EQUATIONS

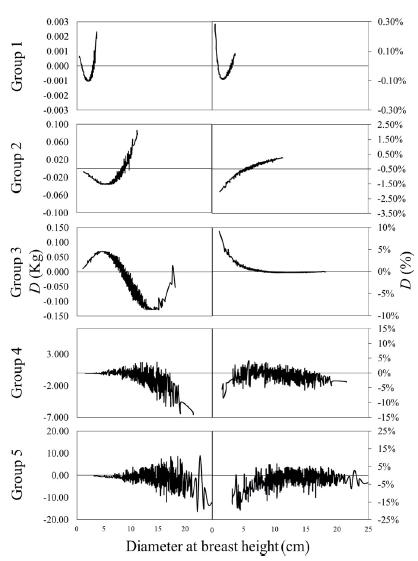
The restriction of biological consistency, i.e., ${\widehat{y}}_{Total}={\widehat{y}}_s+{\widehat{y}}_C$, was not observed logically, only for the equations of biomass of the components and for the total fitted by means of procedure 1. Therefore, being ${\widehat{y}}_s+{\widehat{y}}_C-{\widehat{y}}_{Total}\ne 0$, these equations were considered without biological consistency. The non-additivity of these equations (NA) at tree level is shown in Figure 1 for the variable d, when variations between -19.47% to 9.19% were observed.

Figure 1
Variation of non-additivity, i.e., discrepancy (D) of estimates of biomass components in relation to the total biomass, derived from equations adjusted by means of procedure 1, at tree level, observed in forest stands of black wattle species in the state of Rio Grande do Sul. Where: $D_i={\widehat{y}}_{s_i}+{\widehat{y}}_{C_i}-{\widehat{y}}_{Tota{l}_i}$ in kg, or $D_i=\frac{\left({\widehat{y}}_{s_i}+{\widehat{y}}_{C_i}-{\widehat{y}}_{Tota{l}_i}\right)}{\left({\widehat{y}}_{s_i}+{\widehat{y}}_{C_i}\right)}100$ in percentage, and i is the _^ith observation of the group of equations.

The biological inconsistency was also observed at plot level, in which the non-additivity of the equations ranged between -4.09% to 2.22%. In the same way, was observed per hectare, with variations between -0.97% and 0.05% (Figure 2).

Figure 2
Non-additivity $\left(NA\right)$ of biomass estimates of the components in relation to the total from equations fitted by means of procedure 1, at plot level and per hectare. Where: the calculation for the plot is given by $N{A}_i={\widehat{y}}_{s_i}+{\widehat{y}}_{C_i}-{\widehat{y}}_{Tota{l}_i}$ in t.ha^-1, and related to the _^ith plot of the group of equations, and per hectare as $NA={\widehat{y}}_s+{\widehat{y}}_C-{\widehat{y}}_{Total}$, in t.ha^-1.

Therefore, the second hypothesis outlined in this paper - “since the estimators of systems of equations present restrictions to obtain the coefficients in their settings, their estimates should result in additivity of components, when compared with the estimators obtained by a single equation, and, consequently, result in biological consistency” - has been proven.

3.3- EFFICIENCY OF THE ESTIMATORS OF THE EQUATIONS OF BIOMASS

The precision of the estimates, using the equations fitted by means of procedure 1, for the crown component ranged from 5.46% to 41.11%, for the stem component from 2.12% to 21.30% and for the total from 1.29% to 21.74%. For the equations fitted by means of procedure 2, the specifications for the crown component vary between 0.75% to 28.24%, for the stem component from 1.62% to 20.43% and for the total from 0.28% to 20.62%.

The estimates of biomass for the components and for the total, using the equations fitted by means of procedure 2, resulted in narrower confidence intervals, therefore more efficient. The efficiencies in the confidence intervals between (EIC) varied from 5.39% to 77.04% (Figure 3), depending on the component and the system of equations. On average, in general, EIC were higher for the crown biomass component, followed by the total and by the stem components, respectively of 51.64%, 27.79% and 15.98%.

Figure 3
Efficiency in the confidence interval (EIC) for estimates of biomass for the components and for the total from equations fitted by procedure 2. Where: $EI{C}_i=1-\frac{PI{C}_{WNSU{R}_i}}{PI{C}_{ENGL{S}_i}}100$, in percentage, and _^PICWNSUR the average of accuracy of the confidence interval for the _^ith component, obtained for equations adjusted by means of procedure 1 and _^PICENGLS the average of accuracy of the confidence interval for the _^ith component obtained for equations fitted by means of procedure 1.

Thus, the third hypothesis outlined in this paper - “since the estimators of systems of equations include the contemporaneous correlations of the biomass components in their fittings, their estimates should result in a smaller variance, when compared with the estimators obtained by single equation, and, consequently, result in greater efficiency” - has been proven.

4- DISCUSSION

4.1- PERFORMANCE OF THE ESTIMATORS OF THE BIOMASS EQUATIONS

The statistics for the assessment of the fitting quality, ${\overline{R}}^2$ and CV, were similar in relation to the method of fitting the equations. Some of the statistics obtained from the equations fitted by procedure 2 led to a slight improvement and others did not. This is a direct effect of the flexibility of the estimator to meet the requirement of additivity of the components, and it has also been observed by Reed and Green (1985). Even if it occurs, does not affect the predictions, since the estimates of the components’ biomass and of the total obtained by the systems or groups of equations, did not differ among themselves, as proven by the Chi-square test.

The systems and groups of Equations 1, 2 and 3 were defined by the same regressors to the functions of the components and this resulted in similar values for the obtained coefficients. This is a special case, in which the estimates of the coefficients, by means of the system of equations or individually, are equivalent. Greene (2008) demonstrated this condition in a comparative approach of the generalized least squares estimator (equivalent to the Seemingly Unrelated Regressions) with ordinary least squares (equivalent to the equations fitted independently). In this condition, assuming that_^Xi=Xj=X , then, $X_i^{\text{'}}{X}_J=X^{\prime }X$ to all i and j on [34].

$\widehat{\beta }={\left(X^{\prime }{\Omega }^{-1}X\right)}^{-1}{X}^{\prime }{\Omega }^{-1}y={\left[X^{\prime }\left({\sum }^{-1}\otimes I\right)X\right]}^{-1}{X}^{\prime }\left({\sum }^{-1}\otimes I\right)y$ (34)

The inverse of the matrix on the right side becomes, therefore, ${\left({\sum }^{-1}\otimes X^{\prime }X\right)}^{-1}$. Using the product properties of Kronecker, in which ${\left(A\otimes B\right)}^{-1}=\left(A^{-1}\otimes B^{-1}\right)$, being A of size K∙L and B of m∙n, ${\left({\sum }^{-1}\otimes X^{\prime }X\right)}^{-1}$ is equivalent to ${\left({\sum }^{-1}\otimes X^{\prime }X\right)}^{-1}$. Still, on the right side of the expression in [34], each term $X_i^{\text{'}}{y}_j$ is equivalent to _^X’yi , which in turn is equivalent to _^X’Xbj . With these results, after the elimination of the common values of X’X, the estimate of β is defined in [35].

$\widehat{\beta }=\left[\begin{array}{cccc}{\sigma }_{11}{\left(X^{\prime }X\right)}^{-1}& {\sigma }_{12}{\left(X^{\prime }X\right)}^{-1}& \cdots & {\sigma }_{1M}{\left(X^{\prime }X\right)}^{-1}\\ {\sigma }_{21}{\left(X^{\prime }X\right)}^{-1}& {\sigma }_{22}{\left(X^{\prime }X\right)}^{-1}& \cdots & {\sigma }_{2M}{\left(X^{\prime }X\right)}^{-1}\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{M1}{\left(X^{\prime }X\right)}^{-1}& {\sigma }_{M2}{\left(X^{\prime }X\right)}^{-1}& \cdots & {\sigma }_{MM}{\left(X^{\prime }X\right)}^{-1}\end{array}\right]\left[\begin{array}{c}\left(X^{\prime }X\right){\displaystyle \sum }_{l=1}^M{\sigma }_{1l}{b}_l\\ \left(X^{\prime }X\right){\displaystyle \sum }_{l=1}^M{\sigma }_{2l}{b}_l\\ ⋮\\ \left(X^{\prime }X\right){\displaystyle \sum }_{l=1}^M{\sigma }_{Ml}{b}_l\end{array}\right]$ (35)

Taking the first sub-vector to estimate β, after multiplication and cancellation of the momentum matrix is defined in [36].

${\widehat{\beta }}_1={\displaystyle \sum }_{j=1}^M{\sigma }_{1j}{\displaystyle \sum }_{l=1}^M{\sigma }_{jl}{b}_l=b_1\left({\displaystyle \sum }_{j=1}^M{\sigma }_{1j}{\sigma }_{j1}\right)+b_2\left({\displaystyle \sum }_{j=1}^M{\sigma }_{1j}{\sigma }_{j2}\right)+\dots +b_M\left({\displaystyle \sum }_{j=1}^M{\sigma }_{1j}{\sigma }_{jM}\right)$ (36)

The terms in parentheses are elements of the first line of ∑∑^-1=I, so the final result corresponds to ${\widehat{\beta }}_1=b_1$, i.e. ${\widehat{\beta }}_i=b_i$, what would determine that the more efficient estimator would be the single equation. However, in some special cases, as the modeling of biomass components, results are compromised, since there are restrictions on β, which can be inside of the equations or between the equations. Such guidance indicates that, given the condition of the equations are composed by the same regressors, and due to restrictions that are imposed on the coefficients of the equations of the components to be additive, the coefficients will tend to similarity, even if the gain in efficiency by the system of equations still prevail (as approach performed below).

Through the performance analysis of the estimators, particularly in relation to the estimates of biomass and the statistics of fitting the equations, it can be concluded that the two tested procedures 1 and 2 are equivalent. On the other hand, this conclusion differs when evaluated the consistency and efficiency of the estimators.

4.2- BIOLOGICAL CONSISTENCY OF THE BIOMASS EQUATIONS

Whereas the statistical consistency of the estimators becomes better as we increase the sampling intensity, this reality can also be improved through statistical and computer techniques for obtaining allometric relationships. In other words, this consistency becomes more enhanced the closer are the allometric estimators of the true population values. If statistical modeling can approximate estimators of real population values (which is provided by least squares estimators), and also ensure an additive system of the parts of the organism with its whole, they are therefore biologically consistent, hence the nomination of Biological Consistency.

The condition of biological consistency, ensured by the restriction that the biomass results of the components must be additive to match the result of the total biomass, was not satisfied for the equations fitted through procedure 1. The non-additivity (NA) was observed at tree level, at plot level, assuming positive and negative values, and also per hectare. After several approaches taken in the past 50 years: Kozak (1970), Jacobs and Cunia (1980), Chiyenda and Kozak (1984), Cunia and Briggs (1984, 1985), Reed and Green (1985). Parresol (1999, 2001), Návar et al. (2002), Carvalho and Parresol (2003), Bi et al. (2004, 2010, 2015), Lambert et al. (2005), Brandeis et al. (2006), António et al. (2007), Návar (2009), Menéndez-Miguélez et al. (2013), Li and Zhao (2013), Dong et al. (2014, 2015), Sanquetta et al. (2014, 2015), MacFarlane (2015), Tesfaye et al. (2015), Zhao et al. (2015), Zheng et al. (2015), Affleck and Diéguez-Aranda (2016), Poudel and Temesgen (2016), emphasize the importance of establishing additive equations of biomass. The lack of additivity is an undesirable property because it propagates the biological inconsistency from the tree level to the estimates for the forest as a whole, affecting estimates in forest biomass inventories.

The biological inconsistency, in percentage terms, was higher at tree level. In this condition, positive and negative NA values do not cancel out, resulting in relative greater inconsistency than when compared at plot level, or per hectare. There were no trends established for the lack of additivity concerning the independent variables.

The biological inconsistency in absolute or relative terms, at tree level, was higher in groups of equations 4 and 5, i.e., in older forest stands, and relates to the composition of the models for components’ biomass and total. The proposed models for components’ biomass and total for the groups of Equations 1, 2 and 3 were the same, for groups of equations 4 and 5 the models proposed for crown and stem biomass were different. The lack of additivity was not even higher, because the used model for the total biomass was the same as for the stem.

The non-additivity was lower in percentage terms at plot level. In this case, the biomass of a component or for the total $({\widehat{y}}_i)$ for the _^hth plot corresponds to the sum of biomass estimated for _^tth trees. Thus, when adding the total numbers of sampled trees, positive and negative values that can generate NA at the tree level cancel out. This convergence does not tend to zero, due to the combination of the probabilistic distribution of independent variables in the plot with the randomness of NA at tree level.

In the same way, this also occurs when taking the average values of the plots to compose the biomass estimator per hectare. For this condition, the biological inconsistency for the 5 groups of equations ranged from -0.05% to -0.97%, is equivalent -0.001 to -1.31 _^t.ha-1 . Although the biological inconsistency decreases as the estimators of biomass are calculated in _^t.ha-1 , still remains and becomes significant when the estimator is extrapolated to the entire area of the forest stand. In addition, it is more severe when the inventories of biomass are done in large areas, for example, in the inventories of biomass at regional, state and national levels.

The equations adjusted independently generate biological inconsistent results, which implies that models for components’ biomass and for the total should be estimated by means of systems of equations. Most of the equations used for the species black watlle, as well as for other species in Brazilian forests, were fitted independently. Therefore, these equations do not reach biological consistency and, consequently, we must take certain precautions before we simply use them.

An alternative to take advantage of the hundreds of equations of biomass, that were applied without considering the additivity principle, is to set for the total biomass the sum of the masses of the components. In this case, as it is also of interest to know the variance of the total biomass $\left({\sigma }_{y_{Total}}^2\right)$ to establish confidence intervals, it can be obtained as a function of the variances and covariances of estimates of the components. The values of the variance tend to be larger, because they are dependent on the variances of each component $\left({\sigma }_{y_i}^2\right)$ and on the covariances between the estimates $\left(cov\left(y_i,y_j\right)\right)$, as defined in [37]. This approach is presented in Parresol (1999, 2001) and Sanquetta et al. (2015), and it is recommended that it be applied to non-additive biomass equations.

${\sigma }_{y_{Total}}^2={\displaystyle \sum }_{i=1}^k{\sigma }_{y_i}^2+2\sum \sum cov\left(y_i,y_j\right)$ (37)

4.3- EFFICIENCY OF THE ESTIMATORS OF THE BIOMASS EQUATIONS

Hypothetically, having been solved the biological inconsistency of the independently estimated equations (using the references already cited), and knowing the slight difference in performance between the independent estimators and of systems of equations for the components, it could be concluded once more on the non-difference of the equations fitted logically by means of procedures 1 and 2. However, in a third analysis, which considers the efficiency of the estimators, i.e., by a process which results in the minimum variance, the equations fitted by means of procedure 2 are more efficient. This superiority, both for components’ biomass as well as for total biomass, it is undeniable, since they will produce estimates with smaller variance, i.e., with narrower confidence intervals, by considering the correlation that exists between the components of the tree. As highlight by Zellner (1962) and Zellner and Huang (1962), the gain in efficiency occurs when the terms of the disturbances of different equations are correlated. Therefore, it is likely that this always happens when it comes to the tree biomass.

For the systems of equations adjusted by procedure 2, the contemporaneous correlation matrices were presented (Systems S1-S5 - Supplementary Material). Through them it was possible to demonstrate the correlations that occur between the measured components on the same tree, i.e., the dependence between the components of biomass. These correlations are the ones that will determine the efficiency gains due to the application of seemingly unrelated regressions.

Chiyenda and Kozak (1984) emphasize that it is unrealistic to consider that the tree components are independent, or that the residuals ${\epsilon }_i=\mathrm{1,}\dots ,k$ of components are not correlated, since the same tree is composed of information for more than one component of biomass. When considering these correlations, the equations adjusted through procedure 2 will provide estimates with smaller variance, that is, the result that determines the higher efficiency of the estimator. Thus, if a particular estimate of biomass results in smaller variance, hence its confidence interval is also narrower and, therefore, the estimate is more accurate. In addition, the existence of contemporaneous correlations makes it possible to obtain the best unbiased estimators for the equations of the components and for the total. Therefore, it is reasonable to conclude that this estimator should be used to adjust biomass equations for the components and for the total.

The estimates of the components’ biomass and of the total resulting from equations fitted through procedure 2 made it possible to obtain narrower confidence intervals in relation to the equations adjusted through procedure 1, which was proved by means of the analysis of the obtained confidence intervals. This demonstrates that the most efficient strategy to adjust biomass by seemingly unrelated regressions. These perceptions are also conclusive in studies conducted by Parresol (1999, 2001), Sanquetta et al. (2015) and Zhao et al. (2015).

The values of the coefficients expressing the intercepts of the equations $\left({\widehat{\beta }}_1\text{e}{\widehat{\beta }}_{i1}\right)$ led to close relations with the fitting method, mainly in what refers to the standard errors of coefficients, since the equations adjusted by means of procedure 2 resulted in smaller standard errors when compared to those obtained by equations fitted by means of the procedure 1. This is a direct effect of the inclusion of correlations in procedure 2, which was clearly evidenced by Parresol (1999, 2001).

The efficiency provided by procedure 2 changed in the forests too young to mature. In young forest stands the contemporaneous correlation between biomass components was stronger, evidencing that in these ages the biomass distribution on the components is dependent on intrinsic factors of the species. In the older forest stands, the correlation between biomass components decreased, evidencing that the biomass allocation is dependent on external factors of the plant which affects its correlation. This is a consequence of the biological growth of plants, since the allocation of components’ biomass as a function of their age is changed, therefore determines different contemporaneous correlations and, consequently, different degrees of accuracy in the estimates. In this sense, an aspect which denotes special attention is that concerning the crown component.

By means of the contemporaneous correlation matrices it is observed that the crown correlations with the stem and total biomass, estimated in the same tree, decrease from the very young forest to the mature one. The opposite was observed for the stem in relation to the total biomass, reflecting the effect of the allocation of components’ biomass along the growth stages of the forest. Although the correlation of the crown component with the other components of the tree decreases over the years, it still has to be considered, since it will be an important element to make the estimates of this component more precise. By its nature, the crown is a difficult component to be modeled, so using an estimator that results in more accurate estimates is crucial, especially because this component gains importance in mature forests, since it is the raw material for energy production. These results confirm the importance of implementation of procedure 2.

4.4- IMPORTANCE OF ADDITIVE EQUATIONS AND SMALLER VARIANCE

In agreement with the analysis of the equations perfomance, the biological consistency and efficiency of the statistics, undoubtedly it is concluded that the equations fitted by means of procedure 2 are the ones that should be used, because they provide accurate estimates for the components’ biomass: crown biomass and total, with the main characteristic of being obtained with smaller variance.

The use of procedure 2 results in statistically correlated equations, which are definitively related through contemporaneous disturbances of the equations - which gives rise to the nomenclature: apparently unrelated equations. The inclusion of the contemporaneous correlations between the biomass of the components and total biomass in the fitting of the equation systems through this procedure resulted in narrower confidence intervals, thus showing one of its most important properties, efficiency. The equations adjusted by means of procedure 1 do not take into account the contemporaneous correlations, which impairs the efficiency of this estimator.

How much is this efficiency? This issue is worthy of attention because it is what justifies the importance of applying procedure 2. In this study, the efficiencies in the 95% confidence intervals (EIC) ranged from 5.39% to 77.04%, depending on the component and the system of equations, therefore an outcome that should be considered relevant. Zellner (1962), and Dwivedi and Srivastava (1978) analyzed this issue in detail, noting the conditions to be the gain in efficiency of the regression estimators is apparently not related in comparison to the average of single equation. The authors showed that the main condition for efficiency gain is due to the existence of a correlation between residuals of the equations, since, the stronger it is, greater is the gain in efficiency of the estimators of seemingly unrelated regressions, than when the average of a single equation is considered.

Another important property of systems of equations adjusted by means of procedure 2 is the additivity of the equations, desirable characteristic and fundamental in modeling tree biomass. The additivity of biomass estimates has been recommended by several researches: Kozak (1970), Chiyenda and Kozak (1984), Cunia and Briggs (1984), Paressol (1999, 2001), Carvalho and Parresol (2003), Sanquetta et al. (2015), Zhao et al. (2015) and Affleck and Diéguez-Aranda (2016). In this work, the additivity of the components to compose the total biomass was guaranteed using procedure 2 and, having been established a model for each biomass component, that for the total biomass was defined in relation to the variables that composed the functions of the components.

There are other specifications of models and methods of estimation to force the additivity of biomass components to compose the total biomass for linear and non-linear functions, according to approaches that were performed by Kozak (1970), Jacobs and Cunia (1980), Chiyenda and Kozak (1984), Cunia and Briggs (1984, 1985), Reed and Green (1985), Parresol (1999, 2001), Carvalho and Parresol (2003), Sanquetta et al. (2015). In this context, Parresol (2001) highlights: I almost unilaterally recommend the joint generalized least squares approach for both linear or nonlinear modeling of biomass equations systems. This is due to the following aspects:

• Once the components of biomass are not independent, they will be contemporaneously correlated;

• The apparently unrelated regression approach allows us to account for these correlations to establish equations with smaller variances;

• The intensity of the contemporaneous correlation is what determines the values of variance of equations. Thus, the larger this correlation is, the smaller will be the variance, therefore, the greater will be the gain in efficiency on the confidence intervals of the coefficients and of the estimates.

The structure of the models presented in procedure 2 was used to ensure the property of additivity for nonlinear models of biomass. The proposed system guaranteed additive equations and, by including the structure of the variance of the error in the fitting of functions, also minimized estimates of variance. The structure of the systems of equations presented is similar to that proposed by Parresol (2001). In this case, the estimates of the components’ biomass and total are assured by the following aspects:

• Each component is expressed by a function, considered the best through the process of choice of competitive models;

• The model for the total biomass is a function of the independent variables that compose the components, resulting in additivity;

• Each equation of biomass, for components or total, has its own weighted function, so as to ensure estimates with minimum variance.

In addition to the biomass additivity, it is important to ensure that the resulting functions have been adjusted for the condition that provides estimates of minimum variance. Experimentally, the heteroscedasticity of the residues in each of the biomass equations worsened as the forest became older. In fact, this result is not surprising, because in the mature forest condition the biomass deviations from their mean increase from the smaller to the larger classes. This allows to emphasize the importance of the correction of heteroscedasticity, given its effect on the estimates of the biomass equations.

To eliminate the heteroscedasticity of the residuals, a weighted function was established for each component of the biomass in order to model the structure of the variance os its residuals. By means of these functions, weights were calculated to stabilize the variance disturbances, whose conditions allowed the weighted estimator to generate equations with minimum variance and narrower confidence intervals. These results highlight the importance of conducting the modeling of the error structure, in order to ensure reliable estimates of each of the biomass components and also for the total with minimum variance.

Additivity and efficiency of biomass estimates of the components and total are prerequisites in the inventories of biomass. Thus, the approach presented in this work for the set of functions of biomass, by means of the procedure 2, proved to be appropriate, because of the following reasons:

• Performance: estimation of biomass and good fitness of the equation similar to the method that maximizes the quality of the equation fitted independently;

• Biological Consistency: the equations of biomass of the components are additive to compose the equation of total biomass;

• Statistical Efficiency: estimation of biomass and coefficients with smaller variance, therefore more efficient.

Through the estimates of equations, using procedure 2, it is possible to estimate systems of equations statistically correlated and, through the inclusion of correlations in the fitting, it was obtained equations with smaller variance, which propitiated to obtain more efficient estimates of the parameters and more reliable ranges for the estimates. The consideration of the additivity of systems of equations ensured the consistency of biological estimates of components’ biomass and the total.

Due to the smaller variance, the systems of equations adjusted by means of procedure 2 produced more accurate estimates, since the confidence intervals were narrower. This was also evidenced by Parresol (1999, 2001), who demonstrated the superiority of statistical efficiency and consistency of biological equations fitted by seemingly unrelated regressions, respectively for linear and non-linear functions. This allows an important application in estimates of biomass in forest inventories, since the errors from the equations should be considered in the calculation of the total sampling error, as shown by Cunia (1987).

Therefore, if the equations adjusted by means of procedure 2 result in smaller variance, it becomes acceptable that this minor error also propagate in the estimates per hectare, resulting in more accurate estimates when compared with the equations fitted by ENGLS. In this case, it is reinforced the importance of entering the structure of the error in the adjustment of the biomass equations in order to achieve efficient estimates and narrower confidence intervals. Therefore, these concepts reinforce the importance of using procedure 2 to establish biomass equations.

Parresol (2001) emphasizes that the additivity property ensures that regression functions be consistent one with another, since a component of the tree is part of the other component, therefore it is logical to expect that the estimates of the parties do not exceed the whole. This property has determined the consistency of the equations adjusted by means of procedure 2 for the reported examples, in which the total biomass above ground was divided into two components: stem biomass and crown biomass. According to Parresol (2001), this property can be applied to any quantity that is disaggregated in a logical system of components.

5- CONCLUSIONS

All assumptions made in this study were duly confirmed.

i) Performance of equations

The two procedures tested do not differ in relation to performance evaluation.

ii) Biological consistency of the equations

To estimate the equations of biomass independently for the components and for the total, is not realistic, i.e., are not additive.

A property in setting equations by means of the regression model apparently unrelated is the additivity, i.e., the estimates of the components’ biomass are added to form the total.

iii) Efficiency of the estimators of the equations

Equations estimated by the seemingly unrelated regression produce estimates with smaller variance. Therefore, from the statistical point of view they are more efficient when compared with the independent estimated equations.

Estimating the biomass equations of the components and total biomass separately, means disregarding their interdependencies, resulting in equations that will provide estimates with larger variance, therefore, less efficient.

iiii) Systems of equations

The apparently unrelated regression model presents better biological and statistical properties to estimate biomass allometric equations for components and total biomass when compared to independent estimation. Therefore, it is the method that should be used.

REFERENCES

• AFFLECK DLR AND DIÉGUEZ-ARANDA U. 2016. Additive nonlinear biomass equations: a likelihood-based approach. For Sci 62: 129-140.
• ANTÓNIO N, TOMÉ M, TOMÉ J, SOARES P AND FONTES L. 2007. Effect of tree, stand, and site variables on the allometry of Eucalyptus globulus tree biomass. Can J For Res 37: 895-906.
• BI H, LONG Y, TURNER J, LEI Y, SNOWDON P, LI Y, HARPER R, ZERIHUN A AND XIMENES F. 2010. Additive prediction of aboveground biomass for Pinus radiata (D. Don) plantations. For Ecol Manage 259: 2301-2314.
• BI H, MURPHY S, VOLKOVA L, WESTON C, FAIRMAN T, LI Y, LAW R, NORRIS J, LEI X AND CACCAMO G. 2015. Additive biomass equations based on complete weighing of sample trees for open eucalypt forest species in south-eastern Australia. For Ecol Manage 349: 106-121.
• BI H, TURNER J AND LAMBERT M. 2004. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 18: 467-479.
• BRANDEIS TJ, DELANEY M, PARRESOL BR AND ROYER L. 2006. Development of equations for predicting Puerto Rican subtropical dry forest biomass and volume. For Ecol Manage 233: 133-142.
• CARVALHO JP AND PARRESOL BR. 2003. Additivity in tree biomass components of Pyrenean oak (Quercus pyrenaica Willd.). For Ecol Manage 179: 269-276.
• CHIYENDA SS AND KOZAK A. 1984. Additivity of component biomass regression equations when the underlying model is linear. Can J For Res 14: 441-446.
• CUNIA T. 1979. On tree biomass tables and regression: some statistical comments. In: Frayern WE (Ed), Forest resource inventories. Workshop proceedings…., Colorado: Colorado State University, p. 629-642.
• CUNIA T. 1987. Error of forest inventory estimates: its main components. In: Wharton EH and Cunia T. Estimating tree biomass regressions and their error. Proceedings of the workshop on tree biomass regression functions and their contribution to the error of forest inventory estimates. USDA: For Serv Gen, USA, p. 1-13.
• CUNIA T AND BRIGGS RD. 1984. Forcing additivity of biomass tables-some empirical results. Can J For Res 14: 376-384.
• CUNIA T AND BRIGGS RD. 1985. Forcing additivity of biomass tables: use of the generalized least squares method. Can J For Res 15: 23-28.
• DONG L, ZHANG L AND LI F. 2014. A compatible system of biomass equations for three conifer species in Northeast, China. For Ecol Manage 329: 306-317.
• DONG L, ZHANG L AND LI F. 2015. A three-step proportional weighting system of nonlinear biomass equations. For Sci 61: 35-45.
• DWIVEDI TD AND SRIVASTAVA VK. 1978. Optimality of least squares in the seemingly unrelated regression equation model. J Econom 7: 391-395.
• FIEBIG DG. 2001. Seemingly Unrelated Regression. In: Baltagi B (Ed), A Companion to Theoretical Econometrics. Oxford: Backwell Publishers, United Kingdom, p. 101-121.
• GENET A ET AL. 2011. Ontogeny partly explains the apparent heterogeneity of published biomass equations for Fagus sylvatica in central Europe. For Ecol Manage 261: 1188-1202.
• GREENE WH. 2008. Econometric analysis. Upper Saddle River: Prentice-Hall, 1178 p.
• HARVEY AC. 1976. Estimating regression models with multiplicative heteroscedasticity. Econometrica 44: 461-465.
• JACOBS MW AND CUNIA T. 1980. Use of dummy variables to harmonize tree biomass tables. Can J For Res 10: 483-490.
• KOZAK A. 1970. Methods of ensuring additivity of biomass components by regression analysis. For Chron 46: 402-404.
• LAMBERT MC, UNG CH AND RAULIER F. 2005. Canadian national tree aboveground biomass equations. Can J For Res 35: 1996-2018.
• LI H AND ZHAO P. 2013. Improving the accuracy of tree-level aboveground biomass equations with height classification at a large regional scale. For Ecol Manage 289: 153-163.
• MACFARLANE DW. 2015. A generalized tree component biomass model derived from principles of variable allometry. For Ecol Manage 354: 43-55.
• MENÉNDEZ-MIGUÉLEZ M, CANGA E, BARRIO-ANTA M, MAJADA J AND ÁLVAREZ-ÁLVAREZ P. 2013. A three level system for estimating the biomass of Castanea sativa Mill. coppice stands in north-west Spain. For Ecol Manage 291: 417-426.
• MOCHIUTTI S. 2007. Produtividade e sustentabilidade de plantações de acácia-negra (Acacia mearnsii De Wild.) no Rio Grande do Sul. 270 f. Tese (Doutorado em Ciências Florestais) - Universidade Federal do Paraná. Curitiba.
• NÁVAR J. 2009. Biomass component equations for Latin American species and groups of species. Ann For Sci 66: 208.
• NÁVAR J, MÉNDEZ E AND DALE V. 2002. Estimating stand biomass in the Tamaulipan thornscrub of northeastern Mexico. Ann For Sci 59: 813-821.
• NORD-LARSEN T, MEILBY H AND SKOVSGAARD JP. 2017. Simultaneous estimation of biomass models for 13 tree species: effects of compatible additivity requirements. Can J For Res 47: 765-776.
• PARRESOL BR. 1999. Assessing tree and stand biomass: a review with examples and critical comparisons. For Sci 45: 573-593.
• PARRESOL BR. 2001. Additivity of nonlinear biomass equations. Can J For Res 31: 865-878.
• PICARD N, SAINT-ANDRÉ L AND HENRY M. 2012. Manual for building tree volume and biomass allometric equations: from field measurement to prediction. Rome e Montpellier: Food and Agricultural Organization of the Unites Nations and Centre de Coopération Internationale en Recherche Agronomique pour le Développement, 215 p.
• POUDEL KP AND TEMESGEN H. 2016. Methods for estimating aboveground biomass and its components for Douglas-fir and lodgepole pine trees. Can J For Res 46: 77-87.
• REED DD AND GREEN EJ. 1985. A method of forcing additivity of biomass tables when using nonlinear models. Can J For Res 15: 1184-1187.
• SANQUETTA CR, BEHLING A, CORTE AP, SIMON A, PSCHEIDT H, RUZZA MS AND MOCHIUTTI S. 2014. Estoques de biomassa e carbono em povoamentos de acácia negra em diferentes idades no Rio Grande do Sul. Sci For 42: 361-370.
• SANQUETTA CR, BEHLING A, CORTE APD, PÉLLICO NETTO S, SCHIKOWSKI AB AND AMARAL M. 2015. Simultaneous estimation as alternative to independent modeling of tree biomass. Ann For Sci 72: 1099-1112.
• SCHUMACHER FX AND HAL FS. 1933. Logarithmic expression of timber-tree volume. J Agric Res 47: 719-734.
• SPURR SH. 1952. Forest inventory. New York: The Ronald Press Company, 476 p.
• SRIVASTAVA VK AND GILES DEA. 1987. Seemingly Unrelated Regression Equations Models. Estimation and Inference. New York: Marcel Decker, 374 p.
• TESFAYE MA, BRAVO-OVIEDO A, BRAVO F AND RUIZ-PEINALDO R. 2015. Aboveground biomass equations for sustainable production of fuelwood in a native dry tropical afro-montane forest of Ethiopia. Ann For Sci 73: 411-423.
• WHITE H. 1980. A heteroskedasticity consistent covariance matrix estimator and a direct test of heteroskedasticity. Econometrica 48: 817-838.
• ZELLNER A. 1962. An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. J Am Stat Assoc 57: 348-368.
• ZELLNER A AND HUANG DS. 1962. Further properties of efficient estimators for seemingly unrelated regression equations. IER 3: 300- 313.
• ZHAO D, KANE M, MARKEWITZ D, TESKEY R AND CLUTTER M. 2015. Additive tree biomass equations for mid-rotation loblolly pine plantations. For Sci 61: 613-623.
• ZHENG C, MASON EG, JIA L, WEI S, SUN S AND DUAN J. 2015. A single-tree additive biomass model of Quercus variabilis Blume forest in North China. Trees 29: 705-716.

Publication Dates

• Publication in this collection
  17 May 2018
• Date of issue
  Apr-June 2018

History

• Received
  23 Oct 2017
• Accepted
  11 Dec 2017