Ground level photosynthetically active radiation dynamics in stands of Acacia mearnsii De Wild

ABSTRACT

The objective is to study the dynamics of photosynthetic radiation reaching the soil surface in stands of Acacia mearnsii De Wild and its influence on height growth in stands. This fact gives rise to the formulation of the following hypothesis for this study: "The reduction of the incidence of light inside the stand of black wattle will cause the inflection point in its height growth when this reaches 4 to 5 m in height, i.e. when the stand is between 2 and 3 years of age". The study was conducted in stands in the state of Rio Grande do Sul, Brazil, where diameters at breast height, total height and photosynthetically active radiation available at ground level were measured. The frequency tended to be more intense when the age of the stands increases. It was evident that a reduction of light incidence inside the forest occurred, caused by canopy closure. Consequently, closed canopy propitiated the competition of plants. This has affected the conditions for growth in diameter and height of this species, reason why it becomes possible to conceive the occurrence of an inflection point in the growth of these two variables, confirming the formulated hypothesis.

Key words:
Burr function; light intensity; probabilistic models; temporal variation

RESUMO

O objetivo é estudar a dinâmica da radiação fotossintética alcançando a superfície do solo em povoamentos de Acacia mearnsii De Wild e sua influência no crescimento em altura em povoamentos. Este fato dá origem à formulação da seguinte hipótese para este estudo: "A redução da incidência de luz no interior do suporte de acácia negra vai fazer com que o ponto de inflexão no seu crescimento quando esta atinge a altura de 4 a 5 m de altura, isto é, quando o povoamento se encontra entre 2 e 3 anos de idade". O estudo foi realizado em povoamentos no Estado do Rio Grande do Sul, Brasil, onde os diâmetros a altura do peito, altura total e radiação fotossinteticamente ativa disponível ao nível do solo foram medidos. A frequência tendeu a ser mais intensa com o aumento da idade dos povoamentos. Ficou evidente que ocorreu redução da incidência de luz no interior da floresta causada pelo fechamento do dossel. Consequentemente, o dossel fechado propiciou a concorrência das plantas. Isso afetou as condições para o crescimento em diâmetro e altura dessa espécie, razão pela qual se torna possível conceber a ocorrência de um ponto de inflexão no crescimento dessas duas variáveis, confirmando a hipótese formulada.

Palavras-chave:
função de Burr; intensidade luminosa; modelos probabilísticos; variação temporal

INTRODUCTION

The black wattle ( Acacia mearnsiiDe Wild) is a prominent forest species in the state of Rio Grande do Sul, Brazil, whose stands only are smaller in area when compared to Eucalyptusand Pinusplantations.

The species is the main source of bark for the tannin industry worldwide, and its cultivation benefits nearly 40,000 families in Brazil, playing therefore an important socioeconomic role ( Stein and Tonietto 1997).

The light incidence in soil is fundamental for the tree height during the initial growth. With the reduction of the incidence of light in lower branches of trees they begin to die. This reduces photosynthesis, and consequently causes a reduction of height growth of young trees. This ends up causing the occurrence of an inflection point in this process.

The amount of radiation available at ground level inside the stand is a function of several factors, including physiological and morphological characteristics, such as growth pattern, leaf angle and leaf position of the species comprising the forest stand. Moreover, radiation is also determined by canopy characteristics, such as the location and size of small gaps in the canopy, commonly called sunflecks, as highlighted by Miller and Norman (1971).

In places covered with dense vegetation, only a small fraction of the sun's radiation reaches the ground and varies in space and time. Understanding this process, therefore, requires a mathematical function able to describe both the variation in radiation intensities in space (given by different intensities of radiation reaching the ground), and over time (given by the percentage of points that sustain a given intensity of radiation).

Probability density functions are among the most useful mathematical models for describing dynamics that takes place simultaneously in time and space. Therefore, it becomes important to analyze the evolution of the light incidence that affects the height growth rate. Consequently the fit of a hypsometric model is required to describe the height growth behavior for black wattle in this study.

This fact gives rise to the formulation of the following hypothesis for this study:

"The reduction of the incidence of light inside the stand of black wattle planted in initial spacing of (3 x 1.5 m) will cause the inflection point in its height growth when this reaches 4 to 5 m in height, i.e. when the stand is between 2 and 3 years of age".

MATERIALS AND METHODS

DATA COLLECTION OF THE INCIDENCE OF LIGHT INSIDE THE STAND OF BLACK WATTLE

Several commercial plantations of black wattle were selected from regions of high concentration of the species in the municipalities of Crystal and Piratini (Rio Grande do Sul, Brazil). In each municipality the stands were selected in a range of ages: one, three, five and seven years old.

In Cristal, the evaluated areas are located between coordinates 30° 54' South and 50° 40' West and in Piratini between 31° 25' South and 52° 58' West, all in the altitude of 320 to 370 meters above sea level.

The plantations in the two regions were established both, in newly cultivated areas (first rotation), as well as in previously cultivated areas (second rotation). The plantings were conducted at a spacing of 3 x 1.75 meters (1,904 plants per ha) for year one and 3 x 1.5 meters for all other ages (2,222 plants per ha).

The soils of the municipality of Cristal were classified as dystrophic regolitic neosols, whereas in Piratini they were classified as dystrophic litholic neosols according to EMBRAPA standards.

In each stand, a north-facing hillside was chosen in which three plots were installed at the top, middle and bottom of the slope. The plot size was 9 x 16 meters for the one-year-old stands and 9 x 14 meters for all other ages, for a total of four rows and 10 plants in each row.

In each stand, three sampling units with a subsampling of 15 points for the assessment of Photosynthetically Active Radiation (PAR) were established, i.e. in each stand 45 subsampling points were installed and in each of those points five readings were performed throughout the day, which resulted in 225 readings per stand. The evaluation of PAR consisted of performing 225 readings using a pyranometer (LI-COR 1600) throughout the day (7:30am, 9am, 12pm, 3pm, 4:30pm) within and outside the stand at each age and in each region, i.e. 450 measurements per age ( Fig. 1). All together, 8 stands were sampled, which resulted in 810 sampling points established and a total of 4.050 readings of PAR were performed inside the stands.

Figure 1
Readings of photosynthetically active radiation within (30 cm from the soil surface) stands of black wattle.

The sample points were systematically established within each plot in three different directions, one located within the row (1), another between each row (2), and the third at a 45° angle between points 1 and 2. At each sample point five stakes were installed at 28 cm from the ground level and spaced 75 cm apart. The first stake was set 38 cm from the tree whose diameter was roughly the average for the plot ( Fig. 1).

The readings were taken inside the stand at 30 cm from ground level. Readings outside of the stands (PAR incident on the stands) were performed in the open areas by taking five evaluations before and five after each measurement time.

From the readings inside and outside the stand the photosynthetically active radiation reaching the surface was calculated as follows:

PARss = ( PARt/ PARi) 100 (1)

Where:

PARss = photosynthetically active radiation reaching the soil surface (%);

PARt = PAR transmitted through the canopy reaching the soil surface; and

PARi = PAR incident upon the stand.

Probability Density Functions (PDF) to describe the incidence of light inside the stand of black wattle

We evaluated the following PDFs in their abilities to describe photosynthetically active radiation reaching the soil surface: Beta, Burr, Burr (four parameters), Dagum, Dagum (four parameters), Exponential (two parameters), Fatigue Life, Gamma (three parameters), Inverse Gaussian, Inverse Gaussian (three parameters), Johnson SB, Levy, Levy (two parameters), Log Pearson III, Log Normal (three parameters), Normal, Pearson V (three parameters), Pearson VI (four parameters) and Weibull (three parameters), presented in Johnson et al. (1995).

Initially, all functions were fitted using the Maximum Likelihood Method ( Fisher 1922), from which the best fit was selected. The best-performing probabilistic function was selected using a Kolmogorov-Smirnov test at 99% probability level (Kolmogorov 1933, Smirnov 1948).

Ten classes of ground-incident photosythetically active radiation were used in the fitting process: 0-10%, 10-20%, 20-30%, 30-40%, 40-50%, 50-60%; 60-70%, 70-80%, 80-90% and 90-100%. The middle points of classes were: 5%, 15%, 25%, 35%, 45%, 55%, 65%, 75%, 85% and 95%.

The data were evaluated using descriptive statistics. Besides the traditional statistics (mean, variance, standard deviation and percentiles), measures of skewness and kurtosis were used to describe the shape and the evolution of the distribution of frequencies of photosynthetically active radiation at ground level. These statistics were calculated according to Cochran and Cox (1957)and Steel and Torrie (1960).

The asymmetry was evaluated for the follo wing aspects:

No skewness: mode = median = arithmetic mean.

Positive skewness if: mode < median < arithmetic mean.

Negative skewness if: mode > median > arithmetic mean.

If the skewness coefficient occurs between 0.15 and 1 is considered moderate, and if it is greater that 1 is considered strong.

Meanwhile kurtosis is the degree of flatness or relative elevation of a distribution, usually with respect to the normal distribution. Pearson (1895, 1905) defined three types of curves that describe kurtosis:

Leptokurtic: distribution having a relatively high peak with negative excess, i.e. coefficient of kurtosis < 0.263.

Platykurtic: a more flattened curve, with positive excess, i.e. coefficient of kurtosis > 0.263.

Mesokurtic: intermediate curve, with kurtosis coefficient equal to 0.263.

After choosing the best fitting function, the curves are compared for significant differences using a chi-square (χ2) test. The χ2 was obtained by the formula:

χ 2= Σⁿ_i-1 (n fi − nFi) ² / ( n Fi) (2)

where:

fi = probability observed in class i;

Fi = probability calculated in class i; and

n = total frequency.

The test was applied to all age combinations, namely: 1 * 3, 1 * 5, 1 * 7, 3 * 5, 3 * 7, and 5 * 7, and the significances were verified at 1% probability.

To verify in which years the greatest chan ges occurred, an integral under the curve was calculated from the selected PDF to obtain an area occupied by a given range of classes, and the curves of these areas were drawn in relation to the age of the stand.

Finally, a simple linear regression analysis between the parameters of the selected function with the stand age was performed to establish their correlation.

DATA COLLECTION OF DIAMETER AT BREAST HEIGHT AND HEIGHTS OF TREES IN YOUNG AGES TO MONITOR THEIR GROWTH EVOLUTION

The study was conducted using data from an expe riment on areas belonging to the Agroclimatology Laboratory of the Federal University of Santa Maria, CampiCESNORS (Rio Grande do Sul, North Higher Education Center), located at 27° 22" S latitude; 53° 25" W longitude, at 480 m altitude, in the municipality of Frederico Westphalen, Rio Grande do Sul, Brazil, established in 2008.

The total experiment was conducted with four tree species: Acacia mearnsiiDe Wild (Black wattle), Eucalyptus grandisHill (Eucalyptus), Mimosa scabrellaBenth (Bracatinga) and Ateleia glaziovianaBaill (Timbo) at different spacings: 3.0 x 1.0 m, 3.0 x 1.5 m, 2.0 x 1.0 m, and 2.0 x 1.5 m, but only the black wattle was considered for the present work.

A bi-factorial 4x4 design was used in the experiment: four tree species and four spacing were conducted with three replicates. A randomized block design with split-plots was used.

Each block included 16 experimental units, throughout which the four species were distributed at all spacing levels. Each experimental unit had 45 plants in five lines and 12 central plants were evaluated.

The variables measured were diameter at breast height (dbh) and total height, with data collection every three months from the time when the plants reached 1.3 m in height.

Recent experiences have shown that the Näslund (1936) hypsometric function gives one of the best fit to data coming from planted tree species. This function has a very important peculiarity, i.e. it estimates the inflexion point and the asymptote of the hypsometric relation curve. This is achieved by estimating the coefficients "a" and "b", so that the fitted curve assumes a flexible pattern for a wide range of species.

The Näslund function presents very attractive mathematical characteristics by allowing the appro ximation of solutions with only some preliminary information of the species occurring in inventories of manmade forests. The Näslund's function is given by:

H −1.30 = D2 / (a + bD)2 (2)

H −1.30 = D2 / (a2 + 2abD + b2D2) (3)

H −1.30 = 1 / (a2 / D2 + 2ab D/ D2 + b2D2 / D2) (4)

H −1.30 = 1 / (β0 / D2+ β1 / D+ β2) (5)

Where:

H = Total height (m).

D = Diameter at breast height - dbh (cm)

a =Coefficient that explains the inflection point.

b =Coefficient that explains the asymptote.

β0 = a2; β1 = 2ab; β2 = b2

Taking the limit of the function for D → ∞ we get to asymptote of the Näslund function.

H −1.30 = 1 / (β0 / D2 + β1 / D+ β2) (6)

H = 1 / β2 + 1.30 = 1 / b2 + 1.30 (7)

The second derivative of the function set to zero results the inflection points of the function, as follows:

∂2H / ∂2D = 0 (8)

DInf = a / 2b (9)

HInf = 1/9b2 + 1.30 (10)

Where:

HInf = Height of the inflection point (m);

DInf = Diameter of the inflection point (cm).

The asymptote and the inflection points can be observed in Figure 2.

Figure 2
The asymptote and the inflection points.

RESULTS

INCIDENCE OF LIGHT INSIDE THE STAND OF BLACK WATTLE

Over time, the average photosynthetically active radiation reaching the soil surface tended to decrease in stands of black wattle ( Table I). As stand age increased there was no significant increase or decrease in the total amplitude of photosynthetically active radiation at ground level, with frequencies occurring in all classes originally proposed. Furthermore, lower levels of radiation intensity within the stand tended to be more common with increasing age.

TABLE I
Descriptive statistics of photosynthetic radiation levels (percentage) reaching the soils surface in one, three, five and seven year old black wattle stands.

Statistics	Value
	Year 1	Year 3	Year 5	Year 7
Average	33.47	24.77	26.38	19.43
Variance	680.56	529.85	673.02	454.56
Standard Deviation	26.09	23.02	25.94	21.32
Coefficient of Variation	0.78	0.93	0.98	1.10
Standard Error	1.23	1.09	1.22	1.01
Skew	0.68	1.36	1.21	1.81
Kurtosis	-0.78	1.06	0.34	2.58
Percentile	Value
	Year 1	Year 3	Year 5	Year 7
Minimum	0.18	0.27	0.57	0.98
5%	3.91	2.72	2.76	3.11
10%	5.49	3.93	3.621	4.42
25% (Q1)	10.67	7.69	0.58	6.56
50% (Median)	26.25	15.45	14.13	9.24
75% (Q3)	54.64	33.49	38.87	24.23
90%	75.90	63.21	72.00	53.05
95%	84.65	74.84	82.22	71.84
Maximum	96.74	99.67	97.80	97.66

The goodness of fit test for different PDFs for each age is shown in Table II. Of the 19 PDFs tested, the Kolmogorov - Smirnov test revealed that only the Burr function (four parameters) was flexible enough to represent the variability in radiation intensity across all age groups. Consequently, we present the fit results only for this function as it allowed us to describe a trend over several years, which was one of the objectives of the present study.

TABLE II
Kolmogorov - Smirnov Test for 19 PDFs to describe photosynthetically active radiation levels reaching the soil surface in black wattle stands, aged one, three, five and seven years.

Distribution	Kolmogorov-Smirnov
	Year 1	Year 3	Year 5	Year 7
Beta	0.07437ns	0.07851**	0.11596**	0.24603**
Burr	0.06848ns	0.05583ns	0.10288**	0.06885ns
Burr (4P)	0.06785ns	0.0535ns	0.07213ns	0.07347ns
Dagum	0.10856**	0.04283ns	0.07557ns	0.08972**
Dagum (4P)	0.10838**	0.0469ns	0.05852ns	0.09095**
Exponential (2P)	0.06672ns	0.04978ns	0.11593**	0.1693**
Fatigue Life	0.06879ns	0.0487ns	0.05199ns	0.14834**
Gamma (3P)	0.06987ns	0.05512ns	0.09122**	0.16702**
Inv. Gaussian	0.11015**	0.11365**	0.0748ns	0.14486**
Inv. Gaussian (3P)	0.16332**	0.04462ns	0.08101**	0.11822**
Johnson SB	0.02685ns	0.08201**	0.0748ns	0.1246**
Levy	0.2978**	0.24634**	0.24089**	0.2293**
Levy (2P)	0.2978**	0.22332**	0.20641**	0.20827**
Log-Pearson 3	no fit	0.04152ns	0.06403ns	0.10899**
Lognormal (3P)	0.07357**	0.04192ns	0.06791ns	0.12055**
Normal	0.12304**	0.16792**	0.21005**	0.25257**
Pearson 5 (3P)	0.12134**	0.05328ns	0.08433**	0.0972**
Pearson 6 (4P)	0.06974ns	0.05262ns	0.07972*	0.09878**
Weibull (3P)	0.06858ns	0.05278ns	0.0779**	0.1512**

• ns = not significant at 1% probability against the Kolmogorov-Smirnov distribution.
• **significant at 1% probability against the Kolmogorov-Smirnov distribution.

The properties of the Burr (4P) function can be found in Burr (1942) and Johnson et al. (1995). The Burr function is described by the following mathematical expression:

f( x) = a k(( x − γ / β)α − 1 / β (1+ (( x − γ) / β α) k+ 1 (11)

Where:

α, k = shape coefficient;

β = scale coefficient; and

γ = location coefficient.

The fit of the coefficients of the Burr function is presented in Table III.

TABLE III
Coefficients obtained for the Burr function (four parameters) to describe the photosynthetically active radiation reaching the soil surface in black wattle stands, aged one, three, five and seven years.

Stand Age	Coefficients		R2
	k	α	β	γ
1	5237.2	1.2574	32741	0	0.74
3	5.2087	1.2131	87.492	0.25226	0.95
5	3.3754	1.1294	60.093	0.51354	0.91
7	0.14968	10.063	10.6	-6.3023	0.71

The fit of the function for both observed and predicted values is presented in Fig. 3.

Figure 3
Burr function (4P) describing the photosynthetically active radiation incident upon soil surface in acacia stands aged one year (a), three (b), five (c), and seven (d) years.

When fitting a probability distribution to a dataset, the accepted hypothesis is that the distribution may adequately represent these circumstances. This characteristic allows us to evaluate the dynamics over time through changes in the shape of the curve. The shape of the curve is determined by coefficients obtained in each year of fitting.

There was no significant increase or decrease in width of the total photosynthetically active radiation at ground level over time, with similar levels occurring in all classes originally proposed (0%-100%) (Table II). The indices of skewness and kurtosis indicated left skewed distributions, i.e. positive for all ages. The kurtosis profile revealed a platykurtic shape in year one (-0.78), becoming leptokurtic (1.06, 0.34, 2.58, respectively) in the subsequent age groups (3-7 years). The distribution showed moderate skewness (0.68) only in the first year of the stand, becoming more pronounced in the following years (1.36, 1.21 and 1.81). Therefore, with increasing age, left-skewed curves became more accentuated and less flattened.

To evaluate the dynamics of photosynthetically active radiation reaching the soil in stands of black wattle over time, and the effect of age on the curves estimated by the Burr function, curves of the fitted function were plotted for each age. The frequency of points with lower radiation intensities tended to increase with age, causing the curve to become more acute and shifted to the left ( Fig. 4).

When the differences between curves (with respect to stand age, Fig. 3) were examined analytically by Chi-square (χ2), 3 year-old stands were not significantly different from 5 year-old stands (p > 0.05), implying the absence of significant differences between the expected and actual values ( Table IV). This situation is also reflected in the behavior of the areas occupied by the curves in relation to age of the stand ( Fig. 4).

TABLE IV
Chi-square (χ2) test between the curves generated by the Burr function to describe the availability of photosynthetically active radiation at ground level in 1, 3, 5 and 7 year-old black wattle stands.

Stand Age Combination	χ2	α
1 * 3	80.12	1.3E-14
1 * 5	95.71	8.28E-18
1 * 7	557.63	3.20E-116
3 * 5	4.35	0.74
3 * 7	207.49	2.97E-41
5 * 7	162.91	7.84E-32

Figure 4
Dynamics of photosynthetically active radiation reaching the soil surface in black wattle stands aged one, three, five and seven years.

A simple linear regression analysis resulted in strong correlations between all parameters of the Burr function and stand age. The estimators k, β and γ tended to decrease with age, a fact verified by evaluating the correlation between these parameters and age, resulting in negative values of 0.78, 0.78 and 0.73 for each of the estimators, respectively. Meanwhile, the α parameter tended to increase, showing a positive correlation of 0.77. The strong correlations and similarities between all parameters indicate good prospects to recommend this distribu tion for describing radiation available at ground level.

DIAMETER AT BREAST HEIGHT AND HEIGHTS OF TREES IN YOUNG AGES OF BLACK WATTLE TO MONITOR THEIR GROWTH EVOLUTION

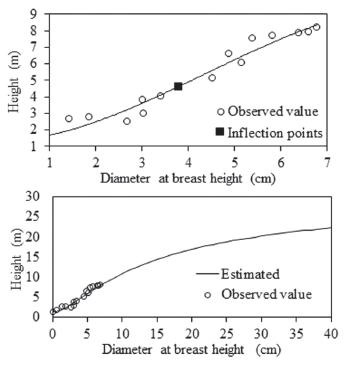
In the first years of growth it was possible to obtain the inflection points and asymptote for black wattle, to the derived equations from Näslund, as can be seen in Figure 6.

Figure 5
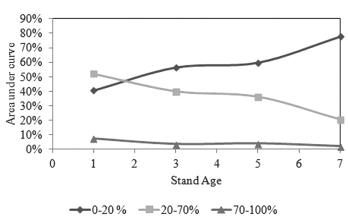
The area under the curves (given by the integral of the Burr function) as a function of photosynthetically active radiation class at ground level, in one, three, five and seven year old black wattle stands.

Figure 6
Hypsometric relationship with the indication of the inflexion points and asymptot for black watlle in Frederico Westphallen, Rio Grande do Sul, Brazil.

The estimated coefficients "a" and "b" as well as the values of asymptote and inflection points of the hypsometric relation found for the black wattle curve are shown in Table V.

TABLE V
Estimated parameters for the Näslund function (1936), inflexion points and asymptote for black wattle in Frederico Westphalen, Rio Grande do Sul, Brazil.

a	b	Height of the Asymptote (m)	Inflexion Points
			DBH (cm)	Height (m)
1.3946	0.1835	31.0	3.8	4.6

DISCUSSION

Various researchers have measured photosyntheti cally active radiation at ground level in different forest types. Overall, 80% of the incident solar radiation is intercepted by tree canopies and less than 5% reaches the forest floor ( Geiger 1950, Yoshino 1975). Stape et al. (2004)evaluating Eucalyptus manmade forests observed that photosynthetic radiation interception in stands with different management regimes ranged from 65% to 68%. In other studies, radiation at ground level, such as in pine forests, by Gay et al. (1971), were observed average levels of 18%; in pine forest, by Chen et al. (1993), of 3.7 to 5.7% and in conifer forest, by Carlson and Groot (1997), of 18% were observed.

Kittredge (1948)mentioned that the percentage of solar radiation transmitted to the interior of a pine forest in the United States was 17% and ranged from 0.7 to 16% for walnut. In the Amazon rainforest, radiation at ground level observed by Shuttleworth et al. (1984)was on average 1.2%; in deciduous forests it was 6% according to Morecroft et al. (1998)and 1.5% in pine forest according to Chen et al. (1999). When compared to these values ​​from the literature, the results for black wattle from the present study showed higher incidence radiation levels inside the stand.

The Burr function has rarely been used in the field of forestry compared to other more traditional functions such as the Normal, Log-normal, Gamma, Beta, Johnson SB, and Weibull. The Burr probability function (four parameters) is flexible enough to represent the variability in the availability of photosynthetically active radiation at ground level in stands of black wattle. Binoti et al. (2012)evaluated the effectiveness of Fatigue Life, Frechet, Gamma, generalized Gamma, generalized Logistic, Log-logistic, Nakagami, Beta, Burr, Dagum, Weibull and hyperbolic distributions, to describe the diameter distribution in teak stands ( Tectona grandis L.) subjected to thinning at different ages, and concluded that the Log-Logistic (3P), Burr (3P), hyperbolic (3P), Burr (4P), Weibull (3P), Hyperbolic (2P), Fatigue Life (3P) and Nakagami functions yielded Kolmogorov-Smirnov tests results more satisfactory than the Weibull function, which is the most commonly found in the literature.

Probability functions have also been used to describe the frequency of weather elements, such as solar radiation, air temperature and wind velocity. For example, García et al. (1998), Lun and Lam (2000), Ramírez and Carta (2006), and Carta and Ramírez (2007)evaluated probability distributions to model the wind speed, and it was found by all of them that the Weibull function was adequate, except when it came to bimodal distributions ( Carta et al. 2009). Assunção et al. (2003)used the Beta Function to model the incidence of solar radiation. Murphy and Wilks (1998)also utilized this function to evaluate the probability of precipitation. Kyselý (2002)used the Gumbel function to model the maximum temperature distribution.

Comparing the curves analytically, three features are highlighted in Figure 3: the first refers to the point where the curves meet, change direction (point 1) and become more pronounced; the second denotes a certain difference between the curves that remains approximately constant; and the third which indicates a point where the curves begin to converge and the differences are reduced. The points are explicitly represented in Figure 7.

Figure 7
Dynamics of photosynthetically active radiation reaching the soil surface in stands of black wattle, aged one, three, five and seven years.

The first region in Figure 6represents points inside the stand coming from shade caused by the denser layers of the canopy, i.e. largest leaf area and branch volume. The projections of these points on ground level, which depend on the angle of incidence of solar radiation on the canopy or the time of the day, will result in lower radiation intensities. These sites roughly correspond to the first two radiation classes proposed, i.e. up to 20% of photosynthetically active radiation reaching ground level.

In region 2, the points represent areas located near the edges of the canopy, i.e. the transition between the space occupied by the crown and open sky, as well as the few small gaps in the canopy. These points roughly correspond to the second through seventh classes, i.e. 20% to 70% of photosynthetically active radiation reaching ground level.

Region 3 in the figure refers to the points receiving the highest radiation intensities, i.e. the gaps between individual tree crowns (usually at the halfway point between adjacent plantation rows) and also the largest gaps in the canopy. At these points the highest levels of light are transmitted into the interior of the stand and, in this case, are the points corresponding to classes above 70% incidence of photosynthetically active radiation at ground level. Generally, these sites, commonly called sunflecks (Miller and Norman 1971), have spectral profiles equal to direct sunlight, though reduced in intensity ( Evans 1965).

Evidently the biggest changes in the ground-level radiation dynamics occur at points 1 and 2, i.e. classes smaller than 70% ( Fig. 5). At these points, the changes depend on the growth of the tree canopy intercepting the bulk of the solar radiation in a forest stand. Thus, as the tree canopy grows, so does the volume of solar radiation it intercepts. In other words, as the density of the canopy increases with age, so does the volume under the curve in the range of 0%-20%.

Consequently, the area under the curve in the 20%-70% range decreases as the points that promote the occurrence of these light intensities become less frequent in the canopy structure of the stand, because a) the canopy begins interlacing at the edges (especially along the row), and b) because the tree grows both in leaf area and branch volume, occupying more space in the canopy. Thus, the classes between 0%-20% and 20-70% become inversely proportional, which can be verified by the negative correlation between these classes as the stand ages ( Table VI).

TABLE VI
Correlation between the areas occupied by the availability of different classes of photosynthetic radiation ground level in 1, 3, 5 and 7 years old stands of black wattle.

Photosynthetically active radiation available at ground level		0%-20%	20%-70%	70%-100%
0%-20%	1.000
20%-70%	-0.999	1.000
70%-100%	-0.947	0.928	1.000

The observed results are consistent with those of Hardy et al. (2004), who report that the amount of radiation intercepted by a forest and consequently the radiation that reaches the ground level is determined by characteristics of the canopy as well as the size of the existing gaps in the canopy. Consequently, the probability of photosynthetically active radiation reaching the ground is inversely proportional to the degree to which it is intercepted by the canopy structure of the stand.

The incidence of radiation class over 70% almost did not change over the years ( Fig. 5), therefore it can be said that the species and the current spacing of the stand, even after years of growth, allowed higher light penetration inside. Consequently, a favorable environment has been created to the establishment and development of the understory species.

The effect of sun position throughout the day is another important feature in stands of black wattle in combination with canopy structure. This allows light transmission of different intensities into the interior of the stand, with little change in the frequencies of intensities greater than 70% of the available photosynthetically active radiation at ground level.

As is known, the incidence radiation within a stand varies at a given point throughout the day and therefore depends on the angle between the zenith and the sun, which results in the angle of sunlight incidence with respect to the treetops. This situation affords higher light intensities (represented in the 70%-100% range) on several locations inside a black wattle stand and provides conditions for the establishment of various plant species.

Longman and Jenik (1981)also show that the amount of light reaching the forest floor depends on the canopy structure and the position of the sun relative to the ground. The acute angle of incidence in the early morning and late afternoon increases the path length of light rays through the canopy. Thus, the relative radiation intensity in the forest soil is diminished considerably, since the oblique rays are blocked by leaves, branches and trunks.

After all these reviews and assessments of the incidence of light inside black wattle forests, the effects of reduced light in the forests were related to the growth of the variables: diameter at breast height and tree height during the first years after planting, accompanied by continuous quarterly inventory of permanent plots.

We are convinced of the evidence that there was a reduction of incidence of light inside the forest, caused by canopy closure. Consequently, closed canopy propitiated the competition of plants. This affected the conditions for growth in diameter and height of this species, which is why it was possible to conceive the occurrence of an inflection point in the growth of these two variables, confirming the hypothesis already formulated and illustrated in Figure 6.

The inflection point was set between 3 and 4 years, when the light inside the stands became scarce and did not allow the continuous acceleration of height growth. This also resulted in a process of competition for nutrients in the stand.

Such mathematical modeling is crucial for forest management of this species. It was possible to obtain a hypsometric function capable of allowing the prognosis of heights and, consequently, of the future volume of these stands.

ACKNOWLEDGMENTS

The authors thank TANAGRO S.A. Company, and the Agroclimatology Laboratory of Santa Maria's Federal University and the Research Excellency Center for Carbon Sink in Biomass for the collaboration in this research. They would also like to acknowledge Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for granting a scholarship at doctor's degree level for Alexandre Behling.

REFERENCES

• ASSUNÇÃO HF, ESCOBEDO JF and OLIVEIRA AP. 2003. Modeling frequency distributions of 5 minute-averaged solar radiation indexes using Beta probability functions. Theor Appl Climatol 75: 213-224.
• BINOTI DHB, BINOTI MLMS, LEITE HG, FARDIN L and OLIVEIRA JC. 2012. Probability density functions for description of diameter distribution in thinned stands of Tectona grandis. Cerne 18: 185-196.
• BURR IW. 1942. Cumulative frequency distribution. Ann Math Statist 13: 215-232.
• CARLSON DW and GROOT A. 1997. Microclimate of clear-cut, forest interior, and small openings in trembling aspen forest. Agr Forest Meteorol 87: 313-329.
• CARTA JA and RAMÍREZ P. 2007. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions. Renew Energ 32: 518-531.
• CARTA JA, RAMÍREZ P and VELÁZQUEZ S. 2009. A review of Wind speed probability distributions used on wind energy analysis: Case studies in the Canary Islands. Renew Sust Energ Rev 13: 933-955.
• CHEN J, FRANKLIN JF and SPIES TA. 1993. Contrasting micro¬climates among clearcut, edge, and interior of old-growth Douglas-fir forest. Agr Forest Meteorol 63: 219-237.
• CHEN J, SAUNDERS SC, CROWN TR, NAIMAN RJ, BROSOFSKE KD, MROZ GD, BROOKSHIRE BL and FRANKLIN J. 1999. Microclimate in forest ecosystem and landscape ecology. Bioscience 49: 288-297.
• COCHRAN WG and COX GM. 1957. Experimental designs. 2nd ed., London: J Wiley & Sons, 611 p.
• EVANS GC. 1965. Model and measurement in the study of woodland light climates. In: Bainbridge R, Evans GC and Rackham O (Eds), Light as an ecological factor. Wiley-Interscience, New York, NY, USA, p. 53-76.
• FISHER RA. 1922. On the mathematical foundations of theoretical statistics. Philos Trans R Soc Lond 222: 309-368.
• GARCÍA A, TORRES JL, PRIETO E and De FRANCISCO A. 1998. Fitting wind speed distributions: a case study. Sol Energy 62: 139-144.
• GAY LW, KNOERR KR and BRAATEN MO. 1971. Solar radiation variability on the floor of a fine plantation. Agr Meteorol 8: 39-50.
• GEIGER R. 1950. The climate near the ground. 2nd ed., Cambridge: Harvard University Printing Office, 482 p.
• HARDY JP, MELLOH R, KOENIG G, MARKS D, WINSTRAL A, POMEROY JW and LINK T. 2004. Solar radiation transmission through conifer canopies. Agr Forest Meteorol 126: 257-270.
• JOHNSON NL, KOTZ S and BALAKRISHNAN N. 1995. Conti¬nuous univariate distributions. 1st ed., Applied Probability and Statistics. New York: J Wiley & Sons, 732 p.
• KITTREDGE J. 1948. Forest influence: the effects of wood vegetation on climate, water and soil, with applications to the conservation of water and control of floods and erosion. New York: MacGraw-Hill, 394 p.
• KOLMOGOROV A. 1933. Sulla determinazione empirica di una legge di distribuzione. G Ist Ital Attuari 4: 83-91.
• KYSELÝ J. 2002. Probability estimates of extreme temperature events: stochastic modeling approach vs. extreme value distributions. Studia Geoph et Geod 46: 93-112.
• LONGMAN KA and JENIK J. 1981. Tropical forest and its environment. New York: Longman Scientific & Technical, 347 p.
• LUN IYF and LAM JC. 2000. A study of Weibull parameters using long-term wind observations. Renew Energ 20: 5-153.
• MILLER EE and NORMAN JMA. 1971. Sunfleck theory for plant canopies. I. Lenghts of sunlit segments along a transect. Agron J 63: 735-738.
• MORECROFT MD, TAYLOR ME and OLIVER HR. 1998. Air and soil microclimates of deciduous woodland compared to an open site. Agr Forest Meteorol 90: 141-156.
• MURPHY AH and WILKS DS. 1998. A case study of the use of statistical models in forecast verification: precipitation probability forecasts. Weather Forecast 13: 795-810.
• NÄSLUND M. 1936. Skogsförsöksanstaltens gallringsförsök i tallskog. Meddelanden från Statens skogsförsöksanstalt 29: 1-121.
• PEARSON K. 1895. Contributions to the mathematical theory of evolution, II: Skew variation in homogeneous material. Philos Trans R Soc Lond Ser A Math Phys Eng Sci 186: 343-414.
• PEARSON KR. 1905. Skew variation, a Rejoinder. Biometrika 4: 169-212.
• RAMÍREZ P and CARTA JA. 2006. The use of wind probability distributions derived from the maximum entropy principle in the analysis of wind energy: A case study. Energ Convers Manage 47: 2564-2577.
• SHUTTLEWORTH WJ, GASH JHC and LLOYD CR. 1984. Obser¬vations of radiation exchange above and below Amazonian forest. Quart J Roy Meteor Soc 110: 1163-1169.
• SMIRNOV N. 1948. Table for estimating the goodness of fit of empirical distributions. Ann Math Stat 19: 279-281.
• STAPE JL, BINKLEY D and RYAN MG. 2004. Eucalyptus production and supply, use and efficiency of the use of water, light and nitrogen across a geographic gradient in Brazil. Forest Ecol Manag 193: 17-31.
• STEEL RGD and TORRIE JH. 1960. Principles and procedures of statistics. New York: McGraw-Hill, 481 p.
• STEIN PP and TONIETTO L. 1997. Black Wattle Silviculture in Brazil. In: Brown AG and Ko HC (Eds), Black Wattle and its Utilization. RIRDC, Barton, MI, EUA, p. 78-82.
• YOSHINO MM. 1975. Climate in a small area: an introduction to local meteorology. Tokyo: University of Tokyo Press, 549 p.

Publication Dates

• Publication in this collection
  15 Sept 2015
• Date of issue
  Sept 2015

History

• Received
  17 Feb 2014
• Accepted
  18 Dec 2014