Abstract
Central composite rotatable design (CCRD) and artificial neural networks (ANN) have been applied to optimize the performance of nanofluid systems. In this regard, the performance was evaluated by measuring the stability and thermal conductivity ratio based on the critical independent variables such as temperature, particle volume fraction and the pH of the solution. A total of 20 experiments were accomplished for the construction of second-order polynomial equations for both target outputs. All the influential factors, their mutual effects and their quadratic terms were statistically validated by analysis of variance (ANOVA). According to the results, the predicted values were in reasonable agreement with the experimental data as more than 96% and 95% of the variation could be predicted by the respective models for zeta potential and thermal conductivity ratio. Also, ANN proved to be a very promising method in comparison with CCD for the purpose of process simulation due to the complexity involved in generalization of the nanofluid system.
Keywords
Nanofluid; Central composite design; Artificial neural network; Statistical; Stability; Thermal conductivity
INTRODUCTION
Nowadays, ultrahigh-performance of heating and cooling systems is one of the most vital needs of many industrial technologies, including power stations, production processes, transportation, and electronics. Many solutions such as heat surface addition (fins), vibration of the heated surface, injection or suction of fluid, applying electric or magnetic fields, and suspending nanoparticles with average sizes below 100 nm in fluids have emerged as solutions to support future heat exchanging systems across the globe. Among the various techniques that have been introduced to improve the thermal performance, nanofluids in which nano-sized metallic or nonmetallic particles are suspended uniformly in base fluids such as water, ethylene glycol, etc. are particularly promising. The nanofluids are expected to have better thermophysical properties compared to conventional heat transfer fluids (Zeinali Heris et al., 2007Zeinali Heris, S., Nasr Esfahany, M., Etemad, S. Gh., Numerical investigation of nanofluid laminar convective heat transfer through a circular tube. Numer. Heat Transfer-Part A: Applications, 52, 1043-1058 (2007).; Das et al., 2008Das, S. K., Choi, S. U. S., Yu, W., Pradeep, T., Nanofluids: Science and Technology. John Wiley & Sons, Hoboken, New Jersey (2008).; Kazemi-Beydokhti et al., 2013Kazemi-Beydokhti, A., Azizi-Namaghi, H., Zeinali Heris, S., Identification of the key variables on thermal conductivity of CuO nanofluid by a fractional factorial design approach. Numer. Heat Transfer-Part B, Fundamentals, 64, 480-495 (2013).). Long-term stability and thermal conductivity of nanofluids are important factors that have been widely investigated by many researchers for copper, aluminum, and titania nanoparticles with their oxides and carbon nanotubes (Murshed et al., 2005Murshed, S. M. S., Leong, K. C., Yang, C., Enhanced thermal conductivity of TiO2–water based nanofluids. Int. J. Therm. Sci., 44, 367-373 (2005).; Eastman, 2001Eastman, J. A., Choi, S. U. S., Li, S., Yu, W., Thompson, L. J., Anomalously increased effective thermal conductivities of ethylene glycolbased nanofluids containing copper nanoparticles. Appl. Phys. Lett., 78, 718-720 (2001).; Hwang, 2006Hwang, Y. J., Ahn, Y. C., Shin, H. S., Lee, C. G., Kim, G. T., Park, H. S., Lee, J. K., Investigation on characteristics of thermal conductivity enhancement of nanofluids. Curr. Appl. Phys., 6, 1068-1071 (2006).; Das et al., 2003aDas, S. K., Putra, N., Thiesen, P., Roetzel, W., Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat Transfer, 125, 567-574 (2003a).; Jiang and Wang, 2010Jiang, W., Wang, L. Q., Copper nanofluids: Synthesis and thermal conductivity. Curr. Nanosci., 6, 512519 (2010).; Lee et al., 1999Lee, S., Choi, S. U. S., Li, S., Eastman, J. A., Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transf., 121, 280-289 (1999).; Salehi et al., 2011Salehi, H., S. Zeinali Heris, H., Koolivand Salooki, M., Noei, S. H., Designing a neural network for closed thermosyphon with nanofluid using genetic algorithm. Braz. J. Chem. Eng., 28(1), 157168 (2011).; Wang and Mujumdar, 2008(aWang, X. Q., Mujumdar A. S., A review on nanofluids - part II: Experiments and applications. Braz. J. Chem. Eng., 25(4), 631-648 (2008a).,b)Wang, X. Q., Mujumdar, A. S., A review on nanofluids – part I: Theoretical and numerical investigations. Braz. J. Chem. Eng., 25(4), 613-630 (2008b).; Molana and Banooni, 2013Molana, M. and Banooni, S., Investigation of heat transfer processes involved liquid impingement jets: A review. Braz. J. Chem. Eng., 30 (3), 413435 (2013).).
Factors such as temperature, particle volume fraction, average primary particle size (APPS), pH of the nanofluid, elapsed time, ultrasonication (power and time), additive, base fluid and nanoparticle materials affect the performance of nanofluid systems with different degrees of sensitivities. Kazemi-Beydokhti et al. (2013)Kazemi-Beydokhti, A., Azizi-Namaghi, H., Zeinali Heris, S., Identification of the key variables on thermal conductivity of CuO nanofluid by a fractional factorial design approach. Numer. Heat Transfer-Part B, Fundamentals, 64, 480-495 (2013). applied a full foldover fractional factorial design (FFD) ( 2III7-4) in order to determine which of the factors temperature, particle volume fraction, APPS, pH of the nanofluid, elapsed time, sonication time and density of the nanoparticles and their binary interactions have the greatest influence on the results. The analysis of variance revealed that three factors, including the temperature, particle volume fraction and pH of the nanofluid, have the most significant effect on the response variable. Among the various types of nanoparticles, tin dioxide, which has excellent chemical and physical stability, is not widely used, although it is a cheap and commercially available mineral product. In addition, our previous work (Habibzadeh et al., 2010Habibzadeh, S., Kazemi-Beydokhti, A., Khodadadi, A. A., Mortazavi, Y., Omanovic, S., Shariat-Niassar, M., Stability and thermal conductivity of nanofluids of tin dioxide synthesized via microwave-induced combustion route. Chem. Eng., J., 156, 471-478 (2010).) on tin dioxide nanofluid confirms that these three factors have a significant effect on stability and the thermal conductivity ratio.
The traditional methods of optimization such as one-factor-at-a-time (OFAT) experimental technique for multivariable systems can be used. However it is well accepted that this is time-consuming, excessive in cost, complicated and might provide the researcher with wrong conclusions. Also, factorial design is weak in estimating quadratic terms and introducing enough curvature into the response surface (Montgomery and Runger, 2003Montgomery, D. C., Runger, G. C., Applied Statistics and Probability for Engineers. 3rd Ed., John Wiley & Sons, New York, U.S.A (2003).; Gheshlaghi, 2007Gheshlaghi, R., Optimization of Recombinant Protein Production by a Fungal Host. Ph.D. Thesis, Waterloo, Ontario, Canada (2007).; Gheshlaghi et al., 2008Gheshlaghi, R., Scharer, J. M., Moo-Young, M., Douglas, P. L., Application of statistical design for the optimization of amino acid separation by reverse-phase HPLC. Anal. Biochem., 383, 93-102 (2008).). To overcome such difficulties, a neural network and a multi-step statistical optimization strategy involving factorial design and response surface methodology (RSM) have been developed to analyze the effects of the process parameters on stability and the thermal conductivity of the nanofluid system. On the other hand, these techniques are good mathematical tools to build models, optimize the experimental results and obtain the optimal values of the output and input variables.
To the best of our knowledge, these techniques have not been applied for optimization of the main factor levels of stability and the thermal conductivity ratio of nanofluids. Therefore, the main objective of this study was to find the optimum conditions for maximizing the stability and thermal conductivity ratio of a tin dioxide nanofluid. In this regard, three independent variables, including temperature, particle volume fraction and solution pH, were selected for modeling and optimization.
THEORETICAL
Response Surface Methodology (RSM)
Designing experiments is a statistically basic technique to obtain the most information in order to improve the performance of a manufacturing process from the fewest experimental runs. Among the various methods of designing experiments, response surface methodology is a combination of mathematical and statistical techniques that are useful for modeling and analyzing the influence of several design variables on the response and the objective is to optimize this response (Montgomery and Runger, 2003Montgomery, D. C., Runger, G. C., Applied Statistics and Probability for Engineers. 3rd Ed., John Wiley & Sons, New York, U.S.A (2003).; Gheshlaghi, 2007Gheshlaghi, R., Optimization of Recombinant Protein Production by a Fungal Host. Ph.D. Thesis, Waterloo, Ontario, Canada (2007).). The quadratic coefficients in the second-order model may be evaluated by applying 3 levels (at least) for each independent factor. As the number of independent factors increases in 3n factorial design, the number of required runs rapidly increases. Obviously, this may be unacceptable and lead to overkill if the experiments are time-consuming and costly. The central composite design (CCD) is a sequential design strategy which reduces the number of experiments to get close to the 2-level full factorial design. Thus, 2n points of the full factorial twolevel design may be combined with some center point repetition of nominal design and 2n axial runs to yield a CCD (Gheshlaghi, 2007Gheshlaghi, R., Optimization of Recombinant Protein Production by a Fungal Host. Ph.D. Thesis, Waterloo, Ontario, Canada (2007).; Gheshlaghi et al., 2008Gheshlaghi, R., Scharer, J. M., Moo-Young, M., Douglas, P. L., Application of statistical design for the optimization of amino acid separation by reverse-phase HPLC. Anal. Biochem., 383, 93-102 (2008).).
In this regard, in the present study, RSM based on the CCD has been applied for the modeling of the nanofluid system with the aid of Design Expert version 8.0.7.1 statistical software (Stat-Ease Inc.). Three independent design variables, namely temperature (X1), particle volume fraction (X2) and solution pH (X3), were investigated with the actual and coded values shown in Table 1.
The levels of other factors such as particle size and sonication time were selected as 5 nm and 2 hours, respectively. Also, the measurements of zeta potential and thermal conductivity were done immediately after the preparation step.
For the three factors, CCRD with a quadratic model is composed of the full 23 factors with its 8 cubic points, augmented with six replications of the center points and the six axial (star) points. Central composite designs with different properties can be developed by taking different α values. To make the design rotatable, the axial distance α was assigned a value of 1.68. Rotatable design makes the variance of prediction depend only on the scaled distance of the center of the design (Akhtar, 2001Akhtar, M., Five-factor central composite designs robust to a pair of missing observations. J. Res. Sci., 12(2), 105-115 (2001).; Proust 2010Proust, M., Design of Experiments Guide. SAS Institute Inc., Cary, NC, USA (2010).). The CCD for the three independent factors is represented in Figure 1.
To evaluate the efficiency of the statistical design of the experiment based on RSM, a multilayer feedforward ANN was calculated.
Artificial Neural Networks (ANNs)
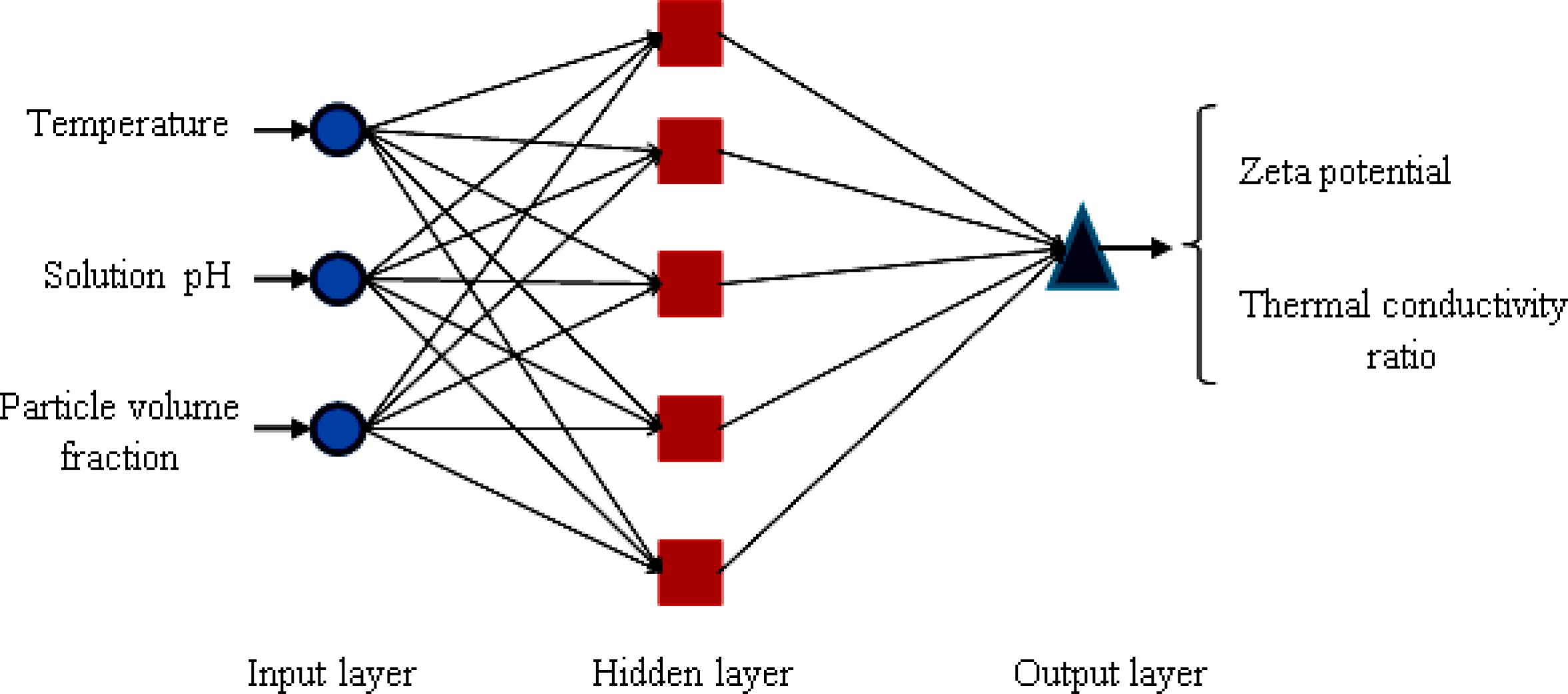
In recent years, the application of ANN has been developed as a powerful and flexible mathematical tool for modeling nonlinear and intricate systems. Also, an ANN can be considered as a massively parallel distributed processor, which transfers the knowledge and rules existing beyond the experimental data into the network structure for further applications (Rahmanian et al., 2011Rahmanian, B., Pakizeh, M., Mansoori, S. A. A., Abedini, R., Application of Experimental design approach and Artificial Neural Network (ANN) for the determination of potential micellar-enhanced ultrafiltration process. J. Hazard Mater. 187, 67-74 (2011).; Shanbedi et al., 2013Shanbedi, M., Jafari, D., Amiri, A., Zeinali Heris, S., Baniadam, M., Prediction of temperature performance of a two-phase closed thermosyphon using artificial neural network. Heat Mass Transfer, 49, 65-73 (2013).; Salehi et al., 2013Salehi, H., Zeinali Heris, S., Esfandyari, M., Koolivand, M., Nero-fuzzy modeling of the convection heat transfer coefficient for the nanofluid. Heat Mass Transfer, 49, 575-583 (2013).; Shanbedi et al., 2014Shanbedi, M., Zeinali Heris, S., Amiri, A., Adyani, S., Alizadeh, M., Baniadam, M., Optimization of thermal efficiency of a two-phase closed thermosyphon using active learning on the human algorithm interaction. Numer. Heat Transfer-Part A: Applications, 66(8), 947-962, (2014).). In this study, a multilayer feed-forward neural network has been used to design the complex nonlinear relationships between input and output layers. Each layer has a specific number of neurons that play a significant role in the modeling of the system. The neurons in the input layer receive the data and then distribute them. The hidden layer processes and organizes the data received from the input layer and delivers them to the output layer (Yousefi et al., 2012Yousefi, F., Karimi, H., Papari, M. M., Modeling viscosity of nanofluids using diffusional neural networks. J. Mol. Liq., 175, 85-90 (2012).). The output layer is the product of all the incoming signals. Finally the network was trained by using the Levenberg–Marquardt (LM) algorithm. The structure of this network is shown in Figure 2 schematically.
EXPERIMENTAL
Preparation of SnO2 Nanoparticles
In this study, the SnO2 nanoparticles were synthesized through a novel technique named chloride solution combustion synthesis (CSCS) and its associated nanofluids were prepared by using the two-step method described elsewhere (Zeinali Heris et al., 2007Zeinali Heris, S., Nasr Esfahany, M., Etemad, S. Gh., Numerical investigation of nanofluid laminar convective heat transfer through a circular tube. Numer. Heat Transfer-Part A: Applications, 52, 1043-1058 (2007).; Habibzadeh et al., 2010Habibzadeh, S., Kazemi-Beydokhti, A., Khodadadi, A. A., Mortazavi, Y., Omanovic, S., Shariat-Niassar, M., Stability and thermal conductivity of nanofluids of tin dioxide synthesized via microwave-induced combustion route. Chem. Eng., J., 156, 471-478 (2010).). In addition, microwaves were used for fast and homogeneous heating of the combustion synthesis solutions in the synthesis of SnO2 nanoparticles. The vibration ran for two hours using an ultrasonic processor (Bandelin Sonoplus model HD3200, power density-200 watts, frequency-20 kHz). Afterwards, the crystalline structures and approximate sizes of the SnO2 nanoparticles were determined by X-ray powder diffraction (XRD) with a Philips-X’pert diffractometer using Cu Kα radiation (λ= 1.54056 Å). The crystal size of the SnO2 powders was determined by applying the Scherrer formula on the (1 1 0) diffraction peak. The BET surface area measurement was also carried out by nitrogen adsorption after degassing of the samples at 300 °C for 2 hours, using a Quantachrome CHEMBET-3000 apparatus. All other information was mentioned in our previous work (Habibzadeh et al., 2010Habibzadeh, S., Kazemi-Beydokhti, A., Khodadadi, A. A., Mortazavi, Y., Omanovic, S., Shariat-Niassar, M., Stability and thermal conductivity of nanofluids of tin dioxide synthesized via microwave-induced combustion route. Chem. Eng., J., 156, 471-478 (2010).).
Sodium dodecyl sulfate, as an anionic surfactant, with the concentration of 0.1 mM, was selected and added in the preparation of nanofluids for better dispersion of nanoparticles. Long term stability was not necessary for the measurement of thermal conductivity of nanofluids by the Transient Hot Wire (THW) method because the measurements were made only a few seconds after preparation. Generally, the nanofluids used in this study did not settle for at least 4 hours. Fluids with settling times less than three hours were excluded from the experiments.
Measurement of the Stability and Thermal Conductivity of the Nanofluid
Investigations show that clustering and aggregation are main features in the stability and extraordinary enhancement of the thermal conductivity of nanofluids (Evans et al., 2008Evans, W., Prasher, R., Fish, J., Meakin, P., Phelan, P., Keblinski, P., Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids. Int. J. Heat Mass Transfer, 51, 1431-1438 (2008).; Tucknott and Yaliraki, 2002Tucknott, R., Yaliraki, S. N., Aggregation properties of carbon nanotubes at interfaces. Chem. Phys., 281, 455-463 (2002).). Hence, if we can prepare a more highly homogenized nanofluid, the stability and thermal conductivity of the nanofluid should be better. A stable suspension requires a good dispersion of the small particle in the liquid medium and a higher absolute value of the zeta potential of the particles (Tucknott and Yaliraki, 2002Tucknott, R., Yaliraki, S. N., Aggregation properties of carbon nanotubes at interfaces. Chem. Phys., 281, 455-463 (2002).). Then, zeta potential was measured by a Malvern Nano-ZS (Malvern Instrument Inc., London, UK). The pH was controlled by using hydrochloric acid (HCl) and sodium hydroxide (NaOH) of analytical grade. Thermal conductivity measurements were performed by a THW technique, which is known to be an accurate method for determining the thermal conductivity of fluids. The details are elaborated elsewhere (Habibzadeh et al., 2010Habibzadeh, S., Kazemi-Beydokhti, A., Khodadadi, A. A., Mortazavi, Y., Omanovic, S., Shariat-Niassar, M., Stability and thermal conductivity of nanofluids of tin dioxide synthesized via microwave-induced combustion route. Chem. Eng., J., 156, 471-478 (2010).).
RESULTS AND DISCUSSION
Design of the Experiments and Response Surface Modeling
With respect to the previous sections, 20 different combination treatments were carried out in random order according to a CCD configuration and the results of two responses, zeta potential (mV) and the thermal conductivity ratio were determined experimentally and predicted by the model according to the design. The results are summarized in Table 2.
A second-order polynomial equation was used to find the mathematical relationship between the dependent variables (zeta potential and thermal conductivity ratio) and the set of independent variables. For three factors, the obtained model was expressed as follows:
where y represents the predicted responses, xi and xj are the coded values of the independent variables, b0 is the regression term at the center point, bi are the linear coefficients (main effect), bii are the quadratic coefficients and bij are the two-factor interaction coefficients. Also, for statistical calculation based on CCD, the relation between the dimensionless coded values of the independent variables (xi) and the actual values of them (Xi) are defined as:
where Xi,high and Xi,low are the real values of the independent variables at high and low levels, respectively.
Analysis of Variance (ANOVA)
The ANOVA values for the quadratic regression model obtained from CCRD were employed in the optimization of stability and thermal conductivity; which are respectively tabulated in Tables 3 and 4. With respect to these tables, the F-values of 28.78 and 25.63 implied that the models were statistically significant. There is only a 0.01% chance that model F-values this large could occur due to noise. Also, pvalues less than 0.0500 indicate significant model terms. In the case of the responses in this study, the ranking of the significant model terms for zeta potential and the thermal conductivity ratio were X23 > X1 > X3 > X2 > X22 and X1 > X23 > X2 > X21 > X3, respectively. P-values, which are greater than 0.1, indicate insignificant model terms. The lack-of-fit Fvalues of 2.17 and 0.75 showed that the lack of fit of the models was not statistically important relative to the pure error. The insignificant lack of fit values are good and revealed that the quadratic models are statistically significant for the responses. Consequently, the following second order polynomial regression modeling was performed for the zeta potential (y1) and thermal conductivity ratio (y2) of the nanofluid with coded variables:
The coefficient of determination (R2) expresses the quality of the fit of the polynomial model. The value of this statistical parameter for the zeta potential (R2 = 0.9628) emphasizes that 96.28% of the variability in the response could be explained by the model and only 3.72% of the total variation was not explained by the model. The same interpretation applies to the other response variable. However, a concern with this statistic parameter is that it does not take the numbers of degree of freedom into account for model determination. In other words, it always increases when new variables are added to the model, regardless of whether the additional variable is statistically significant or not. In order to negate this drawback, the adjusted coefficient of determination, R2-Adj, was used to adjust the varying numbers of degrees of freedom in the models. Tables 3 and 4 show that R2 and adjusted-R2 values for the models did not differ, obviously indicating that nonsignificant terms had not been included in the models.
The Predicted-R2 values of the stability and thermal conductivity ratio are 0.7890 and 0.8269, which are in reasonable agreement with the adjusted-R2 of 0.9294 and 0.9210, respectively. A rule of thumb is that the adjusted and predicted R-squared values should be within 0.2 of each other. Otherwise there may be a problem with either the data or the model.
Adequate precision compares the range of predicted values at the design points to the average prediction error. A ratio greater than 4 is desirable to indicate adequate model discrimination. For our quadratic models, the ratios are 19.354 and 16.518 for the responses, indicating that the models give reasonable performance in predictions.
Statistical plots such as the normal probability plot and the studentized residuals versus different independent variables play significant roles in confirming the normal error distribution, evaluating the final model adequacy and independently distributing the observations in a completely randomized design. In this regard, the normal percentage probability plots of the studentized residuals are shown in Figure 3. Regarding this figure, the residual points show that the error distribution was normal and no response transformation was required.
Normal probability plot of residuals for zeta potential (a) and the thermal conductivity ratio (b) of the tin dioxide nanofluid system.
The constant variance assumption for each treatment or factor level and the independence of the errors were checked by plotting the residuals against the different independent variables such as time or run order, factors, and predicted values obtained from the model. As shown in Figure 4, there is no structure such as sequences of positive and negative residuals or megaphone shape. Consequently, the models are correct, the assumptions are satisfying and there was no evidence pointing to possible outliers for both responses. The plots of residuals versus other independent variables were checked (not shown). All figures showed an approximately constant variance over the variable ranges and there was no reason to reject the conclusions.
Plot of studentized residuals versus predicted responses for the zeta potential (a) and thermal conductivity ratio (b) in the tin dioxide nanofluid system.
Effect of Selected Factors on the Zeta Potential of the Nanofluid
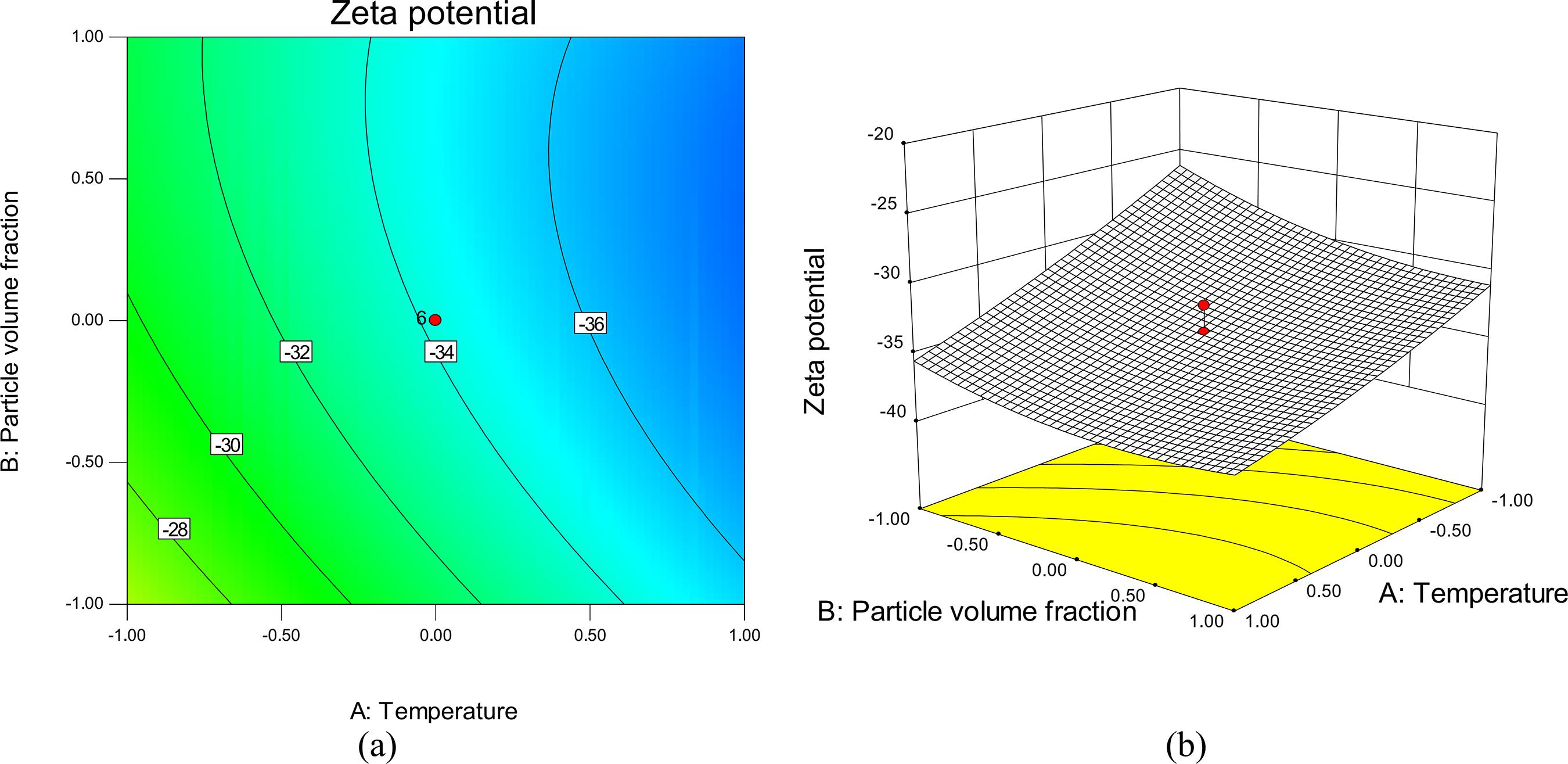
The major challenge in nanofluid systems is the rapid settling of the nanoparticles in fluids. The zeta potential decline is caused by several factors such as nanoparticle clustering, agglomeration and close packing of the dispersed phase. Thus, in order to obtain a better understanding of the results, the threedimensional (3D) response surface plots and contour lines map of the predicted models for zeta potential of the nanofluid are presented in Figures 5-7. The mutual effect of temperature and particle volume fraction at constant solution pH of 7 on stability (zeta potential) of tin dioxide nanofluid is shown in Figure 5. The minimum zeta potential (maximum stability) for tin dioxide nanoparticles is observed at high levels of both selected factors. This minimum is equal to -37.36.
It was observed that the zeta potential decreases (stability increased) upon increasing temperature and particle volume fraction. These facts should take into account that the temperature directly regulates particle kinetic energies, Brownian motion of nanoparticles and finally the coagulation efficiency. Therefore, if the kinetic energy of the particles is lower than their interaction potential, coagulation of two particles occurs after collision. Also, the formation probability of bigger agglomerates increases at low temperatures (Fiedler et al., 2007Fiedler, S. L., Izvekov, S., Violi, A., The effect of temperature on nanoparticle clustering. Carbon, 45, 1786-1794 (2007).; Ghosh et al., 2011Ghosh, M. M., Roy, S., Pabi, S. K., Ghosh, S., A Molecular dynamics-stochastic model for thermal conductivity of nanofluids and its experimental validation. J. Nanosci. Nanotechnol., 10, 196-207 (2011).; Chang et al., 2005Chang, H., Lo, C. H., Tsung, T. T., Cho, Y. Y., Tien, D. C., Chen, L. C., Thai, C. H., Temperature effect on the stability of CuO nanofluids based on measured particle distribution. Key Eng. Mater., 295-296, 51-56 (2005).). This can also be explained by the significant positive quadratic term ( x22 ) and negative linear term (x2) in Eq. (3). According to this equation, the zeta potential (y1) decreased based on a negative linear term and increased based on a positive quadratic term.
It is clear from Figure 5 that the stability increases upon increasing SnO2 concentration. This behavior could be explained by two effects. First of all, the viscosity of a nanofluid is higher than that of its base fluid and increases with an increase in the particle volume concentration (Goharshadi et al., 2013Goharshadi, E. K., Ahmadzadeh, H., Samiee, S., Hadadian, M., Nanofluids for Heat transfer enhancement-a review. Phys. Chem. Res., 1(1), 1-33 (2013).). Secondly, due to the high surface area and surface activity, nanoparticles have the tendency to aggregate. The use of efficient surfactant is another key method to enhance the stability of nanoparticles in the base fluid (Yu et al., 2012Yu, W., Xie, H., A review on nanofluids: Preparation stability mechanisms and application. J Nanomater, 2012(1), 1-17 (2012).). Surfactants play a very crucial role in nanofluid systems. The concentration of the surfactant has a positive effect on the dynamic viscosity of nanofluids and prevents the nanoparticle agglomeration due to the increase of electrostatic repulsion between the suspended particles. Consequently, adding surfactant significantly minimizes particle aggregation and enhances the dispersion behavior (Goharshadi et al., 2013Goharshadi, E. K., Ahmadzadeh, H., Samiee, S., Hadadian, M., Nanofluids for Heat transfer enhancement-a review. Phys. Chem. Res., 1(1), 1-33 (2013).; Hwang et al., 2007Hwang, Y., Lee, J. K., Lee, C. H., Jung, Y. M., Cheong, S. I., Lee, C. G., Ku, B. C., Jang, S. P., Stability and thermal conductivity characteristics of nanofluids. Thermochimica Acta, 455, 70-74 (2007).; Hwang et al., 2008Hwang, Y., Lee, J. K., Jeong, Y. M., Cheong, S. I., Ahn, Y. C., Kim, S. H., Production and dispersion stability of nanoparticles in nanofluids. Powder Technol., 186, 145-153 (2008).). Although the increase in nanoparticle concentration improves stability, the agglomeration is more obvious at concentrations over 5% (Pirahmadian and Ebrahimi, 2012Pirahmadian, M. H., Ebrahimi, A., Theoretical Investigation heat transfer mechanisms in nanofluids and the effects of clustering on thermal conductivity. Int. J. Biosci. Biochem. Bioinform., 2(2), 90-94 (2012).). This can also be explained by the significant quadratic term x22 in Eq. (3).
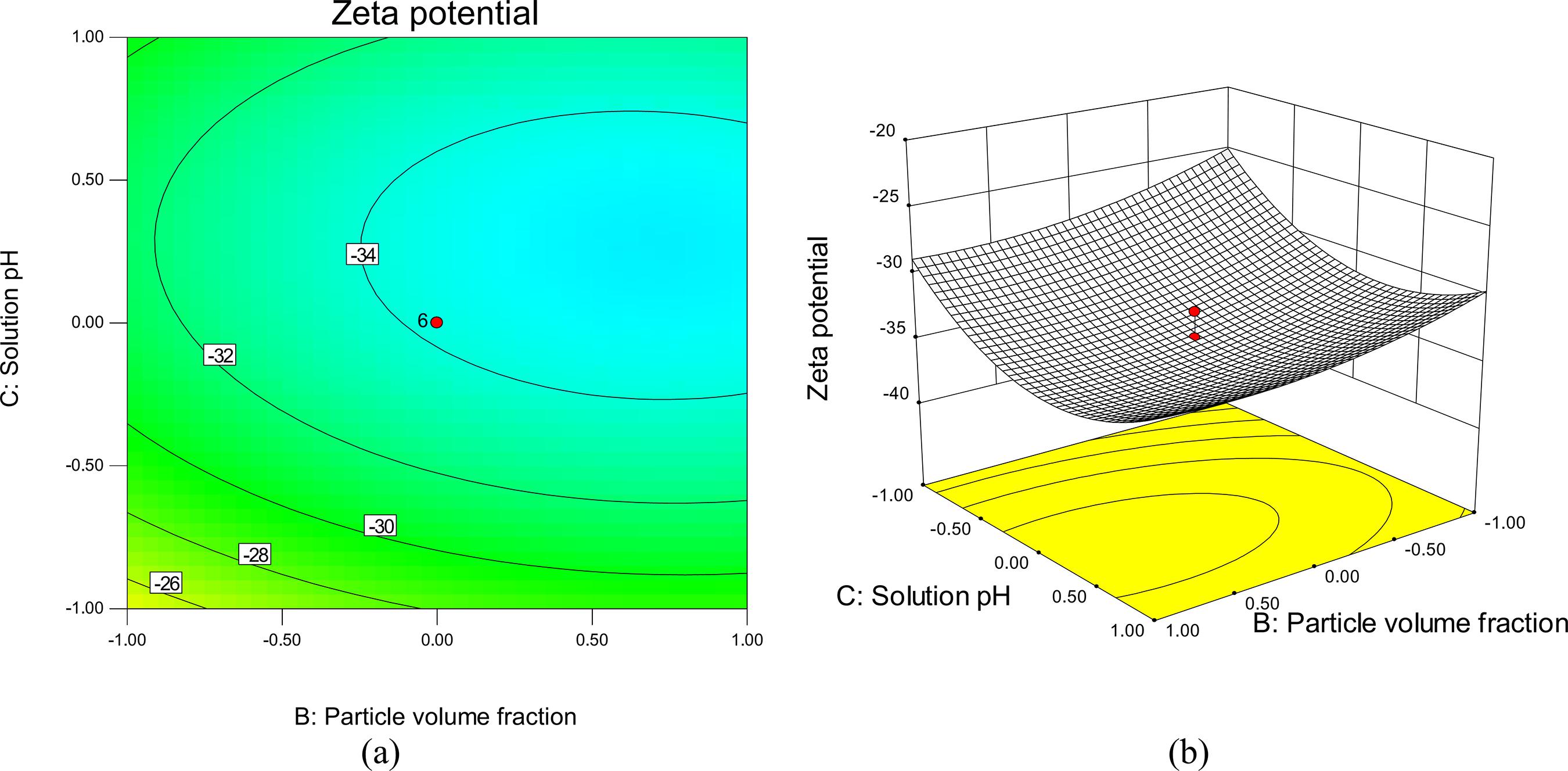
Figure 6 shows the effect of solution pH versus temperature at a constant nanoparticle concentration of 3% by volume. The maximum response zone of stability is observed at pH values of 7 to 8.25 at each temperature level. This illustrates that increasing the pH up to 7-8 will enhance stability. This behavior is due to the fact that the stability of a nanofluid is related to its electrokinetic properties. At the isoelectric point (IEP), the repulsive forces between SnO2 nanoparticles tend towards zero and nanoparticles will coagulate together at this pH value.
The hydration forces between nanoparticles increase as the pH of the solution departs from the IEP, which results in the enhanced mobility of nanoparticles in the suspension and the colloidal particles become more stable (Habibzadeh et al., 2010Habibzadeh, S., Kazemi-Beydokhti, A., Khodadadi, A. A., Mortazavi, Y., Omanovic, S., Shariat-Niassar, M., Stability and thermal conductivity of nanofluids of tin dioxide synthesized via microwave-induced combustion route. Chem. Eng., J., 156, 471-478 (2010).; Goharshadi et al., 2013Goharshadi, E. K., Ahmadzadeh, H., Samiee, S., Hadadian, M., Nanofluids for Heat transfer enhancement-a review. Phys. Chem. Res., 1(1), 1-33 (2013).). At high and low levels of solution pH, stability has a tendency to decrease. Theoretically, this may be attributed to the decrease of the surface charge. As a result, a weakly repulsive double layer force is generated
Response surface and contour plots showing the mutual effect of temperature and particle volume fraction on zeta potential while the other factor was kept constant at the center point (X3=7).
Response surface and contour plots showing the mutual effect of temperature and pH on zeta potential while the other factor was kept constant at the center point (X2=3% by volume).
The interaction effect of particle volume fraction and solution pH at a constant temperature of 45 °C on zeta potential is depicted in Figure 7. As shown in this figure, there is an enough curvature in this plot and the response surface is moderately nonlinear. In order to capture the curvature of the response in the design space, significant quadratic terms such as x22 and x32 were taken into account in Eq. (3). The same interpretation is applied for pH and the concentration of nanoparticles on the stability of the nanofluid. The contour plot shows that the process is more sensitive to a change in pH than in particle volume fraction. The optimum is close to the pH of 8 and a particle volume fraction of 3.5% by volume.
Response surface and contour plots showing the mutual effect of particle volume fraction and pH on zeta potential while the other factor was kept constant at the center point (X1=45 °C).
Effect of Selected Factors on the Thermal Conductivity Ratio
Previous experimental studies showed that the thermal conductivity enhancement of nanofluids depends on several mechanisms such as Brownian motion of the nanoparticles, clustering of the nanoparticles and liquid layering around the nanoparticles (Pirahmadian and Ebrahimi, 2012Pirahmadian, M. H., Ebrahimi, A., Theoretical Investigation heat transfer mechanisms in nanofluids and the effects of clustering on thermal conductivity. Int. J. Biosci. Biochem. Bioinform., 2(2), 90-94 (2012).; Ghadimi et al., 2011Ghadimi, A., Saidur, R., Metselaar, H. S. C., A Review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transfer, 54, 4051-4068 (2011).). These phenomena can also be described by several significant factors such as temperature, particle volume fraction, pH of the nanofluid, etc. In this regard, the 3D response surface plots and contour line map of the predicted models for the thermal conductivity ratio of nanofluid are presented in Figures 8-10.
Response surface and contour plots showing the mutual effect of temperature and particle volume fraction on the thermal conductivity ratio while the third factor was kept constant at the center point (X3=7).
Response surface and contour plots showing the mutual effect of temperature and pH on the thermal conductivity ratio while the third factor was kept constant at the center point (X2=3% volume).
Response surface and contour plots showing the mutual effect of particle volume fraction and pH on the thermal conductivity ratio while the third factor was kept constant at the center point (X1=45 °C).
Figure 8 demonstrates the variations in the thermal conductivity ratio in terms of the temperature and particle volume fraction variables while the solution pH was kept constant at the center point. By considering this figure, increasing the temperature from 35 to 55 °C increases the thermal conductivity to 7.47% and 6.44% at the high level and the low level of the particle volume fraction, respectively. These enhancements in thermal conductivity can be adequately explained by kinetic theory; Brownian movement (stochastic motion of molecules and nanoparticles) increases with the increase of the nanofluid's bulk temperature. Consequently, these particles are able to transfer more energy from one place to another per time unit. On the other hand, these enhancements are due to a reduction in the clustering effect which is intensified by an increase in temperature (Das et al., 2003bDas, S. K., Putta, N., Thiesen, P., Roetzel, W., Temperature dependence of thermal conductivity enhancement for nanofluid. ASME Trans. J. Heat Transf., 125, 567-574 (2003b).).
Most experimental observations of nanofluid systems show that the thermal conductivity ratio increases remarkably with the increase of particle volume fraction. This behavior is also evident in Figures 8 and 10. This phenomenon is attributed to the fact that the collision of nanoparticles with each other is increased by increasing the nanoparticle concentration. Although the probability of nanoparticle agglomeration increases with increasing particle volume fraction, dispersing agents such as SDS reduce the van der Waals forces and improve nanoparticle dispersion.
It was also observed that the rate of change of the thermal conductivity with temperature and particle volume fraction was dependent on the pH value, as shown in Figures 9 and 10, respectively. This is due to the fact that the pH value strongly influences the electrostatic charge of the particle surface. The thermal conductivity ratio increases with pH, reaches a maximum close to the isoelectric point and decreases as the pH increases further.
At the optimum value of the pH (approximately between 8 and 9) for maximum thermal conductivity enhancement, the surface charge of nanoparticles increases, which creates a high electrostatic repulsion between nanoparticles. Consequently, the mobility of tin dioxide nanoparticles is enhanced and severe clustering and agglomeration of the nanoparticles are prevented (Shanbedi et al., 2014Shanbedi, M., Zeinali Heris, S., Amiri, A., Adyani, S., Alizadeh, M., Baniadam, M., Optimization of thermal efficiency of a two-phase closed thermosyphon using active learning on the human algorithm interaction. Numer. Heat Transfer-Part A: Applications, 66(8), 947-962, (2014).; Goharshadi et al., 2013Goharshadi, E. K., Ahmadzadeh, H., Samiee, S., Hadadian, M., Nanofluids for Heat transfer enhancement-a review. Phys. Chem. Res., 1(1), 1-33 (2013).; Ranakoti Irtisha et al., 2012Ranakoti Irtisha, G., Dewangan, S., Kosti, S., Nemade, R., Heat Transfer Enhancement by Nano Fluids. Convective Heat Mass Transfer, ME642, 1-9 (2012).; Xian-Ju and Xin-Fang, 2009Xian-Ju, W., Xin-Fang, L., Influence of pH on nanofluids’ viscosity and thermal conductivity. Chin. Phys. Lett., 26(5), 1-4 (2009).).
Optimization of the Operational Conditions
The final optimum experimental results based on RSM strategy were calculated by the software to determine the optimum settings for the factors. The optimal experimental conditions based on the coded factors and the responses were carried out by minimizing the zeta potential and maximizing thermal conductivity ratio and are reported in Table 5. With respect to this table, all three factors were limited to their lower and upper coded values. The default is for both responses to be equally important in a setting of 3 pluses (+++). The optimal process conditions determined by the CCRD method based on the actual values of the factors are as follows: X1 = 55 °C, X2 = 3.36% by volume and X3 = 8.62; in these conditions, a zeta potential of -38.22 mV was obtained in result 1. The value of 1.23 was obtained for the maximum thermal conductivity ratio at X1 = 54.4 °C, X2 = 3.98% by volume and X3 = 8.84 in result 2.
Optimum values of the design criteria for the zeta potential and thermal conductivity ratio for the tin dioxide nanofluid.
Under the optimal experimental conditions for both responses, a zeta potential of -37.98 mV and thermal conductivity ratio of 1.23 were determined at X1 = 55 °C, X2 = 3.81% by volume and X3 = 8.6 in result 3.
Artificial Neural Networks Modeling
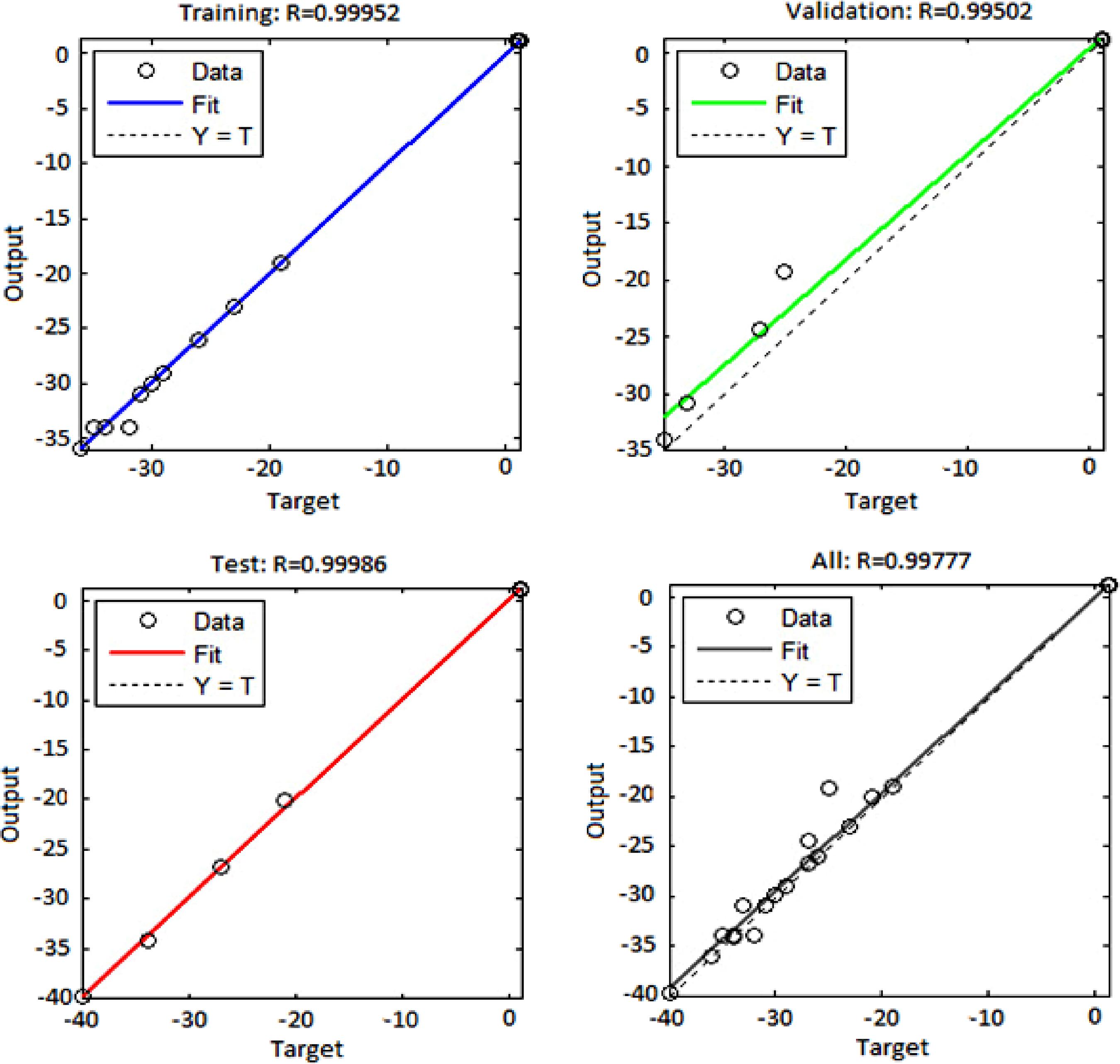
Figure 11 shows the regression plots for the output with respect to training, validation, and test data. With respect to this figure, the output tracks the targets quite well and the R-value is over 0.995. Consequently, neural networks are able to predict the present nanofluid system.
The ability of the ANN model and its accuracy for this system are shown by the comparison between the values predicted by the ANN model and experimental data that were not used in training of the ANN, as presented in Figure 12. The proximity of the points to the diagonal line in Figure 12 indicates that the ANN provides results very close to the experimental measurements and confirms the accuracy of the ANN model.
Correlation between experimental and predicted values of (a) zeta potential and (b) thermal conductivity ratio.
To show the accuracy of the model, the absolute average relative error (AARE) and standard deviation (Std. Dev.) for N data were calculated as follow (Gheshlaghi, 2007Gheshlaghi, R., Optimization of Recombinant Protein Production by a Fungal Host. Ph.D. Thesis, Waterloo, Ontario, Canada (2007).):
Table 6 lists the %AARE and %Std. Dev. values for the zeta potential and thermal conductivity ratio. Because the AARE values for both parameters are very small and close to zero, we can conclude that the ANN model is suitable for the prediction of this nanofluid system and that the prediction values are reliable (Rahmanian et al., 2011Rahmanian, B., Pakizeh, M., Mansoori, S. A. A., Abedini, R., Application of Experimental design approach and Artificial Neural Network (ANN) for the determination of potential micellar-enhanced ultrafiltration process. J. Hazard Mater. 187, 67-74 (2011).).
CONCLUSION
The performance of the nanofluid system was modeled and expressed in terms of the stability and thermal conductivity content of the nanoparticles. In this regard, the effect of varying temperature, particle volume fraction and the pH of solution were investigated using RSM and ANN methods. The results clearly show that CCRD and the ANN model can be used for the modeling of the SnO2 nanofluid system. ANOVA analysis indicated that there is significant curvature in the design space. Consequently, the quadratic models were statistically fitted to capture the curvature using CCRD. A multilayer neural network was also used, which is effective for finding complex non-linear relationships. This mathematical model was found to be a reliable predictive tool with an excellent accuracy, with AARE of ±0.872% and ±0.376% in comparison with experimental values for the zeta potential and thermal conductivity ratio, respectively. Finally, the optimization demonstrated that a temperature of 55 °C, particle volume fraction of 3.81% volume and pH=8.6, provided the maximum stability and thermal conductivity enhancement.
NOMENCLATURE
Greek Symbols
ACKNOWLEDGEMENTS
The authors would like to thank the Iran Nano Technology Initiative Council for financial support of this project.
REFERENCES
- Akhtar, M., Five-factor central composite designs robust to a pair of missing observations. J. Res. Sci., 12(2), 105-115 (2001).
- Chang, H., Lo, C. H., Tsung, T. T., Cho, Y. Y., Tien, D. C., Chen, L. C., Thai, C. H., Temperature effect on the stability of CuO nanofluids based on measured particle distribution. Key Eng. Mater., 295-296, 51-56 (2005).
- Das, S. K., Choi, S. U. S., Yu, W., Pradeep, T., Nanofluids: Science and Technology. John Wiley & Sons, Hoboken, New Jersey (2008).
- Das, S. K., Putra, N., Thiesen, P., Roetzel, W., Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat Transfer, 125, 567-574 (2003a).
- Das, S. K., Putta, N., Thiesen, P., Roetzel, W., Temperature dependence of thermal conductivity enhancement for nanofluid. ASME Trans. J. Heat Transf., 125, 567-574 (2003b).
- Eastman, J. A., Choi, S. U. S., Li, S., Yu, W., Thompson, L. J., Anomalously increased effective thermal conductivities of ethylene glycolbased nanofluids containing copper nanoparticles. Appl. Phys. Lett., 78, 718-720 (2001).
- Evans, W., Prasher, R., Fish, J., Meakin, P., Phelan, P., Keblinski, P., Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids. Int. J. Heat Mass Transfer, 51, 1431-1438 (2008).
- Fiedler, S. L., Izvekov, S., Violi, A., The effect of temperature on nanoparticle clustering. Carbon, 45, 1786-1794 (2007).
- Ghadimi, A., Saidur, R., Metselaar, H. S. C., A Review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transfer, 54, 4051-4068 (2011).
- Gheshlaghi, R., Optimization of Recombinant Protein Production by a Fungal Host. Ph.D. Thesis, Waterloo, Ontario, Canada (2007).
- Gheshlaghi, R., Scharer, J. M., Moo-Young, M., Douglas, P. L., Application of statistical design for the optimization of amino acid separation by reverse-phase HPLC. Anal. Biochem., 383, 93-102 (2008).
- Ghosh, M. M., Roy, S., Pabi, S. K., Ghosh, S., A Molecular dynamics-stochastic model for thermal conductivity of nanofluids and its experimental validation. J. Nanosci. Nanotechnol., 10, 196-207 (2011).
- Goharshadi, E. K., Ahmadzadeh, H., Samiee, S., Hadadian, M., Nanofluids for Heat transfer enhancement-a review. Phys. Chem. Res., 1(1), 1-33 (2013).
- Habibzadeh, S., Kazemi-Beydokhti, A., Khodadadi, A. A., Mortazavi, Y., Omanovic, S., Shariat-Niassar, M., Stability and thermal conductivity of nanofluids of tin dioxide synthesized via microwave-induced combustion route. Chem. Eng., J., 156, 471-478 (2010).
- Hwang, Y. J., Ahn, Y. C., Shin, H. S., Lee, C. G., Kim, G. T., Park, H. S., Lee, J. K., Investigation on characteristics of thermal conductivity enhancement of nanofluids. Curr. Appl. Phys., 6, 1068-1071 (2006).
- Hwang, Y., Lee, J. K., Jeong, Y. M., Cheong, S. I., Ahn, Y. C., Kim, S. H., Production and dispersion stability of nanoparticles in nanofluids. Powder Technol., 186, 145-153 (2008).
- Hwang, Y., Lee, J. K., Lee, C. H., Jung, Y. M., Cheong, S. I., Lee, C. G., Ku, B. C., Jang, S. P., Stability and thermal conductivity characteristics of nanofluids. Thermochimica Acta, 455, 70-74 (2007).
- Jiang, W., Wang, L. Q., Copper nanofluids: Synthesis and thermal conductivity. Curr. Nanosci., 6, 512519 (2010).
- Kazemi-Beydokhti, A., Azizi-Namaghi, H., Zeinali Heris, S., Identification of the key variables on thermal conductivity of CuO nanofluid by a fractional factorial design approach. Numer. Heat Transfer-Part B, Fundamentals, 64, 480-495 (2013).
- Lee, S., Choi, S. U. S., Li, S., Eastman, J. A., Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transf., 121, 280-289 (1999).
- Molana, M. and Banooni, S., Investigation of heat transfer processes involved liquid impingement jets: A review. Braz. J. Chem. Eng., 30 (3), 413435 (2013).
- Montgomery, D. C., Runger, G. C., Applied Statistics and Probability for Engineers. 3rd Ed., John Wiley & Sons, New York, U.S.A (2003).
- Murshed, S. M. S., Leong, K. C., Yang, C., Enhanced thermal conductivity of TiO2–water based nanofluids. Int. J. Therm. Sci., 44, 367-373 (2005).
- Pirahmadian, M. H., Ebrahimi, A., Theoretical Investigation heat transfer mechanisms in nanofluids and the effects of clustering on thermal conductivity. Int. J. Biosci. Biochem. Bioinform., 2(2), 90-94 (2012).
- Proust, M., Design of Experiments Guide. SAS Institute Inc., Cary, NC, USA (2010).
- Rahmanian, B., Pakizeh, M., Mansoori, S. A. A., Abedini, R., Application of Experimental design approach and Artificial Neural Network (ANN) for the determination of potential micellar-enhanced ultrafiltration process. J. Hazard Mater. 187, 67-74 (2011).
- Ranakoti Irtisha, G., Dewangan, S., Kosti, S., Nemade, R., Heat Transfer Enhancement by Nano Fluids. Convective Heat Mass Transfer, ME642, 1-9 (2012).
- Salehi, H., S. Zeinali Heris, H., Koolivand Salooki, M., Noei, S. H., Designing a neural network for closed thermosyphon with nanofluid using genetic algorithm. Braz. J. Chem. Eng., 28(1), 157168 (2011).
- Salehi, H., Zeinali Heris, S., Esfandyari, M., Koolivand, M., Nero-fuzzy modeling of the convection heat transfer coefficient for the nanofluid. Heat Mass Transfer, 49, 575-583 (2013).
- Shanbedi, M., Jafari, D., Amiri, A., Zeinali Heris, S., Baniadam, M., Prediction of temperature performance of a two-phase closed thermosyphon using artificial neural network. Heat Mass Transfer, 49, 65-73 (2013).
- Shanbedi, M., Zeinali Heris, S., Amiri, A., Adyani, S., Alizadeh, M., Baniadam, M., Optimization of thermal efficiency of a two-phase closed thermosyphon using active learning on the human algorithm interaction. Numer. Heat Transfer-Part A: Applications, 66(8), 947-962, (2014).
- Tucknott, R., Yaliraki, S. N., Aggregation properties of carbon nanotubes at interfaces. Chem. Phys., 281, 455-463 (2002).
- Wang, X. Q., Mujumdar A. S., A review on nanofluids - part II: Experiments and applications. Braz. J. Chem. Eng., 25(4), 631-648 (2008a).
- Wang, X. Q., Mujumdar, A. S., A review on nanofluids – part I: Theoretical and numerical investigations. Braz. J. Chem. Eng., 25(4), 613-630 (2008b).
- Xian-Ju, W., Xin-Fang, L., Influence of pH on nanofluids’ viscosity and thermal conductivity. Chin. Phys. Lett., 26(5), 1-4 (2009).
- Yousefi, F., Karimi, H., Papari, M. M., Modeling viscosity of nanofluids using diffusional neural networks. J. Mol. Liq., 175, 85-90 (2012).
- Yu, W., Xie, H., A review on nanofluids: Preparation stability mechanisms and application. J Nanomater, 2012(1), 1-17 (2012).
- Zeinali Heris, S., Nasr Esfahany, M., Etemad, S. Gh., Numerical investigation of nanofluid laminar convective heat transfer through a circular tube. Numer. Heat Transfer-Part A: Applications, 52, 1043-1058 (2007).
Publication Dates
-
Publication in this collection
Oct-Dec 2015
History
-
Received
24 May 2014 -
Reviewed
30 Nov 2014 -
Accepted
09 Jan 2015