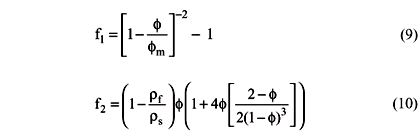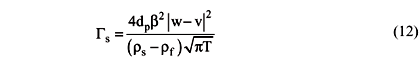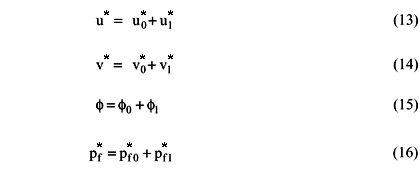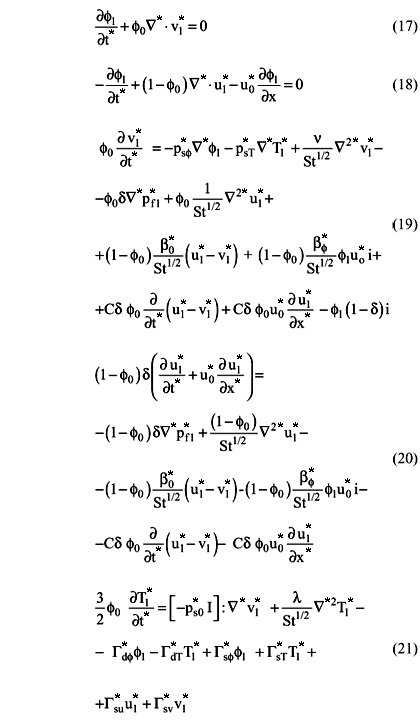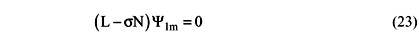A novel mechanism for bubble formation in fluidized systems: the effects of granular temperature on the stability in fluidization

TRANSPORT PHENOMENA AND UNITY OPERATION

A novel mechanism for bubble formation in fluidized systems: the effects of granular temperature on the stability in fluidization

A. M. S. Costa; M. L. de Souza-Santos^*

Faculty of Mechanical Engineering, Department of Energy, State University of Campinas, Unicamp, PO Box 6122, CEP 13083-970, Phone: +(55) (19) 3788-3278, Campinas - SP, Brazil. E-mail: [e-mail]

ABSTRACT

This work contains a novel approach for the study of stability in fluidized systems. It includes the influence of solid particle kinetic energy variations, which are known as granular temperature. The stability is verified by the temporal evolution of bed fluid-dynamics properties (solid volumetric fraction, fluid velocity, solid particles velocity) after small perturbations. The bed is stable when the amplitudes of perturbations decrease with time. The work departs from the mass and momentum continuity equations for the solid and fluid phase, as proposed by Anderson and Jackson (1968). Those are complemented by an equation describing the energy balance from the point of view of granular temperature. Then, a linear approximation for the equations after the introduction of small magnitude perturbations is obtained. The application of harmonic solutions allows arriving to the temporal description of the perturbations. Results show the occurrence of instabilities on the direction transverse to gravity. This cannot be observed by previous approaches (Anderson and Jackson, 1968, 1969; Homsy et al., 1980; Liu, 1982). The present work also suggests a new mechanism for the formation of bubbles in fluidized systems. The parametric influence of the model on the stability of fluidized systems is also verified.

Keywords: fluidized beds, stability, granular temperature, linear analysis.

INTRODUCTION

The first works on mathematical modeling on stability for fluidized systems appeared in the sixties. Applying the continuum conservation equations and linear stability analysis, Jackson (1963) predicted instabilities in all situations, even when very small perturbations were imposed to uniform fluidized beds. Afterward, Anderson and Jackson (1968, 1969) refined the initial modeling adding the solids stress tensor in the momentum equations. Their results presented qualitative agreement against experimental verifications and allowed to estimate representative values for parameters such as solid pressure, solid viscosity and special interaction terms between various phases. Using a more accurate data acquisition system, Homsy et al (1980) developed a similar work of the previously carried by Anderson and Jackson (1969).

Subsequently, experiments by Didwania and Homsy (1981) applied to larger beds, were able to clearly depict the instability dynamics. They verified the formation of wavy structures after the growth and saturation of vertical instability amplitudes. In addition, if larger fluid flow rates were imposed, these geometric configurations were substituted by the turbulent state followed by the formation of bubbles.

Batchelor (1988) investigated the linear stability of fluidized systems using a new formulation for the conservation equations. Similarly to the results by previous authors, the agreement with experiments relied on estimation of parameters.

In order to clarify the complex dynamics of fluidized systems, several works were developed using a non-linear stability analysis of the conservation equations for the phases (Liu, 1983; Needham and Merkin, 1986; Ganser and Drew, 1990; Goz, 1993; Anderson et al, 1995; Glasser et al, 1996). However, these models failed to correctly predict the experimentally observed changes in fluid dynamics.

This work presents a new approach to the study of the stability of fluidized systems. It includes the kinetic energy variations of solid particles, known as granular temperature.

CONSERVATION EQUATIONS

The classical approach for the theoretical investigation of fluidization dynamics uses the two-fluid model (Ishii, 1975). According to Anderson and Jackson (1967), that model leads to the following forms for the mass and momentum conservation equations:

Equations (1) and (2) assume the incompressibility of the phases and no mass exchange between them. The left sides of Equations (3) and (4) represent the inertial forces on the fluid and solid phases, respectively. The terms inside the first brackets at the right side of Eq. (4) represent the actions of the solid phase tensors. Excluding those and the last term, which represents the gravitational action, the remaining at the right side represent the interaction with the fluid phase. Similar terms can be identified in the Equation 3 concerning the fluid phase.

THE GRANULAR TEMPERATURE

The concept of granular temperature was first applied by a group of researches (Savage and Jeffrey, 1981; Haff, 1983, Jenkins and Richman, 1986) for the modeling of flows where solid particles were present. Its use for the study of the stability of fluidized systems is relatively recent (Buyevich and Kapbasov, 1994; Koch and Sangani, 1999, Didwania, 1999; Didwania and Costa, 2000). The idea of granular temperature follows an analogy between the flow of particulate materials and the molecules movement, as described by the gas kinetic theory. It is defined by the kinetic energy associated with the velocity fluctuations of the solid particles, or:

In addition, using the previous analogy, it is defined the following solid phase properties (Costa, 2002):

where

Equation (8) represents the term of energy dissipation according to the granular temperature balance given by:

Finally, applying and extension of the results obtained by Koch (1990), the following expression is proposed for the source term:

DIMENSIONLESS EQUATIONS AND LINEAR ANALYSIS

Using the particle diameter d_p as characteristic length and as characteristic velocity, it is possible to write the above set of equations in dimensionless form.

Next, let be the dimensionless set perturbations given by:

Here, the functions u₁, v₁, e₁, p_f1 are supposed to have low magnitude, if compared with the base state functions. It should be noticed that all second and higher order terms are neglected. Applying the above perturbations into the dimensionless forms of Equations (1) to (4), the following set of linear partial differential equations can be written:

The stability is investigated defining harmonic perturbations given by Y₁ = Y_1me^ik.x*+st, where

The following matrix equation can be obtained by substituting Equation (22) into Equations (17) to (21):

The existence of non-trivial solutions can be guaranteed if determinant of the term between parentheses in Equation (23) is equal to zero. This leads to a fifth order polynomial in s with roots given by:

RESULTS

Figure 1 shows the behavior of the maximum growth rate s_rmax as function of Stokes number and the wave propagation direction.

The previous figure indicates that maximum values occur for waves propagating in the horizontal direction, i.e., q = 0^o and those values increase with the Stokes number. The results also suggest stability for waves propagating close to the vertical direction for Stokes numbers between 10 and 10⁴.

Figure 2 shows those maximum values of frequency s_imax occur close to the vertical direction. It can be verified that frequency vanishes at the horizontal direction, which indicates a non-oscillating temporal characteristic. Additionally, it has been shown that it increases with the Stokes number.

At a given instant, Figure 3 illustrates the surface contour of an instability, which amplitude growth factor at horizontal direction is larger than at vertical direction. That figure suggests the possibility of formation of bubble-like structures when the growth factor in the horizontal direction differs from zero. This agrees with the experimental observations by Homsy et al (1980). A comparison with their observations suggests that during the bubble formation, a transition from the isothermal mode to the non-isothermal mode takes place. The first mode does not consider the granular temperature effects, while the second does.

For the non-isothermal case, it was also verified (Costa, 2002) that:

1) The effects of fluid and solid density ratio agree with experimental evidences, which show greater stability of liquid-fluidized systems if compared with gas-fluidized ones.

2) A decrease for the coefficient n leads to increases on instabilities.

3) Decreases in minimum fluidization void fraction leads to greater stability.

4) Decreased on particle thermal conductivity leads to larger instabilities.

5) In agreement with the isothermal results by Anderson e Jackson (1968), it has been shown that the following factors contribute to bed stability:

6) Higher solid phase viscosity.

7) Higher derivatives of solid pressure against solid fraction (or fraction of bed volume occupied by the solid phase).

8) On the other hand, if the granular temperature is introduced in the mathematical treatment, the following effects have been verified:

9) Increases in the solid pressure, as well its derivative against the granular temperature, improve bed stability.

10) Increases in the net source term derivative against the granular temperature also improve bed stability.

Increases in the net source term derivative against the solid fraction decrease bed stability.

Figure 4 shows a comparison between the theoretical results for the maximum wave number and the experiments by Homsy et al. (1980) in a solid-liquid fluidized bed. It suggests that better agreement can be obtained by parameter adjusting. It should be stressed the parsimony of valuable experimental results in the literature for comparison with the theoretical predictions.

CONCLUSIONS

The introduction of granular temperature showed that fluidized beds might become unstable if disturbances are imposed at direction transverse to gravity. This suggests a new explanation for the secondary instabilities experimentally observed in fluidized beds.

The present treatment can be further improved as long more experimental observations regarding instability propagation is available.

ACKNOWLEDGEMENTS

This work was financially supported by FAPESP foundation.

NOMENCLATURE

C

virtual mass coefficient (=0.5)

d_p

particle diameter

[m] g local gravity acceleration [m s^-2] g vector of gravity acceleration [m s^-2] i, j, k unit Cartesian vectors I identity matrix k wave number vector L

matrix defined by (23)

N matrix defined by (23) n exponent from the Richardson and Zaki equation p pressure [N m^-2] St Stokes number t time [s] T granular temperature [m² s^-2] u

local average velocity vector for the fluid phase

[m s^-1] u₀ interstitial velocity, related with the terminal velocity by Richardson and Zaki (1954) equation [m s^-1] v

local average velocity vector for the solid phase

[m s^-1] v_t terminal velocity in the Stokes range [m s^-1] x vertical coordinate [m] x

position vector

[m] y

horizontal coordinate

[m] w velocity vector (= u - u_mf)

Greeks Letters

G_s source term [m² s^-3] G_d dissipative term [m² s^-3] f solids volumetric fraction r density [kg m^-3] n m_s / m_f ratio d r_s / r_f ratio m

dynamic viscosity

[kg m^-1 s^-1] b coefficient for the phases interaction parameters [kg m^-3 s^-1] l ration k

thermal conductivity

[kg m^-1 s^-1] s complex parameter whose imaginary and real parts, s_r and s_i , defines respectively the growth factor for amplitude and temporal frequency. q

angle with respect to the horizontal direction.

s_rmax maximum value for the s_r part in the wave number domain s_imax respective imaginary s_i part corresponding to s_rmax Superscript * dimensionless value Subscript II

direction parallel to gravity

^ direction perpendicular to gravity 0 undisturbed state 1 disturbed state m maximum packing condition f fluid phase mf minimum fluidization condition s

solid phase

f derivative with respect to the solids fraction in the undisturbed state T derivative with respect to the granular temperature in the undisturbed state.

Received: ;

Accepted:

• Anderson, K., Sundaresan, S. and Jackson, R., Instabilities and the Formation of Bubbles in Fluidized Beds, Journal of Fluid Mechanics, vol. 303, pp. 327-366, 1995.
• Anderson, T.B. and Jackson, R., A Fluid Mechanical Description of Fluidized Beds: Equations of Motion, Industrial Engineering Chemical Fundamentals, 6, pp. 527-539, 1967.
• Anderson, T.B. and Jackson, R., Fluid Mechanical Description of fluidized beds: Stability of the state of uniform fluidization, Industrial Engineering Chemical Fundamentals, vol.7, pp.12-21, 1968.
• Anderson, T.B. and Jackson, R., A Fluid Mechanical Description of Fluidized Beds: Comparison of Theory and Experiment, Industrial Engineering Chemical Fundamentals, vol. 8, pp.137-144, 1969.
• Batchelor, G.K., A New Theory of the Instability of a Uniform Fluidized Bed, Journal of Fluid Mechanics, vol. 193, pp.75-110, 1988.
• Buyevich, Y. A. and Kapbasov, S. K., Random Fluctuations in a Fluidized Bed, Chemical Engineering Science, vol. 49, pp. 1229-1243, 1994.
• Costa, A.M.S. (2002), Fluidization Stability: The Effect of Granular Temperature Inclusion (Estabilidade em fluidizaçăo: O efeito da inclusăo da temperatura granular) Ph.D. Thesis presented to the Faculty of Mechanical Engineering, UNICAMP State University of Campinas, SP, Brasil, 170pp., 2002.
• Didwania, A.K. and Costa, A.M.S., Effect of Particle Velocity Fluctuations on the Stability of Fluidized Beds, Proceedings of the Forum on Particle Technology, AIChE Annual Meeting. 12-17 Nov 2000, Los Angeles, 2000.
• Didwania, A.K. and Homsy, G.M., Flow Regimes and Flow Transitions in Liquid fluidized Beds, International Journal of Multiphase Flow, 7, pp. 563-580, 1981.
• Didwnia, A.K., Packed-to-Fluidized Bed Transition and Origin of Particle-free regions, Proceedings of the IUTAM Symposium Theoretical and Numerical Methods in Continuum Mechanics of Porous Materials, Kluwer Press, Stuttgart, 1999.
• Ganser, G.H. and Drew, D.A., Nonlinear Stability Analysis of a Uniformly Fluidized Bed, International Journal of Multiphase flow, vol. 16, n.3, pp. 447-460, 1990.
• Glasser, B.J., Kevrekidis, I.G. and Sundaresan, S., One- and Two-dimensional Travelling Wave solutions in Gas-fluidized Beds, Journal of Fluid Mechanics, vol. 306, pp. 183-221, 1996.
• Goz, M.F., Bifurcation of Plane Voidage Waves in Fluidized Beds, Physica D, vol. 65, pp. 319-351, 1993.
• Haff, p. k., Grain Flow as a Fluid-mechanical, Journal of Fluid Mechanics, vol. 134, pp. 401-430, 1983.
• Homsy, G.M., El-Kaissy, M.M. and Didiwania, A., Instability Waves and the Origin of Bubbles in Fluidized Beds-II: Comparison with Theory, International Journal of Multiphase Flow, vol. 6., pp. 305-318, 1980.
• Ishi, M., Thermo-Fluid Dynamic Theory of Two Phase Flow. Eyrolles, Paris, 1975.
• Jackson, R., The Mechanics of Fluidized Beds: Part I: The Stability of the State of Uniform Fluidization, Transactions Institute of Chemical Engineers, 41, pp. 13-21, 1963.
• Jenkins, J. T. and Richman, M. W., Boundary Conditions for Planes Flows of Smooth Nearly Elastic, Circular Disks, Journal of Fluid Mechanics, vol. 171, pp. 53-69, 1986.
• Koch, d. l., Kinetic Theory for a Monodisperse Gas-Solid Suspension. Physics Fluids A, vol. 2, pp. 1711-1723, 1990.
• Koch, d. l. and Sangani, A.S., Particle Pressure and Marginal Stability Limits for a Homogeneous Monodisperse Gas-fluidized Bed: Kinetic Theory and Numerical Simulations, Journal of Fluid Mechanics, vol. 400, pp. 229-263, 1999.
• Liu, J. T. C., Note on a Wave Hierarchy Interpretation of Fluidized Bed Instabilities. Proceedings of the Royal Society London: A, vol. 380, pp. 229-239, 1982
• Liu, J. T. C., Nonlinear Unstable Wave Disturbances in Fluidized Beds. Proceedings of the Royal Society London: A, vol. 389, pp. 331-347, 1983.
• Needhan, D. J. and Merkin, J. H., The Existence and Stability of Quasi-steady Periodic Voidage Waves in a Fluidized Bed, Journal of Applied Mathematics and Physics (ZAMP), vol. 37, pp. 332-339, 1986.
• Richardson, J.F. and Zaki, W.N., Sedimentation and Fluidization: Part I, Transactions Institute of Chemical Engineers, 32, pp. 35, 1954.
• Savage, S. B. and Jeffrey, D. J., The Stress Tensor in a Granular Flow at High Shear rates, Journal of Fluid Mechanics, vol. 110, pp. 255-272, 1981.

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  14 July 2004
• Date of issue
  Sept 2004

History

• Accepted
  03 Oct 2003
• Received
  15 Apr 2003