How reliable is the mean-field nuclear matter description for supporting chiral effective Lagrangians?

How reliable is the mean-field nuclear matter description for supporting chiral effective Lagrangians?

A. Delfino¹, M. Malheiro ¹, and T. Frederico²

¹ Instituto de Física, Universidade Federal Fluminense,

24210-340, Niterói, R.J., Brazil

2Instituto Tecnológico da Aeronáutica

12331 São José dos Campos, São Paulo, Brazil

Received on 20 May, 2001

The link between non-linear chiral effective Lagrangians and the Walecka model description of bulk nuclear matter is questioned. This fact is by itself due to the Mean Field Approximation (MFA) which innuclear mater makes the picture of a nucleon-nucleon interaction based on scalar (vector) meson exchange equivalent to the description of a nuclear matter based on attractive and repulsive contact interactions. We present a linear chiral model where this link between the Walecka model and an underlying to chiral symmetry realization still holds, due to MFA.

Recently, a chiral effective Lagrangian description of nuclear matter has been suggested [1]. Such a proposal was based on adding a four-fermion Lagrangian term to a general Lagrangian proposed by Weinberg [2], describing the interactions of pions and nucleons in which the spontaneously broken SU(2) x SU(2) chiral symmetry is non-linearly realized. In short, the constructed non- linear chiral Lagrangian is

where

It turned out from that study that, at the mean-field level, the equations of state for this model are nothing but those obtained from the standard Walecka model [3] for infinite nuclear matter. Therefore, one gets the picture of a connection between a non-linear chiral Lagrangian and a baryonic phenomenological model. At the level of mean-field this is correct. In order to understand how far we can proceed beyond this picture it is important to see where all this comes from.

To study the properties of hadronic matter, Walecka [3] proposed a simple renormalizable model based on field theory, which is often referred to as Quantum Hadrodynamics (QHD). In this model nucleons interact through the exchange of s and w mesons, with s simulating medium range attraction and w simulating short-range repulsion. The usual approach to solve this model is the mean field approximation (MFA), in which the meson fields are replaced by their expectation values. A curious aspect of this model is that the scalar (vector) m_s (m_w) masses and g_s (g_w) coupling constants in the equations of state for infinite nuclear matter are eliminated in favour of C = gM²/m and C = gM²/m [4]. Since C and C are fitted to reproduce the nuclear matter bulk properties, values of m_s and m_w become irrelevant. It means that this model cannot distinguish between arbitrary values for the mesonic masses. Such arbitrariness can be extended to include infinite mesonic masses. If this is the case , one is led to the situation where the interaction between the nucleons is zero-range. By using attractive and repulsive contact interactions it is easy to show that the above conjecture is correct and therefore, a Zero Range Model (ZRM) is equivalent to the Walecka model for infinite nuclear matter at the MFA level. It means that, if we start with

where y's are baryonic fields, we arrive at the same equations of state of the Walecka model if one just multiplies by

M

² the coupling constants. This strange picture is therefore constructed from MFA itself applied for infinite nuclear matter, and has nothing strictly to do with chiral invariance. The Lagrangian given by Eq.(1) and the Lagrangian given by Eq.(3) lead to the same equations of state obtained from the Walecka Lagrangian at MFA level for infinite nuclear matter. They do not differ at the MFA level when surfaces effects are not included. Further distorted pictures could be obtained also for the self-coupling nonlinear s - w model [5, 6], if one adds terms such as

a(

)

³ and

b(

)

⁴ to the above Lagrangian which in this model become pure three- nucleon-and four-nucleon-forces respectively. A modification of the Walecka model, including higher orders of many-body forces, as suggested by Zimanyi and Moszkowski [7-9] also becomes equivalent to ZRM for infinite nuclear matter in MFA if one replaces

G

in Eq. (3) by

G

/ ( 1+ (

)/

M ).

To illustrate still further the risks of associating chiral symmetry to the Walecka model we show below that within MFA one cannot even distinguish if this symmetry is realized in a non-linear [1] or linear form. We start with the well-known Nambu-Jona-Lasinio(NJL) model [10], which has a linear realization of chiral symmetry. We include a vector interaction in a current-current form and the Lagrangian remains invariant under a linear chiral transformation of the baryon field y

For static, infinite nuclear matter, the three-vector momentum and spin dependent interaction average to zero due to rotational symmetry and the Lagrangian reduces to [11]

which is identical to that of Eq. (3) , except for the baryonic mass term. In the MFA, we linearize the interaction in Eq. (3) by closing the Fermi loop [12]. It means replacing (

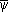
G

_ay)

² by 2

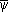
G

_ayá

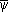
G

_ayñ. In nuclear matter we have only G

_a = 1 and g

_o. Here á

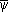
G

_ayñ is the vacuum (ground state) expectation value of the operators. For a Lorentz-invariant and parity-conserving vacuum, the only non-vanishing term is á

ñ.

So, in the same spirit of the dynamical quark mass generation mechanism of the NJL model [13], we can associate the nucleon rest mass M to

therefore obtaining a mean field Lagrangian identical to the ZRM model in MFA

where now á

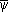
G

_ayñ means the expectation value of these operators in the nuclear matter ground state (all the nucleon states filled up to Fermi momentum) and g stands for the degeneracy factor equal to four. By looking at the problem in this perspective we have introduced a constraint, as in the standard NJL model. Thus, in order to have a non trivial nucleon mass solution for the Eq. (6), the coupling constant

G

must be greater than a critical value

G

_crit = (4p

²)/(g L

²). Here L is the cut-off which fixes the bare nucleon mass M given by the gap equation

where we have identified

G

to the Walecka coupling constant

C

/

M

² and

x =

k/

M is a dimensionless variable. By fixing M=938.27 MeV and the value of

C

which gives the correct nuclear matter saturation properties [14, 15] we have obtained L = 328.5MeV. Then, Eq.(7) will give also the same equation of state of the Walecka model, but now the chiral symmetry is 'realized' in a linear way. We are aware that our drawback to this chiral approach is the existence of a zero-frequency mode, the Nambu-Goldstone boson, which in this case is a pseudoscalar-isovector nucleon-antinucleon mode that we cannot identify to the pion.

In summary, all the arguments we have presented stress the difficulties of extracting , from a nuclear matter description at the MFA level, a justification of Walecka model coming from recent chiral effective Lagrangians [16]. To be more specific, if one adds to the Weinberg Lagrangian [2] the four-nucleon term, at the MFA level one arrives at a equivalent Walecka model as presented in ref. [1]. However, if we add any other term involving field derivatives which explicitly breaks the chiral symmetry we arrive also at an equivalent Walecka model. We have shown that the same procedure may be extended to a model where the chiral symmetry can be realized linearly. To conclude, we believe that what is in fact behind all of this is the fact that the MFA of Walecka model for infinite nuclear matter gives simply the same results of ZRM. We claim that is more appropriate and consistent to think just about a distorted picture furnished by MFA than to claim any chiral realization of hadronic phenomenological model. In this approximation, the pion which realizes the non-linear chiral symmetry cannot couple to the nucleons. So, the only way to conclude something about chiral effective Lagrangians describing bulk nuclear matter properties is to go beyond this approximation, where the identification with the Walecka model description will be lost.

This work has been partially supported by CNPq, Brazil.

References

[1] Graciela Gelmini, Bruce Ritzi, Phys.Lett. B357, 431 (1995).

[2] S. Weinberg, Phys.Rev.Lett.18, 188 (1967); Phys.Rev. 166, 1568 (1968); Physica A96, 372 (1979).

[3] J.D.Walecka, Ann. Phys. 83, 491 (1974); B.D. Serot and J.D. Walecka, Adv. in Nucl. Phys. vol.16, (Plenum, N.Y. 1986); B.D. Serot and J.D. Walecka, Int. J. Mod. Phys. E6, 515 (1997).

[4] A. Delfino, Lizardo H.C. Nunes and J.S. Sá Martins, Phys. Rev. CC57, 857 (1998); J.S. Sá Martins and A. Delfino, Phys. Rev. C61, 044615 (2000).

[5] A. Delfino, F.S. Navarra, M. Nielsen, R.B. Prandini and M. Chiapparini, Mod. Phys. Lett. A14, 1615 (1999).

[6] A.R. Taurines, C.A.Z. Vasconcellos, M. Malheiro and M. Chiapparini Phys. Rev. C63, 065801 (2001).

[7] J. Zimanyi and S.A. Moszkowski, Phys. Rev. C42, 1416 (1990).

[8] A. Delfino, C.T. Coelho and M. Malheiro, Phys. Rev. C51, 2188 (1995); M. Chiapparini, A. Delfino, M. Malheiro and A. Gattone Z. Phys. A357, 47 (1997).

[9] A.Delfino, M. Malheiro and D.P. Menezes Braz. J. of Phys. 27, 342 (1997).

[10] Y.Nambu and G. Jona-Lasinio, Phys. Rev.122, 245 (1961); 124, 246 (1961).

[11] U. Vogl and W. Weise, Prog. Part. and Nucl. Phys. 27, 95 (1991).

[12] S.P. Klevansky, Revs. of. Mod. Phys. 64, 649 (1992).

[13] E. M. Henley and G. Krein, Phys. Rev. Lett. 62, 2586 (1989).

[14] R.J. Furnsthal and B.D. Serot, Phys. Rev. C41, 1416 (1990).

[15] A. Delfino, C.T. Coelho, and M. Malheiro, Phys. Lett. B345, 361 (1995); M. Malheiro, A. Delfino and C.T. Coelho, Phys. Rev. C58, 426 (1998).

[16] R.J. Furnsthal, B.D. Serot and Hua-Bin Tang, Nucl. Phys. A615, 441 (1997).

Publication Dates

• Publication in this collection
  26 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  20 May 2001