Semiclassical Coulomb excitation matrix elements

Semiclassical Coulomb excitation matrix elements

B.V. Carlson^I; L.F. Canto^II; M.S. Hussein^III

^IDepartamento de Física, Instituto Tecnológico de Aeronáutica - CTA, 12228-900, São José dos Campos, SP, Brazil

^IIInstituto de Física da Universidade do Rio de Janeiro, CP 68528, 21945-970, Rio de Janeiro, RJ, Brazil

^IIIInstituto de Física, Universidade de São Paulo, CP 66318, 05389-970, São Paulo, SP, Brazil

ABSTRACT

Coulomb excitation matrix elements are often expressed in terms of the scalar electric potential and the electromagnetic fields. We show that, through an appropriate gauge transformation, the excitation matrix elements can always be expressed in terms of the electromagnetic fields alone. This change in representation becomes important when the widths of the excited states are taken into account.

1 Introduction

In an often cited work on Coulomb excitation[1] and in a more recent analysis of the same topic[2], the Coulomb excitation matrix elements are expressed in terms of the scalar electric potential and the electromagnetic fields. This representation of the interaction is adequate for use in a perturbative treatment and also provides a reasonably good estimate of the excitation cross section for states of zero width. In fact, in these two cases, the results are almost identical to those obtained by directly using the electromagnetic fields, or their derivatives, as these would appear in a classical treatment of the problem.

However, the mixed potential/field representation of the interaction is not adequate for a nonperturbative treatment of of excited states of finite width. In this case, the mixed representation yields large, unphysical cross sections due to the absorption of flux after excitation by the long-range potential term. The excitation cross section of a dipole transition, in particular, diverges in this case. This makes a treatment of multiple Coulomb excitation incorporating fluctuations contributions, such as those of the Brink-Axel type[3, 4, 5, 6,7], impossible in the mixed representation, since finite widths are a fundamental component of such models.

In the following, we show that, through an appropriate gauge transformation, the Coulomb excitation matrix elements can always be expressed in terms of the electromagnetic fields alone. Aside from making a satisfying parallel with the classical case, the pure field representation of the interaction matrix elements is found to provide physically reasonable cross sections[7].

2 Expanding the interaction Hamiltonian

The electromagnetic interaction Hamiltonian is given by

where j (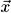, t) and 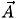(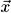, t) are the scalar and vector electromagnetic potentials, for which

and

and we assume r (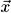, t) and (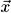, t) to be the charge and current density of a nucleus. We assume that the source of the electromagnetic field does not overlap the nucleus.

We want to obtain the first few terms contributing to the energy in the expansion of the electromagnetic fields about the center of the nucleus, 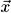= 0 . Such an expansion is reasonable if the electromagnetic fields are slowly varying over the extent of the nucleus[8] We thus take

and

where the subscript 0 on the fields and their derivatives denotes the evaluation of these at the point 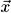= 0 .

Evaluation of the scalar potential terms is straightforward. Evaluation of the vector potential terms requires a bit more work. We use the continuity equation,

to derive two supplementary identities:

where the integral of the exact divergence is zero due to the finite extent of , and

which we rewrite as

Using the first of these, we can write

Using the second, we find

where the operator Ñ acts only the vector potential

₀ in the last term. We can manipulate the integrand of the second term further,

so that we may finally write for the entire term,

Putting all the pieces together, we have

We can write the second line in this expansion as

3 The Gauge Transformation

Let us define a gauge transformation L(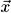, t) as

This gauge transformation will annul the integral above, since for

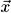^'(, t) = 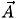(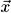, t)+ÑL(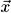, t),

It will not modify the magnetic field, since Ñ × ÑL(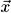, t) = 0. It will modify the scalar potential, however, which now becomes

Expanding the transformed scalar potential about 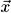= 0 , we find

so that, after the gauge transformation, we have for the interaction,

which we can rewrite in terms of the fields

₀ and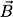 ₀ as

We can rewrite

since Ñ ·

₀ = 0 , because of our assumption that the field-producing charge does not overlap with the nuclear one. We can then write

where q is the charge,

is the eletric dipole operator,

the Q_ij are the traceless electric quadrupole operators,

and is the magnetic dipole operator,

4 Conclusions

As an example, we take as the potentials those due to a relativistic nucleus of charge Z passing on a straight-line trajectory with velocity v in the direction at a distance b₀ from the center of the charge/current distribution of interest. We then have

and

The electric field that results is

and

which, together with the matrix elements of the dipole operator , are all we need to describe excitations of the giant dipole resonance. Matrix elements for other multipolarities can be calculated similarly.

Bayman and Zardi[9] have noted that the mixed potential representation of the interaction matrix elements of Refs. [1] and [2] also neglects relativistic contributions to the quadrupole and higher multipolarity matrix elements that could become important at high energies. These are also taken into account correctly (and automatically) when the pure field representation is used.

BVC and MSH acknowledge support from FAPESP. The authors acknowledge partial support from the CNPq.

Received on 3 October, 2003

• [1] C.A. Bertulani, L.F. Canto, M.S. Hussein, and A.F.R. de Toledo Piza, Phys. Rev. C53, 334 (1996).
• [2] H. Esbensen and C.A. Bertulani, Phys. Rev. C65, 24605 (2002).
• [3] B.V. Carlson, M.S. Hussein, A.F.R. de Toledo Piza, and L.F. Canto, Phys. Rev. C60, 14604 (1999).
• [4] B.V. Carlson and M.S. Hussein, Phys. Rev. C59, R2343 (1999).
• [5] B.V. Carlson, L.F. Canto, S. Cruz-Barrios, M.S. Hussein, and A.F.R. de Toledo Piza, Ann. Phys. (New York) 276 111 (1999).
• [6] L.F. Canto, B.V. Carlson, M.S. Hussein, and A.F.R. de Toledo Piza, Phys. Rev. C60, 64624 (1999).
• [7] M.S. Hussein, B.V. Carlson, L.F. Canto, and A.F.R. de Toledo Piza, Phys. Rev. C66 34615 (2002).
• [8] J.D. Jackson, Classical Electrodynamics, J. Wiley and Sons, Inc., New York, 1962).
• [9] B.F. Bayman and Z. Zardi, Los Alamos Preprint Archives, nucl-th/0210060 (2001).

Publication Dates

• Publication in this collection
  26 Oct 2004
• Date of issue
  Sept 2004

History

• Received
  03 Oct 2003