Abstract
The Ogg-McCombe effective Hamiltonian for the electron in the conduction band together with the non-parabolic and effective-mass approximations were used in a theoretical study of the cyclotron effective mass and electron effective Landé g||-factor in semiconductor GaAs-Ga1-xAl xAs quantum wells under an applied magnetic field parallel to the growth direction of the quantum well. Calculations are performed as a function of the applied magnetic field, and for different widths of the GaAs-Ga1-xAl xAs quantum wells. Results for the electron cyclotron effective mass and g||-factor are found in quite good agreement with experimental data.
g-factor; Cyclotron effective mass; Quantum wells; Magnetic field
ELECTRONIC AND MAGNETIC PROPERTIES OF NANOSCOPIC SYSTEMS
Electron g-factor and cyclotron effective mass in semiconductor quantum wells under growth-direction applied magnetic fields
M. de Dios-LeyvaI; N. Porras-MontenegroII; H. S. BrandiIII, IV; L. E. OliveiraV
IDept. of Theor. Physics, Univ. of Havana, San Lázaro y L, Vedado 10400, Havana, Cuba
IIDepartamento de Física, Universidad del Valle, AA 25360, Cali - Colombia
IIIInstituto de Física, Univ. Federal do Rio de Janeiro, Rio de Janeiro - RJ, 21945-970, Brazil
IVInmetro, Campus de Xerém, Duque de Caxias - RJ, 25250-020, Brazil
VInstituto de Física, Unicamp, CP 6165, Campinas - SP, 13083-970, Brazil
ABSTRACT
The Ogg-McCombe effective Hamiltonian for the electron in the conduction band together with the non-parabolic and effective-mass approximations were used in a theoretical study of the cyclotron effective mass and electron effective Landé g||-factor in semiconductor GaAs-Ga1-xAlxAs quantum wells under an applied magnetic field parallel to the growth direction of the quantum well. Calculations are performed as a function of the applied magnetic field, and for different widths of the GaAs-Ga1-xAlxAs quantum wells. Results for the electron cyclotron effective mass and g||-factor are found in quite good agreement with experimental data.
Keywords: g-factor; Cyclotron effective mass; Quantum wells; Magnetic field
The understanding of the physics of semiconductor single and multiple quantum wells (QWs), quantum-well wires (QWWs), quantum dots (QDs), and superlattices (SLs) has been of great interest, and several studies have been performed to elucidate the physical properties of these systems [1-6]. The possible use of electron spins in the architecture of a solid-state based quantum computer has raised special attention in the study of the behavior of the electron spin coupled with an external magnetic field. In the single qubit operation it is of fundamental importance to have pure spin states in order to guarantee that no losses occur when the spins transport information [1]. This goal may be achieved by manipulating the electron g-factor in semiconductor heterostrucures and designing appropriate external gate control devices. The cyclotron effective mass and electronic g-factor are of importance in possible applications and in the interpretation of experimental data in specific research fields such as magneto-optical and magneto-transport studies, optically detected nuclear-resonance experiments, spin electronics and quantum beats measurements, and in the fractional and integer quantum Hall effects [2-6].
The appropriate calculation of the electron g-factor and cyclotron effective mass depends on the detailed understanding of the interaction between the externally applied magnetic field and electronic states of the semiconductor heterostructure. Techniques such as electron spin resonance, Hanle effect, spin quantum beats, spin flip Raman scattering experiments, and capacitance and energy spectroscopies [4-10] have been used to measure the electron g-factor in semiconductor systems. Lattice effects on the orbital contribution, quantum-confinement, and application of hydrostatic-pressure and external electric/magnetic fields may considerably modify the conduction-electron g-factor, in both magnitude and sign, in different semiconductor heterostructures. On the other hand, experimental measurements of both the Landé g-factor and cyclotron effective mass provide an excellent tool for testing theoretical predictions of band-structure electronic calculations in low-dimensional semiconductor heterostructures. In that respect, in this study we present a theoretical model which is used to give a proper physical and quantitative explanation of a series of experiments involving quantum beats and optically detected cyclotron resonance (ODCR) techniques applied in the measurements of g-factors and cyclotron effective masses of semiconductor GaAs-Ga1-xAlxAs QWs under growth-direction applied magnetic fields [2-5].
The Ogg-McCombe Hamiltonian, acting in the two-fold G6c spin-degenerate conduction band of the bulk materials of the GaAs-Ga1-xAlxAs QW under an applied magnetic field parallel to the growth z-direction, is obtained within the effective-mass approximation and in fourth-order of k.p perturbation theory as [11-18]
where  is the 2 x 2 unit matrix,
is the 2 x 2 unit matrix,  =
=  + e
+ e /
/ c,
c,  = -i Ñ, and the Landau gauge is used for the vector potential A = - y B
= -i Ñ, and the Landau gauge is used for the vector potential A = - y B . The ai, i = 1-6, are appropriate constants taken from Golubev et al [14] and with equal values for the well and barrier materials. V(z) is the square-well confining barrier potential, taken as 60% of the Ga1-xAlxAs and GaAs band-gap offset [19], and m* and g are the z growth-direction position-dependent conduction-electron effective mass and Landé g-factor, respectively [20]. The constant G is associated with the cubic Dresselhaus [21] spin-orbit term (due to the fact that GaAs has no inversion symmetry), lB =
. The ai, i = 1-6, are appropriate constants taken from Golubev et al [14] and with equal values for the well and barrier materials. V(z) is the square-well confining barrier potential, taken as 60% of the Ga1-xAlxAs and GaAs band-gap offset [19], and m* and g are the z growth-direction position-dependent conduction-electron effective mass and Landé g-factor, respectively [20]. The constant G is associated with the cubic Dresselhaus [21] spin-orbit term (due to the fact that GaAs has no inversion symmetry), lB =  is the Landau length, µB is the Bohr magneton,
is the Landau length, µB is the Bohr magneton,  = (
= ( x,
x, y,
y,  z), where the
z), where the  i are the Pauli matrices, and
i are the Pauli matrices, and  is a vector operator with components given as
is a vector operator with components given as  x =
x =  y
y
 zxz and corresponding cyclic permutations. The above Hamiltonian is a 2 x 2 conduction-band effective Hamiltonian [13-15], and includes effects of non-parabolicity by taking into account the coupling between the lowest G6c conduction band, G7v and G8v valence bands, and the G7c and G8c p-antibonding conduction bands. This Hamiltonian is expected to give a realistic description of the conduction-band Landau levels in zincblende-type semiconductors, semiconductor QWs, heterostructures, and so on. The second term in the RHS of (1) is the Zeeman contribution, the second-order in K spin-dependent terms (with the factors a4, a5, and a6) together with the third one (the spin-orbit Dresselhaus interaction), of third order in K, contribute to changes in the heterostructure effective g-factor. The terms in a1 and a3 govern the energy dependence of the cyclotron effective mass, whereas the term with the factor a2 gives the diamagnetic shift of the Landau electronic levels.
zxz and corresponding cyclic permutations. The above Hamiltonian is a 2 x 2 conduction-band effective Hamiltonian [13-15], and includes effects of non-parabolicity by taking into account the coupling between the lowest G6c conduction band, G7v and G8v valence bands, and the G7c and G8c p-antibonding conduction bands. This Hamiltonian is expected to give a realistic description of the conduction-band Landau levels in zincblende-type semiconductors, semiconductor QWs, heterostructures, and so on. The second term in the RHS of (1) is the Zeeman contribution, the second-order in K spin-dependent terms (with the factors a4, a5, and a6) together with the third one (the spin-orbit Dresselhaus interaction), of third order in K, contribute to changes in the heterostructure effective g-factor. The terms in a1 and a3 govern the energy dependence of the cyclotron effective mass, whereas the term with the factor a2 gives the diamagnetic shift of the Landau electronic levels.
Note that kx is a good quantum number (as  does not explicitly depend on x) and the eigenfunctions of
does not explicitly depend on x) and the eigenfunctions of  may be chosen as y(r) = j(y,z)
may be chosen as y(r) = j(y,z) , where Lx is the QW length along the x direction and y(r) and j(y,z) are two-component wavefunctions. We now write the Hamiltonian as
, where Lx is the QW length along the x direction and y(r) and j(y,z) are two-component wavefunctions. We now write the Hamiltonian as  = [
= [ 0 +
0 +  , where
, where  may be neglected, as it may be shown to contribute only small corrections to the energy levels [22] (details of the calculation will be published elsewhere [23]). The eigenfunctions of
may be neglected, as it may be shown to contribute only small corrections to the energy levels [22] (details of the calculation will be published elsewhere [23]). The eigenfunctions of  (or
(or  0) may then be written as
0) may then be written as


where the ± symbols correspond to  spin up or
spin up or  spin down states, respectively, with the eigenfunctions Fn(y) of the one-dimensional (1D) harmonic oscillator [24] given by
spin down states, respectively, with the eigenfunctions Fn(y) of the one-dimensional (1D) harmonic oscillator [24] given by
where the Hn are the Hermite polynomials, y0 = is the orbit-center position, and En =
is the orbit-center position, and En =  wc (n +
wc (n + ), with n = 0,1,2,..., and wc =
), with n = 0,1,2,..., and wc =  , are the corresponding 1D energies. Notice that the subindex m = 1,2,3,..., in both
, are the corresponding 1D energies. Notice that the subindex m = 1,2,3,..., in both  (z) and the associated electronic levels
(z) and the associated electronic levels  , indicates the m-th QW confined energy state, and n = 0,1,2,..., for a given m, represents the corresponding Landau subband energy levels [25]. The functions
, indicates the m-th QW confined energy state, and n = 0,1,2,..., for a given m, represents the corresponding Landau subband energy levels [25]. The functions  (z) and
(z) and  Landau energy levels may be obtained in a straightforward way [23] for a semiconductor GaAs-Ga1-xAlxAs QW. Of course, in the absence of the applied magnetic field, there are no Landau levels, the subband electronic states are only labelled by m, the problem reduces to that of confined electrons in a QW, and
Landau energy levels may be obtained in a straightforward way [23] for a semiconductor GaAs-Ga1-xAlxAs QW. Of course, in the absence of the applied magnetic field, there are no Landau levels, the subband electronic states are only labelled by m, the problem reduces to that of confined electrons in a QW, and  =
=  , with m being the subband index of the energy levels in a GaAs-Ga1-xAlxAs QW.
, with m being the subband index of the energy levels in a GaAs-Ga1-xAlxAs QW.
In order to compare our theoretical results with available experimental measurements, we present calculations performed for GaAs-Ga0.65Al0.35As QWs. Figure 1 displays the magnetic-field dependence of the  electronic Landau levels, the cyclotron effective mass
electronic Landau levels, the cyclotron effective mass
the two-dimensional (2D) cyclotron effective mass
and parallel g factor,
for an L = 50 Å GaAs-Ga0.65Al0.35As QW. The definition of the  cyclotron effective mass is convenient for comparison with experimental measurements involving transitions between consecutive Landau levels, whereas the
cyclotron effective mass is convenient for comparison with experimental measurements involving transitions between consecutive Landau levels, whereas the  2D cyclotron effective mass is appropriate for experiments associated with, for instance, resonant magnetotunneling in double barrier heterostructures [26]. Results shown in Figure 1 correspond to calculations associated to the electronic levels of the first m = 1 subband of Landau states. The nonlinear behavior of the
2D cyclotron effective mass is appropriate for experiments associated with, for instance, resonant magnetotunneling in double barrier heterostructures [26]. Results shown in Figure 1 correspond to calculations associated to the electronic levels of the first m = 1 subband of Landau states. The nonlinear behavior of the  Landau electronic levels in Fig. 1(a) is due to the presence of non-parabolic terms in the Hamiltonian, and it is apparent that the effects of nonlinearity are stronger for the highest Landau levels and large values of the applied magnetic field, as compared with the effects on the lowest Landau states. The above mentioned properties of the Landau energy levels lead to the behavior of the cyclotron masses as shown in Figs. 1(b) and 1(c), which evolve from an essentially linear function of the applied magnetic field, for the lowest levels and small values of B, to a strong nonlinear behavior as a function of B, for the highest Landau levels and large values of the applied field. The field-dependence of the g||-factor [cf. Fig. 1(d)] is due both to the magnetic-field effect on the electronic Landau levels as well as to the confinement/barrier penetration of the electron envelope wave function due to the presence of the Ga0.65Al0.35As barriers. Although not shown here, for large values of the QW width, e.g., L
Landau electronic levels in Fig. 1(a) is due to the presence of non-parabolic terms in the Hamiltonian, and it is apparent that the effects of nonlinearity are stronger for the highest Landau levels and large values of the applied magnetic field, as compared with the effects on the lowest Landau states. The above mentioned properties of the Landau energy levels lead to the behavior of the cyclotron masses as shown in Figs. 1(b) and 1(c), which evolve from an essentially linear function of the applied magnetic field, for the lowest levels and small values of B, to a strong nonlinear behavior as a function of B, for the highest Landau levels and large values of the applied field. The field-dependence of the g||-factor [cf. Fig. 1(d)] is due both to the magnetic-field effect on the electronic Landau levels as well as to the confinement/barrier penetration of the electron envelope wave function due to the presence of the Ga0.65Al0.35As barriers. Although not shown here, for large values of the QW width, e.g., L  200 Å, the influence of the barriers on the Landau levels is negligible as compared to that of the magnetic field, the electronic envelope wave functions essentially do not penetrate in the Ga0.65Al0.35As barriers, and the g|| field dependence, for n = 0, on the QW width is small. Calculated results for the mc cyclotron effective mass as a function of the width of the GaAs-Ga0.65Al0.35As QW are depicted in Fig. 2 and compared with experimental results by Singleton et al [2] and Michels et al [3]. Theoretical results are for small values of the applied magnetic field (B
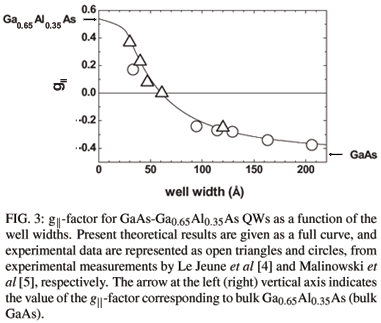
200 Å, the influence of the barriers on the Landau levels is negligible as compared to that of the magnetic field, the electronic envelope wave functions essentially do not penetrate in the Ga0.65Al0.35As barriers, and the g|| field dependence, for n = 0, on the QW width is small. Calculated results for the mc cyclotron effective mass as a function of the width of the GaAs-Ga0.65Al0.35As QW are depicted in Fig. 2 and compared with experimental results by Singleton et al [2] and Michels et al [3]. Theoretical results are for small values of the applied magnetic field (B  0), and for the m = 1, n = 0 Landau level. As one may see from Fig. 2, the agreement with experimental data by Michels et al [3] is excellent, and we find a fair only agreement with the open triangle value by Singleton et al [2]. Figure 3 shows the present theoretical results for the g||-factor, in the case of the m = 1, n = 0 Landau level, as a function of the GaAs-Ga0.65Al0.35As QW width. Again, calculated results are for small values of the growth-direction applied magnetic field (B
0), and for the m = 1, n = 0 Landau level. As one may see from Fig. 2, the agreement with experimental data by Michels et al [3] is excellent, and we find a fair only agreement with the open triangle value by Singleton et al [2]. Figure 3 shows the present theoretical results for the g||-factor, in the case of the m = 1, n = 0 Landau level, as a function of the GaAs-Ga0.65Al0.35As QW width. Again, calculated results are for small values of the growth-direction applied magnetic field (B  0 - 4 T), and are compared with the experimental data by Le Jeune et al [4] (for B in the range from 1 T to 4 T), and Malinowski et al [5] (for B = 4 T). Notice that, for large QW widths, the value of the g||-factor approaches the g = - 0.44 value of bulk GaAs, as expected. Also, it is apparent in Fig. 3 that the present theoretical calculations are in excellent agreement with the experimental measurements.
0 - 4 T), and are compared with the experimental data by Le Jeune et al [4] (for B in the range from 1 T to 4 T), and Malinowski et al [5] (for B = 4 T). Notice that, for large QW widths, the value of the g||-factor approaches the g = - 0.44 value of bulk GaAs, as expected. Also, it is apparent in Fig. 3 that the present theoretical calculations are in excellent agreement with the experimental measurements.
Summing up, we have used the effective-mass approximation and taken into account the non-parabolic-band effects via the Ogg-McCombe effective Hamiltonian, to theoretically evaluate the electronic Landau levels, cyclotron effective masses and g||-factors of GaAs-Ga1-xAlxAs semiconductor QWs. The characteristic problem of the Ogg-McCombe Hamiltonian is solved by expressing the corresponding spin  and
and  envelope wave functions as products of harmonic-oscillator and QW wave functions. We have obtained the
envelope wave functions as products of harmonic-oscillator and QW wave functions. We have obtained the  cyclotron effective mass, the
cyclotron effective mass, the  and the g||-factor as functions of the QW widths and growth-direction applied magnetic fields, with the calculated results exhibiting a noticeable dependence on the strength of the applied magnetic field. Finally, present theoretical calculations for the Landé cyclotron effective mass and g||-factor in isolated GaAs-(Ga,Al)As QWs were found in quite good agreement with the experimental measurements reported by Singleton et al [2], Michels et al [3], Le Jeune et al [4] and Malinowski et al [5].
and the g||-factor as functions of the QW widths and growth-direction applied magnetic fields, with the calculated results exhibiting a noticeable dependence on the strength of the applied magnetic field. Finally, present theoretical calculations for the Landé cyclotron effective mass and g||-factor in isolated GaAs-(Ga,Al)As QWs were found in quite good agreement with the experimental measurements reported by Singleton et al [2], Michels et al [3], Le Jeune et al [4] and Malinowski et al [5].
Acknowledgments
The authors would like to thank the Colombian COLCIENCIAS Agency (under Grant No. 1106-05-13828) and Brazilian Agencies CNPq, FAPESP, FAPERJ, FUJB, Rede Nacional de Materiais Nanoestruturados/CNPq, and MCT - Millenium Institute for Quantum Computing/MCT for partial financial support. MdDL and NPM wish to thank the warm hospitality of the Institute of Physics, State University of Campinas, Brazil, where part of this work was performed.
[1] I. Zutic, J. Fabian, and S. Das Sarma, Rev. Mod. Phys. 76, 323 (2004).
[2] J. Singleton, R. J. Nicholas, and D. C. Rogers, Surf. Sci. 196, 429 (1988).
[3] J. G. Michels, R. J. Warbuton, R. J. Nicholas, J. J. Harris, and C. T. Foxon, Physica B 184, 159 (1993).
[4] P. Le Jeune, D. Robart, X. Marie, T. Amand, M. Brosseau, J. Barrau, V. Kalevich, and D. Rodichev, Sem. Sci. Tech. 12, 380 (1997).
[5] A. Malinowski and R. T. Harley, Phys. Rev. B 62, 2051 (2000).
[6] Y. K. Kato, R. C. Myers, A. C. Gossard, and D. D. Awschalom, Science 306, 1910 (2004).
[7] M. Dobers, K. von Klitzing, and G. Weimann, Phys. Rev. B 38, 5453 (1988).
[8] V. F. Sapega, T. Ruf, M. Cardona, K. Ploog, E. L. Ivchenko, and D. N. Mirlin, Phys. Rev. B 50, 2510 (1994).
[9] G. Medeiros-Ribeiro, M. V. B. Pinheiro, V. L. Pimentel, and E. Marega, Appl. Phys. Lett. 80, 4229 (2002).
[10] A. S. Bracker, E. A. Stinaff, D. Gammon, M. E. Ware, J. G. Tischler, A. Shabaev, Al. L. Efros, D. Park, D. Gershoni, V. L. Korenev, and I. A. Merkulov, Phys. Rev. Lett. 94, 047402 (2005).
[11] N. R. Ogg, Proc. Phys. Soc. 89, 431 (1966).
[12] B. O. McCombe, Phys. Rev. 181, 1206 (1969).
[13] M. Braun and U. Rossler, J. Phys. C 18, 3365 (1985).
[14] V. G. Golubev, V. I. Ivanov-Omskii, I. G. Minervin, A. V. Osutin, and D. G. Polyakov, Sov. Phys. JETP 61, 1214 (1985).
[15] G. Lommer, F. Malcher, and U. Rössler, Superlatt. and Microstruct. 2, 273 (1986).
[16] M. de Dios-Leyva, J. Lopez-Gondar, and J. Sabin del Valle, Phys. Stat. Sol. (b) 148, K113 (1988); J. Sabin del Valle, J. Lopez-Gondar, and M. de Dios-Leyva, Phys. Stat. Sol. (b) 151, 127 (1989).
[17] E. L. Ivchenko and A. A. Kiselev, Sov. Phys. Semicond. 26, 827 (1992).
[18] A. Bruno-Alfonso, L. Diago-Cisneros, and M. de Dios-Leyva, J. Appl. Phys. 77, 2837 (1995).
[19] E. H. Li, Physica E 5, 215 (2000).
[20] Here we use the following bulk values of GaAs: mc = 0.0665 m0 and g(GaAs) = - 0.44, and of Ga0.65Al0.35As: mc = 0.1034 m0 and g(Ga0.65Al0.35As) = + 0.54. The g-factor values are from Le Jeune et al [4] and the conduction-band masses were taken from Li [19].
[21] G. Dresselhaus, Phys. Rev. 100, 580 (1955).
[22] Here we refer to de Dios-Leyva et al [16] for the expressions of $\hat{H_0}$ and $\hat{W}$.
[23] M. de Dios-Leyva, N. Porras-Montenegro, H. S. Brandi, and L. E. Oliveira, J. Appl. Phys. (submitted for publication).
[24] It is straightforward to show that the operator $\hat{N}=\hat{a}^+ \hat{a}^- \frac{1}{2}$, with $\hat{a}^\pm = - \frac{1_B}{\sqrt{2}}, (\hat{K_x}\pm i \hat{K_y}$, commutes with $\hat{H}$ and, therefore, it is possible to find a complete set of common eigenfunctions of both $\hat{N}$ and $\hat{H}$.
[25] One should notice that the electronic Landau energies are independent of the y0 orbit-center position, due to the translational invariance of the Hamiltonian in the in-plane y direction.
[26] E. E. Mendez, L. Esaki, and W. I. Wang, Phys. Rev. B 33, 2893 (1986).
Received on 8 December, 2005
- [1] I. Zutic, J. Fabian, and S. Das Sarma, Rev. Mod. Phys. 76, 323 (2004).
- [2] J. Singleton, R. J. Nicholas, and D. C. Rogers, Surf. Sci. 196, 429 (1988).
- [3] J. G. Michels, R. J. Warbuton, R. J. Nicholas, J. J. Harris, and C. T. Foxon, Physica B 184, 159 (1993).
- [4] P. Le Jeune, D. Robart, X. Marie, T. Amand, M. Brosseau, J. Barrau, V. Kalevich, and D. Rodichev, Sem. Sci. Tech. 12, 380 (1997).
- [5] A. Malinowski and R. T. Harley, Phys. Rev. B 62, 2051 (2000).
- [6] Y. K. Kato, R. C. Myers, A. C. Gossard, and D. D. Awschalom, Science 306, 1910 (2004).
- [7] M. Dobers, K. von Klitzing, and G. Weimann, Phys. Rev. B 38, 5453 (1988).
- [8] V. F. Sapega, T. Ruf, M. Cardona, K. Ploog, E. L. Ivchenko, and D. N. Mirlin, Phys. Rev. B 50, 2510 (1994).
- [9] G. Medeiros-Ribeiro, M. V. B. Pinheiro, V. L. Pimentel, and E. Marega, Appl. Phys. Lett. 80, 4229 (2002).
- [10] A. S. Bracker, E. A. Stinaff, D. Gammon, M. E. Ware, J. G. Tischler, A. Shabaev, Al. L. Efros, D. Park, D. Gershoni, V. L. Korenev, and I. A. Merkulov, Phys. Rev. Lett. 94, 047402 (2005).
- [11] N. R. Ogg, Proc. Phys. Soc. 89, 431 (1966).
- [12] B. O. McCombe, Phys. Rev. 181, 1206 (1969).
- [13] M. Braun and U. Rossler, J. Phys. C 18, 3365 (1985).
- [14] V. G. Golubev, V. I. Ivanov-Omskii, I. G. Minervin, A. V. Osutin, and D. G. Polyakov, Sov. Phys. JETP 61, 1214 (1985).
- [15] G. Lommer, F. Malcher, and U. Rössler, Superlatt. and Microstruct. 2, 273 (1986).
- [16] M. de Dios-Leyva, J. Lopez-Gondar, and J. Sabin del Valle, Phys. Stat. Sol. (b) 148, K113 (1988);
- J. Sabin del Valle, J. Lopez-Gondar, and M. de Dios-Leyva, Phys. Stat. Sol. (b) 151, 127 (1989).
- [17] E. L. Ivchenko and A. A. Kiselev, Sov. Phys. Semicond. 26, 827 (1992).
- [18] A. Bruno-Alfonso, L. Diago-Cisneros, and M. de Dios-Leyva, J. Appl. Phys. 77, 2837 (1995).
- [19] E. H. Li, Physica E 5, 215 (2000).
- [21] G. Dresselhaus, Phys. Rev. 100, 580 (1955).
- [23] M. de Dios-Leyva, N. Porras-Montenegro, H. S. Brandi, and L. E. Oliveira, J. Appl. Phys. (submitted for publication).
- [26] E. E. Mendez, L. Esaki, and W. I. Wang, Phys. Rev. B 33, 2893 (1986).
Publication Dates
-
Publication in this collection
29 Nov 2006 -
Date of issue
Sept 2006
History
-
Received
08 Dec 2005