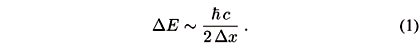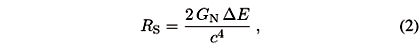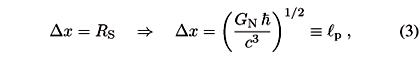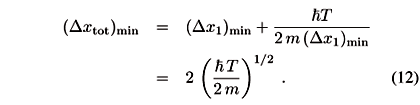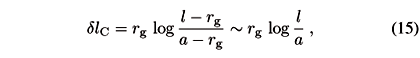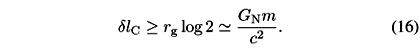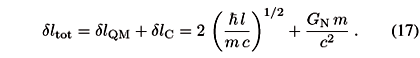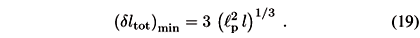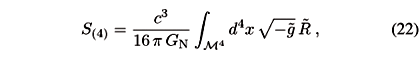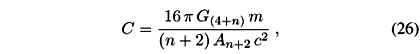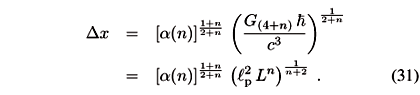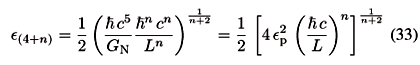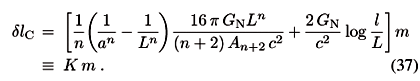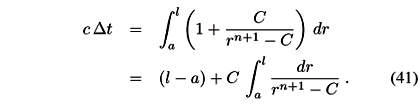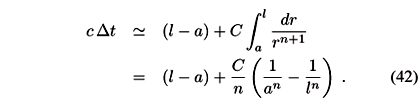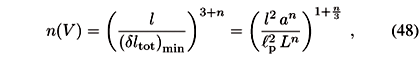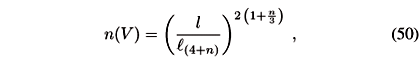Generalized uncertainty principle, extra-dimensions and holography

Generalized uncertainty principle, extra-dimensions and holography

Fabio Scardigli^I; Roberto Casadio^II

^ICENTRA - Departamento de Fisica, Instituto Superior Tecnico, Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal

^IIDipartimento di Fisica, Università di Bologna and I.N.F.N., Sezione di Bologna, via Irnerio 46, 40126 Bologna, Italy

ABSTRACT

We consider Uncertainty Principles which take into account the role of gravity and the possible existence of extra spatial dimensions. Explicit expressions for such Generalized Uncertainty Principles in 4+n dimensions are given and their holographic properties investigated. In particular, we show that the predicted number of degrees of freedom enclosed in a given spatial volume matches the holographic counting only for one of the available generalizations and without extra dimensions.

1 Introduction

During the last years many efforts have been devoted to clarifying the role played by the existence of extra spatial dimensions in the theory of gravity 1,2]. One of the most interesting predictions drawn from the theory is that there should be measurable deviations from the 1/r² law of Newtonian gravity at short (and perhaps also at large) distances. Such new laws of gravity would imply modifications of those Generalized Uncertainty Principles (GUP's) designed to account for gravitational effects in the measure of positions and energies.

On the other hand, the holographic principle is claimed to apply to all of the gravitational systems. The existence of GUP's satisfying the holography in four dimensions (one of the main examples is due to Ng and Van Dam [3]) led us to explore the holographic properties of the GUP's extended to the brane-world scenarios [4]. The results, at least for the examples we considered, are quite surprising. The expected holographic scaling indeed seems to hold only in four dimensions, and only for the Ng and van Dam's GUP. When extra spatial dimensions are admitted, the holography is destroyed. This fact allows two different interpretations: either the holographic principle is not universal and does not apply when extra dimensions are present; or, on the contrary, we take seriously the holographic claim in any number of dimensions, and our results are therefore evidence against the existence of extra dimensions.

The four-dimensional Newton constant is denoted by G_N throughout the paper.

2 Linear GUP in four dimensions from micro black holes

In this Section we derive a GUP via a micro black hole gedanken experiment, following closely the content of Ref. [5].

When we measure a position with precision of order Dx, we expect quantum fluctuations of the metric field around the measured position with energy amplitude

The Schwarzschild radius associated with the energy DE,

falls well inside the interval Dx for practical cases. However, if we wanted to improve the precision indefinitely, the fluctuation DE would grow up and the corresponding R_S would become larger and larger, until it reaches the same size as Dx. As it is well known, the critical length is the Planck length,

and the associated energy is the Planck energy

If we tried to further decrease Dx, we should concentrate in that region an energy greater than the Planck energy, and this would enlarge further the Schwarzschild radius R_S, hiding more and more details of the region beyond the event horizon of the micro hole. The situation can be summarized by the inequalities

which, if combined linearly, yield

This is a generalization of the uncertainty principle to cases in which gravity is important, i.e. to energies of the order of Î_p. We note that the minimum value of Dx is reached for (DE)_min = Î_p and is given by (Dx)_min = 2 l_p.

2.1 Holographic properties

In this section, we investigate the holographic properties of the GUP proposed above. We shall estimate the number of degrees of freedom n(V) contained in a spatial volume (cube or "hypercube'') of size l. The holographic principle claims that n(V) scales as the area of the (hyper-)surface enclosing the given volume, that is (l/l_p)²⁺ⁿ in 4+n dimensions.

For the four-dimensional GUP considered in the previous section, Eq. (6), we find that this scaling does not occur. In fact, (Dx)_min ~ l_p and a cube of side l contains a number of degrees of freedom equal to

We then conclude that this GUP, obtained by linearly combining the quantum mechanical expression with gravitational bounds, does not imply the holographic counting of degrees of freedom.

3 Ng and Van Dam GUP in four dimensions

An interesting GUP that satisfies the holographic principle in four dimensions has been proposed by Ng and van Dam [3], based on Wigner inequalities about distance measurements with clocks and light signals [6].

Suppose we wish to measure a distance l. Our measuring device is composed of a clock, a photon detector and a photon gun. A mirror is placed at the distance l which we want to measure and m is the mass of the system "clock + photon detector + photon gun''. We call "detector'' the whole system and let a be its size. Obviously, we suppose

which means that we are not using a black hole as a clock. Be Dx₁ the uncertainty in the position of the detector, then the uncertainty in the detector's velocity is

After the time T = 2 l/c taken by light to travel along the closed path detector-mirror-detector, the uncertainty in the detector's position (i.e. the uncertainty in the actual length of the segment l) has become

We can minimize Dx_tot by suitably choosing Dx₁,

Hence

Since T = 2 l/c, we have

This is a purely quantum mechanical result obtained for the first time by Wigner in 1957 [6]. From Eq. (13), it seems that we can reduce the error (Dx_tot)_min as much as we want by choosing m very large, since (Dx_tot)_min ® 0 for m ® ¥. But, obviously, here gravity enters the game.

In fact, Ng and van Dam have also considered a further source of error, a gravitational error, besides the quantum mechanical one already addressed. Suppose the clock has spherical symmetry, with a > r_g. Then the error due to curvature can be computed from the Schwarzschild metric surrounding the clock. The optical path from r₀ > r_g to a generic point r > r₀ is given by (see, for example, Ref. [7])

and differs from the "true'' (spatial) length (r – r₀). If we put a = r₀, l = r, the gravitational error on the measure of (l – a) is thus

where the last estimate holds for l > a >> r_g.

If we measure a distance l > 2a, then the error due to curvature is

Thus, according to Ng and van Dam the total error is

This error can be minimized again by choosing a suitable value for the mass of the clock,

and, inserting m_min in Eq. (17), we then have

The global uncertainty on l contains therefore a term proportional to l^1/3.

3.1 Holographic properties

We now see immediately the beauty of the Ng and van Dam GUP: it obeys the holographic scaling. In fact in a cube of size l the number of degrees of freedom is given by

as required by the holographic principle.

4 Models with n extra dimensions

We shall now generalize the procedure outlined in a previous section to a space-time with 4+n dimensions, where n is the number of space-like extra dimensions [4]. The first problem we should address is how to relate the gravitational constant G_N in four dimensions with the one in 4+n, henceforth denoted by G_(4+n).

This of course depends on the model of space-time with extra dimensions that we consider. Models recently appeared in the literature mostly belong to two scenarios:

• the Arkani-Hamed-Dimopoulos-Dvali (ADD) model [1], where the extra dimensions are compact and of size L;

• the Randall-Sundrum (RS) model [2], where the extra dimensions have an infinite extension but are warped by a non-vanishing cosmological constant.

A feature shared by (the original formulations of) both scenarios is that only gravity propagates along the n extra dimensions, while Standard Model fields are confined on a four-dimensional sub-manifold usually referred to as the brane-world .

In the ADD case the link between G_N and G_(4+n) can be fixed by comparing the gravitational action in four dimensions with the one in 4+n dimensions. The space-time topology in such models is , where is the usual four-dimensional space-time and Âⁿ represents the extra dimensions of finite size L. The space-time brane has no tension and therefore the action S_(4+n) can be written as

where , are the projections on of R and g. Here Lⁿ is the "volume'' of the extra dimensions and we omitted unimportant numerical factors. On comparing the above expression with the purely four-dimensional action

we obtain

The RS models are more complicated. It can be shown [2] that for n = 1 extra dimension we have G_(4+n) = s^–1G_N, where s is the brane tension with dimensions of length^–1 in suitable units. The gravitational force between two point-like masses m and M on the brane is now given by

where the correction to Newton law comes from summing over the extra dimensional graviton modes in the graviton propagator [2]. However, since Eq. (24) is obtained by perturbative calculations, not immediately applicable to a non-perturbative structure such as a black hole, we shall consider only the ADD scenario in this paper. To be more precise, from table-top tests of the gravitational force one finds that n > 2 in ADD [1,8]. On the other hand, black holes with mass M << s^–1 are likely to behave as pure five-dimensional in RS [9], therefore our results for n = 1 should apply to such a case.

5 Ng and Van Dam GUP in 4+n dimensions

Ng and van Dam's derivation can be generalized to the case with n extra dimensions. The Wigner relation (13) for the quantum mechanical error is not modified by the presence of extra dimensions and we just need to estimate the error dl_C due to curvature.

We ought not to consider micro black holes created by the fluctuations DE in energy, as in Section 2, but we have rather to deal with (more or less) macroscopic clocks and distances. This implies that we have to distinguish four different cases:

1. 0 < L < r_g < a < l;

2. 0 < r_(4+n) < L < a < l;

3. 0 < r_(4+n) < a < L < l;

4. 0 < r_(4+n) < a < l < L;

where r_(4+n) is the Schwarzschild radius of the detector in 4+n dimensions, and of course r_g = r₍₄₎. The curvature error will be estimated (as before) by computing the optical path from a º r₀ to l º r. Of course, we will use a metric which depends on the relative size of L with respect to a and l, that is the usual four-dimensional Schwarzschild metric in the region r > L, and the 4+n dimensional Schwarzschild solution in the region r < L (where the extra dimensions play an actual role).

In cases 1. and 2 the length of the optical path from a to l can be obtained using just the four-dimensional Schwarzschild solution and the result is given by Eq. (19).

In cases 3. and 4. we instead have to use the Schwarzschild solution in 4+n dimensions [11],

at least for part of the optical path. In the above,

and A_n+2 is the area of the unit (n+2)-sphere, that is

Besides, we note that, for n = 0,

that is, C coincides in four dimensions with the Schwarzschild radius of the detector. The Schwarzschild horizon is located where (1 – C/rⁿ⁺¹) = 0, that is at r = C^1/(n+1)º r_(4+n), or

where

is an unimportant numerical factor.

Since measurements can be performed only on the brane, to the uncertainty Dx in position we can still associate an energy given by Eq (1). The corresponding Schwarzschild radius is now given by Eq. (29) with m = DE/c² and the critical length such that Dx = r_(4+n) is the Planck length in 4+n dimensions,

For sake of simplicity (because a(0) = 1 and in any case a(n) ~ 1) we define the Planck length in 4+n dimensions as

The energy associated with l_(4+n) is analogously the Planck energy in 4+n dimensions,

where Î_p is the Planck energy in four dimensions given in Eq. (4).

In case 3. we obtain the length of the optical path from a to l by adding the optical path from a to L and that from L to l. We must use the solution in 4+n dimensions for the first part, and the four-dimensional solution for the second part of the path,

It is not difficult to show that from r_(4+n) < L (which holds in cases 3. and 4.) we can infer

Now, suppose aⁿ⁺¹ >> C = , that is a >> r_(4+n), so that we are not doing measures inside a black hole. Then r_g < r_(4+n) << a < L < l and

The error caused by the curvature (when a < L < l) is therefore linear in m,

We recall that the curvature error in four dimensions does not contain the size of the clock. On the contrary, this error in 4+n dimensions depends explicitly on the size a of the clock and on the size L of the extra dimensions. Hence the total error is given by

where J = 2 (l/c)^1/2 and K is defined above. This error can be minimized with respect to m,

Finally,

where we used the definition of J and K.

In case 4., the optical path from a to l can be obtained by using simply the Schwarzschild solution in 4+n dimensions. We get

Suppose now, as before, that aⁿ⁺¹ >> C = , that is a >> r_(4+n) (i.e. our clock is not a black hole). We then have

If the distance we are measuring is, at least, of the size of the clock (l > 2 a), we can write

The error caused by the curvature is therefore (when a < l < L)

Here we again note that the curvature error in 4+n dimensions explicitly contains the size of the clock. The global error can be computed as before

where C is linear in m. Minimizing dl_tot with respect to m can be done in perfect analogy with the previous calculation. The result is

We note that the expression (40) coincides in the limit L ® a with Eq. (19) (taking l > 2 a), while, in the limit L ® l, we recover from Eq. (40) the expression (46) (of course, supposing also that l > 2 a).

5.1 Holographic properties

We finally examine the holographic properties of Eq. (46) for the GUP of Ng and van Dam type in 4+n dimensions. We just consider the expression in Eq. (46) because it also represents the limit of Eq. (40) for L ® l and l > 2 a. Moreover, for n = 0, Eq. (46) yields the four-dimensional error given in Eq. (19).

Since we are just interested in the dependence of n(V) on l and the basic constants, we can write

We then have that the number of degrees of freedom in the volume of size l is

and the holographic counting holds in four-dimensions (n = 0) but is lost when n > 0. In fact we do not get something as

as we would expect in 4+n dimensions. Even if we take the ideal case a ~ l_(4+n) we get

and the holographic principle does not hold for n > 0.

6 Concluding remarks

In the previous Sections, we have shown that the holographic principle seems to be satisfied only by uncertainty relations in the version of Ng and van Dam and for n = 0. That is, only in four dimensions we are able to formulate uncertainty principles which predict the same number of degrees of freedom per spatial volume as the holographic counting. This could be evidence for questioning the existence of extra dimensions. Moreover, such an argument based on holography could also be used to support the compactification of string theory down to four dimensions, given that there seems to be no firm argument which forces the low energy limit of string theory to be four-dimensional (except for the obvious observation of our world). In this respect, we should also say that the cases 3. and 4 of Section 5 do not have a good probability to be realized in nature since, if there are extra spatial dimensions, their size must be shorter than 10^–1 mm [8]. Therefore, cases 1. and 2. of Section 5 are more likely to survive the test of future experiments.

A number of general remarks are however in order. First of all, we cannot claim that our list of possible GUP's is complete and other relations might be derived in different contexts which accommodate for both the holography and extra dimensions. Further, one might find hard to accept that quantum mechanics and general relativity enter the construction of GUP's on the same footing, since the former is supposed to be a fundamental framework for all theories while the latter can be just regarded as a (effective) theory of the gravitational interaction. We might agree on the point of view that GUP's must be considered as "effective'' (phenomenological) bounds valid at low energy (below the Planck scale) rather than "fundamental'' relations. This would in fact reconcile our result that four dimensions are preferred with the fact that string theory (as a consistent theory of quantum gravity) requires more dimensions through the compactification which must occur at low energy, as we mentioned above. Let us also note that general relativity (contrary to usual field theories) determines the space-time including the causality structure, and the latter is an essential ingredient in all actual measurements. It is therefore (at least) equally hard to conceive uncertainty relations which neglect general relativity at all. This conclusion would become even stronger in the presence of extra dimensions, since the fundamental energy scale of gravity is then lowered [1,2] (possibly) within the scope of present or near-future experiments and the gravitational radius of matter sources is correspondingly enlarged [10].

A final remark regards cases with less than four dimensions. Since Einstein gravity does not propagate in such space-times and no direct analogue of the Schwarzschild solution exists, one expects a qualitative difference with respect to the cases that we have considered here. For instance, a point-like source in three dimensions would generate a flat space-time with a conical singularity and no horizon [12]. Consequently, one does expect that the usual Heisenberg uncertainty relations hold with no corrections for gravity.

References

[1] N. Arkani-Hamed, S. Dimopoulos and G. Dvali, Phys. Lett. B 429, 263 (1998); Phys. Rev. D 59, 0806004 (1999); I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos and G. Dvali, Phys. Lett. B 436, 257 (1998).

[2] L. Randall and R. Sundrum, Phys. Rev. Lett. 83, 3370 (1999); Phys. Rev. Lett. 83, 4690 (1999).

[3] Y.J. Ng and H. van Dam, Mod. Phys. Lett. A 9, 335 (1994); Mod. Phys. Lett. A 10, 2801 (1995); Phys. Lett. B 477, 429 (2000); Y.J. Ng, Phys. Rev. Lett. 86, 2946 (2001).

[4] F. Scardigli and R. Casadio, Class. Qu. Grav. 20, 3915 (2003).

[5] F. Scardigli, Phys. Lett. B 452, 39 (1999).

[6] E.P. Wigner, Rev. Mod. Phys. 29, 255 (1957); H. Salecker and E.P. Wigner, Phys. Rev. 109, 571 (1958).

[7] L.D. Landau and E.M. Lifshitz, The classical theory of fields (Pergamon Press, Oxford, 1975).

[8] C.D. Hoyle et al., Phys. Rev. Lett. 86, 1418 (2001).

[9] S.B. Giddings, E. Katz, and L. Randall, JHEP 0003, 023 (2000); J. Garriga and T. Tanaka, Phys. Rev. Lett. 84, 2778 (2000).

[10] P.C. Argyres, S. Dimopoulos, and J. March-Russell, Phys. Lett. B 441, 96 (1998).

[11] R.C. Myers and M.J. Perry, Ann. Phys. 172, 304 (1986).

[12] In three dimensions with negative cosmological constant one also has the BTZ black hole which forms when two point-like particles collide provided certain initial conditions are satisfied. For a recent review, see Ref. [13].

[13] D. Birmingham, I. Sachs, and S. Sen, Int. J. Mod. Phys. D 10, 833 (2001).

Received on 23 December, 2004

Publication Dates

• Publication in this collection
  06 Sept 2005
• Date of issue
  June 2005

History

• Received
  23 Dec 2004