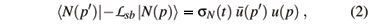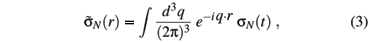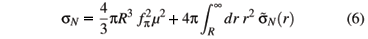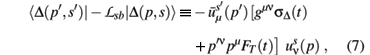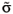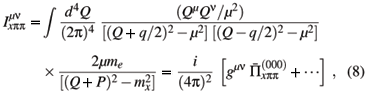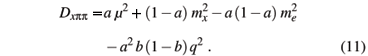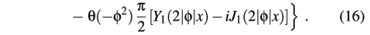Nucleon and delta sigma-terms

Abstract

We evaluate nucleon and delta sigma-terms and obtain the results 43 MeV < sigmaN < 49 MeV and 28 MeV < <FONT FACE=Symbol>sD</FONT> < 32 MeV, depending on the coupling constants used, which are compatible with values extracted from experiment and produced by other groups. We show that the decay <FONT FACE=Symbol>D ® p</FONT>N explains the relation <FONT FACE=Symbol>sD</FONT> < sigmaN.

Nucleon and delta sigma terms; Delta decay; Effective theories

Nucleon and delta sigma-terms

I. P. Cavalcante^I; M. R. Robilotta^II; J. Sá Borges^III; D. de O. Santos^I; G. R. S. Zarnauskas^II

^IDepto. de Física, CCET, Universidade Federal de Mato Grosso do Sul, C.P. 549, C.E.P. 79070-900, Campo Grande, MS, Brazil

^IIInstituto de Física, Universidade de São Paulo, C.P. 66318, 05315-970, São Paulo, SP, Brazil

^IIIUniversidade do Estado do Rio de Janeiro, Instituto de Física, Rua São Francisco Xavier, 524, Maracanã, Rio de Janeiro, RJ, Brazil

ABSTRACT

We evaluate nucleon and delta sigma-terms and obtain the results 43 MeV < s_N< 49 MeV and 28 MeV < s_D < 32 MeV, depending on the coupling constants used, which are compatible with values extracted from experiment and produced by other groups. We show that the decay D ® pN explains the relation s_D < s_N.

Keywords: Nucleon and delta sigma terms; Delta decay; Effective theories

I. INTRODUCTION

QCD is nowadays the main theoretical framework to describe hadronic interactions, but its non-Abelian character makes calculations in the low-energy regime unfeasible. In order to overcome this problem, one may work with either lattice QCD or effective field theories.

Effective theories are constructed by writing the most general Lagrangian containing all the terms allowed by the symmetries of the main theory. In the case of chiral symmetry, the various terms are organized considering the number of pion masses or derivatives of the pion field. This procedure gives meaning to the idea of chiral perturbation theory (ChPT). Considering only u and d quarks, we assume that the effective theory possesses approximate SU(2) × SU(2) chiral symmetry, broken by the small pion mass in the effective theory. An important aspect of chiral dynamics concerns the effects of this breaking of the symmetry over the nucleon and delta resonance masses. The answer to this question is related to sigma-terms.

The delta (D) plays a very important role in low-energy pion-nucleon (pN) scattering and correlated processes, such as the nucleon-nucleon interaction. When the delta is present, the scale of some amplitude denominators is given by the quantity w_D ~ M - m. Delta contributions are given by ratios of small quantities and may turn out to be large. In such cases, numerical values adopted for M - m do influence predictions produced by effective theories, especially those that rely on the small scale expansion [1] or the heavy baryon approximation [2].

In ChPT, there is a clear conceptual distinction between the bare baryon masses, present in the Lagrangian, and their respective observed values, which include loop corrections. The former should, in principle, be preferred as inputs in the evaluation of theoretical amplitudes. Nevertheless, as there is little information available concerning the bare delta mass, one tends to use physical values in calculations. In most cases, it is reasonable to expect that this would have little numerical importance. On the other hand, in the case of the parameter ø_D, which is a small quantity, the influence of loop corrections may become relatively large.

According to the Feynman-Hellmann theorem [3] the mass m_B of a baryon B is related to its sigma-term s_B by s_B = µ²d m_B/ dµ². Therefore the sigma-term provides a measure of the shift in the baryon mass due to chiral symmetry breaking. Whenever it is possible to evaluate s_B as a function of µ, the bare mass can be extracted from the relation

As the leading term in s_B is proportional to µ², the difference m_B-s_B provides a crude estimate for . In the case of the nucleon, one has s_N=45 MeV [4]. In ChPT, the leading contribution to s_N cannot be predicted theoretically. Formally, it is associated with the constant c₁ of the second order Lagrangian [5, 6], which can be extracted from empirical subthreshold information. The situation of the delta is much worse, for pD scattering data are not available. One is then forced to resort to models in order to calculate the delta sigma-term, which is associated with the parameter a₁ defined in ref. [1].

This paper is organized as follows. In section II we review our evaluation of the nucleon and delta sigma-terms, presented in [7] (the reader is referred to this paper for a detailed description of the work). In section III we show that the relation s_D < s_N is associated with the fact that the delta can decay. A brief summary is provided in section IV.

II. NUCLEON AND DELTA SIGMA-TERMS

Th nucleon sigma-term obtained by applying ChPT at O(q⁴) depends on the low-energy constants (LEC's) c₁, c₂ and c₃. In this work we review a model presented in [7, 8].

Data on pN subthreshold coefficients indicate that c₂ and c₃ are larger than c₁ and that their values are approximately saturated by D intermediate states [6]. Thus, up to O(q⁴), the function s_N(t) can be well represented by the leading tree contribution associated with c₁, supplemented by the two triangle diagrams shown in Fig.1, involving N and D intermediate states.

The nucleon scalar form factor in momentum space is defined by

where L_sb is the symmetry breaking term and t = (p¢-p)². In terms of the quark degrees of freedom, one has L_sb = - (u + d), with = (m_u + m_d)/2. The configuration space scalar form factor is denoted by _N and given by

with q = (p¢-p), in the Breit frame. The nucleon sigma-term, s_N, is given by

The contributions from the diagrams of Fig.1 to _N(r) read

where (r) and (r) denote contributions from diagrams with nucleon and delta as intermediate states, respectively.

In Fig.2, the condensed (QCD vacuum) and empty-space phases are represented by the horizontal lines at values 0 and 1, respectively, whereas the curve s_N represents the influence of the nucleon over the condensate. At a critical point R around 0.6 fm, this curve intersects the horizontal line at 1, indicating the possibility of a phase transition. We assume that this phase transition does take place at this point and that the condensate no longer exists in the region r < R.

For this reason, in our previous evaluation of s_N [7, 8], we used the expression

instead of eq. (4). This procedure is the basis of our model and is more extensively discussed in ref. [7].

In the numerical determination of s_N, we consider three possibilities for the pND coupling constant. The corresponding results, given in table 1, are quite close to the value extracted from experiment by Gasser, Leutwyler and Sainio [4], namely, s_N = 45 MeV.

The delta scalar form factor is defined as

where is the D spinor [9] and s_D and F_T are, respectively, the scalar and tensor form factors. The minus sign on the r.h.s. is associated with the conventions used in the free D Lagrangian as in ref. [1]. We assume that the scalar form factor is determined by a short range contact interaction and two long range two-pion processes as in the case of the nucleon.

The values of the distance R for which

_D(R)/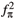µ² = 1 and the values of the delta sigma-term are given in table II, for different choices of the coupling constants g_pND and g_pDD. Results for the real component of s_D are sensitive to the coupling constant g_pDD and consistent with that given in ref. [10], namely s_D = (32 ± 3) MeV. On the other hand, our prediction is larger than that quoted in ref. [11].

The structure of partial contributions for SU(4) coupling constants, namely, g_pND = 1.33 and g_pDD = 0.75. is given in table III, where core and cloud refer to regions inside and outside the cutting radius R, respectively.

III. LOOP INTEGRALS

The results given in table III show that the difference between s_N and s_D is related to the cloud N contribution to s_D, which is rather small, compared to s_N. The reason for this behaviour is associated with the fact that the decay D ® pN is possible.

The decay D ® pN changes the behaviour of the loop integrals. In order to illustrate these changes and show the origin of the small size of the cloud N contribution to s_D, we present some details of how we deal with the loop integrals.

In the evaluation of the cloud N component of s_D, the following loop integral appears, among others:

where m_e and m_x are the external and the internal baryon masses, respectively. We employ the variables

where p and p¢ are the initial and final baryon momenta, respectively, whereas k and k¢ are the momenta of the exchanged pions.

The Feynman techniques for loop integration allow one to write the regular part of (8) as

with

In our calculational procedure we use configuration space expressions to obtain sigma-terms. Therefore, we need to perform Fourier transforms in the loop integrals,

with x = µr e k = q/µ.

Thus the configuration space equivalent for can be written as

where

and

The above integral can acquire an imaginary part. This fact becomes evident when we perform the integral in the variable b,

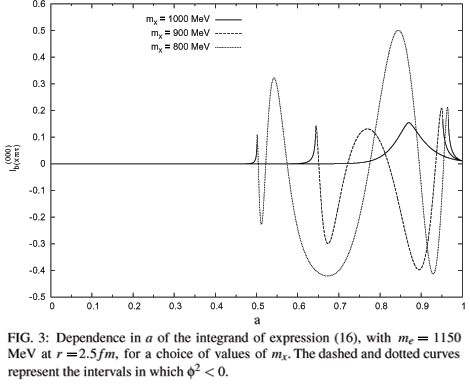
In general, when (µ + m_x) > m_e, the function f² is always positive. On the other hand, when (µ + m_x) < m_e, there is an interval in the integration variable a for which the function f² becomes negative. In case this happens, the functions K_l must be replaced by Y_l. The former are monotonic functions, whereas the latter oscillate and produce contributions with alternating signs inside the integrals. This kind of behaviour is illustrated in Fig. 3, for the arbitrary choices m_e = 1150 MeV, µ = 150 MeV. In this case the decay threshold corresponds to m_x = 1000 MeV.

This is the reason why the contributions in the case (µ + m_x) < m_e, which represents the fact that the external particle can decay, tend to be small. As this is a general feature of the Feynman diagrams, it happens whenever an unstable particle is present. One must bear in mind, however, that the size of this effect depends on both the coupling constants of the specific problem and on the gap m_e- m_x -µ. It is interesting to note that the importance of understanding the smallness of the delta sigma-term has been recently stressed in a conference talk by Meissner [12] and, to our knowledge, our paper is the only one proposing that the solution to this problem may be associated with the instability of the delta.

IV. SUMMARY

We have reviewed a model aimed at determining sigma-terms, which consists in cutting off configuration space expressions at the point where, as we assume, a phase transition occurs. Our main results are 43 MeV < s_N< 49 MeV and 28 MeV < s_D < 32 MeV, depending on the coupling constants employed. We have shown that the decay D ® pN changes the behaviour of loop integrals and gives rise to an oscillation in the cloud N contribution to s_D which is responsible for the relation s_D < s_N.

Acknowledgments

This work was supported by CNPq, FAPESP and FUNDECT/MS (Brazilian agencies).

[1] T. R. Hemmert, B. R. Holstein, and J. Kambor, J. Phys. G 24, 1831 (1998).

[2] N. Kaiser, S. Gerstendörfer, and W. Weise, Nucl. Phys. A 637, 395 (1998); N. Fettes and Ulf-G. Meissner, Nucl. Phys. A 693, 693 (2001).

[3] H. Hellmann, Einführung in die Quantenchemie (Deuticke Verlag, Leipzig, 1937); R.P. Feynman, Phys. Rev. 56, 340 (1939); S. T. Epstein, Am. J. Phys. 22, 613 (1954);

[4] J. Gasser, H. Leutwyler, and M. E. Sainio, Phys. Lett. B 253, 252 (1991); 253, 260 (1991).

[5] J. Gasser, M.E. Sainio, and A. Svarc, Nucl. Phys. B 307, 779 (1988).

[6] T. Becher and H. Leutwyler, Eur. Phys. Journal C 9, 643 (1999); JHEP 6, 17 (2001).

[7] I. P. Cavalcante, M. R. Robilotta, J. Sa Borges, D. de O. Santos, and G. R. S. Zarnauskas, Phys. Rev. C 72, 065207 (2005).

[8] M. R. Robilotta, Phys. Rev. C 63, 044004 (2001).

[9] C. Fronsdal, N. Cim. Suppl. 9, 416 (1958).

[10] V. E. Lyubovitskij, Th. Gutsche, A. Faessler, and E. G. Drukarev, Phys. Rev. D 63, 054026 (2001).

[11] V. Bernard, T. R. Hemmert, and Ulf-G. Meissner, Phys. Lett. B 622, 141 (2005).

[12] Ulf-G. Meissner, Proc. Sci. LATT2005, 009 (2005).

Received on 29 September, 2006

Publication Dates

• Publication in this collection
  24 Apr 2007
• Date of issue
  Mar 2007

History

• Received
  29 Sept 2006