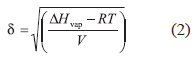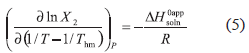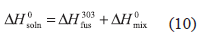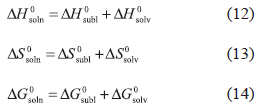Abstracts
Thermodynamic functions, Gibbs energy, enthalpy and entropy for the solution processes of ibuprofen (IBP) in acetone and dichloromethane (DCM) were calculated from solubility values obtained at temperatures ranging from 293.15 K to 313.15 K. The respective thermodynamic functions for mixing and solvation processes as well as the activity coefficients for the solute were calculated. IBP solubility was high and proved similar in both solvents but was greater in DCM than acetone. In addition, the thermodynamic quantities for the transfer process of this drug from cyclohexane to the organic solvents were also calculated in order to estimate the contributions of hydrogen-bonds or of other dipolar interactions. The results were discussed in terms of solute-solvent interactions.
Ibuprofen; Solubility; Transfer; Solution thermodynamics; Organic solvents
As funções termodinâmicas, energia de Gibbs, entalpia e entropia dos processos de solução de ibuprofeno (IBP) em acetona e em diclorometano (DCM) foram calculadas a partir dos valores de solubilidade, obtidos em intervalos de temperatura de 293,15 K a 313,15 K. As funções termodinâmicas respectivas para os processos de mistura e solvatação e os coeficientes de atividade para o soluto também foram calculados. A solubilidade do IBP foi grande e semelhante em ambos os solventes, mas, maior em DCM do que em acetona. Em adição, as quantidades termodinâmicas relativas ao processo de transferência desse fármaco do cicloexano para os solventes orgânicos foram, também, calculadas com o objetivo de estimar as contribuições devidas às ligações de hidrogênio ou a outras interações dipolares. Os resultados foram discutidos nos termos das interações soluto-solvente.
Ibuprofeno; Solubilidade; Transferência; Soluções termodinâmicas; Solventes orgânicos
ARTICLE
Thermodynamic study of the solubility of ibuprofen in acetone and dichloromethane
Diana Marcela Aragón; Jaiver Eduardo Rosas; Fleming Martínez* * Correspondence: F. Martinez. Sección de Farmacotecnia, Departamento de Farmacia, Universidad Nacional de Colombia, A.A. 14490 - Bogotá D.C. - Colombia. E-mail: fmartinezr@unal.edu.co
Sección de Farmacotecnia, Departamento de Farmacia, Universidad Nacional de Colombia
ABSTRACT
Thermodynamic functions, Gibbs energy, enthalpy and entropy for the solution processes of ibuprofen (IBP) in acetone and dichloromethane (DCM) were calculated from solubility values obtained at temperatures ranging from 293.15 K to 313.15 K. The respective thermodynamic functions for mixing and solvation processes as well as the activity coefficients for the solute were calculated. IBP solubility was high and proved similar in both solvents but was greater in DCM than acetone. In addition, the thermodynamic quantities for the transfer process of this drug from cyclohexane to the organic solvents were also calculated in order to estimate the contributions of hydrogen-bonds or of other dipolar interactions. The results were discussed in terms of solute-solvent interactions.
Uniterms: Ibuprofen. Solubility. Transfer. Solution thermodynamics. Organic solvents.
RESUMO
As funções termodinâmicas, energia de Gibbs, entalpia e entropia dos processos de solução de ibuprofeno (IBP) em acetona e em diclorometano (DCM) foram calculadas a partir dos valores de solubilidade, obtidos em intervalos de temperatura de 293,15 K a 313,15 K. As funções termodinâmicas respectivas para os processos de mistura e solvatação e os coeficientes de atividade para o soluto também foram calculados. A solubilidade do IBP foi grande e semelhante em ambos os solventes, mas, maior em DCM do que em acetona. Em adição, as quantidades termodinâmicas relativas ao processo de transferência desse fármaco do cicloexano para os solventes orgânicos foram, também, calculadas com o objetivo de estimar as contribuições devidas às ligações de hidrogênio ou a outras interações dipolares. Os resultados foram discutidos nos termos das interações soluto-solvente.
Unitermos: Ibuprofeno. Solubilidade. Transferência. Soluções termodinâmicas. Solventes orgânicos.
INTRODUCTION
Ibuprofen (IBP) is a non-steroidal anti-inflammatory drug. IBP also has analgesic and antipyretic action without producing addiction (Roberts II, Morrow, 2001). This drug is widely used in current therapeutics and is administered mainly by the peroral route as tablets, syrups and concentrates (Rosenstein-Ster, 2003).
Hydrophobic drug delivery systems based on techniques of microencapsulation have recently become a viable strategy. Microparticle systems are often prepared by emulsion techniques that include aqueous and organic phases; the drug solubility in each phase is an important value that needs to be determined for every microencapsulation study. Most microencapsulation techniques of hydrophobic drugs employ volatile organic solvent to dissolve the matrix polymer and where possible, to also dissolve the drug. Therefore, it is essential to determine the drug solubility in solvents such as acetone and dichloromethane. The results of these solubility studies form the basis of most considerations governing the choice of the appropriate microencapsulation technique (Tewes et al., 2006).
As a first stage towards a more thorough understanding of the molecular forces involved, the present work studied the thermodynamics of the solubility of IBP in two volatile organic solvents used for microencapsulation processes. This study was carried out with the key purpose of presenting more complete and systematic information on the properties of dissolution and transfer for this drug. The solubility at several temperatures was determined in acetone and dichloromethane as pure solvents, and the respective dissolution thermodynamic analysis was performed by using the Van't Hoff and Gibbs equations. Moreover, by using the values reported for the IBP fusion and sublimation processes, the contributions of the mixing and solvation processes to overall dissolution were also analyzed (Perlovich et al., 2004; Manrique, Martínez, 2007).
MATERIAL AND METHODS
Material
Ibuprofen USP (1994), acetone from A.R. Merck, dichloromethane A.R. (DCM) Merck and Millex®-13 mm filters, Millipore Corp were used in this study.
Solubility determinations
An excess of IBP was added to 20 mL of each organic solvent evaluated, in stoppered glass flasks. Solid-liquid mixtures were placed on a thermostatic mechanical shaker (Julabo SW23) kept at 313.15 ± 0.05 K for at least three days to reach equilibrium (this equilibrium time was established by quantifying the drug concentration until obtaining a constant value). Once at equilibrium, supernatant solutions were filtered (under isothermal conditions) to remove insoluble particles before composition analysis. Drug concentrations were determined by mass balance by weighing a specified quantity of the respective saturated solution and allowing solvent evaporation until a constant mass. After the procedures described above, the temperature was decreased by 5.0 K and stabilized at 308.15 K over at least two days, allowing the precipitation of the drug dissolved in excess and quantifying of the drug concentration in equilibrium. This procedure was repeated by decreasing the temperature in 5.0 K steps to reach 293.15 K. All experiments were performed at least three times and then averaged.
RESULTS AND DISCUSSION
The molecular structure of IBP and some of its physicochemical properties are summarized in Table I. The melting point, enthalpy of fusion, and enthalpy of sublimation were reported by Perlovich et al. (2004). This drug acts in solution mainly as a Lewis acid in order to establish hydrogen bonds with proton-acceptor functional groups of the solvents (oxygen in 0=C< and nitrogen in NC-). On the other hand, IBP can also act as a proton-acceptor compound by means of its carbonyl and hydroxyl moieties (Manrique, Martínez, 2007).
Ideal and experimental solubility of IBP
In a first approach, the ideal solubility of a crystalline solute in a liquid solvent can be calculated by Eq. (1):
where  is the ideal solubility of the solute in mole fraction, ΔHfus and ΔSfus are the molar enthalpy and entropy of fusion of the pure solute (at melting point), Tfus is the absolute melting point, T is the absolute solution temperature, and R is the gas constant (Manrique, Martínez, 2007).
is the ideal solubility of the solute in mole fraction, ΔHfus and ΔSfus are the molar enthalpy and entropy of fusion of the pure solute (at melting point), Tfus is the absolute melting point, T is the absolute solution temperature, and R is the gas constant (Manrique, Martínez, 2007).
Table II summarizes the experimental solubilities of IBP, expressed in mole fraction, in addition to the ideal solubilities calculated by means of Eq. (1) from ΔHfus, and Tfus presented in Table I. In almost all cases the coefficients of variation for experimental solubility were less than 1.0%.
As shown in Table II, the IBP solubilities in both volatile solvents were greater than those obtained in other organic solvents (Garzón, Martínez, 2004). Similarly, it is interesting to note that IBP solubility was greater than drug ideal solubility at all temperatures tested (except for acetone at 313.15 K), where these values proved greater in DCM than in acetone. Thus, it is evident that the highest solubility value in mole fraction for IBP was obtained in DCM at 313.15 K, while the lowest value was found in acetone at 293.15 K. Unfortunately, no previous reports on solubility of IBP in these solvents are available, and therefore no direct comparison is possible.
IBP solubility analysis in terms of solubility parameters
Although experimental solubility is a complex phenomenon, definitions have been proposed in order to explain this important physicochemical property of drugs. One of these was proposed by Hildebrand et al. (1970) in terms of the solubility parameter, δ, which is defined as the square root of cohesive energy density, and is calculated according to Eq. (2):
where, ΔHvap is the vaporization enthalpy and V is the molar volume. Hildebrand solubility parameters were initially proposed for nonpolar compounds interacting among them by dispersion forces (London forces). Nevertheless, IBP and almost all the solvents investigated, interact by London forces and also by other more energetic forces, namely, dipolar forces and hydrogen-bonding. In this context, Hansen (1967) split the general δ values into three partial parameters representing the respective contributions by dispersive forces δd, dipolar forces δp, and hydrogen-bonding δh. These subparameters are related to total solubility parameter δT, as follows:
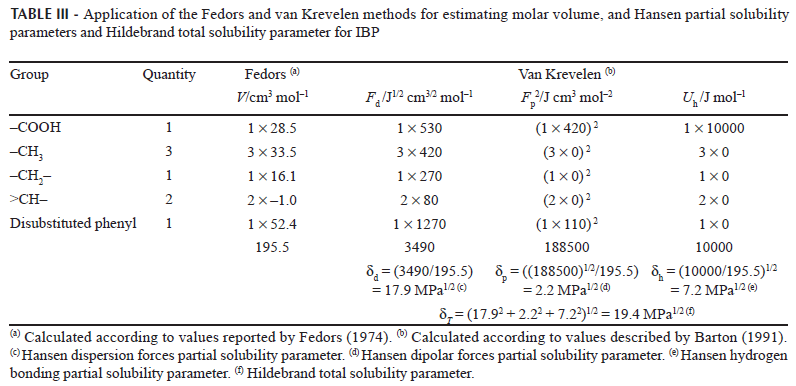
The experimental determination of partial solubility parameters is not straight forward and therefore some calculus methods based on the contribution of groups have been described. The most common methods are those proposed by Fedors and van Krevelen (Barton, 1991). Table III summarizes IBP solubility parameters, demonstrating that the London forces are the most relevant for this compound, which could be attributed mainly to phenyl and methyl moieties. Thus, based on the δT value (19.4 MPa1/2), IBP could be considered a semipolar compound. On the other hand, according to the literature (Martin, Bustamante, 1989; Martin et al., 1993), the greatest drug solubility value should be found in solvents which have similar δ values. Accordingly, Table IV also summarizes the δ values for the organic solvents tested (Barton, 1991).
Apparently, some similarity across all δ values is evident on comparing IBP and the solvents tested (Tables III and IV), in particular for δT, δd and δh, although no similarity was found for δp. This fact demonstrates that the solubility of drug compounds is a more complex phenomenon than that described solely by solubility parameters without considering other physicochemical properties of solvents and solutes.
IBP activity coefficients
The solute activity coefficient in the solution (γ2) is calculated as  /X2 and is an indication of the deviation presented by IBP from its ideal behavior (Manrique, Martínez, 2007). Table V shows activity coefficients as a function of temperature. Again, it is interesting to note that γ2 values for both solvents are lower than unit values (except in acetone at 313.15 K) and increase with rises in temperature, apparently indicating a more ideal drug solution behavior at increasing temperatures.
/X2 and is an indication of the deviation presented by IBP from its ideal behavior (Manrique, Martínez, 2007). Table V shows activity coefficients as a function of temperature. Again, it is interesting to note that γ2 values for both solvents are lower than unit values (except in acetone at 313.15 K) and increase with rises in temperature, apparently indicating a more ideal drug solution behavior at increasing temperatures.
From the γ2 values presented in Table V, an approximate estimation of solute-solvent intermolecular interactions can be made based on the following expression:
where w11, w22 and w12 represent the solvent-solvent, solute-solute and solvent-solute interaction energies, respectively; V2 is the molar volume of the supercooled liquid solute, and finally, Φ1 is the volume fraction of the solvent. In a first approach, the term (V2Φ12/RT)T,P may be considered approximately constant at the same temperature, and then γ2 depends almost exclusively on w11, w22 and w12 (Kristl, Vesnaver, 1995). While the term w12 term favors the solution process, both w11 and w22 terms are unfavorable for solubility. The contribution of w22 represents the work necessary to transfer drug molecules from the solid to the vapor state and is therefore constant in both organic solvents.
Both tested solvents are volatile and have low solubility parameters, which imply low w11 values, whereas w22 value is also relatively low, based on ΔHfus and Tfus values (Table I). For these reasons, in order to obtain γ2 values near to unit values, large w12 values would also be required for this drug in these solvents.
Thermodynamic functions of solution
According to Van't Hoff analysis, the apparent standard enthalpy change of solution is obtained from the slope of ln X2 vs. 1/T plot (Garzón, Martínez, 2004). Nevertheless, in recent thermodynamic treatments some modifications have been introduced in the Van't Hoff equation in order to diminish the propagation of uncertainties and consequently to separate the chemical effects from those due to statistical treatments used when enthalpy-entropy compensation plots are constructed. Hence, the mean harmonic temperature (Thm) is used in the Van't Hoff analysis. Thm is calculated as n/ (1/T), where n is the number of temperatures studied (Krug et al., 1976). In the present case, the Thm value obtained is only 303 K. The modified, more widely used expression is the following (Bustamante et al., 1998):
(1/T), where n is the number of temperatures studied (Krug et al., 1976). In the present case, the Thm value obtained is only 303 K. The modified, more widely used expression is the following (Bustamante et al., 1998):
The modified Van't Hoff plot for IBP in the solvents tested is presented in Figure 1. In general, linear regression models with good determination coefficients were obtained in both cases studied.
The apparent standard free energy change for the solution process  , considering the approach proposed by Krug et al. (1976) is calculated by:
, considering the approach proposed by Krug et al. (1976) is calculated by:
in which, the intercept used is the one obtained in the analysis by treatment of ln X2 as a function of 1/T - 1/Thm. Finally, the standard entropi c change for the solution process ΔS0soln is obtained from the respective ΔH0soln and ΔG0soln values by using:
Table VI summarizes the apparent standard thermodynamic functions for the experimental solution process of IBP in the organic solvents investigated, including those functions for the ideal process. In order to calculate the thermodynamic magnitudes of experimental solution processes, some methods to calculate uncertainties propagation, were used (Bevington, 1969). In particular, the total uncertainties were obtained as the square root of the sum of the individual uncertainties squared. The standard free energy of solution was found to be positive in all cases; i.e., the solution process apparently is not spontaneous, which may be explained in terms of the concentration scale used (mole fraction), where the reference state is the ideal solution having the unit as concentration of IBP (the solid pure solute). On the other hand, it is noteworthy that all the solution thermodynamic quantities in acetone are similar to those obtained for the ideal solution process.
With the aim of comparing the relative contributions of enthalpy (%ζH) and entropy (%ζTS) to the solution process, equations (8) and (9) were employed, respectively (Perlovich et al., 2004):
From Table VI, it follows that in all cases the solution enthalpy contributes to a greater extent to Gibbs energy of the IBP solution processes, than does the solution entropy. Interestingly, enthalpy and entropy contributions for both solvents are almost equal to those obtained for the ideal solution process.
Thermodynamic functions of mixing
It is well known that the solution process may be represented by the following hypothetical stages (Manrique et al., 2008):
Solute(Solid) Solute(Liquid)
Solute(Liquid) Solute(Solution)
Solute(Solution)
where, the respective partial processes involved in drug dissolution are solute fusion and mixing at the same temperature (303 K), which permits calculation of the partial thermodynamic contributions to the overall solution process by means of equations (10) and (11), respectively.
where,  and
and  represent the thermodynamic functions of the fusion process at the harmonic temperature (303 K). Nevertheless, for practical purposes,
represent the thermodynamic functions of the fusion process at the harmonic temperature (303 K). Nevertheless, for practical purposes,  and
and  values (Table VI) were used instead of
values (Table VI) were used instead of  and
and  as has been done previously in other studies (Manrique, Martínez, 2007; Manrique et al., 2008; Triana et al., 2009). The thermodynamic functions of mixing of IBP are summarized in Table VII.
as has been done previously in other studies (Manrique, Martínez, 2007; Manrique et al., 2008; Triana et al., 2009). The thermodynamic functions of mixing of IBP are summarized in Table VII.
The partial contributions of ideal solution (related to solute fusion process) and mixing processes to the enthalpy and entropy of drug solution, shows that  and
and  are positive (Table VI), whereas the contribution of the thermodynamic functions relative to the mixing process to the solution process is negative. It can be concluded that the solution process of this drug in these solvents is driven by the solution entropies and by the mixing enthalpies (based on the positive ΔS0soln values presented in Table VI and the negative ΔH0mix values presented in Table VII).
are positive (Table VI), whereas the contribution of the thermodynamic functions relative to the mixing process to the solution process is negative. It can be concluded that the solution process of this drug in these solvents is driven by the solution entropies and by the mixing enthalpies (based on the positive ΔS0soln values presented in Table VI and the negative ΔH0mix values presented in Table VII).
The net variation in ΔH0mix values results from the contribution of several kinds of interactions. The enthalpy of cavity formation (required for solute accommodation) is endothermic because energy must be supplied against the cohesive forces of the solvent. This process decreases solubility. On the other hand, the enthalpy of solute-solvent interaction is exothermic and results mainly from van der Waals and Lewis acid-base interactions. Thus, the negative values obtained for enthalpy and entropy of mixing for IBP in both solvents, could indicate that the hydrogen bonds established between IBP and these solvents are much greater than the solvent-solvent intermolecular interactions, which leads to energy release during the mixing processes.
Thermodynamic functions of solvation
In addition to the hypothetic fusion-mixing stages outlined previously, the solution process may also be represented by the following hypothetical stages (Manrique et al., 2008):
Solute(Solid) Solute(Vapor)
Solute(Vapor) Solute(Solution)
Solute(Solution)
where, the respective partial processes contributing to the solution process, are in this case, sublimation and solvation. This treatment allows calculation of the partial thermodynamic contributions to the solution process by means of equations (12) and (13), respectively, while the Gibbs energy of solvation is calculated using equation (14):
where, ΔH0sobl = 115.8 kJ mol-1 was taken from Perlovich et al. (2004) and therefore, the function ΔH0solv was calculated from ΔH0soln values presented in Table VI. The respective Gibbs energy (ΔG0sobl = 43.1 kJ mol-1) and entropy of sublimation (ΔS0sobl = 240.1 J mol-1 K-1) at 303 K were taken from the literature (Manrique, Martínez, 2007). The thermodynamic functions of solvation are presented in Table VIII, whereas to compare the relative contributions of enthalpy (%ζH) and entropy (%ζTS) to the solvation process, two equations analogous to equations (8) and (9) were employed.
Based on the values of %ζH and %ζTS presented in Table VIII, it follows that the main contributing force to standard Gibbs energy of the solvation process of IBP in the volatile solvents tested is enthalpy (%ζH are greater than 62%).
On the other hand, because not only the main driving force of solvation process of drug compounds is important, but also the balance between specific and non-specific solute-solvent interactions, some parameters which describe the relative ratio of specific and non-specific solute-solvent interaction in terms of enthalpies (%εH) and entropies (%εS), were used according to the following definitions introduced by Perlovich et al. (2004):
where ΔH0spec = ΔH0soln(Org) - ΔH0soln(CH) = ΔH0soln(CH→Org), ΔH0non-spec = ΔH0soln(CH) - ΔH0subl = ΔH0solv(CH), ΔS0spec = ΔS0soln(ORg) - ΔS0soln(CH) = ΔS0(CH→Org), and finally, ΔS0non-spec = ΔS0soln(CH).
Cyclohexane (CH) was chosen as an "inert" solvent, which interacts with drug molecules solely by non-specific interactions (dispersion forces), while the volatile solvents tested interact with IBP through specific interactions such as hydrogen bonding or other dipole-dipole forces. Solution thermodynamic quantities of IBP in cyclohexane at 303 K are ΔG0soln(CH) = 4.75 kJ mol-1, ΔH0soln(CH) = 49.4 kJ mol-1, and ΔS0soln(CH) = 147.4 (Garzón, Martínez, 2004; Manrique, Martínez, 2007). The %εH and %εS values for IBP solvation are also shown in Table VIII. These values indicate that during dissolution of IBP in the solvents studied, the specific solute-solvent interactions (chiefly hydrogen bonding) effectively affect the entropic term of Gibbs energy with respect to non-specific interactions, in particular in DCM (%εS  71%). With regard to the enthalpic term, the non-specific solute-solvent interactions dominate in both solvents because it is lower than 51%. The results obtained for the last properties of this drug in both tested solvents, are different in magnitude to those obtained in other organic solvents with different hydrogen bonding capability (Garzón, Martínez, 2004), although the reasons for this behavior are unclear.
71%). With regard to the enthalpic term, the non-specific solute-solvent interactions dominate in both solvents because it is lower than 51%. The results obtained for the last properties of this drug in both tested solvents, are different in magnitude to those obtained in other organic solvents with different hydrogen bonding capability (Garzón, Martínez, 2004), although the reasons for this behavior are unclear.
Apparent thermodynamic functions of IBP transfer from cyclohexane to other organic solvents
In order to contribute with the generation and systematization of thermodynamic quantities of transfer, useful in QSAR studies, as well as in novel pharmaceutical dosage forms design, these values were calculated for the transfer of IBP from CH to the volatile organic solvents tested.
Table IX depicts Gibbs energy, enthalpy and entropy of transfer including the respective %ζH and %ζTS values. The thermodynamic quantities were calculated as the difference between the IBP solution functions in the organic solvents (Table VI) and those for CH presented in the literature (Garzón, Martínez, 2004; Manrique, Martínez, 2007). According to Table IX, the transfer process of this drug from CH to both volatile organic solvents is spontaneous ΔG0CH → Org<0 and driven by enthalpy ΔH0CH → Org<0. On the other hand, the enthalpy and the entropy contribute in similar proportions to the transfer process although the contribution is slightly greater for enthalpy (%ζH  51.5%).
51.5%).
In the net drug transfer process between hydrocarbons and organic solvents with hydrogen-bonding capability as donors or acceptors or other dipole-dipole interactions, the enthalpic and entropic changes imply energetic requirements and the molecular randomness (increase or decrease in the molecular disorder), respectively. In general terms, the behavior presented in each phase should be considered independently, before and after the transfer process.
Since hypothetically the solute is initially present only in the hydrocarbon phase, then the generation of a cavity in the dipolar organic medium in order to accommodate the solute after the transfer process is required. This is an endothermic phenomenon, since an energy supply is necessary to overcome the solvent-solvent interaction of dipolar organic solvent molecules. When the solute molecules are accommodated in the dipolar organic phase, a quantity of energy is released, mainly due to formation of hydrogen bonds (or other dipolar interactions) between the molecules of the drug and the solvent.
On the other hand, after a certain number of solute molecules have migrated from the hydrocarbon to the dipolar organic phase to achieve hypothetical equilibrium, the original cavities occupied by the drug in the hydrocarbon phase become occupied by CH molecules. This event produces an energy release due to CH-CH interactions. Thus, the negative enthalpy values of transfer obtained could be explained by strong interactions due to hydrogen-bonding (or other dipolar interactions) among IBP and the dipolar solvents, which also diminish entropy by drug immobilization within these solvents.
CONCLUSIONS
Based on the topics discussed above it can be concluded that the solution process of IBP in the volatile organic solvents studied is complex and depends on the nature of the solvent. Finally, the data presented in this report contributes to the body of physicochemical information available on the solubility of this extensively used anti-inflammatory drug.
ACKNOWLEDGMENTS
We would like to thank the DIB of the Universidad Nacional de Colombia (UNC) for the financial support. Additionally, we extend our thanks to the Department of Pharmacy of UNC for assisting with the equipment and laboratories used.
Received for publication on 04th March 2009
Accepted for publication on 13th May 2009
- BARTON, A. Handbook of solubility parameters and other cohesion parameters 2.ed. New York: CRC Press, 1991. p.157-193.
- BEVINGTON, P. R. Data reduction and error analysis for the physical sciences New York: McGraw-Hill Book, Co., 1969. p.56-65.
- BUDAVARI, S.; O'NEIL, M. J.; SMITH, A.; HECKELMAN, P. E.; OBENCHAIN JR, J. R.; GALLIPEAU, J. A. R.; D'ARECEA, M. A. The Merck Index: an encyclopedia of chemicals, drugs, and biologicals. 13.ed. Whitehouse Station: Merck & Co., Inc., 2001. p.876.
- BUSTAMANTE, P.; ROMERO, S.; PEÑA, A.; REILLO, A. Enthalpy-entropy compensation for the solubility of drugs in solvent mixtures: Paracetamol, acetanilide, and nalidixic acid in dioxane-water. J. Pharm. Sci., v.87, n.12, p.1590-1596, 1998.
- FEDORS, R. F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci, New York, v.14, n.2, p.147-154, 1974.
- GARZÓN, L. C.; MARTÍNEZ, F. Temperature-solubility dependence for ibuprofen in some organic and aqueous solvents. J. Solution Chem., v.33, n.11, p.1379-1395, 2004.
- HANSEN, J. M. The three dimensional solubility parameter and solvent diffusion coefficient. Importance in surface coating formulation Copenhagen: Danish Technical Press, 1967. 106 p. [Ph.D. Thesis. College of Advanced Technology]
- HILDEBRAND, J. H.; PRAUSNITZ, J. M.; SCOTT, R. L. Regular and related solutions. New York: Van Nostrand Reinhold, 1970. 228 p.
- KRISTL, A.; VESNAVER, G. Thermodynamic investigation of the effect of octanol-water mutual miscibility on the partitioning and solubility of some guanine derivatives. J. Chem. Soc. Faraday Trans., v.91, n.6, p.995-998, 1995.
- KRUG, R. R.; HUNTER, W. G.; GRIEGER, R. A. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistical effects. J. Phys. Chem., Washington, v.80, n.21, p.2341-2351, 1976.
- MANRIQUE, J.; MARTÍNEZ, F. Solubility of ibuprofen in some ethanol + water cosolvent mixtures at several temperatures. Lat. Am. J. Pharm., v.26, n.3, p.344-354, 2007.
- MANRIQUE, Y. J.; PACHECO, D. P.; MARTÍNEZ, F. Thermodynamics of mixing and solvation of ibuprofen and naproxen in propylene glycol + water cosolvent mixtures. J. Solution Chem., New York, v.37, n.2, p.165-181, 2008.
- MARTIN, A.; BUSTAMANTE, P. El parámetro de solubilidad en las ciencias farmacéuticas. Anal. Real Acad. Farm, Madrid, v.55, n.2, p.175-202, 1989.
- MARTIN, A.; BUSTAMANTE, P.; CHUN, A. H. C. Physical pharmacy: physical chemical principles in the pharmaceutical sciences.4.ed. Philadelphia: Lea & Febiger, 1993. p.223-227.
- PERLOVICH, G. L.; KURKOV, S. V.; HANSEN, L. K.; BAUER-BRANDL, A. Thermodynamics of sublimation, crystal lattice energies, and crystal structures of racemates and enantiomers: (+)- and (+/-)-ibuprofen. J. Pharm. Sci, Washington, v.93, n.3, p.654-666, 2004.
- ROBERTS II, L. J.; MORROW, J. D. Analgesic-antipyretic and anti-inflammatory agents and drugs employed in the treatment of gout. In: HARDMAN, J. G.; LIMBIRD, L. E.; GILMAN, A. G. (Eds.). Goodman & Gilman's. The Pharmacological basis of therapeutics. 10.ed. New York: McGraw-Hill, 2001. p.703-705.
- ROSENSTEIN-STER, E. Diccionario de especialidades farmacéuticas. 32.ed. Bogotá: Thompson P. L. M., S. A., 2004. p.553-554.
- TEWES, F.; BOURY, F.; BENOIT, J. P. Biodegradable microspheres: Advances in production technology. In: BENITA, S. (Ed.). Microencapsulation: Methods and industrial applications. 2.ed. New York: Taylor & Francis Group, LLC, 2006. p.1-53.
- TRIANA, M. T.; REYES, A. C.; JIMENEZ-KAIRUZ, A. F.; MANZO, R. H.; MARTÍNEZ, F. Solution and mixing thermodynamics of propranolol and atenolol in aqueous media. J. Solution Chem., New York, v.38, n.1, p.73-81, 2009.
- UNITED STATES PHARMACOPEIA. 23.ed. Rockville: United States Pharmacopeial Convention, 1994. p.785-786.
Publication Dates
-
Publication in this collection
17 Aug 2010 -
Date of issue
June 2010
History
-
Received
04 Mar 2009 -
Accepted
13 May 2009