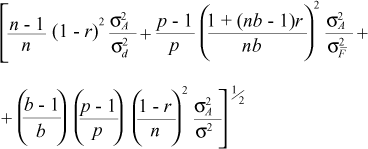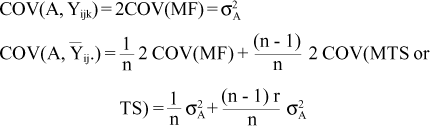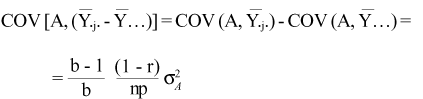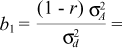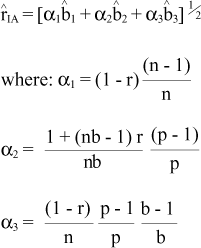Abstracts
The components of genetic variation and genetic gain obtained with three selection methods - individual, combined and multi-effect index selection - were compared in rubber tree [Hevea brasiliensis (Willd. ex Adr. de Juss.) Muell. Arg.] progenies. The rubber tree is a cross pollinating species with a mixed reproductive system in which the self pollination rate is 22%. Twenty-two half sib progenies were planted at experimental stations at Pindorama, Votuporanga and Jaú, in São Paulo State, using a randomized and complete block design, with five replications and ten plants per plot. Dry rubber production was assessed when the plants were three years old. Based on the genetic variability of the populations, Pindorama was the best environment for the expression of variability. At the individual level, heritability was seriously affected when random progenies from an open pollinating population were considered as half sib progenies. Considerable overestimation of genetic gains occurred during individual, combined and multi-effect index selection when the rubber tree reproductive system was not considered as mixed. Selection based on the multi-effect index maximizes genetic progress and should be used more in rubber tree breeding programs.
O presente trabalho objetivou comparar os componentes da variação genética e ganho genético obtidos através da seleção individual, combinada e pelo índice multi-efeitos em progênies de seringueira [Hevea brasiliensis (Willd ex Adr. de Juss.) Müell. Arg.], considerando-a como espécie alógama e de sistema reprodutivo misto, com taxa de aufecundação de 22%. Vinte e duas progênies de meio-irmãos foram plantadas nas Estações Experimentais de Pindorama, Votuporanga e Jaú, no estado de São Paulo, no delineamento de blocos ao acaso, com cinco repetições e dez plantas por parcela. Aos três anos de idade o caráter produção de borracha seca foi avaliado. Os resultados demonstraram haver variabilidade genética nas populações, bem como caracterizaram Pindorama como um ambiente mais propício para a expressão da referida variabilidade. As herdabilidades ao nível de indivíduos são consideravelmente afetadas ao assumir progênies de polinização aberta como sendo de meio-irmãos. Superestimativas consideráveis de ganhos genéticos ocorrem na seleção individual, combinada e índice multi-efeitos, quando não se considera o sistema reprodutivo misto para a seringueira. A seleção com base no índice multi-efeitos maximiza o progresso genético e deve ser utilizada.
METODOLOGY
Selection and genetic gain in rubber tree (Hevea) populations using a mixed mating system
Reginaldo Brito da Costa1, Marcos Deon Vilela de Resende2, Antonio José de Araujo3, Paulo de Souza Gonçalves4 and Antonio Rioyei Higa3
12EMBRAPA - Centro Nacional de Pesquisa de Florestas (CNPF), Caixa Postal 319, 83411-000 Colombo, PR, Brasil.
3Departamento de Silvicultura e Manejo,Universidade Federal do Paraná (UFPR), Caixa Postal 886, 80001-970 Curitiba, PR, Brasil.
4Programa Seringueira, Centro de Café e Plantas Tropicais, Instituto Agronômico de Campinas (IAC), Caixa Postal 28, 13001-970 Campinas, SP, Brasil.
Send correspondence to P.S.G. E-mail: paulog@cec.iac.br
ABSTRACT
The components of genetic variation and genetic gain obtained with three selection methods - individual, combined and multi-effect index selection - were compared in rubber tree [Hevea brasiliensis (Willd. ex Adr. de Juss.) Muell. Arg.] progenies. The rubber tree is a cross pollinating species with a mixed reproductive system in which the self pollination rate is 22%. Twenty-two half sib progenies were planted at experimental stations at Pindorama, Votuporanga and Jaú, in São Paulo State, using a randomized and complete block design, with five replications and ten plants per plot. Dry rubber production was assessed when the plants were three years old. Based on the genetic variability of the populations, Pindorama was the best environment for the expression of variability. At the individual level, heritability was seriously affected when random progenies from an open pollinating population were considered as half sib progenies. Considerable overestimation of genetic gains occurred during individual, combined and multi-effect index selection when the rubber tree reproductive system was not considered as mixed. Selection based on the multi-effect index maximizes genetic progress and should be used more in rubber tree breeding programs.
INTRODUCTION
The rubber tree [Hevea brasiliensis (Willd ex Adr. de Juss.) Muell. Arg.] is considered a preferentially cross pollinating, perennial species, with a long breeding cycle. Usually, three selection stages are involved and 25 to 30 years are required until the final choice of clones for large scale planting can be made (Gonçalves et al., 1988). This long breeding process has led to considerable investment in studies of genetic parameters to maximize the selection progress. Of particular interest to breeders are the genetic variance, heritability and gains provided by different selection methods.
Studies on genetic variation have been carried out in Malaysia (Nga and Subramanian, 1974; Tan et al., 1975; Tan and Subramanian, 1976; Tan, 1977, 1978a,b) and Nigeria (Alika and Onokpise, 1982; Alika, 1985). In Brazil, studies on the heritability of various traits have been done by Siqueira (1978), Valois et al. (1978), Paiva et al. (1982, 1983), Gonçalves et al. (1990, 1992, 1996), Moreti et al. (1994) and Boock et al. (1995).
These studies have considered the rubber tree as an open pollinating species. Simmonds (1989), however, reported an average self pollination rate of 22% with an estimated amplitude of 16-28%. More recently, Paiva (1992) obtained a mean inbreeding rate above 20% in natural populations. These findings identify the rubber tree as a species with a mixed reproductive system.
The assumption that the covariance among individuals within the progeny (COVp) of an open pollination population in a forest ambient corresponds to 25% of the additive genetic variance (s2A) usually leads to an overestimation of this variance. Consequently, the heritability coefficient and genetic gains from selection are equally overestimated (Squilace, 1974; Namkoong, 1981). This occurs because some species allow a certain rate of self pollination, which normally increases the covariance among individuals in the progeny. In addition, use of the relationship s2A = 4 COVp results in the overestimation of additive variance (Resende et al., 1995b).
This situation is typical of Eucalyptus species, which have rates of self pollination ranging from 8 to 40%. Moran and Bell (1983) and Griffin et al. (1987) considered Eucalyptus species to have a mixed reproductive system.
Adoption of the model presented by Cockerham and Weir (1984) for species with a mixed reproductive system allows better characterization of the genetic structure of such populations. This practice provides a more suitable definition of the components of genetic variation and, consequently, of the effects of self pollination in estimating genetic parameters (Resende et al., 1995b, 1996). In addition, the considerations presented by Namkoong (1966) and Squilace (1974) were based only on additive genetic variance, and did not consider the other components of genetic variation which occur where there is inbreeding.
Thus, any recommendations on how to choose the genetic material for large scale planting should take into consideration the variability associated with a mixed reproductive system, which, in the case of the rubber tree, includes the self pollination rate.
In the present study, the genetic variation and genetic gain associated with individual, combined and multi-effect index selection in rubber tree progenies were compared, assuming an open pollinating species with a mixed reproductive system.
MATERIAL AND METHODS
The genetic material used consisted of 22 progenies of half sibs from open pollinated seeds, obtained from 22 parent clones selected phenotypically from an H. brasiliensis population composed of material of Asian origin introduced to Instituto Agronômico de Campinas (IAC) in 1952.
The progeny tests were set up at three experimental stations belonging to IAC in São Paulo State. The characteristics of these localities are described below.
a) Jaú experimental station: latitude 22o17'S, longitude 48o34'W and altitude of 580 m. The soil is clay textured dark red latosoil deep and flat with a well-drained topography. An Aw (Köppen) climate predominates in this region, with a defined dry season, annual mean temperature of 21.6°C, average humidity of 70% with extremes of 77% in February and 59% in August. The mean annual rainfall is 1,344 mm.
b) Pindorama experimental station: latitude 21o13'S, longitude 48o56'W and altitude of 560 m, with red-yellow podzolic soil of medium texture which was TB eutrophic, deep, abrupt and well drained (Lepsch and Valadares, 1976). The climate is tropical continental, with a wet summer and a dry winter period with reduced temperatures and rainfall. The mean annual temperature is 22.2°C, with a maximum of 28.9°C and a minimum of 16.6oC. The mean annual rainfall is 1,390 mm. The period from October to April usually has a favorable precipitation for growth and production. Low precipitation and temperatures occur from May to September.
c) Votuporanga experimental station: latitude 20o25'S, longitude 49o50'W and altitude of 450 m. The soil is podzolic sandy phase type and the climate tropical continental, with a hot, wet summer and a cool, dry winter period with low temperatures and rainfall. The mean annual temperature is 22.3°C and the mean annual rainfall is 1,420 mm.
The seeds were collected at the IAC experimental center, then germinated in polyethylene bags, at the three experimental stations and taken to their definitive locations when they showed two leaf umbrellas. The seedlings were set out in a randomized complete block design with 22 treatments, five replications and ten plants per plot (1.5 m x 1.5 m) in single rows. The progenies were assessed for rubber production when they were three years old.
Dry rubber production (RP) was determined by the Hamaker-Morris-Mann (HMM) test modified for three-year-old seedlings (Tan and Subramanian, 1976) using the mean dry rubber production from three cuts per plant. The tapping panel was opened 20 cm from the soil, using the 1/2S d/3 system, with a total of 35 cuts. The first five samples, which corresponded to the "breaking in of the panel" stage, were discarded. The term 1/2S corresponded to the half spiral cut and the term d/3 expressed the interval between tappings, i.e., tapping three days.
The analysis using the statistical model below considered all variables (except the mean) as random effects.
Yijk = m + pi + bj + eij + dijk
where Yijk = observed value of the kth plant in the jth replication within the ith progeny, m = general mean, pi = effect of the ith progeny (i = 1, 2,...22), bj = effect of the jth replication (j = 1, 2, ..3), eij = experimental error associated with the ijth plot and dijk = effect of the kth plant within the ijth plot.
Estimates of the genetic and phenotypic parameters were obtained using the SELEGEN genetic statistical software developed by Resende et al. (1994).
Heritability coefficients at the individual within plot level (h2d), progeny mean (h2f), plot mean (h2p), individual within blocks (h2ib) and individual plants (h2ie) associated with the different effects of the linear model, were estimated by the following expressions (Resende and Higa, 1994).
where s2A = 4s2p, s2A = additive genetic variance, s2e = among plots environmental variance, s2d = among plants within plots phenotypic variance, s2p = among progenies genetic variance, n = number of plants/plot and b = number of blocks.
The coefficients of genetic (CVg%) and experimental (CVe%) variation were estimated using the following formulas presented by Vencovsky (1987):
Estimates of the genetic values and the genetic progress were obtained by individual (Ii), combined (Ic) or multi-effect (Ime) index selection in a univariate situation, using the expressions described by Resende and Higa (1994):
where h2ie is the heritability coefficient in the restricted sense at the individual level in the experiment, Xijk is the value of the kth of the individual in the ijthplot,  is the general experimental mean, Xi.. is the progeny mean,
is the general experimental mean, Xi.. is the progeny mean,  ij.. is the plot mean, Xijk is the deviation of the individual value (plot) and
ij.. is the plot mean, Xijk is the deviation of the individual value (plot) and  is the block mean.
is the block mean.
The progress with combined selection was equivalent to the mean of the genetic values (index) of the selected individuals. Selection by the multi-effect index was based on the product of the individual phenotypic value, plot mean, progeny mean, block mean and the general mean of the experiment using the index weighting coefficients. The method reduced the weight attributed to the general family means thus allowing a better distribution of selected individuals in the various families.
The index weighting coefficients were determined to maximize the correlation between the index and the genetic value. This maximization was obtained by regressing the genetic value on the phenotypic values, which lead to a matrix system (Henderson, 1963).
The following accuracy estimators derived by Resende et al. (1995a) for the different selection methods were used:
a) Individual:
b) Combined selection:
c) Multi-effect index:
where s2F = genotypic variance at the mean progeny level, s2Fie = phenotypic variance at the individual level, s2 = residual variance at the plot level, r = genetic correlation coefficient among individuals of a single progeny (1/4 for half sibs) and n, b, p = number of plants per plot, block and progeny, respectively (see appendix).
The accuracy parameter is a very useful measurement of the precision of the genetic values predicted and it corresponds to the correlation between the true and the predicted genetic values.
The genetic parameters obtained were also estimated using the SELEGEN software (Resende et al., 1994) for the dry rubber production trait by adopting a model for a species with a mixed reproduction system, and a self pollination rate of 22%. The models were considered complete (0.155 kinship coefficient) and additive (0.18 kinship coefficient) as defined by Resende et al. (1995b).
The complete model considered the additive genetic merit of the individuals and the dominance deviations. The additive model only considered the additive genetic merit of the individuals, i.e., the variation in genetic values was attributed to an additive effect of the genes.
The genetic model adopted corresponded to that presented by Cockerham and Weir (1984):
where F = the endogamy coefficient; Fc = two loci joint endogamy coefficient, equivalent to
s
2A2D12 2RESULTS AND DISCUSSION
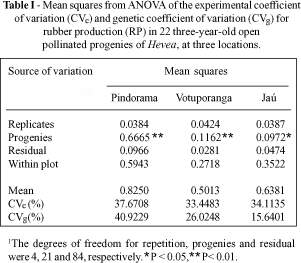
Table I shows the analysis of variance for RP. Significant among-family differences were detected by the F test. This variability was an essential condition for establishing a genetic breeding program and it could be effectively exploited to increase rubber production.
The experimental coefficients of variation (CVe%) obtained for RP at Pindorama (37.7%), Votuporanga (33.5%) and Jaú (43.1%) indicated that this trait is subject to great experimental errors. However, these values agree with similar estimates by Paiva et al. (1982) and Alves et al. (1987) who obtained CVe% of 38.3% and 50.4%. The levels were similar to those reported by Moreti et al. (1994).
The genetic variation coefficient, which expresses the amount of existing genetic variation as a percentage of the general mean, was higher at Pindorama (40.9%) than at Votuporanga (26.0%) and Jaú (15.6%). This result confirmed the F test results for progeny differences and characterized Pindorama as a more suitable environment for expression of the genetic variability in this population. These results also agreed with those reported by Moreti et al. (1994) for the same trait.
The RP heritability coefficients associated with the different genetic effects used in the selection methods are shown in Table II. The heritability estimates obtained by the different models varied within and among locations according to the selection method used. Higher heritability values were observed for effects where the rubber tree was considered as a cross pollinating species, with greater values for Pindorama, followed by Votuporanga and Jaú.
The estimates obtained for the species, when considered as cross pollinating, compared to those found in models used for a mixed reproductive system, showed that heritability at the progeny level was practically unaffected at the three locations studied, even after allowing for the presumable inbreeding rate for the population. On the other hand, heritability at the individual level was considerably affected when progenies from open pollination were considered as half sibs.
When the rate of self pollination was not considered, the overestimation of heritability between the cross pollination and mixed models was 2% for Jaú, 4.6% for Votuporanga and 11.8% for Pindorama for the complete model. With the additive model, this variation was even more expressive: Pindorama, 18.7%, Votuporanga 7.4% and Jaú 3.2%.
These results agree with those reported by Resende et al. (1995b) for various Eucalyptus populations, for which the genetic gain (directly proportional to heritability) was overestimated during mass selection. More specifically for heritability, Hodge et al. (1996) pointed out that estimates for E. globulus and E. nitens progenies were overestimated mainly because of the effects of inbreeding depression which were disregarded when open pollination progenies were considered as half sibs.
For among-progeny selection, using open pollination and half sibs, the covariance (COVus,pm) between a selection unit and the breeding population was exactly the same as the genetic variance among progenies (Resende et al., 1995a). Consequently, there was no error in among-progeny selection and the heritability obtained could be used in expressing the genetic gain when working with legitimate half sibs. On the other hand, for mass selection among-half sib progeny, the among-progeny variance component was multiplied by four, increasing the covariance among the individuals in the progeny. Thus, use of the relationship s2A = 4 COVp caused overestimation of s2A (Resende et al., 1995b). This overestimation will be bigger the greater the self pollination rate.
Table III shows the accuracy and direct genetic gains associated with the different effects used in the selection methods for RP, assuming the species was cross pollinating with a mixed reproductive system.
The accuracy and genetic gain estimates for RP varied within and among locations in the different selection methods. When the accuracy values associated to the genetic gain are greater, the expected progress with selection was also greater, i.e., the greater the precision in selection the greater the gain. The genetic gain was much more expressive at Pindorama than at Votuporanga or Jaú. These results agree with those obtained by Moreti et al. (1994) for mass selection and can be explained by the high heritability values at the individual level at Pindorama compared to those at Votuporanga and Jaú. They also indicate that Pindorama was a more favorable environment for the expression of genetic variability, as shown by the RP coefficients of genetic variation (CVg%).
The multi-effect index approach was more advantageous than individual or combined selection because the gain estimates were always superior. This tendency was similar to that reported by Sturion et al. (1994), Resende et al. (1995a, 1996), and Sampaio (1996).
Resende and Higa (1994) discussed the tendency for higher gains in selection using the multi-effect index and explained that selection among and within progenies and combined selection used two sources of information for selection: the deviation of the individual value relative to the progeny mean in the block and the progeny mean relative to the general mean of the progeny test. These authors noted that in breeding schemes where the remaining seeds were not used, the additive genetic variance fraction was not considered, but was retained in the plot effects. The multi-effect index, in addition to using these two sources of information, further considers the plot effect and adds to the estimated gain those fractions of additive genetic variance retained in the plots.
Combined selection tends to select many individuals from certain families because of the greater weight given to the progeny information. In breeding populations, this does not present major problems, since in the next generation there will be selection against inbred individuals with undesirable traits, as long as the effective population size is adequate for obtaining the selective limit. Special care should be taken in production populations to prevent crossing among related individuals, which can lead to inbreeding depression. These precautions include careful orchard installation with a good distance among relations (Resende and Higa, 1994).
Higher accuracy and gains were observed for selection methods where the rubber tree was considered a cross pollinating species, with more expressive values at Pindorama, followed by Votuporanga and Jaú.
The overestimation of genetic gains in individual selection was 19.4% at Pindorama and Votuporanga and 19.5% at Jaú. With combined selection it was 17.6% at Pindorama, 16.1% at Votuporanga and 12.4% at Jaú. For multi-effect index selection, the rate was 18.2% at Pindorama, 16.6% at Votuporanga and 12.9% at Jaú.
More expressive values of the overestimation of genetic gains were obtained in the cross pollinating and mixed-additive models. For individual selection the overestimation was 30.5% at Pindorama and at Votuporanga and 29.9% at Jaú. For combined selection, it was 27.0% at Pindorama, 24.8% at Votuporanga and 18.8% at Jaú. For selection by the multi-effect index, it was 27.9% at Pindorama, 25.8% at Votuporanga and 20.2% at Jaú.
These results agree with those reported by Resende et al. (1995b) for several Eucalyptus species where the genetic gain was overestimated in individual selection. Overestimation was caused mainly when inbreeding depression was not considered and the open pollination progeny was treated as half sibs. In this context, the discussion by Resende et al. (1995b) about heritability is fully applicable when dealing with genetic progression and selection.
Our findings are similar to these of Moran and Bell (1983) and Griffin et al. (1987) for Eucalyptus species, which led to these species being considered as having a mixed reproductive system. The model suitable for populations with a mixed reproductive system has not been applied to the rubber tree.
The specific model for species with mixed reproductive systems presented by Cockerham and Weir (1984) allows better characterization of genetic structure of such populations. This practice provides a more suitable definition of the components of genetic variation and consequently of the effects of self pollination when estimating genetic parameters (Resende et al., 1995b). This approach should be useful for obtaining precise estimates of genetic parameters in rubber trees.
ACKNOWLEDGMENTS
R.B.C. is the recipient of a CAPES fellowship. Publication supported by FAPESP.
RESUMO
O presente trabalho objetivou comparar os componentes da variação genética e ganho genético obtidos através da seleção individual, combinada e pelo índice multi-efeitos em progênies de seringueira [Hevea brasiliensis (Willd ex Adr. de Juss.) Müell. Arg.], considerando-a como espécie alógama e de sistema reprodutivo misto, com taxa de aufecundação de 22%. Vinte e duas progênies de meio-irmãos foram plantadas nas Estações Experimentais de Pindorama, Votuporanga e Jaú, no estado de São Paulo, no delineamento de blocos ao acaso, com cinco repetições e dez plantas por parcela. Aos três anos de idade o caráter produção de borracha seca foi avaliado. Os resultados demonstraram haver variabilidade genética nas populações, bem como caracterizaram Pindorama como um ambiente mais propício para a expressão da referida variabilidade. As herdabilidades ao nível de indivíduos são consideravelmente afetadas ao assumir progênies de polinização aberta como sendo de meio-irmãos. Superestimativas consideráveis de ganhos genéticos ocorrem na seleção individual, combinada e índice multi-efeitos, quando não se considera o sistema reprodutivo misto para a seringueira. A seleção com base no índice multi-efeitos maximiza o progresso genético e deve ser utilizada.
APPENDIX
Derivation of the multi-effect index and associated accuracy.
The linear model for an individual observation in a progeny test is: Yijk = u + bj + pi + eij + dijk, where:
In terms of deviations the model is of the form:
The covariances between the components of the model with the additive genetic value are (Resende, 1991; Resende and Higa, 1994):
 , where:
, where:
r = additive genetic correlation between individuals within family: r = (1/4) for half-sibs and r = (1/2) for full-sibs;
COV(MF) = parent-offspring covariance;
COV(MTS or TS) = half-uncle-nephew (for half-sib families) or uncle-nephew (for full-sib families) covariances.
The covariances between the effects and the additive genetic effects are:
a) Within plot effect
b) Progeny effect
c) Plot effect
d) Block effect
The block effects can be neglected as a function of its low covariance with the genetic value. The variances of the relevant effects are:
a) Within plot effect
b) Progeny effect
c) Plot effect
The optimal selection procedure (the one that maximizes the correlation between predictand and predictor) is given by the multi-effect index (Resende and Higa, 1994):
The bi coefficients are given by:
Resolving these equations, the multi-effect index coefficients are:
= "heritability" of the within plot effect;
= "heritability" of the progeny effect;
= "heritability" of the plot effect;
The multi-effect index can be alternatively expressed as:

For the balanced case, the multi-effect index is equivalent to individual (animal model) BLUP, as demonstrated by Resende and Fernandes (1999).
The accuracy of the index is given by
This is equivalent to:
REFERENCES
(Received July 6, 1999)
- Alika, J.E. (1985). Heritability and genotypic gain from selection rubber (Hevea brasiliensis). Silvae Genet. 34: 1-4.
- Alika, J.E. and Onokpise, O.U. (1982). Estimation of heritability parameter for yield, girth and bark thickness in rubber (Hevea brasiliensis) from a single pair mating (S.P.M.) design. J. Plant. Crops 10: 102-108.
- Alves, M.R., Bandel, G. and Vencovsky, R. (1987). Avaliaçăo de seleçăo em seringueira (Hevea spp.) Bol. Fac. Cięnc. Agrar. Pará 16: 53-63.
- Boock, M.V., Gonçalves, P. de S., Bortoletto, N. and Martins, A.L.M. (1995). Herdabilidade, variabilidade genética e ganhos genéticos para produçăo e caracteres morfológicos em progęnies jovens de seringueira. Pesqui. Agropecu. Bras. 30: 673-681.
- Cockerham, C.C. and Weir, B.S. (1984). Covariances of relatives stemming from a population undergoing mixed self and radom mating. Biometrics 40: 157-164.
- Gonçalves, P. de S., Cardoso, M. and Bortoletto, N. (1988). Reduçăo do ciclo de melhoramento e seleçăo na obtençăo de cultivares de seringueira (Hevea spp.). Agronômico 40: 112-130.
- Gonçalves, P. de S., Cardoso, M., Colombo, C.A., Ortolani, A.A., Martins, A.L.M. and Santos, I.C.I. (1990). Variabilidade genética da produçăo anual da seringueira: estimativas de parâmetros genéticos e estudo de interaçăo genótipo x ambiente. Bragantia 49: 305-320.
- Gonçalves, P. de S., Martins, A.L.M., Gorgulho, E.P., Bortoletto, N., Cardoso, M. and Bermond, G. (1992). Variaçăo genética dos componentes do crescimento em progęnies jovens de uma populaçăo de clones de Hevea Bragantia 51: 161-171.
- Gonçalves, P. de S., Martins, A.L.M., Bortoletto, N. and Tanzini, M.R. (1996). Estimates of genetics parameters and correlations of juvenile characters based on open pollinated progenies of Hevea Braz. J. Genet. 19: 105-111.
- Griffin, A.R., Moran, G.F. and Fripp, Y. (1987). Preferential outcrossing in Eucalyptus regnans Aust. J. Bot. 35: 465-475.
- Henderson, C.R. (1963). Selection index and expected genetic advance. In: Statistical Genetics and Plant Breeding (Hanson, W.D. and Robinson, A.F., eds.). Publication 982: NAS-NRC, Washington, pp. 141-163.
- Hodge, G.R., Volker, P.W., Potts, B.M. and Owen, J.V. (1996). Comparison of genetic information from open-pollinated and control-pollinated progeny tests in two eucalyptus species. Theor. Appl. Genet. 92: 53-63.
- Lepsch, I.F. and Valadares, J.M.A. (1976). Levantamento pedológico detalhado da Estaçăo Experimental de Pindorama, SP. Bragantia 35: 13-40.
- Moran, G.F. and Bell, C. (1983). Eucalyptus In: Isozymes in Plant Genetics and Breeding (Tankley, S.D. and Orion, T.Y., eds.). Part B. Elsevier, Amsterdan, pp. 423-441.
- Moreti, D., Gonçalves, P. de S., Gorgulho, E.P., Martins, A.L.M. and Bortoletto, N. (1994). Estimativas de parâmetros genéticos e ganhos esperados com a seleçăo de caracteres juvenis em progęnies de seringueira. Pesqui. Agropecu. Bras. 29: 1099-1109.
- Namkoong, G. (1966). Inbreeding effects on estimation of genetic additive variance. For. Sci. 12: 8-13.
- Namkoong, G. (1981). Introduction to Quantitative Genetics in Forestry Castle House Publications, London.
- Nga, B.H. and Subramanian, S. (1974). Variation in Hevea brasiliensis I. Yield and girth data of the 1937 hand pollinated seedlings. J. Rubber Res. Inst. Malays 24: 69-74.
- Paiva, J.R. (1992). Variabilidade enzimática em populaçőes naturais de seringueira. Doctoral thesis, ESALQ-USP, Piracicaba, Săo Paulo.
- Paiva, J.R., Miranda Filho, J.B., Siqueira, E.R. and Valois, A.C.C. (1982). Prediçăo do ganho de alguns caracteres em seringueira em tręs esquemas de seleçăo. Pesqui. Agropecu. Bras. 17: 1646-1653.
- Paiva, J.R., Gonçalves, P. de S. and Valois, A.C.C. (1983). Avaliaçăo preliminar do comportamento de novos clones de seringueira em Manaus. Pesqui. Agropecu. Bras.18: 147-158.
- Resende, M.D.V. (1991). Correçőes nas expressőes do progresso genético com seleçăo em funçăo da amostragem finita dentro de famílias e populaçőes e implicaçőes no melhoramento florestal. Bol. Pesqui. Florestal 22/23: 61-77.
- Resende, M.D.V. de and Fernandes, J.S.C. (1999). Procedimento BLUP individual para delineamentos experimentais aplicados ao melhoramento florestal. Rev. Matemát. Estat. 17: 89-107.
- Resende, M.D.V. and Higa, A.R. (1994). Maximizaçăo da eficięncia da seleçăo em testes de progęnies de Eucalyptus através da utilizaçăo de todos os efeitos do modelo matemático. Bol. Pesqui. Florestal. 28/29: 37-56.
- Resende, M.D.V., Oliveira, E.B., Melinski, L.C., Goulart Junior, F.S. and Oaida, G.R.P. (1994). Seleçăo Genética Computadorizada - Selegen "Best Prediction". Manual do Usuário EMBRAPA - CNPF, Colombo.
- Resende, M.D.V., Araujo, A.J., Sampaio, P.T.B. and Wiecheteck, A.S. (1995a). Acurácia seletiva, intervalos de confiança e variância de ganhos genéticos associados a 22 métodos de seleçăo em Pinus caribaea var. hondurensis Rev. Floresta 24: 35-45.
- Resende, M.D.V., Vencovsky, R. and Fernandes, J.S.C. (1995b). Selection and genetic gains in populations of Eucalyptus with a mixed mating system. In: Proceedings of the Eucalypt Plantations Conference, Hobart, Australia, pp. 191-193.
- Resende, M.D.V., Moraes, M.L.T. and Paiva (1996). Comparaçăo de métodos de avaliaçăo genética e seleçăo no melhoramento da seringueira [Hevea brasiliensis (Willd. ex Adr. de Juss.) Müell. Arg.]. Floresta 26: 27-48.
- Sampaio, P.T.B. (1996). Variaçăo genética entre procedęncias e progęnies de Pinus oocarpa Schiede, Pinus caribaea var. hondurensis Barr. & Golf. e Pinus maximinoi, H.E. Moore e métodos de seleçăo para melhoramento genético. Doctoral thesis, UFPR, Curitiba, PR.
- Simmonds, N.W. (1989). Rubber breeding. In: Rubber (Webster, C.C. and Baulkwill, W.J., eds.). Longman, London, pp. 85-124.
- Siqueira, G.R. (1978). Estimativas de parâmetros genéticos de seringueira (Hevea spp.) em condiçőes de viveiro. Master´s thesis, UFV, Viçosa, MG.
- Squilace, A.E. (1974). Average genetic correlations among offspring from open pollinated forest trees. Silvae Genet. 23: 149-156.
- Sturion, J.A., Resende, M.D.V., Carpanezzi, A.A. and Zanon, A. (1994). Variaçăo genética e seleçăo para características de crescimento em teste de progęnies de Mimosa scabrella var. aspericarpa Bol. Pesqui. Florestal 28/29: 73-83.
- Tan, H. (1977). Estimates of general combining ability in Hevea breeding at the Rubber Research Institute of Malaysia. I. Phases II and III a. Theor. Appl. Genet. 50: 29-34.
- Tan, H. (1978a). Assessment of parental performance for yield in Hevea breeding. Euphytica 27: 521-512.
- Tan, H. (1978b). Estimates of parental combining abilities in rubber (Hevea brasiliensis) based on young seedlings progeny. Euphytica 27: 817-823.
- Tan, H. and Subramanian, S. (1976). A five-parent diallel cross analysis for certain characters of young Hevea seedlings. In: Proceedings of International Rubber Conference, 1975, RRIM, Kuala Lumpur, pp. 13-16.
- Tan, H., Mukherjee, T.K. and Subramanian, S. (1975). Estimates of genetic parameters of certain characters in Hevea brasiliensis Theor. Appl. Genet. 46: 181-190.
- Valois, A.C.C., Pinheiro, E., Conceiçăo, H.E.O. and Silva, M.N.C. (1978). Competiçăo de porta-enxertos de seringueira e estimativas de parâmetros genéticos. Pesqui. Agropecu. Bras 13: 49-59.
- Vencovsky, R. (1987). Herança quantitativa. In: Melhoramento e Produçăo do Milho (Paterniani, E. and Viegas, G.P., eds.). 2nd edn. Fundaçăo Cargill, Campinas, pp. 137-214.
Publication Dates
-
Publication in this collection
04 May 2001 -
Date of issue
Sept 2000
History
-
Received
06 July 1999