Changes in G+C content of a neutrally evolving gene under a non-reversible dynamics measured by computer simulations based on experimental evolution data

BIOINFORMATICS

RESEARCH ARTICLE

Changes in G+C content of a neutrally evolving gene under a non-reversible dynamics measured by computer simulations based on experimental evolution data

Adriana Brunstein^I; Leonardo Varuzza^II; Gerdine F. O. Sanson^I; Marcelo R. S. Briones^I

^IUniversidade Federal de São Paulo, Escola Paulista de Medicina, Departamento de Microbiologia, Imunologia e Parasitologia, São Paulo, SP, Brazil

^IIUniversidade de São Paulo, Instituto de Matemática e Estatística, Departamento de Ciência da Computação, São Paulo, SP, Brazil

^{Correspondence}

ABSTRACT

To evaluate the effects of non-reversibility on compositional base changes and the distribution of branch lengths along a phylogeny, we extended, by means of computer simulations, our previous sequential PCR in vitro evolution experiment. In that study a 18S rRNA gene evolved neutrally for 280 generations and a homogeneous non-stationary model of base substitution based on a non-reversible dynamics was built from the in vitro evolution data to describe the observed pattern of nucleotide substitutions. Here, the process was extended to 840 generations without selection, using the model parameters calculated from the in vitro evolution experiment. We observed that under a non-reversible model the G+C content of the sequences significantly increases when compared to simulations with a reversible model. The values of mean and variance of the branch lengths are reduced under a non-reversible dynamics although they follow a Poisson distribution. We conclude that the major implication of non-reversibility is the overall decrease of branch lengths, although no transition from a stochastic to an ordered process is observed. According to our model the result of this neutral process will be the increase in the G+C content of the descendant sequences with an overall decrease in the frequency of substitutions.

Key words: molecular evolution; experimental phylogenetics; neutral theory; mathematical models of nucleotide substitutions

Introduction

The evolutionary process can be viewed as a consequence of mutations, chance and selection acting on a given population, leading to changes in the genetic scenario. Evolutionary history can be represented using phylogenies inferred from aligned sequence data. The maximum likelihood approach (Felsenstein, 1981) requires explicit probabilistic models of nucleotide substitution. The most commonly used models vary from the simple Jukes and Cantor model (Jukes and Cantor, 1969), to the most general one, the general time reversible model (Rodríguez et al., 1990). Although these models are approximations of the real process and describe satisfactorily most of them, they all assume reversibility of the substitutions probability matrix, and so are based on an evolutionary process that is independent of time direction.

An immediate consequence of assuming reversibility is the impossibility of defining, a priori, a root for the phylogenetic tree, in other words, the impossibility of establishing a defined ancestor-descendant relation of the character states. Therefore, any proposition concerning the evolutionary direction can be done only if some information extrinsic to the process is supplied, such as outgroups and fossil records. Use of reversible models, with its equivalence of ancestor and descendant states, leads to a lack of relevant information about the evolutionary mechanism which may even contribute to an erroneous estimation of branch lengths of the phylogenetic tree. The advantage of assuming the reversibility of the substitution process is the mathematical and computational simplification in phylogenetic inference, because the pulley principle allows any segment of the unrooted tree to be treated as containing the root (Felsenstein, 1981).

At the chemical level, the substitution process from one given base to another cannot be considered as reversible. For example, in the experimental phylogeny of a bacteriophage, the accelerated rate of change was induced by the presence of a mutagenic agent which changed the tempo and the mode of evolution, because the mutagenic agent probably biased substitutions from G to A and C to T (Bull et al., 1993). Therefore, the nucleotide substitution dynamics would be better described with non-reversible models. Although models based on non-reversible probability matrices have been proposed (Yang and Roberts, 1995; Galtier and Guoy, 1998; Schadt et al., 1998; Galtier et al., 1999), the long term effects of non-reversibility in neutral evolution remains to be tested.

Here we want to study the consequences of assuming non-reversibility of the substitutions probability matrix in a neutrally evolving process. Neutral substitutions are very interesting for phylogenetic purposes and provide a useful tool in order to study the role of the process dynamics. Under neutral theory substitutions conform to a Poisson process, so that the index of dispersion R, the ratio of the variance to the mean, is expected to equal one (Kimura, 1983).

Material and Methods

Tests of homogeneity and neutrality of the in vitro evolution PCR process

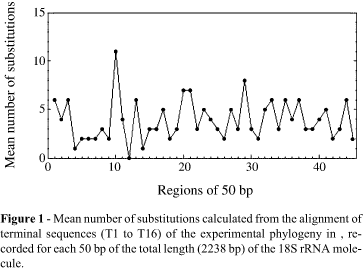
The substitution process along the real phylogeny of the evolutionary process obtained from the PCR evolution method (Sanson et al., 2002) was studied by verifying whether the nucleotide substitutions were homogeneous along the four steps of amplification and cloning by means of comparing the observed substitutions in each step. The proportions of the different types of substitutions were scored and tested for a homogeneity hypothesis, using the Freeman-Halton test. The spatial homogeneity was checked, to test if the substitutions in the terminal sequences were uniformly distributed along the 18S rRNA molecule. For this, the molecule was divided into 45 regions of 50 nucleotides each and the mean number of substitutions per region was recorded. Then the number of substitutions in each 50 nucleotides segment was compared to a descriptive analysis using the chi-square test. The descriptive analysis represents the mean number of substitutions of the 45 segments. All statistical tests were performed with SPSS program (SPSS inc.)

Computer simulations

The real evolutionary process described above was reproduced and extended by means of computer simulation in order to study its long-time behavior. A computer program for this purpose was developed in C language and is available upon request. The parameters of this simulation were obtained from the experimental phylogeny generated and the associated model in our previous work (Sanson et al., 2002). The real phylogeny obtained consisted of 15 dichotomies from the ancestor (a known SSU rRNA gene sequence, 2238 bp) to 16 terminal sequences (Figure 1 of Sanson et al., 2002). As described in that work the instantaneous rate matrix (Q-matrix) was built from the observed number of changes in each of the 16 terminal categories. The Q-matrix was written as in Table 1 of Sanson et al., 2002, number in parenthesis. The substitution probability matrix (P-matrix) was calculated from the relation (Swofford et al., 1996) and characterizes a stochastic Markov model with non-reversible dynamics that describes the action of the Taq DNA polymerase. The P-matrix elements P_ij(t) (i,j = A,C,G,T) are described in Table 3 of (Sanson et al., 2002).

Results

The in vitro evolution by PCR simulates neutral evolution

First, to verify whether the real phylogeny generated by PCR evolution (Sanson et al., 2002) reflects neutral evolution we determined whether the phylogeny branch lengths fitted a Poisson distribution. The real phylogeny has a total of 30 branches with absolute lengths from 1 to 13 substitutions (Figure 2A of Sanson et al., 2002). The distribution of these branches is Poisson-like with a mean of 5.37, variance of 7.3, and an index of dispersion R of 1.36, as confirmed by a performed chi-square goodness-of-fit test that returned a c² value of 8.4 for 13 degrees of freedom at a descriptive level (p-value) of 0.82. This means that the PCR evolution, as performed, reflects neutrality. In addition, we studied the proportions of different types of substitutions along the phylogeny (table 1). Due to the large number of observed events with null frequency, the Freeman-Halton exact test was applied. The test shows that the distribution along time is homogeneous (c² = 36.8126 for 30 degrees of freedom, p-value = 0.167).

The neutrality was also tested to verify whether the substitutions occurred randomly along the sequence length. Figure 1 shows that the mean number of substitutions observed for each 50 bp region along the entire molecule (2238 bp) occur at random, in other words, there are no "hot spots" for substitutions. This observation is supported by the descriptive analysis of the substitutions along the sequence, shown in Table 2, which characterizes a Gaussian distribution.

Computer simulation of evolution using experimental evolution data

Because the PCR evolution data reflect neutral evolution we extended the process, by means of computer simulations, to verify the effect of a non-reversible dynamics on a neutral process. Specifically we addressed whether: (1) DNA sequences could increase the G+C content neutrally and (2) the process would depart from neutrality, e.g., by changing from a Poisson distributed process to an ordered process in the absence of selection. For this we made a computer program in which the dynamics that evolve a sequence down a branch of the tree is given by the probability matrix P(t), where each element P_ij(t) describes the probability of a given site of the sequence which is in state i to be in state j after a time course t. For each site of a sequence which is in state i, a uniformly distributed random number between 0 and 1 is sorted and compared to the row of the P-matrix corresponding to state i, in order that one of the possible outcome states j can be chosen. All sites are then simultaneously updated. This procedure is repeated twice for each ancestor considered, generating two descendants in a way that the same bifurcated structure of the original topology is maintained.

Although an evolutionary process is better represented with sequential updating, the alternative procedure chosen here was adopted since the main interest of this work is the study of the behavior of the branch lengths distribution, and not the substitution process by itself. In this way, we wanted to define a model-based Markov chain with Monte Carlo dynamics that was able to output the value of the branch length connecting an ancestor to a descendant and separated in time by a t amount. So, t is the only parameter left to be determined for each model and actually it is responsible for a given observed configuration of branch lengths.

Because we had a real phylogeny, the parameter t was iterated on simulations of analogous topologies (starting with the real ancestor) until the mean value of the branch lengths distribution achieved a value close to that really observed. We calculated t for the Jukes and Cantor model that represents the simplest one with reversible dynamics, and for the built non-reversible model. The process was extended until generation 840, with each generation a PCR cycle. The resulting phylogeny has 4096 terminal sequences and a total of 8190 branches. Four types of ancestors were also used: the real one, with G+C content of 50%, and four random ones generated (2238 bp each) with predetermined G+C content of 55%, 65%, 75% and 100%. For each ancestor and model 100 sets of simulations were performed.

The calculated values of t used in the probability matrix are 1/310 for the Jukes and Cantor model and 1/105 for the non-reversible model. In both cases we have obtained for the mean branch length the value 5.4 ± 2.3. In Figure 2 we see the distribution of branch lengths of the simulated generation 840 evolved by the Jukes and Cantor model (full line) and the non-reversible model (dotted line) for the four types of ancestors: (a) real ancestor with 50% G+C content, (b) ancestor with 55% G+C content, (c) ancestor with 65% G+C, (d) ancestor with 75% G+C content and (e) ancestor with 100% G+C content. The histogram frequencies are averaged over the 100 sets of simulations and normalized to the total number of branch lengths. The mean and variance of these distributions are in Table 3.

Discussion

In our previous work (Sanson et al., 2002) a known phylogeny was generated and a non-reversible substitution model based on neutrally evolving DNA sequences was built. In the present work the neutrality hypothesis of this experimental process was validated testing temporal and spatial behavior of the substitution process with appropriate statistical tests. The results show that all observed fluctuations are within the expected range of a neutrally evolving process.

As pointed out elsewhere , compositional changes are a major feature of genome evolution. Usually homogeneity (constancy of the rate matrix) and stationarity (constancy of base composition over the tree) hypotheses are assumed. The authors argue that if these assumptions were true, equal nucleotide frequencies would be expected in present-day sequences.

The non-reversible model described here can be defined as homogeneous, once the rate matrix is constant over time. But due to non-reversibility the base composition over the whole tree departures from constancy, violating the stationarity hypothesis. The dynamics by itself deals with compositional base changes. The process implicitly associates, through the definition of Monte Carlo intervals, different rates of substitution to each nucleotide which occupies a site of the sequence considered.

As we saw by raising the G+C content of the ancestor, the process evolved by means of the Jukes and Cantor model does not change its mode of evolution. Equal nucleotide frequencies are observed along the tree even at extended generations and different contents of G+C of the ancestor. The distribution of branch lengths maintains the same mean and variance observed in the real phylogeny.

In the case of the non-reversible model, the mean length of the branches decreases with raising G+C content of the ancestor. This is observed even when simulations of the original topology (with 30 branches) are performed (results not shown). At a glance we could expect, due to the accumulation of G and C, the loss of stochasticity of the distribution of branch lengths as long as new generations are included in the process. This is not true. The distribution continues to be stochastic with the index of dispersion keeping its constancy as expected under the neutral theory (Poisson distribution, R ~1), and as confirmed by the simulated generation 840. The neutrality of the process is not affected by the non-reversibility.

Concerning the violation of stationarity, we note that even in the process which evolved from the real ancestor, intermediate or final states with more than 55% of G+C content are formed. These can lead to local regions having different branch lengths distributions than that globally expected under the assumption of a reversible model. A non-reversible model can deal with base composition biases and makes it possible to recover information more accurately about past base content and changes.

The non-reversible models have major implications when used to simulate evolutionary processes. At least in the scope of our study, we observed an overall decrease of branch lengths in phylogenies. Also, this decrease was not followed by a transition from a stochastic to an ordered process, and therefore, departure from neutrality might be only a consequence of selection. Our simulations were based on data reflecting the evolution of a DNA segment replicated by Taq DNA polymerase, and therefore, we do not exclude that the Taq DNA polymerase itself, with its associated mutational bias, is a product of selection. Nevertheless, our computer simulations show that, provided a non-reversible dynamics underlies the process, it is possible to increase the G+C content and decrease the overall frequency of substitutions in descendant sequences in the absence of selection, which then reflects the equilibrium state reached by the system.

Acknowledgments

We would like to thank J. F. Perez, Scientific Director of Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for sequencing equipment and computer facilities made available to us through the ONSA Brazilian sequencing network. G.F.O.S received a graduate fellowship from CNPq (Brazil) and L.V. was supported by FAPESP, Brazil. This work was supported by grants to A.B. from FAPESP, Brazil and M.R.S.B from FAPESP and CNPq (Brazil) and the International Research Scholars Program of the Howard Hughes Medical Institute (USA).

Galtier N, Tourasse NJ and Guoy M (1999) A nonhiperthermophilic common ancestor to extant life forms. Science 283.

Kimura M (1983) The Neutral Theory of Molecular Evolution. Cambridge Univ. Press, Cambridge.

Received: August 15, 2003; Accepted: August 20, 2004

• Bull J, Cunningham CW, Molineux I, Badgett M and Hillis DM (1993) Experimental molecular evolution of bacteriophage-T7. Evolution 47:993-1007.
• Felsenstein J (1981) Evolutionary trees from DNA sequences: A maximum likelihood approach. Journal of Molecular Evolution 17:368-376.
• Galtier N and Guoy M (1998) Inferring patterns and process: Maximum likelihood implementation of a nonhomogeneous model of DNA sequence evolution. Molecular Biology and Evolution 15:871-879.
• Jukes T and Cantor C (1969) Evolution of protein molecules. In: Munro H (ed) Mammalian Protein Metabolism. Academic Press, New York, pp 21-132.
• Rodríguez F, Oliver J, Marín A and Medina J (1990) The general stochastic model of nucleotide substitution. Journal of Theoretical Biology 142:485-501.
• Sanson G, Kawashita S, Brunstein A and Briones M (2002) Experimental phylogeny of neutrally evolving DNA sequences generated by a bifurcate series of nested polymerase chain reaction. Molecular Biology and Evolution 19:170-178.
• Schadt E, Sinsheimer J and Lange K (1998) Computational advances in maximum likelihood methods for molecular phylogeny. Genome Research 8:222-233.
• Swofford DL, Olsen GJ, Waddel PJ and Hillis DM (1996) Phylogenetic inference. In: Hillis DM, Moritz C and Mable BK (eds) Molecular Systematics. Sinauer Associates, Sunderland, MA, pp 407-514.
• Yang Z and Roberts D (1995) On the use of nucleic acid sequences to infer early branchings in the tree of life. Molecular Biology and Evolution 12:451-458.

Publication Dates

• Publication in this collection
  14 Jan 2005
• Date of issue
  2004

History

• Accepted
  20 Aug 2004
• Received
  15 Aug 2003