Suspensory Tethers and Critical Point Membrane Displacement in Endolymphatic Hydrops

Abstract

Introduction

Grossly displaced membranes are characteristic of endolymphatic hydrops. The process whereby physiological membrane displacement becomes pathological may be mediated by stress, but the membrane biomechanics underlying this transition are unclear.

Objective

This study seeks to determine the role of suspensory tethers during pressure-induced membrane displacement in the generation of the membranous lesions seen in this disease entity using a biomechanical model approach.

Methods

The location of membrane suspensory tethers was identified histologically. The influence of tethers on model membrane configuration during displacement was assessed graphically. The relationship of membrane configuration during displacement to curvature radius was quantified trigonometrically. The relationship of curvature radius to stress susceptibility was determined mathematically. The net effect of suspensory tethers on membrane stress levels for various degrees of membrane distention and displacement was then calculated numerically.

Results

In the inferior labyrinth, suspensory tethers are found to occur on the membranes’ boundaries. Such tethering is found to impose a biphasic effect on membrane curvature with increasing degrees of displacement. As a consequence, tensile stress susceptibility is found to decline with initial membrane displacement to a critical point nadir beyond which stress then increases monotonically. No such effect was found for the superior labyrinth.

Conclusion

Boundary tethers in the inferior labyrinth are associated with significant tensile stress reductions until a critical point of membrane displacement is reached. Displacements short of the critical pointmay be physiological and even reversible,whereas such displacements beyond the critical point are apt to be overtly hydropic and irreversible.

Keywords:
endolymphatic hydrops; membranes; rupture

Introduction

Grossly displaced membranes are characteristic of endolymphatic hydrops.¹ The process whereby physiological membrane displacement becomes pathological may be mediated by stress, but the membrane biomechanics underlying this transition are unclear. Previous work in this area has found that membrane stress is dependent on labyrinth chamber configuration.² Membrane tethers have the potential to affect chamber configuration in response to transmural pressure, and thus influence membrane displacement and associated stress. This study examines a model membrane fixed along its margins to gain insight into the impact of suspensory tethers on displacement and stress in the membranous labyrinth and their possible role in the generation of endolymphatic hydrops.

Methods

A biomechanical model was utilized to determine how tethers control membrane displacement and stress levels in the presence of raised transmural pressure. The position of suspensory membrane tethers in the labyrinth was identified based on established normal temporal bone histology. How these tethers might influence membrane configuration during displacement under pressure was assessed according to the location of the attachment points, and used to suggest a theoretical model for a membrane tethered along its margins. The relationship of membrane configuration to curvature radius was quantified by constructing a model diagram that reflected the anatomy, and then analyzing the components trigonometrically. The relationship of curvature radius to stress susceptibility was determined mathematically, using shell theory for the formulation. The net effect of suspensory tethers on membrane stress levels for various degrees of membrane displacement and distention was then calculated numerically.

Results

In the inferior labyrinth, the vestibular membranes are tethered along their edges only, with their surfaces free of suspensory elements. Reissner membrane is tethered along its medial boundary to the spiral limbus, and laterally to the otic capsule at the upper margin of the stria vascularis. The saccular membrane is tethered along its circumferential edge to the margins of the spherical recess. In contrast, suspensory tethering of the pars superior membranes³ is quite different, with tethers attached in a diffuse manner to the external surfaces of the utricle, ampullas, and canals. These features are shown in Fig. 1, in which tethers in the superior labyrinth are labeled as ‘trabecular mesh’, and saccular and Reissner membrane tethers are simply their attachment points along their edges to the bony labyrinth.

Fig. 1
A vertical temporal bone section showing diffuse trabecular mesh surface tethers suspending the chambers of the superior labyrinth. Reissner membrane and the saccule membrane are tethered only at their margins.

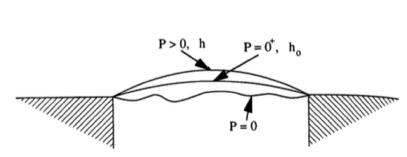
For the inferior labyrinth, the influence of tethers on membrane displacement under pressure was based on their attachment to the membrane boundaries. Boundary tethering of Reissner membrane along its parallel edges was judged to cause this membrane to bulge into the scala vestibuli and assume a partial cylindrical shape as it distends⁴ under pressure. Boundary tethering of the saccular membrane along its circumferential edge was judged to cause this membrane to bulge into the perilymphatic cistern of the vestibule and assume a partial spherical shape as it distends under pressure. These features are consistent with a model membrane that assumes a three dimensional (3-D) spherical or cylindrical shape, since both have circular cross sections. In both cases, these membranes are assumed to be initially lax when the transmural pressure ‘P’ is zero, as seen in Fig. 2. In the presence of a differential degree of pressure (P = 0⁺), the membrane will exhibit a smooth virtually unstressed and minimally displaced configuration tethered between its fixation points. Application of a discrete increment of pressure above zero will cause the membrane to undergo definite displacement (P > 0) in a smooth circular arc.

Fig. 2
The effect of transmural pressure P on membrane displacement.

Progressive degrees of membrane displacement in the model were found to impart a curvature change to the membrane that is biphasic, as shown in Fig. 3. The curvature initially increases as the membrane bulges out from its initial flat position with infinite curvature radius. The curvature becomes maximal when the membrane assumes a hemi-circular profile and its curvature radius is minimal. Further displacement results in an increasing curvature radius and progressive flattening of the membrane.

Fig. 3
Membrane displacements with differing degrees of curvature as bulging proceeds in membranes with boundary tethering.

In the inferior labyrinth, the model projects that maximum curvature occurs when Reissner membrane achieves a hemi-cylindrical configuration with a diameter equal to the normal width of the same membrane. In the saccule, this maximum occurs when a hemispherical shape is achieved, with a diameter equal to that of the spherical recess.

In contrast, in the superior labyrinth, surface tethers in the form of a trabecular mesh appear positioned to prevent chamber collapse rather than influence distention. As a consequence, the boundary-tethered model does not apply to the membranes of the superior labyrinth, and each chamber therein is projected to distend simply and uniformly with a monophasic progressive increase in curvature radius from its normal configuration.

The relationship between model membrane displacement and curvature radius for a boundary-tethered membrane was analyzed trigonometrically. Fig. 4 shows the structural geometry of the anatomy, and illustrates how the distended length of Reissner membrane is related to the curvature radius.

Fig. 4
Reissner membrane's RM distending to length S when membrane tension t is induced by transmural pressure P. R indicates the distended membrane's radius of curvature, while β is the angle that R makes with the centerline of the membrane.

Trigonometrically, the relationship between these variables was found to be a sine function, as shown in Eq. 1.

$\text{0}\text{.5 RM/R = Sine}\beta ,$ Eq. 1

where RM represents the length of Reissner membrane; R represents the curvature radius of the arc segment S; and β represents the angle that R makes with the membrane centerline.

Fig. 4 also illustrates that the membrane arc segment S is related to the curvature radius R and the angle β. This relationship is described in Eq. 2.

$\text{0}\text{.5S = R}\times \beta ,$ Eq. 2

where β is measured in radians and represents the contained angle in radians; S represents the length of the arc segment of displace membrane; and R represents the curvature radius of the arc segment S.

Substituting the value of β from Eq. 1 into Eq. 2 yields the analytical relationship between arc curvature radius R and arc length, S as shown in Eq. 3.

$\text{S = 2}\times \text{R}\times {\text{Sin}}^{\text{-1}}\text{(0}\text{.5RM/R)}$ Eq. 3

The effect of the membrane arc curvature radius on tensile stress susceptibility was evaluated using the relationship between membrane stress and transmural pressure in a thin shelled containment vessel,⁵ as shown in Eq. 4. Tensile stress is defined as the amount of tension in the membrane per unit of cross-sectional area.

$\text{t = p}\times \text{sf}\times \text{r/w}\text{,}$ Eq. 4

where t represents membrane tensile stress; p represents transmural pressure; sf represents membrane shape factor; r represents membrane radius of curvature; and w represents membrane wall thickness.

In this analysis, the shape factor is invariant for a given chamber (a cylindrical shape factor of 1.0 for Reissner membrane, the utricle and all three canals, and a spherical shape factor of 0.5 for the saccular membrane and all ampullae).² The stresses presented are engineering stresses that assume a constant wall thickness. For heuristic purposes, transmural pressure may be normalized to a value of unity. This leaves the radius of curvature as the main determinant of membrane stress in this analysis.

The resulting relationship between stress and membrane arc length in a boundary-tethered membrane was then calculated numerically and displayed graphically. With curvature radius ‘R’ as a marker for tensile stress, as noted before, Fig. 5 shows the net effect of boundary tethers on membrane stress for various degrees of membrane arc length. Boundary tethers can be seen to account for a precipitous decline in curvature radius and stress with increasing degrees of displacement from point A to point B. Curvature radius and stress eventually reach a critical minimum point at displacement point C. Thus, the critical point is defined as the point in which membrane stress stops decreasing and starts to increase as membrane displacement progresses. Beyond point C, gradual rises in curvature radius and stress are associated with marked degrees of displacement up to point D and beyond.

Fig. 5
Graph illustrating how curvature radius R, a marker for stress, varies with degree of membrane arc length S.

In the superior labyrinth, surface tethers cannot be expected to oppose membrane distention. As a consequence, there is no initial reduction in curvature radius, since there are no boundary tethers. Membrane curvature radius and attendant stress levels in the utricle, ampullae and canals can all be expected to simply increase monotonically. In Fig. 5 this would correspond to point D and beyond.

Discussion

The importance of membrane micromechanics in organ functioning is clear from an early study on the effect of surfactant in pulmonary alveolae.⁶ That work examined how alterations in alveolar fluid surface tension could influence membrane mechanical behavior in the lung. That work showed that a factor extrinsic to the membranes could indeed alter membrane mechanics.

This current work examines the influence of extrinsic suspensory tethers on membrane mechanical behavior in the membranous labyrinth of the ear. It needs to be emphasized that the model results are completely general, and apply to any thin membrane, regardless of composition and elastic strength. Thus, the effect of this tether action in producing a biphasic relationship between stress and displacement is not a property intrinsic to the membranes of the labyrinth. As a consequence, membrane elasticity does not enter into the calculations.

The graph of curvature radius ‘R’ versus the degree of membrane arc length ‘S’ is not the result of experimental data. Rather, it derives solely from the geometry imposed by the anatomy. It describes the necessary relationship between membrane arc length and the attendant membrane curvature radius for a membrane bulging between two fixed points. Any pressure-displaced membrane segment tethered at its edges and bulging must obey this geometric constraint.

These features lead to an unexpected and counterintuitive finding for boundary tethered membranes of the pars inferior. Namely, progressive degrees of pre-critical displacement are associated with lessening membrane tension, while further increases in membrane displacement beyond the critical point region are associated with rising membrane tension. This is because the tensile stress vector in the membrane opposing transmural pressure becomes less and less oblique as the critical point is approached. At the critical point, stress reaches its nadir when the membranes are tethered perpendicular to their bony anchor points and the membrane exhibits a hemi-circular profile with maximum curvature, as shown in Fig. 3. With displacements beyond the critical point, the membrane is tethered at an increasingly oblique angle to its anchorage, with an attendant increase curvature radius and stress.

Thus, the stress–displacement function for tethered membranes may act as a fail-safe mechanism, wherein limited membrane displacements in the pre-critical point zone are generally safe displacements, while greater displacements in the post-critical point zone will be at risk for membrane failure. In contrast, in the superior labyrinth, surface tethered membranes enjoy no such safety zone, as they displace and must instead rely on thick highly-curved membranes to keep stress and distention minimal from the outset.

These findings provide insight into membrane behavior in endolymphatic hydrops. In the inferior labyrinth, Reissner membrane and the saccular membrane are found to be relatively flat and boundary tethered in normal temporal bone specimens, as seen in Fig. 1. Low-amplitude physiological displacements are likely occurring within the elastic limits of these membranes, since no permanent distention of these membranes is seen over a lifetime in most individuals. Thus, it is logical to speculate that reversible elastic distentions are occurring in the pre-critical zone of membrane displacement.

When visible membrane displacement is encountered in a temporal bone specimen, it is usually designated as endolymphatic hydrops⁷. The earliest stages of hydrops occur in the pars inferior, and are limited to the cochlear apex. Most apical lesions demonstrate modest displacement at or near the critical point, as shown in Fig. 6. Displacements near the critical point can also be encountered in the saccule, as shown in Fig. 7. These low degrees of membrane displacement in the cochlea and saccule in early hydrops along with their smooth continuous contours suggest that the decreasing stress levels as the critical point is approached act to arrest and limit further membrane displacement.

Fig. 6
Near-critical point displacement of Reissner membrane.

Fig. 7
Near-critical point displacement of the saccular membrane with no apparent utricular distention.

The progression of hydrops appears to be orderly.⁸ The pars superior often shows minimal or no abnormality in the presence of pars inferior lesions. In this regard, it should be noted that the utricle in Fig. 7 appears little affected, suggesting that it is able to resist whatever pressure is displacing the saccular membrane.

Higher pressures are likely to displace the saccular membranes beyond the critical point into the zone of obvious membrane failure, as evidenced in Fig. 8. Here, the grossly displaced saccular membrane is irregular in contour and adherent to the stapes footplate. Such extreme distention and fibrous attachment to the bony labyrinth, as well as membrane ruptures when they occur, are clearly suggestive of irreversible pathology.

Fig. 8
Mild uniform distention of the utricular membranes in the presence of severe irreversible saccular hydrops.

As compared with Fig. 7, the utricle in Fig. 8 is dilated enough to open the endolymphatic valve; yet, it has a smooth contour, and maintains its regular shape. This suggests that its thicker membranes are keeping stress low and displacement limited. Visible elements of the trabecular mesh on the utricle surface appear not to impede its distention.

These findings suggest that initial displacements of the inferior labyrinth membranes can be limited to the subcritical point zone. The boundary-tethered Reissner and saccular membranes are able to undergo a mild subcritical displacement to achieve a more favorable configuration in which these membranes can better resist pressure while experiencing less stress. Membrane ruptures are virtually never seen with displacements in the subcritical zone.⁹ But with displacements beyond the critical point, these membranes are usually distorted and/or ruptured, clear evidence of irreversibility. In contrast, the surface-tethered utricle, ampullae and canals appear to be able to keep stresses low from the start due to an inherently better membrane mechanical advantage¹⁰ conferred by greater membrane thicknesses and higher curvatures that enable them to better resist distention.

Conclusion

In the membranes of the inferior labyrinth, the model projects that boundary tethers afford a limited degree of protection against hydropic distention. Such boundary tethers induce increasing curvature to Reissner's membrane and the saccular membrane, enabling them to better resist distention, at least up to a critical point. The effectiveness of this strategy is reflected in the fact that most temporal bones do not evince any hydropic change. Some of those that do exhibit mild displacement at or near the critical point may be benefitting from stress reduction. However, once the critical point distention has been exceeded, the stress reduction safety feature is lost, and overt endolymphatic hydrops with grossly distended and/or ruptured membranes is apt to ensue.

In the superior labyrinth, external surface tethering cannot provide the membranes with the protective stress reductions in the way that boundary tethers do. Rather, stress protection in the pars superior is conferred by other anatomic features: naturally high curvatures and thick membranes that keep stress levels and attendant distention inherently low. The effectiveness of this strategy is reflected in the fact that only a minority of cases of endolymphatic hydrops involve the pars superior.

References

• ¹
  Schuknecht HA.Pathologyof theEar.Cambridge:HarvardUniversity Press; 1974
• ²
  Pender DJ. A model analysis of static stress in the vestibular membranes. Theor Biol Med Model 2009;6:19
• ³
  Nomura Y. Morphological Aspects of Inner Ear Disease. Tokyo: Springer; 2014
• ⁴
  Pender DJ. A model design for the labyrinthine membranes in mammals. Laryngoscope 2014;124(06):E245-E249
• ⁵
  Pender DJ. Membrane stress proclivities in the Mammalian labyrinth. Int Arch Otorhinolaryngol 2014;18(04):398-402
• ⁶
  Avery ME, Mead J. Surface properties in relation to atelectasis and hyaline membrane disease. AMA J Dis Child 1959;97 (5, Part 1):517-523
• ⁷
  Schuknecht HF, Gulya AJ. Endolymphatic hydrops. An overviewand classification. Ann Otol Rhinol Laryngol Suppl 1983;106:1-20
• ⁸
  Pender DJ. Endolymphatic hydrops and Ménière's disease: a lesion meta-analysis. J Laryngol Otol 2014;128(10):859-865
• ⁹
  Antoli-Candela F. The Histopathology of Meniere's Disease. Acta Otolaryngol 1976;340:1-42
• ¹⁰
  Pender DJ. Membrane mechanical advantage and its role in endolymphatic hydrops. Otorinolaringologia 2016;66(03):93-98

Publication Dates

• Publication in this collection
  Jul-Sep 2018

History

• Received
  14 Jan 2017
• Accepted
  04 June 2017