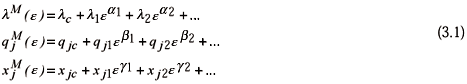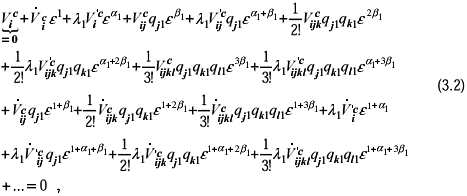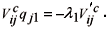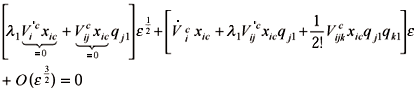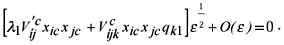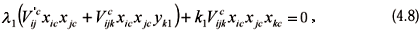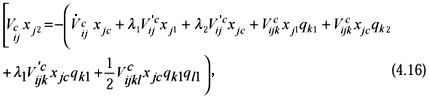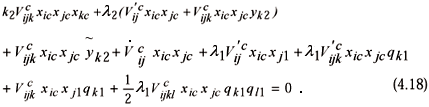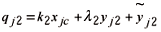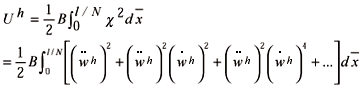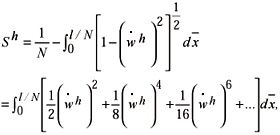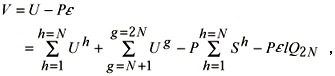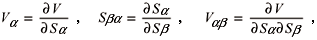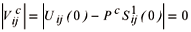A new approach to evaluate imperfection sensitivity in asymmetric bifurcation buckling analysis

Abstract

A direct procedure for the evaluation of imperfection sensitivity in bifurcation problems is presented. The problems arise in the context of the general theory of elastic stability for discrete structural systems, in which the energy criterion of stability of structures and the total potential energy formulation are employed. In cases of bifurcation buckling the sensitivity of the critical load with respect to an imperfection parameter e is singular at the state given by epsilon =0, so that, a regular perturbation expansion of the solution is not possible. In this work we describe a direct procedure to obtain the relations between the critical loads, the generalized coordinates at the critical state, the eigenvector, and the amplitude of the imperfection, using singular perturbation analysis. The expansions are assumed in terms of arbitrary powers of the imperfection parameter, so that both exponents and coefficients of the expansion are unknown. The solution of the series exponents is obtained by searching the least degenerate solution. The formulation is here applied to asymmetric bifurcations, for which explicit expressions of the coefficients are obtained. The use of the method is illustrated by a simple example, which allows consideration of the main features of the formulation.

Buckling; sensitivity analysis; imperfections; singular perturbations

A New Approach to Evaluate Imperfection Sensitivity in Asymmetric Bifurcation Buckling Analysis

Enrique G. Banchio

Luis A. Godoy

Structures Department, National University of Cordoba

Casilla de Correo 916, Cordoba 5000, Argentina

A direct procedure for the evaluation of imperfection sensitivity in bifurcation problems is presented. The problems arise in the context of the general theory of elastic stability for discrete structural systems, in which the energy criterion of stability of structures and the total potential energy formulation are employed. In cases of bifurcation buckling the sensitivity of the critical load with respect to an imperfection parameter e is singular at the state given by e =0, so that, a regular perturbation expansion of the solution is not possible. In this work we describe a direct procedure to obtain the relations between the critical loads, the generalized coordinates at the critical state, the eigenvector, and the amplitude of the imperfection, using singular perturbation analysis. The expansions are assumed in terms of arbitrary powers of the imperfection parameter, so that both exponents and coefficients of the expansion are unknown. The solution of the series exponents is obtained by searching the least degenerate solution. The formulation is here applied to asymmetric bifurcations, for which explicit expressions of the coefficients are obtained. The use of the method is illustrated by a simple example, which allows consideration of the main features of the formulation.

Keywords: Buckling, sensitivity analysis, imperfections, singular perturbations

Introduction

Imperfection--sensitivity is a central topic in the theory of elastic stability. The influence that imperfections in the geometry or in the load have on some bifurcation buckling problems has been acknowledged since the pioneering work of Koiter (1945) in the context of a general theory of structural stability. Shells and other slender structures with unstable post--buckling behavior are sensitive to the presence of small imperfections, and bifurcation behavior typical of such structural forms in their idealized or perfect configurations is lost when imperfections are considered.

One important aspect of the behavior is what levels of reduction occur in the maximum load l^M as a function of imperfection amplitude e. A plot l^M -e is called an imperfection--sensitivity plot, and may have the general form illustrated in Figure 1. Many researchers have noticed that such plot may be singular at the state e = 0, i.e. the slope becomes infinite because the curve is tangential to the load axis.

The accepted approach to find imperfection sensitivity when some derivatives are not available has been as follows: a regular perturbation analysis has been carried out in terms of another parameter for which there is no singularity at e = 0, for example a displacement component q₁. Thus expansions of l^Ml^M (q₁), = (q₁) are found, where l^M is the critical load in the imperfect system and q_j is the displacement vector at the critical state. The perturbation parameter in this case is one of the components of the displacement vector for which it is possible to obtain regular perturbation expansions of the other variables. The next step is to explicit the above expansions in such a way that the independent parameter becomes e not q₁. This is done by Thompson and Hunt (1973) by inverting the series so that l^M = l^M (e) can be computed.

It is surprising to find that this indirect approach has been the only one present in the theory. This may be seen in several important texts on the general theory of elastic stability (Croll and Walker, 1972; Thompson and Hunt, 1973; Huseyin, 1975; El Naschie, 1990; Bazant and Cedolin, 1991) to find that they all reproduced the regular perturbation approach. A shortcome of the results mentioned above is not only a problem of approximation, but also that expansions for sensitivity of the eigenvector = ( e ), and sensitivity of the displacement field at the critical state, = ( e ) are not available.

But rather than using regular perturbations to solve a problem with a singularity, it is more convenient to investigate the possibility of employing singular perturbations from the beginning of the analysis. The first work in this direction was presented for one degree of freedom systems (Godoy and Mook 1995). Singular perturbations were employed by expanding the variables of interest in power series of e but with unknown fractional exponents and coefficients. The results showed differences between the classical approach using regular perturbations and the analysis using singular perturbations. In a further contribution, the authors presented a methodology to identify the exponents of the series based on singular perturbations (Banchio and Godoy, 1997). Singular perturbations analysis has been applied in several fields of mechanics, and a recent review may be found for example in the work of Kuzmina (1997).

The present paper concentrates on the imperfection-sensitivity analysis of multi degree of freedom systems which display asymmetric bifurcation. A consistent formulation using singular perturbations is presented, which does not require the inversion of a series, and allows computation of first and higher order sensitivity terms.

Total Potential Energy Formulation

Let us investigate a discretized elastic structural system, for which it is possible to write the total potential energy in the form

where q_i (with i=1,...,n) are the generalized coordinates of the system, and l is the load parameter. For cases in which the energy is linear in the load parameter, one can write V as

where u(q_i )is the internal strain energy, and x(q_i) represents the load potential for a unit value of the load parameter.

Next we study the sensitivity of such system with respect to imperfections. These are assumed in either of two forms: First, they can be represented by a term added to Eq. (2.1) in the form

where the new parameter e is the amplitude of the imperfection with a given space distribution. Examples of such imperfections are eccentric loads.

In the second type of imperfection, the new terms added to the energy, are independent of l and have the form

Examples of imperfections which are modeled in this way are geometric deviations, or those due to a small second load. Notice that the second case is independent of the main load parameter l. More complex changes in the total potential energy could be present in an imperfect system, but only the simplest cases are studied here.

The imperfect system is now represented by the following energy

A perfect case, on the other hand, is given by V (q_i, l,0).

A convenient way to write the energy V is by means of a Taylor expansion about an equilibrium state e

where the coefficients

represent the derivatives of V evaluated at the equilibrium state, and are assumed to be linear in the load l and imperfection e parameters, according to Eqs. (2.2) and (2.3).

The equilibrium state is obtained from the condition of first derivatives of the energy with respect to the generalized coordinates q_i, i.e.

A distinct critical state is characterized by the existence of a unique critical direction, and satisfies the eigenvalue problem

where x_jc is the critical direction, and is the tangent stiffness matrix, with V_ij=V_ji.

The critical state of the perfect system can be identified from the simultaneous solution of Eqs. (2.5) and (2.6) for e =0, leading to the critical displacements q_ic, the eigenvalue (critical load) l_c, and the eigenvector (critical direction) x_jc. In this work, the eigenvector x_jc is normalized using the condition that one of the components has a unit value, and the rest are scaled proportionally. For example, one may use the condition x_1c=1.

Imperfection Sensitivity Via Singular Perturbations

An imperfection changes the equilibrium path, so that a new critical state occurs along the new path. Since we cannot in principle predict at this stage the nature of this new critical state, we shall identify it by the displacement at the critical state, , the load at this state, l^M, and the critical direction .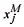

Sensitivity of the new critical state with respect to the imperfection parameter e is given by relations in the form (e),l^M (e), and 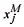(e). The main purpose of this work is to obtain sensitivity expressions using perturbation expansions starting from the perfect case, e = 0. Notice that regular perturbations cannot deal with problems of bifurcations, since the derivatives at e = 0 have an infinite value.

Let us assume such relations in the form of singular perturbations

where the exponents a₁, b₁, g₁ are unknown positive rational numbers; and the coefficients of the series l₁ , q_j1 and xj1 (for j=1, ..., n) are real numbers. The coefficients do not have the meaning of derivatives of the energy V, as they would in regular perturbation analysis.

In singular perturbation analysis, one has to find the values of the exponents first, and then proceed with the values of the coefficients. First we introduce the expansions (3.1) into the equilibrium equations (2.5) with an imperfection given by Eq. (2.2), and obtain the perturbed equilibrium equations by collecting terms with alike powers of e

where ( )’=¶ ( )/¶l; ( )= ¶( )/¶e; ( )’=¶( )/¶e¶ l; and ( )^c indicates evaluation at the critical state c=(q_ic, l_c,0).

Notice that the first term is zero because it represents the equilibrium equation of the perfect system.

To obtain Eq. (3.2) we introduced an imperfection which could be associated to an eccentricity in the load, and extensions to geometrical imperfections would be given by a small modification due to the introduction of Eq. (2.3). In the latter case terms involving derivatives of V with respect to the load and imperfection parameter simultaneously are zero.

Next we obtain the perturbed stability equation by introduction of Eq. (3.1) into Eq. (2.6), leading to

Again, the first term is zero because it represents the stability equation of the perfect system.

The above equations will not be sufficient to obtain the exponents and coefficients of the series, and we also need to include the contracted perturbation equations of equilibrium and stability. The contracted form is obtained by multiplication of an equation by the eigenvector in the perfect system, as described by Thompson and Hunt (1973).

The contracted equilibrium equation results in

Notice that the term associated to e^b1is zero because of the condition of critical state in the perfect system.

A similar procedure is followed to obtain the contracted form of the stability condition:

Here the term associated to e^g1 is zero because of the condition of critical stability of the perfect system.

The set of equilibrium equations (3.2), contracted equilibrium (3.4), stability equations (3.3), and contracted stability equation (3.5), allows computation of the unknown exponents and coefficients.

The search for the first order exponents a₁, b₁, and g₁ in the perturbation equations can be done in several ways

• First, one can employ a search based on trial and error of different sets of exponents. The correct solution is identified as the only set of values of a₁, b₁, and g₁ which lead to the "least degenerate" solution. Such procedure is explained in Godoy and Mook (1995).

• For a one degree of freedom problem one can employ a special geometric device known as a Newton diagram, as explained by Kritskii (1996).

• An alternative consists in the exploration of what exponents lead to the largest number of terms of the same order in the perturbation equations; such technique is explained by Banchio and Godoy (1997).

We shall not emphasize in this paper the identification of possible exponents, since this was done in the works mentioned above, and will investigate common cases in bifurcation analysis.

Asymmetric Bifurcation

First Order Sensitivity

From an identification of all possible exponents (Banchio and Godoy, 1997) we explore in this section the case given by the exponents a₁ = b₁ =1/2 for which the critical state will be shown to represent an asymmetric bifurcation. Such exponents satisfy the condition of least degenerate solution.

Equilibrium Equation

Let us substitute a₁ = b₁ =1/2 into the equilibrium equation (3.2) and collect terms with alike powers in e; then we get

From the main term in this equation, associated to the lowest power of e, we obtain the following condition

The solution q_j1 can be written in the form

where y_j1 is the solution of

Because is of rank n-1, the solution of the above equation requires that should be orthogonal to the critical direction x_ic, i.e.

Stability Equation

The stability equation (2.6) with a₁ = b₁ = g₁ =1/2 results in

The main terms, associated to e^½ yield a condition for x_j1

Contracted Equilibrium Equation

Next we introduce the exponents a₁ and b₁ in the contracted equilibrium equation (3.4) and collect terms with alike powers of e to obtain

The first term is zero due to the above condition (4.4) and the critical stability condition of a perfect system. The main term in the contracted equilibrium equation is thus associated to e. Substitution of q_ji from Eq. (4.2) leads to a quadratic equation in terms of k₁ and l₁

A second condition involving the same variables will be obtained from the contracted stability equation.

Contracted Stability Equation

Contraction of the stability condition (3.5) yields

In the main term we substitute q_ji from Eq. (4.2) to get

which is a second condition in terms of k₁ and l_1. Eq. (4.8) means that the right hand member in Eq. (4.6) is orthogonal to the critical direction x_ic, so that it allows the computation of x_j1.

With the values of k₁ and l₁ obtained from (4.7) and (4.8), one can compute q_ji using Eq. (4.2). Finally, we obtain x_j1 using Eq. (4.6).

Notice that to obtain non-zero values of k₁ and l₁ from Eqs. (4.7) and (4.8) we require

These are the conditions required to obtain an asymmetric bifurcation using the present formulation (Flores and Godoy, 1992).

Second Order Sensitivity

The second order sensitivity can be obtained from Eq. (3.1), in which we already know the first order solution

Here we should evaluate the exponents a₂, b₂, and g₂; and the coefficients l₂, q_j2, and x_j2.

The procedure is similar to that employed for first order sensitivity. To compute the coefficients l₂, q_j2, and x_j2 we employ again the equilibrium and stability equations and their contracted forms.

First, we introduce the expansions (4.12) in the equilibrium Eq. (2.5) and collect terms with alike powers in e leading to

The first two terms are zero because they were already solved in the equilibrium equation of the perfect system and in the equilibrium equation to get the first order coefficients. The main term is now associated to e, which is the remaining part in the first order equilibrium equation.

By trial and error, or by identification of possible exponents, we seek a₂ and b₂ larger than 1/2 so that the new unknowns are involved in the main term multiplied by e. Thus, using the procedure developed by the authors (Banchio and Godoy, 1997) we obtain a₂ =1 and b₂ =1.

The expansions (4.12) are introduced in the stability equation, to get

The main term in this equation is the error term from the first order analysis, and g₂ should be such that provides an equation for x_j2. From there we get g₂ =1.

We now proceed to obtain the coefficients l₂, q_j2, and x_j2 in Eqs. (4.12).

Equilibrium Equation

We substitute a₂ = b₂ =1 into the equilibrium Eq. (4.13), rearrange terms according to the powers of e, and get

From the main term one obtains the following condition

The solution q_j2 can be written as

where y_j2 and are the solution of the following systems of linear equations

The above equations have a solution because the right hand members are orthogonal to x_ic (due to Eq. (4.3) and to the first order contracted equation of equilibrium respectively).

Stability Equation

Eq. (4.14) with a₂ = b₂ = g₂ =1 yields

From the main term we get a condition for x_j2, i.e.

where x₁₂=0 due to the normalization chosen for x_jc.

Contracted Equilibrium Equation

Contraction of the equilibrium Eq. (4.13) and substitution of a₂ and b₂ yields

Terms associated to powers 0 and 1/2 have not been included because they are zero and were considered in the previous section when we worked with the equilibrium equation.

The first term, associated to e, is zero because of Eq. (4.3), the first order contracted equilibrium equation, Eq. (4.4), and the critical stability condition of the perfect system. The main term results associated to the power 3/2.

Next q_j2 is replaced from Eq. (4.15) leading to

This is a linear condition in terms of k₂ and l₂, and a second condition will be identified in the following.

Contracted Stability Equation

The contracted stability equation becomes

The main term with q_j2 from Eq. (4.15) leads to a linear scalar equation in terms of l₂, and k₂

If this equation is satisfied, the right hand side of Eq. (4.16) becomes orthogonal to the critical direction x_ic, so that we can assure that a solution will be obtained for x_j2.

The values of k₂ and l₂ are computed using Eqs. (4.18) and (4.17), and then values of q_j2 and x_j2 result from Eqs. (4.15) and (4.16).

An Algorithm for Asymmetric Bifurcation

A summary of the above developments is next presented in the form of an algorithm to facilitate the computations

First Order Sensitivity

1. Solve

2. Compute

where ( )^1/2+is the positive root.

3. Compute

4. Evaluate

5. Solve

Second Order Sensitivity

1. Solve

2. Compute

with

3. Evaluate

4. Solve

The final results up to second order imperfection sensitivity can be written as

Example of Asymmetric Bifurcation

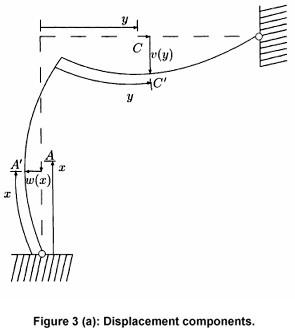
A classical example to illustrate asymmetric bifurcation behavior is a plane frame first studied by Roorda (1965) and analyzed by Koiter (1967) and Thompson and Hunt (1973). The frame is shown in Fig. 2(a), with inextensible bars of length l and bending stiffness B, and a rigid joint at the node where the load P is applied vertically. Pin ends are assumed. In the imperfect configuration there is an eccentricity e l of the point of application of the load. The imperfect system deflects as shown in Fig. 2(b). It is assumed that the magnitude and direction of the load remain the same during the deformation of the structure.

Energy Formulation

The displacement components are identified in Fig. 3, in which w represent the out-of-plane displacements in the vertical member, and v in the horizontal bar. This problem has been solved using finite elements based on the present formulation. Each bar is discretized using N finite elements and N+1 nodes. Each node has the out-of-plane and the rotation degree of freedom. At the pin joints only the rotation is a degree-of-freedom. At the joint between the two bars we employ the end-shortening S¹ and S². The total number of degrees-of-freedom q_i is ( 4N-1). The interpolation functions are cubic polynomials, so that there is a discontinuity in the second derivatives of the nodal transverse displacements The basic formulation follows the work of Thompson and Hunt (1973) and is here repeated for the sake of completeness.

For the h-element in the vertical bar and with as the independent coordinate, we have

A similar expression is obtained for the horizontal bar, as a function of v and g.

The curvature c of an element is

where a dot indicates derivative with respect to .The strain energy of an element becomes

The end-shortening of the h-element is given by

The end-shortening of the bars results in

The total potential energy becomes

or else

where i extends from 1 to (4N-1), and a =1 or 2.

In the perfect system one has e =0, and the necessary derivatives are

where

This problem admits a trivial fundamental path, i.e. q_ic=0. The critical load results from the eigenvalue problem

The lower four eigenvalues for increasing number of elements employed in the discretization are shown in Table 1, together with an analytical value due to Koiter (1967).

The asymmetric bifurcation state results as c=(q_ic=0, l_c, e =0).

Sensitivity Analysis. The sensitivity analysis is carried out using the algorithm presented in this paper, in which the critical load is

with e a negative value. Sensitivity has been computed by different finite element meshes. Convergence of the coefficients for different number of elements is presented in Table 2.

The displacement vector at the critical state shows sensitivity with e in the form

The coefficients have been computed, and for three elements per bar the results are

Notice that with the results available in the literature only sensitivity of the critical load was possible, while the present singular perturbation analysis can also handle sensitivity of all variables at the critical state. Sensitivity of the eigenvector

( e ) results for second order perturbation analysis as

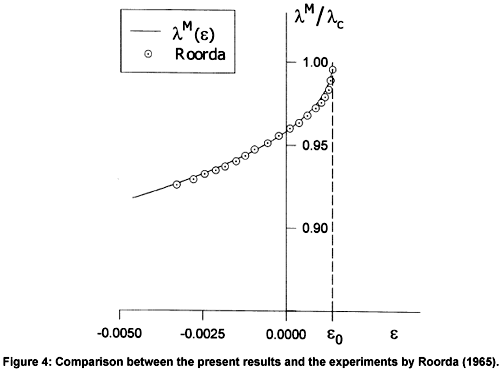
The results of experiments carried out by Roorda together with our theoretical predictions of the second order imperfection analyses are shown in Fig. 4.

Conclusions

A singular perturbation analysis for the imperfection sensitivity of bifurcation problems in buckling of structures has been presented. The methodology develops the required expansions from the beginning of the analysis, so that the solution obtained is what is required to draw an imperfection sensitivity diagram, i.e. how the maximum load changes with the amplitude of the imperfection. The technique is valid for both geometric and load imperfections.

In the proposed expansions, the maximum load, displacements at the critical state, and eigenvector are written as a power series of the amplitude of the imperfection, but with unknown exponents and coefficients. The solution is obtained first, in terms of the exponents, and then for the coefficients. The evaluation of the exponents can be done by trial en error, so as to get the least degenerate solution (Godoy and Mook, 1995), or by geometrical procedures, such as those described by Banchio and Godoy (1997). For the evaluation of the coefficients of the expansions it is necessary to employ the equilibrium and stability conditions, and the contracted forms of both of them. The formulation is specialized for asymmetric bifurcation in this paper, but a similar procedure can be followed for symmetric bifurcation problems with imperfections. It is shown that first, second and higher order perturbation analyses are possible in a rigorous way.

An example is considered to illustrate the details of the implementation. More general problems with larger number of degrees of freedom follow exactly the same procedure. One of the advantages of the present technique is that the solution is obtained in a direct form, without having to invert series and eliminating the possibility of errors and approximations due to the inversion of non-linear problems. Second, it can be employed for higher order perturbation analysis than the available indirect techniques. Third, there is a clear identification of what we seek at each step, and how the variables are found. Fourth, the technique is general and can be applied in cases for which there are no available results, such as trifurcations and problems with mode interaction. These are seen as subject of further research.

Acknowledgments

This work was supported by grants from the Science and Technology Research Council of Argentina (CONICET), the Science Research Council of Cordoba (Agencia Cordoba Ciencia), and the Research Secretary of the National University of Cordoba (SECYT-UNC). L. A. Godoy is a researcher of CONICET.

Manuscript received: October 1999. Technical Editor: Átila P. S. Freire.

• Banchio, E. G. and Godoy L. A., 1997, "Sensibilidad de estados críticos en inestabilidad estructural via perturbaciones singulares", Revista Internacional para Calculo y Diseño en Ingeniería, Vol. 13.
• Bazant Z. and Cedolin L., 1991, "Stability of Structures", Oxford University Press, Oxford.
• Croll J. G. A. and Walker A. C., 1972, "Elements of Structural Stability", Macmillan, London.
• El Naschie M. S., 1990, "Stress, Stability and Chaos in Structural Engineering: An Energy Approach", McGraw-Hill, London.
• Flores F. G. and Godoy L. A., 1992, "Elastic post-buckling analysis via finite element and perturbation techniques, Part 1: Formulation", Int. J. Numerical Methods in Engineering, Vol. 33, pp. 1775-1794.
• Godoy L. A. y Mook D. T., 1995, "Higher-order sensitivity to imperfections in bifurcation buckling analysis", Int. J. Solids Structures, Vol. 33(4), pp. 511-520.
• Huseyin A. H., 1975, "Non-Linear Theory of Elastic Stability", Noordhoff, Leyden, The Netherlands.
• Kuzmina L. K., 1997, "Singularly perturbed system in mechanics: Theory and applications", In Applied Mechanics in the Americas, Vol. 5, The University of Iowa Press, Iowa City, pp. 223-227.
• Kritskii A. B., 1996, "Construction of branching solutions in a study of the stability of thin-walled structures", International Applied Mechanics, Vol.32(5), pp. 58-68.
• Koiter W. T., 1945, "On the Stability of Elastic Equilibrium", in Dutch, Thesis, Delft, Published by H. J. Paris, Amsterdam.
• Koiter W. T., 1967, "Post - buckling analysis of a simple two-bar frame", In: Recent Progress in Applied Mechanics (Eds. B. Broberg, J. Hult, and F. Niordson), Almquist and Wiksell, Stockholm.
• Roorda J., 1965, "Stability of structures with small imperfections", J. Engng. Mech. Div. Am. Soc. Civ. Engrs, Vol. 91, pp. 87.
• Thompson J. M. T. and Hunt G. W., 1973, "A General Theory of Elastic Stability", Wiley, London.

Publication Dates

• Publication in this collection
  28 Sept 2001
• Date of issue
  2001

History

• Received
  Oct 1999