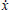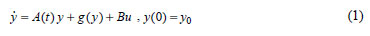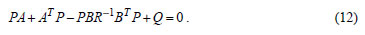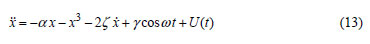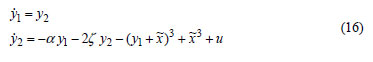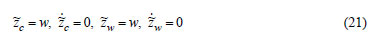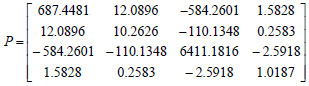An optimal linear control design for nonlinear systems

TECHNICAL PAPERS

An optimal linear control design for nonlinear systems

Marat Rafikov^I; José Manoel Balthazar^II; Ângelo Marcelo Tusset^III

^[e-mail], UFABC and UNIJUI, Dep. de Física, Estatística e Matemática, C.P. 560, 98700-000 Ijui, RS, Brazil

^IISenior Member, ABCM, [e-mail], UNESP, Dep. de Estatística, Matemática Apli. e Comp., C.P. 178, 13500-230 Rio Claro, SP, Brazil

^[e-mail], UnC, Dep. de Ciência da Computação, 89460-000 Canoínhas, SC, Brazil

ABSTRACT

This paper studies the linear feedback control strategies for nonlinear systems. Asymptotic stability of the closed-loop nonlinear system is guaranteed by means of a Lyapunov function, which can clearly be seen to be the solution of the Hamilton-Jacobi-Bellman equation thus guaranteeing both stability and optimality. The formulated Theorem expresses explicitly the form of minimized functional and gives the sufficient conditions that allow using the linear feedback control for nonlinear system. The numerical simulations the Duffing oscillator and the nonlinear automotive active suspension system are provided to show the effectiveness of this method.

Keywords: optimal control, nonlinear system, duffing oscillator, active suspension system, chaotic attractor

Introduction

Since the first publications (Krasovskii, 1959), (Kalman and Beltram, 1960) and (Letov, 1961), in the early 1960s, the Lyapunov function techniques have been used in studying optimal control problems.

It is well known that the nonlinear optimal control problem can be reduced to the Hamilton-Jacobi-Bellman partial differential equation (Bryson and Ho, 1975). There are many difficulties in its solution, in general case. There are, in current literature (see, for example, Bardi and Capuzzo-Dolcetta, 1997), several methods that may be used in obtaining a numerical solution of the Hamilton-Jacobi-Bellman partial differential equation. In particular case, the quadratic Lyapunov function is a solution of the Hamilton-Jacobi-Bellman equation for the linear system with the quadratic functional. In recent years, the idea that a Lyapunov function for the nonlinear system can be an analytical solution of the Hamilton-Jacobi-Bellman equation has become popular.

In Bernstein (1993) a unified framework for continuous-time nonlinear-nonquadratic problems was presented in constructive manner. The results of Bernstein (1993) are based on the fact that steady-state solution of the Hamilton-Jacobi-Bellman equation is a Lyapunov function for the nonlinear system thus guaranteeing both stability and optimality.

In Haddad et al. (1998) the framework developed in Bernstein (1993) was extended to the problem of optimal nonlinear robust control. There are no systematic techniques for obtaining the Lyapunov functions for general nonlinear systems in this case, but this approach can be applied to systems for which the Lyapunov functions can be found.

In Rafikov and Balthazar (2004) the nonquadratic nonlinear Lyapunov function was proposed to resolve the optimal nonlinear control design problem for the Rössler system.

This paper studies the linear feedback control strategies for nonlinear systems.

Asymptotic stability of the closed-loop nonlinear system is guaranteed by means of a Lyapunov function, which can clearly be seen to be the analytical solution of the Hamilton-Jacobi-Bellman equation thus guaranteeing both stability and optimality. The formulated Theorem expresses explicitly the form of minimized functional and gives the sufficient conditions that allow using the linear feedback control for nonlinear system.

Nomenclature

A = bounded matrix (nxn)

B = constant matrix (nxm)

b_s = damping force, N/m/s

= damping force linear, N/m/s

= damping force nonlinear, N/m/s

= damping force symmetric, N/m/s

g = vector (nx1)

G = matrix (nxn)

k_s = suspension stiffness, N/m

= suspension stiffness linear, N/m

= suspension stiffness nonlinear, N/m

k_t = tyre stiffness, N/m

m_s = sprung mass, kg

m_u = unsprung mass, kg

P = Riccati equation (nxn)

Q = matrix (nxn)

V = Lyapunov function

t = time, s

x = displacement of the flexible beam, m

= velocity of the flexible beam, m/s

= acceleration of the flexible beam, m/s²

y = state vector

z_c = vertical displacement of the sprung mass , m

ż_c = vertical velocity of the sprung mass , m/s

_c = vertical acceleration of the sprung mass , m/s²

z_w = vertical displacement of the unsprung mass , m

ż_w = vertical velocity of the unsprung mass , m/s

_w = vertical acceleration of the unsprung mass , m/s²

z_r = disturbance caused by road irregularities, m

Greek Symbols

α = stiffness parameter, N/m

ζ = viscous damping coefficient, N/m/s

γ = amplitude external input, m

ω = angular frequency, rad/s

Γ = neighborhood

Subscripts

s sprung

u unsprung

t tyre

Superscripts

l linear

nl nonlinear

y symmetric

Linear Design for Nonlinear System

We consider the nonlinear controlled system

where y

ⁿ is a state vector, A(t)

^n×m is a bounded matrix, which elements are time dependent, B

^n×m is a constant matrix, u

^m is a control vector, and g(y)

ⁿ is a vector, which elements are continuous nonlinear functions, g(0) = 0.

We remark that the choice of A(t) is not unique, and this influences the performance of the resultant controller.

Assume that:

where G(y)

^n×n is a bounded matrix, which elements depend on y. If we assumed (2), the dynamic system (1) has the following form:

Next, we present an important result, concerning a control law that guarantees stability for a nonlinear system and minimizes a nonquadratic performance funcional.

Theorem 1. If there exist matrices Q(t) and R(t), positive definite, being Q symmetric, such that the matrix:

is positive definite for the bounded matrix G , then the linear feedback control:

is optimal, in order to transfer the non-linear system (3) from an initial to final state:

minimizing the functional:

where the symmetric matrix P(t) is evaluated through the solution of the matrix Ricatti differential equation:

satisfying the final condition:

In addition, with the feedback control (5), there exists a neighborhood Γ₀Γ, Γ

ⁿ , of the origin such that if y₀Γ₀ , the solution y(t) = 0, t > 0, of the controlled system (3) is locally asymptotically stable, and J_min = P(0) y₀.

Finally, if Γ =

ⁿ then the solution y(t) = 0, t > 0, of the controlled system (3) is globally asymptotically stable.

Proof. Lets consider the linear feedback control (5) with matrix P determined by equation (8) which transfers the nonlinear system (3) from an initial to a final state (6), minimizing the functional (7) where the matrix need to be determined.

According to the Dynamic Programming rules one knows that if the minimum of functional (7) exists and if V is a smooth function of the initial conditions, then it satisfies the Hamilton-Jacobi-Bellman equation (Bryson and Ho, 1975):

Considering a function:

where P(t) is a symmetric matrix positive definite and it satisfies the differential Riccati equation (8).

Note that the derivative of the function V, evaluated in the optimal trajectory with control given by (5) is:

Then, substituting in the Hamilton-Jacobi-Bellman equation (10) one obtains:

Then:

Note, that for positive definite matrices and R, the derivative of the function (11) is given by = - y^T y - u^T Ru , and, it is negative definite. Then, the function (11) is Lyapunov function, and the controlled system (3) is locally asymptotically stable. Integrating the derivative of the Lyapunov function (11) given by = - y^T

y - u^T Ru along the optimal trajectory, we obtain J_min = P(0) y₀

Finally, if Γ =

ⁿ , global asymptotic stability follows as a direct consequence of the radial unboundedness condition for the Lyapunov function (11) .

We remark that according to the optimal control theory of linear systems with quadratic functional (Anderson and Moor, 1990) the solution of the nonlinear differential Riccati equation (8) is positive definite and symmetric matrix P > 0 for all R > 0e Q > 0 given, one can conclude the Theorem proof.

If the time interval is infinite and A, B, Q and R are matrix with constant elements, the positive defined matrix P is the solution of the nonlinear, matrix algebraic Riccati equation

Linear Design for Duffing Oscilator

We will apply the proposed method to the Duffing oscillator that is one of the paradigms of nonlinear dynamics.

The Duffing oscillator with the control law U(t) is described by the following nonlinear differential equation:

where α is the stiffness parameter, ζ > 0 is the viscous damping coefficient, γ and ω are the amplitude and frequency of the external input, respectively.

For α < 0 , the Duffing oscillator without control can be interpreted as a model of a periodically forced steel beam which is deflected toward the two magnets, as shown in Fig. 1.

Let the desired trajectory be a function (t) . Then the desired regimen is described by the following equation:

where is a control function which maintains the Duffing oscillator in the desired trajectory. If the function (t) is a solution of equation (13) without the control term then = 0.

Subtracting (14) from (13) and defining:

we will obtain the following system:

where u = U - is feedback control.

So the equation (3) in this case has the following form:

Let the desired trajectory be a periodic orbit:

and the parameters α = -1, ζ = 0.125, γ = 1 and ω = 1.

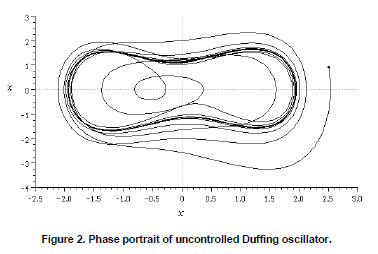
These are exactly the same desired trajectory and parameters as reported by Sinha et al. (2000). For these parameters, the system (14) without control possesses a chaotic attractor, shown in Fig. 2.

Choosing and R = [1], then one obtains by solving the Riccati equation (12) using the LQR function in MATLAB^®. By evaluating the , one has:

where φ(y₁,) = (y₁ + )² + (y₁ + )+ ².

Note that the function φ(y₁, ) has its minimum value in because = 2y₁ + 3₁ = 2 > 0 , then and, admitting 3 > || > 1 , one can evaluate as:

Finally, we can conclude that the optimal function u has the following form:

The phase portrait behavior of the controlled Duffing oscillator is presented in Fig. 3.

Linear Design for Nonlinear Automotive Active Suspension System

Consider a quarter vehicle model that captures the fundamental features of the suspension design of the vehicle. A typical quarter-car suspension system is shown in Fig. 4.

In this figure, m_srepresents the sprung mass, which corresponds to 1/4 of the body mass, and the unsprung mass m_urepresents the wheel at one corner. The parameters k_t ; k_s ; b_sare the tyre stiffness, the suspension stiffness, and the damping rate of the suspension, respectively. The control signal u is generated by the actuator, z_c and z_w denote the vertical displacement of the sprung mass and the unsprung mass, respectively. The disturbance w is caused by road irregularities.

Several methods to solve the active suspension problem have been proposed. The most part of these research contributions are based on linear time-invariant suspension models for control design.

Thompson (1976) was the first to explore the use of optimal control techniques to design an active law.

Active suspension design, using linear parameter varying control, was considered by Gaspar et al. (2003).

The real physical systems always include nonlinear components which must be taken into consideration. The suspension force generated by the hydraulic actuator is inherently nonlinear; the dynamic characteristics of suspension components, i.e., dampings and springs, have nonlinear properties.

To resolve the active suspension problem for nonlinear system in this work we will apply the linear feedback control design above considered.

The equations of motion of the vehicle active suspension system are (Gaspar et al., 2003):

Here, parts of the nonlinear suspension damping b_sare , 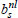and .

The coefficient affects the damping force linearly, and describes the symmetric behavior of the characteristics. Parts of the nonlinear suspension stiffness k_s are a linear coefficient and a nonlinear one .

Considering that the disturbance w, which is caused by road irregularities, have a constant value, the desired trajectory is:

Noting that the desired trajectory is a solution of the system (20) without control and defining:

we will obtain the following equation in form of (1):

where:

Considering:

where:

we present the equation (23) in form (3).

The proposed linear feedback design procedure has been applied to the quarter car suspension with the following values of the parameters (Gaspar et al., 2003): m_s = 290kg , m_u = 40kg , = 23500N/m, = 2350000N/m , k_t = 190000 N/m , = 700 N/m/s e = 400 N/m/s .

For these parameters the matrix A has the following form:

Choosing , R = [0.00001] , then one obtains:

by solving the Riccati Eq. (12).

Finally, we can conclude that the optimal function u has the following form:

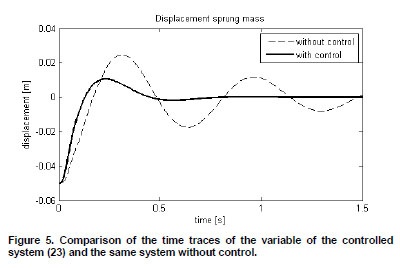
For numerical simulations the disturbances of the initial conditions y₁ = -0.05 m and y₃ = -0.05 m were considered. Fig. 5 and 6 show y₁ and y₃ variations without and with control (25), respectively.

It is difficult to analyze the matrix analytically in this case. Fig. 7 shows the positive function L(t) = y^T

y , calculated in optimal trajectory.

Conclusions

The optimal linear feedback control strategies for nonlinear systems were proposed. Asymptotic stability of the closed-loop nonlinear system is guaranteed by means of a Lyapunov function which can clearly be seen to be the solution of the Hamilton-Jacobi-Bellman equation thus guaranteeing both stability and optimality.

The formulated Theorem expresses explicitly the form of minimized functional and gives the sufficient conditions that allow using the linear feedback control for nonlinear system.

The numerical simulations for the Duffing oscillator and the nonlinear automotive active suspension system are provided to show the effectiveness of this method.

Finally we note that the proposed method can be applied to a large class of nonlinear and chaotic systems.

Acknowledgements

The work was partially supported by the Brazilian Government agencies CNPq and FAPESP.

Paper accepted July, 2008.

Technical Editor: Marcelo Amorim Savi.

• Anderson, B.D.O. and Moor, J.B., 1990, "Optimal Control: Linear Quadratic Methods", Prentice-Hall, NY.
• Bardi, M. and Capuzzo-Dolcetta, I., 1997, "Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations", Birkhäuser, Boston.
• Bernstein, D.S., 1993, "Nonquadratic cost and nonlinear feedback control", Int. J. Robust Nonlinear Contr. 3, pp. 211-229.
• Bryson, JR., A.E. and Ho, Y. C., 1975, "Applied optimal control: Optimization, Estimation, and Control". Hemisphere Publ. Corp., Washington D.C.
• Gaspar, P., Sazaszi, I. and Bokor, J., 2003, "Active suspension design using linear parameter varying control", International Journal of Vehicle Autonomous Systems, Vol. 1, No. 2, pp. 206-221.
• Haddad, W.M., Chellaboina, V. S. and Fausz, J.L., 1998, "Robust nonlinear feedback control for uncertain linear systems with nonquadratic performance criteria", Systems Control Lett., 33, pp. 327-338.
• Krasovskii, N. N., 1959, "On the theory of optimum control", Appl. Math. Mech., vol. 23, pp. 899-919.
• Kalman, R.E. and Bertram, J.E., 1960, "Control system analysis and design via the second method of Lyapunov", Journal of Basis Engineering, vol. 82, pp. 371-393.
• Letov, A.M., 1961, "The analytical design of control systems", Automation and Remote Control, 22, pp. 363-372.
• Rafikov, M. and Balthazar, J. M., 2004, "On an optimal control design for Rössler system", Phys. Lett., A 333, pp. 241-245.
• Sinha, S.C., Henrichs, J.T. and Ravindra, B.A., 2000, "A general approach in the design of active controllers for nonlinear systems exhibiting chaos", Int. J. Biff. Chaos, 10 (1), pp. 165-178.
• Thompson, A. G., 1976, "An active suspension with optimal linear state feedback", Vehicle System Dynamics, Vol. 5, pp. 187-203.

Publication Dates

• Publication in this collection
  30 Jan 2009
• Date of issue
  Dec 2008

History

• Accepted
  July 2008
• Received
  July 2008