Vibration Analysis of a Magnetoelectroelastic Rectangular Plate Based on a Higher-Order Shear Deformation Theory

Abstract

Free vibration of a magnetoelectroelastic rectangular plate is investigated based on the Reddy's third-order shear deformation theory. The plate rests on an elastic foundation and it is considered to have different boundary conditions. Gauss's laws for electrostatics and magnetostatics are used to model the electric and magnetic behavior. The partial differential equations of motion are reduced to a single partial differential equation and then by using the Galerkin method, the ordinary differential equation of motion as well as an analytical relation for the natural frequency of the plate is obtained. Some numerical examples are presented to validate the proposed model and to investigate the effects of several parameters on the vibration frequency of the considered smart plate.

Keywords:
Free vibration; magnetoelectroelastic smart plate; elastic foundation; Reddy's third order shear deformation theory

1 INTRODUCTION

Magnetoelectroelastic composite materials are a new class of smart materials which exhibit a coupling between mechanical, electric and magnetic fields and are capable of converting energy among these three energy forms. These materials have direct application in sensors and actuators, control of vibrations in structures, energy harvesting, etc.

Static and dynamic responses of piezoelectric plates have been investigated extensively in the past years (Alibeigloo and Kani, 2010; Behjat et al., 2011; Rezaiee-Pajand and Sadeghi, 2013; Ghashochi-Bargh and Sadr, 2014; Rafiee et al., 2014; Padoina et al., 2015). Moon et al. (2007) designed a linear magnetostrictive actuator using Terfenol-D to control structural vibration. Hong (2007) studied the thermal vibration of magnetostrictive material embedded in laminated plate by using the generalized differential quadrature method. Later, the same author (2010) used the generalized differential quadrature method to compute the transient response of the laminated magnetostrictive plates under thermal vibration.

Pan (2001) studied multilayered magnetoelectroelastic plates analytically for the first time and derived exact solutions for three-dimensional magnetoelectroelastic plates. Pan and Heyliger (2002) derived analytical solutions for free vibrations of these smart plates. Pan and Heyliger (2003) studied the response of multilayered magnetoelectroelastic plates under cylindrical bending. Ramirez et al. (2006a) presented an approximate solution for the free vibration problem of two-dimensional magnetoelectroelastic laminated plates. Ramirez et al. (2006b) also determined natural frequencies of orthotropic magnetoelectroelastic graded composite plates by using a discrete layer model. Liu and Chang (2010) derived a closed form expression for the transverse vibration of a magnetoelectroelastic thin plate and obtained the exact solution for the free vibration of a two-layered BaTiO₃-CoFe₂O₄ composite. Single-layer approaches to static and free vibration analysis of magnetoelectroelastic laminated plates have also been introduced (Milazzo 2012, 2014a, 2014b; Milazzo and Orlando, 2012). Chen et al. (2014) studied the free vibration of multilayered magnetoelectroelastic plates under combined clamped/free boundary conditions. Moita et al. (2009) presented a higher-order finite element model for static and free vibration analyses of magnetoelectroelastic plates. Based on the nonlocal Love's shell theory, Ke et al. (2014) developed an embedded magnetoelectroelastic cylindrical nanoshell model to study the vibration response of these structures. Razavi and Shooshtari (2014) used Donnell shell theory to analyze the free vibration of magnetoelectroelastic curved panels. Li and Zhang (2014) studied the free vibration of a magnetoelectroelastic plate resting on a Pasternak foundation based on the Mindlin theory. Piovan and Salazar (2015) presented a one-dimensional model for dynamic analysis of magnetoelectroelastic curved beams. Based on three-dimensional elasticity theory, Xin and Hu (2015) derived semi-analytical solutions for free vibration of simply supported and multilayered magnetoelectroelastic plates. Nonlinear free and forced vibration of one-layered and multilayered magnetoelectroelastic rectangular plates based on the classical and first order shear deformation theory have also been investigated (Shooshtari and Razavi 2015a, 2015b; Razavi and Shooshtari, 2015). (Li et al. 2014, 2015) investigated dynamic response of magnetoelectroelastic nanoplate and nanobeam based on nonlocal Mindlin theory and nonlocal and Timoshenko beam theories, respectively. Ansari et al. (2015) developed a nonlocal geometrically nonlinear beam model for magnetoelectroelastic nanobeams subjected to external electric voltage, external magnetic potential and uniform temperature rise. Recently, Shooshtari and Razavi (2015c) investigated large amplitude vibration of laminated magnetoelectroelastic doubly-curved panels.

According to the published articles, there is not any study dealing with analytical study of free vibration of these smart plates based on a higher-order shear deformation theory. So, this study fills the gap in the analysis of magnetoelectroelastic rectangular plates. In this paper, free vibration of simply-supported, clamped and simply-supported/clamped magnetoelectroelastic rectangular plates resting on an elastic foundation is investigated based on the Reddy's third-order shear deformation theory. The Galerkin method is implemented to reduce the partial differential equation of motion to anordinary differential equation and then an analytical relation is obtained for the natural frequency. Some numerical examples are presented to validate the proposed model and to investigate the effects of several parameters such as foundation parameters, plate geometry, and the applied electric and magnetic potentials on the natural frequency of the considered smart plate.

2 THEORETICAL FORMULATION

Consider a rectangular plate resting on an elastic foundation with dimensions of a ×b ×h as shown in Figure 1.

Figure 1:
Schematic of a magnetoelectroelastic plate on an elastic foundation.

Based on the Reddy's third-order shear deformation theory, the displacement field of a composite plate is given as (Reddy, 2004):

Where u₀, v₀, and w₀ are the displacements of the mid-surface along x, y, and z directions, respectively, and θ_x and θ_y are the rotations of a transverse normal about they andx directions, respectively.

The linear strain-displacement relations based on the displacement field given in Eq. (1) are (Reddy, 2004):

Assuming that the electric and magnetic fields are applied along z-direction, the constitutive equations of a magnetoelectroelastic material can be written in the following form (Pan, 2001; Li and Zhang, 2014):

where {σ_x σ_y σ_xz σ_yz σ_xy}^T is stress vector; {D_x D_y D_z}^T and {B_x B_y B_z}^T are the electric displacement and magnetic flux vectors, respectively; [C_ij], [η_ij] and [μ_ij] are the elastic, dielectric and magnetic permeability coefficient matrices, respectively; [e_ij], [q_ij] and [d_ij] are the piezoelectric, piezomagnetic and magnetoelectric coefficient matrices, respectively; and ϕ and ψ are electric and magnetic potentials.

By neglecting in-plane inertia effects (i.e., ) and assuming a constant value for the density of the plate, the equations of motion of a rectangular plate can be expressed in the following form (Reddy, 2004):

where kw and ks are spring and shear coefficients of the elastic foundation, respectively and:

in which ρ0 is the density of the material of the plate and the force and moment resultants are obtained by:

To express Eqs. (6) - (10) in terms of displacements and rotations, the resultants must be calculated from Eq. (12). To this end, σαβ and σαz can be substituted from Eq. (3). However, since ϕ,z and ψ,z are unknown parameters, Eqs. (4) and (5) along with Gauss's laws for electrostatics and magnetostatics, i.e.,

are used which results in:

where

Integrating the relations of Eq. (14) with respect to z, one obtains:

Whereϕ0, ϕ1, ψ0 and ψ1 are constants of the integration and are obtained by using the magnetoelectric boundary conditions on the two surfaces of the plate.

The magnetoelectroelastic body is poled along the z direction and subjected to an electric potential V0 and a magnetic potential Ω0 between the upper and lower surfaces of the plate. So, the magnetoelectric boundary conditions are stated as:

Eqs. (17) and (18) give ϕ0 = V0/h and ψ0 = Ω0/h. Then the gradients of electric and magnetic potentials are obtained from Eq. (16):

Now, the resultants are obtained by Eqs. (3), (12) and (19):

Substituting Eqs. (20) - (23) into Eqs. (6) - (10) yield:

where Li (i=1,2,...,37) are constant coefficients which are functions of applied electric and magnetic potentials, foundation parameters, and material and geometrical properties of the plate and are given in ^{Appendix A}.

It can be seen that Eqs. (24) and (25) are decoupled from Eqs. (26) - (28). So, to study the transverse motion of the plate, it is sufficient to consider only Eqs. (26) - (28). Eqs. (27) and (28) constitute a set of linear equations in terms ofθx andθy. Algebraic solution of this equations results in:

Where Ai (i=1,...,6) are partial differential operators and are defined in ^{Appendix B}.

Substituting Eq. (29) into (26) one obtains the following partial differential equation for the transverse motion of the magnetoelectroelastic plate:

which is expressed in terms of w0.

Three boundary conditions are considered in the present study, which are simply-supported, clamped and combination of simply-supported and clamped edges, that is:

The transverse displacement for each of these boundary conditions can be obtained by:

in which

where (m,n) denotes the mode of vibration and W(t) is unknown function in terms of time (t).

Substituting Eqs. (32a) - (32c) into Eq. (30) and employing the orthogonality of trigonometric functions, the following ordinary differential equationis obtained for each boundary condition:

in which the terms containing d4W/dt4 and d6W/dt6 are neglected. In this equation, Meq and Keq are the equivalent mass and stiffness of the system, respectively.

3 RESULTS

To validate the present study, some numerical examples are presentedand the results are compared with the published ones. As a first comparison, an isotropic simply-supported square plate is considered and the dimensionless frequencies for different length-to-thickness ratios are obtained. The dimensionless frequencies are obtained by using ω = ω0(a2/h), where E is the Young's modulusof the plate and ω0 = (Keq/Meq)1/2 is the circular natural frequency. The results are shown in Table 1 and compared with the results of Vel and Batra (2004) based on the three-dimensional approach, Hosseini-Hashemi et al. (2011) based on the third-order shear deformation plate theory, and Kianiet al. (2012) based on the first-order shear deformation theory. It is seen that there is acceptable accuracy for the thick case (a/h = ) and perfect agreements for the relatively thick (a/h = 10) and the thin (a/h = 50) plates areobserved.

Table 1:
Comparison of dimensionless fundamental frequency of asimply-supportedsquare plate (ν = 0.3).

As a second comparison, a simply-supported isotropic thin plate with different aspect ratios is considered. The dimensionless frequencies are obtained by ω = ω0a2 in which D is the flexural rigidity and D=Eh³/(12(1-ν²⁾). Table 2 shows the results.

Table 2:
Comparison of dimensionless fundamental frequency of a simply-supportedrectangular plate (ν = 0.3, a/h=1000).

Method	a/b
	0.4	2/3	1.0	1.5	2.5
Leissa (1973)	11.4487	14.2561	19.7392	32.0762	71.5564
Present study	11.4487	14.2561	19.7391	32.0760	71.5537

Table 3 shows first four dimensionless frequencies of clamped (CCCC) and simply-supported/clamped (SCSC) square thin plates. The frequencies are obtained by ω = ω₀(a²/π²⁾ and compared with the values reported by various authors. It is seen that the proposed model predicts the frequencies precisely.

Table 3:
First four dimensionless frequencies of square plates with different boundary conditions (ν = 0.3, a/h=1000).

Method	SCSC			CCCC
	ω1	ω2	ω3	ω4	ω1	ω2	ω3	ω4
Kim et al. (1993)	2.9333	5.5466	7.0242	9.5833	3.6460	7.4362	7.4362	10.9644
Woo et al. (2003)	2.9306	5.5469	7.0208	9.5831	3.6448	7.4373	7.4374	10.9650
Eftekhari and Jafari (2013)	2.9333	5.5466	7.0242	9.5833	3.6460	7.4362	7.4362	10.9643
Present study	2.9219	5.5643	7.0282	9.6122	3.6315	7.4615	7.4615	11.0383

Table 4 shows the dimensionless fundamental frequencies ω = ω₀a² of a square isotropic plate with a/h = 100 resting on an elastic foundation. The dimensionless parameters of the foundation are defined as K_w = k_wa⁴/D and K_s = k_sa²/D. It is observed that the results are in good agreement with the accurate results reported by Hasani Baferani et al. (2011). It is worth noting that the dimensionless shear coefficient (K_s) has more effect on the natural frequency. Moreover, it is observed from Tables 3 and 4 that clamped edges increase natural frequencies.

Table 4:
Dimensionless fundamental frequency of square isotropic plates resting on elastic foundation (ν = 0.3).

(Kw,Ks)	Boundary condition	Method
		Lam et al. (2000)	Hasani Baferani et al. (2011)	Present study
(0,0)	SSSS	19.74	19.7374	19.7320
	SCSC	28.95	28.9441	28.8274
(0,100)	SSSS	41.62	48.6149	48.6101
	SCSC	54.68	54.6742	55.1384
(100,0)	SSSS	22.13	22.1261	22.1209
	SCSC	30.63	30.6229	30.5123
(100,100)	SSSS	49.63	49.6327	49.6279
	SCSC	55.59	55.5811	56.0377

As the last comparison, three piezoelectric, piezomagnetic and isotropic square plates with simply-supported boundary condition are considered and two firstdimensionlessfrequencies of these plates are obtained. Table 5 shows the results. The considered piezoelectric, piezomagnetic and isotropic plates are of BaTiO₃, CoFe₂O₄ and aluminum materials, respectively. The BaTiO₃ (shown with B) and CoFe₂O₄ (shown with F) plates are thick with a = b = 1 m and h = 0.3 m and their material properties are given by Wu and Lu (2009). However, the aluminum plate (shown with Al) is thin with a = b = 300 mm and h = 1 mm.The dimensionless frequencies of BaTiO₃ and CoFe₂O₄ are calculated by using ω = ω₀a where C_max is the maximum value of the stiffness coefficient of the plate, whereas The dimensionless frequencies of aluminum plate are obtained by ω = ω₀a².Again, there is a good agreement between the results.

Table 5:
Dimensionless frequencies of several square plates.

Method	Mode (m,n)
	(1,1)			(2,1)
	B	F	Al	B	F	Al
Ribeiro (2005)	-	-	19.7392	-	-	49.3480
Wu and Lu (2009)	1.2523	1.0212	-	2.3003	1.9747	-
Moita et al. (2009)	1.2629	1.1358	-	2.4649	2.1075	-
Present study	1.2349	1.1048	19.7384	2.2857	1.9571	49.3430

Effects of aspect ratio, and the applied electric and magnetic potentials on the dimensionless fundamental frequencies of a magnetoelectroelastic plate with different boundary conditions are studied and the results are shown in Table 6. The dimensionless frequencies are obtained by ω = ω₀a. The material properties of the magnetoelectroelastic plate are (Li and Zhang, 2014): C₁₁ = 226×10⁹ Nm^-2, C₁₂ = 124×10⁹ Nm^-2, C₂₂ = 216×10⁹ Nm^-2, C₄₄ = C₅₅ = 44×10⁹ Nm^-2, C₆₆ = 51×10⁹ Nm^-2, e₃₂ = e₃₁ = -2.2 Cm^-2, q₃₂ = q₃₁ = 290.2 NA^-1m^-1, η₃₃ = 6.35×10^-9 C²N^-1m^-2,d₃₃ = 2737.5×10^-12 NsV^-1C^-1, μ₃₃ = 83.5×10^-6 Ns²C^-2, and ρ₀ = 5500 kgm^-3.

Table 6:
Dimensionless fundamental frequencies of a magnetoelectroelastic rectangular plate(h = 1 mm, a/h = 10).

Boundary Condition	a/b	V0 (108 V)		Ω0 (106 A)
		0	+1	0	+1
SSSS	0.5	0.343322939	0.343322938	0.343322939	0.343322939
	1.0	0.535860885	0.535860883	0.535860885	0.535860887
	2.0	1.233226423	1.233226400	1.233226423	1.233226453
SCSC	0.5	0.380853054	0.380853053	0.380853054	0.380853055
	1.0	0.774485196	0.774485191	0.774485196	0.774485204
	2.0	2.270502531	2.270502390	2.270502531	2.270502717
CCCC	0.5	0.675570089	0.675570085	0.675570089	0.675570094
	1.0	0.962062272	0.962062261	0.962062272	0.962062287
	2.0	2.342843729	2.342843576	2.342843729	2.342843931

It is noticed that increasing the aspect ratio increases the dimensionless frequency of the magnetoelectroelastic plate. Moreover, Table 6 shows that increasing the electric potential decreases the dimensionless frequency of the magnetoelectroelastic plate whereas magnetic potential increases the dimensionless frequency. It is also noticeable that potentials effects on dimensionless frequency are more significant in plates with higher aspect ratios and plates with clamped edges.

Table 7 shows the effects of a/h ratio and foundation parameters on the dimensionless frequencies of a magnetoelectroelastic square plate. In this table, the dimensionless frequencies are obtained by ω = ω₀a and dimensionless foundation parameters are obtained by 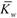= k_wa⁴(C_maxh³⁾ and 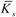= k_sa²(C_maxh³⁾. The magnetoelectric boundary condition is considered to be closed-circuit meaning that in Eq. (18), V₀ = Ω₀ = 0 is substituted. It is seen that a/h ratio tends to decrease the dimensionless frequency. Foundation parameters increase the natural frequencies because the presence of elastic foundation results in the increase of the stiffness of the system. It is also obvious that the dimensionless shear coefficient (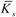) has more effect on the natural frequencies.In addition, it is observed that similar to the results of Tables 3 and 4, clamped edges increase the dimensionless frequencies.

Table 7:
Dimensionless frequencies of a magnetoelectroelastic square plate (h = 1 mm).

Figures 2 and 3 show the effects of shear coefficient of foundation and a/h ratio on the natural frequencies of magnetoelectroelastic plates, respectively. It can be seen that for fixed material and geometric properties, clamped plate has the most natural frequency among the considered plates. Moreover, as it was also shown above, foundation parameter increases the natural frequency whereas the a/h ratio decreases it.

Figure 2:
Effect of shear coefficient of foundation on the fundamental natural frequency of closed-circuit magnetoelectroelastic square plates (a/h = 25, 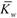= 0).

Figure 3:
Effect of length-to-thickness on the fundamental natural frequency of closed-circuit magnetoelectroelastic square plates (h = 1 mm, 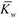= = 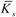0).

4 CONCLUSIONS

In this study, free vibration of a magnetoelectroelastic rectangular plate with different edge supports was investigated analytically. To this end, Reddy's third-order shear deformation theory and Gauss's laws for electrostatics and magnetostatics were used to model the considered smart plate. Galerkin method was applied to the partial differential equation of motion to reduce it to an ordinary differential equation and then an analytical relation was obtained for the natural frequency. Some numerical examples were presented and it was shown that: (a) electric potential decreases the dimensionless natural frequency of the magnetoelectroelastic plate while the magnetic potential increases it, (b) clamped edges increase the dimensionless frequencies of magnetoelectroelastic plate so that the clamped plate has the most dimensionless frequency whereas the simply-supported plate has the least one, and (c) elastic foundation increases the stiffness of the system and consequently increases the natural frequency of the magnetoelectroelastic plate.

References

• Alibeigloo, A., Kani, A.M. (2010). 3D free vibration analysis of laminated cylindrical shell integrated piezoelectric layers using the differential quadrature method, Applied Mathematical Modelling 34(12): 4123-4137.
• Ansari, R., Gholami, R., Rouhi, H. (2015). Size-dependent nonlinear forced vibration analysis of magneto-electro-thermo-elastic Timoshenko nanobeams based upon the nonlocal elasticity, Composite Structures 126: 216-226.
• Behjat, B., Salehi, M., Armina, A., Sadighi, M., Abbasi, M. (2011). Static and dynamic analysis of functionally graded piezoelectric plates under mechanical and electrical loading, ScientiaIranica B 18(4): 986-994.
• Chen, J.Y., Heyliger, P.R., Pan, E. (2014). Free vibration of three-dimensional multilayered magneto-electro-elastic plates under combined clamped/free boundary conditions, Journal of Sound and Vibration 333(17): 4017-4029.
• Eftekhari, S.A., Jafari, A.A. (2013). Modified mixed Ritz-DQ formulation for free vibration of thick rectangular and skew plates with general boundary conditions, Applied Mathematical Modelling 37: 7398-7426.
• Ghashochi-Bargh, H., Sadr, M.H. (2014). Vibration reduction of composite plates by piezoelectric patches using a modified artificial bee colony algorithm, Latin American Journal of Solids and Structures 11(10): 1846-1863.
• Hasani Baferani, A., Saidi, A.R., Ehteshami, H. (2011). Accurate solution for free vibration analysis of functionally graded thick rectangular plates resting on elastic foundation, Composite Structures 93: 1842-1853.
• Hong, C.C. (2007). Thermal Vibration of Magnetostrictive Material in Laminated Plates by the GDQ Method, The Open Mechanics Journal 1: 29-37.
• Hong, CC. (2010). Transient responses of magnetostrictive plates by using the GDQ method, European Journal of Mechanics A/Solids 29(6): 1015-1021.
• Hosseini-Hashemi, S., Fadaee, M., DamavandiTaher H.R. (2011). Exact solutions for free flexural vibration of Lévy-type rectangular thick plates via third-order shear deformation plate theory, Applied Mathematical Modelling 35(2): 708-727.
• Ke, L.L., Wang, Y.S., Yang, J., Kitipornchai, S. (2014). The size-dependent vibration of embedded magneto-electro-elastic cylindrical nanoshells, Smart Materials and Structures 23(12): 125036.
• Kiani, Y., Shakeri, M., Eslami, M.R. (2012). Thermoelastic free vibration and dynamic behaviour of an FGM doubly curved panel via the analytical hybrid Laplace-Fourier transformation, ActaMechanica 223(6): 1199-1218.
• Lam, K.Y., Wang, C.M., He, X.Q. (2000). Canonical exact solutions for Levy-plates on two-parameter foundation using Green's functions, Engineering Structures 22: 364-378.
• Leissa, A.W. (1973). The free vibration of rectangular plates, Journal of Sound and Vibration 31(3): 257-293.
• Li, Y.S., Cai, Z.Y., Shi, S.Y. (2014). Buckling and free vibration of magnetoelectroelastic nanoplate based on nonlocal theory, Composite Structures 111: 522-529.
• Li, Y.S., Ma, P., Wang, W. (2015). Bending, buckling, and free vibration of magnetoelectroelastic nanobeam based on nonlocal theory, Journal of Intelligent Material Systems and Structure doi: 10.1177/1045389X15585899
  » https://doi.org/10.1177/1045389X15585899
• Li, Y., Zhang, J. (2014). Free vibration analysis of magnetoelectroelastic plate resting on a Pasternak foundation, Smart Materials ad Structures 23(2): 025002.
• Liew, K.M., Xiang, Y., Kitipornchai, S., Wang, C.M. (1993). Vibration of thick skew plates based on mindlin shear deformation plate theory, Journal of Sound and Vibration 168(1): 39-69.
• Liu, M.F., Chang, T.P. (2010). Closed form expression for the vibration problem of a transversely isotropic magneto-electro-elastic plate, Journal of Applied Mechanic 77(2): 024502.
• Milazzo, A. (2012). An equivalent single-layer model for magnetoelectroelastic multilayered plate dynamics, Composite Structures 94(6): 2078-2086.
• Milazzo, A. (2014a). Refined equivalent single layer formulations and finite elements for smart laminates free vibrations, Composites Part B 61: 238-253.
• Milazzo, A. (2014b). Layer-wise and equivalent single layer models for smart multilayered plates, Composites Part B 67: 62-75.
• Milazzo, A., Orlando, C. (2012). An equivalent single-layer approach for free vibration analysis of smart laminated thick composite plates, Smart Materials and Structures 21(7): 075031.
• Moita, J.M.S., Soares, C.M.M., Soares, C.A.M. (2009). Analyses of magneto-electro-elastic plates using a higher order finite element model, Composite Structures 91(4): 421-426.
• Moon, S.J., Lim, C.W., Kim, B.H., Park, Y. (2007). Structural vibration control using linear magnetostrictive actuators, Journal of Sound and Vibration 302(4-5): 875-891.
• Padoina, E., Fonseca, J.S.O., Perondi, E.A., Menuzzi, O. (2015). Optimal placement of piezoelectric macro fiber composite patches on composite plates for vibration suppression, Latin American Journal of Solids and Structures 12(5): 925-947.
• Pan, E. (2001). Exact solution for simply supported and multilayered magneto-electro-elastic plates, Journal of Applied Mechanics 68(4): 608-618.
• Pan, E., Heyliger, P.R. (2002). Free vibrations of simply supported and multilayered magneto-electro-elastic plates, Journal of Sound and Vibration 252(3): 429-442.
• Pan, E., Heyliger, P.R. (2003). Exact solutions for magneto-electro-elastic laminates in cylindrical bending, International Journal of Solids and Structures. 40(24): 6859-6876.
• Piovan, M.T., Olmedo Salazar, J.F. (2015). A 1D model for the dynamic analysis of magneto-electro-elastic beams with curved configuration, Mechanics Research Communications 67: 34-38.
• Rafiee, M., He, X.Q., Liew, K.M. (2014). Non-linear dynamic stability of piezoelectric functionally graded carbon nanotube-reinforced composite plates with initial geometric imperfection, International Journal of Non-Linear Mechanics 59: 37-51.
• Ramirez, F., Heyliger, P.R., Pan, E. (2006a). Free vibration response of two-dimensional magneto-electro-elastic laminated plates, Journal of Sound and Vibration 292(3-5): 626-644.
• Ramirez, F., Heyliger, P.R., Pan, E. (2006b). Discrete Layer Solution to Free Vibrations of Functionally Graded Magneto-Electro-Elastic Plates. Mechanics of Advanced Materials and Structures 13(3): 249-266.
• Razavi, S., Shooshtari, A. (2014).Free vibrationanalysis of a magneto-electro elasticdoubly-curvedshellrestingon a Pasternak-typeelasticfoundation, Smart Materials and Structures 23: 105003.
• Razavi, S., Shooshtari, A. (2015). Nonlinear free vibration of magneto-electro-elastic rectangular plates, Composite Structures 119: 377-384.
• Reddy, J.N. (2004). Mechanics of laminated composite plates and shells: theory and analysis, 2nd ed. CRC Press.
• Rezaiee-Pajand, M., Sadeghi, Y. (2013). A bending element for isotropic, multilayered and piezoelectric plates, Latin American Journal of Solids and Structures 10(2):323-348.
• Ribeiro, P. (2005). Nonlinear vibrations of simply-supported plates by the p-version finite element method, Finite Elements in Analysis and Design 41(9-10): 911-924.
• Shooshtari, A., Razavi, S. (2015a). Nonlinear vibration analysis of rectangular magneto-electro-elastic thin plates, IJE transactions A: Basics 28(1): 139-147.
• Shooshtari, A., Razavi, S. (2015b). Large amplitude free vibration of symmetrically laminated magneto-electro-elastic rectangular plates on Pasternak type foundation, Mechanics Research Communications 69: 103-113.
• Shooshtari, A., Razavi, S. (2015c). Linear and nonlinear free vibration of a multilayered magneto-electro-elastic doubly-curved shell on elastic foundation, CompositesPart B 78: 95-108.
• Vel, S.S., Batra, R.C. (2004). Three-dimensional exact solution for the vibration of functionally graded rectangular plates, Journal of Sound and Vibration 272(3-5): 703-730.
• Woo, K.S., Hong, C.H., Basu, P.K., Seo, C.G. (2003). Free vibration of skew Mindlin plates by p-version of FEM, Journal of Sound and Vibration 268(4): 637-656.
• Wu, C.P., Lu, Y.C. (2009). A modified Pagano method for the 3D dynamic responses of functionally graded magneto-electro-elastic plates, Composite Structures 90: 363-372.
• Xin, L., Hu, Z. (2015). Free vibration of simply supported and multilayered magneto-electro-elastic plates, Composite Structures 121: 344-350.

Appendix A

where

Appendix B

Publication Dates

• Publication in this collection
  Mar 2016

History

• Received
  10 Jan 2015
• Reviewed
  17 Aug 2015
• Accepted
  02 Sept 2015