Abstract
Locally resonant acoustic metamaterials have recently attracted a great interest due to their dynamic behaviour, characterized by a band gap at relatively low frequencies. This paper provides a numerical study, by means of finite element modal analyses, of the dynamic properties of 1D mass-in-mass and 2D cellular locally resonant metamaterials. The 2D metamaterial is constituted by a cellular metallic lattice, filled by a soft light material with heavy inclusions or resonators. The influence of material parameters and cell geometry on the band gap width and frequency level are explored. In addition to the usual square lattice we also consider a hexagonal one, which proves to be more efficient for wave filtering.
Keywords
mass-in-mass materials; band gaps; resonant metamaterials
1 INTRODUCTION
Metamaterials are artificial composite man-made materials that, thanks to a special microstructure, exhibit peculiar acoustic, optical or mechanical properties. Metamaterials gain their properties from a rigorous design of low dimensional inhomogeneity, often periodically distributed, rather than from the chemical composition of their components, as found in traditional materials.
Within this broad class, locally resonant acoustic metamaterials (LRAM) exhibit unusual dynamic behavior, with band gaps, i.e. regions where wave propagation is inhibited. Band gaps are also present in some biological structures as in the frustule of diatoms that use this property to provide an efficient light trapping mechanism, Romann et al. (2015) Romann, J., Valmalette, J.-C., Chauton, M. S., Tranell, G., Einarsrud, M.-A., Vadstein, O., (2015). Wavelength and orientation dependent capture of light by diatom frustule nanostructures, Scientific Reports 5:17403. . In artificial LRAM the limit frequencies of the band gap essentially depend on the frequency of the resonators and hence they can provide an effective attenuation of harmonic waves of relatively low frequency, e.g. in the range of some kHz, without requiring very large dimensions as it happens for phononic crystals ( Wu et al., 2007 Wu, Y., Lai, Y., Zhang, Z.-Q. (2007). Effective medium theory for elastic metamaterials in two dimensions. Physical Review B 76:205313(8). ; Croënne et al., 2011 Croënne, C., Lee, E. J. S., Hu, H., Page, J.H. (2011) Band gaps in phononic crystals: Generation mechanisms and interaction effects. AIP Advances 1:041401. ; Hussein et al., 2014 Hussein, M. I., Leamy, M. J., Ruzzene, M., (2014) Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Applied Mechanics Reviews 66:040802-040802-38. ; Miniaci et al., 2015 Miniaci, M., Marzani, A., Testoni, N., De Marchi, L., (2015). Complete band gaps in a polyvinyl chloride (PVC) phononic plate with cross-like holes: numerical design and experimental verification. Ultrasonics 56:251-259. ; Ma and Sheng, 2016 Ma, G., Sheng, P. (2016) Acoustic metamaterials: From local resonances to broad horizons. Science Advances 2:e1501595. ; D'Alessandro et al., 2016 D'Alessandro, L., Belloni, E., Ardito, R., Corigliano, A., Braghin, F., (2016) Modeling and experimental veri_cation of an ultra-wide bandgap in 3D phononic crystal. Applied Physics Letters 109:221907. ). This property can be exploited in different contexts ranging from seismic insulation ( Miniaci et al., 2016 Miniaci, M., Krushynska, A., Bosia, F., Pugno, N. M., (2016). Large scale mechanical metamaterials as seismic shields. New Journal of Physics 18:083041. ) to impact absorbers in small cars ( Comi and Driemeier, 2017 Comi, C., Driemeier, L., (2017). Metamaterials for crashworthiness of small cars, in: AIMETA 2017, Salerno, Italy, 2017. ). Usually LRAMs are composed of a matrix with a periodic arrangement of small resonators wrapped in a soft coating. When the frequency is close to the local resonance frequency of the resonating mass, they absorb and store the kinetic energy, creating a damping mechanism, even without any material dissipation. Figure 1 illustrates a unit cell of a 2D lattice of a LRAM and the one dimensional idealization under the hypothesis that the phase speed of the set core and coating is significantly lower than that of the matrix material.
Sketch of metamaterials with local resonators. (a) 2D unit cell lattice: heavy core (resonator) with soft coating inside a stiff matrix; (b) idealized 1D lattice with internal resonator.
Many researchers have investigated the behavior of these materials. While part of the literature focuses on simple numerical simulations of lumped mass-lumped stiffness models, constructed as series of properly arranged rigid bodies and linear springs ( Huang and Sun, 2009 Huang, H. H., Sun, C. T. (2009). Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New Journal of Physics 11:013003. , Wang, 2014 Wang, X., (2014). Dynamic behaviour of a metamaterial system with negative mass and modulus, International Journal of Solids and Structures, 51:1534-1541. , Tan et al., 2014 Tan, K. T., Huang, H. H., Sun, C. T. (2014) Blast-wave impact mitigation using negative effective mass density concept of elastic metamaterials. International Journal of Impact Engineering 64:20-29. ), a number of works have been devoted to continuum models of LRAMs with their optimization in 2D ( Bacigalupo et al., 2016 Bacigalupo, A., Lepidi, M., Gnecco, G., Gambarotta, L., (2016). Optimal design of auxetic hexachiral metamaterials with local resonators. Smart Materials and Structures 25:054009. ; Krushynska et al., 2014 Krushynska, A. O., Kouznetsova, V. G., Geers, M. G. D., (2014). Towards optimal design of locally resonant acoustic metamaterials. Journal of the Mechanics and Physics of Solids 71:179-196. ), and 3D ( Krushynska et al., 2017 Krushynska, A. O., Miniaci, M., Kouznetsova, V. G., Geers, M. G. D., (2017). Multilayered inclusions in locally resonant metamaterials: two-dimensional versus three-dimensional modeling. Journal of Vibration and Acoustics 139:024501-1-4. ).
In this work we study, by means of finite element modal analysis, the attenuation properties of different LRAMs. First the effect of non-homogeneous resonators distribution in lumped mass-lumped stiffness models on the energy absorption is studied. Then we analyze the band structures of special continuum three-component cellular metamaterials. The geometries consist of square and hexagonal cells, filled by a soft-light material in which cylindrical heavy particles are inserted. Cellular materials are already widely employed in impact absorbers ( Ivanez et al., 2017 Ivanez, I., Fernandez-Canadas, L. M., Sanchez-Saez, S., (2017). Compressive deformation and energy-absorption capability of aluminium honeycomb core. Composite Structures 174:123-133. , Meran and Muğan, 2014 Meran, A. P., Muğan, T. A., (2014). Numerical and experimental study of crashworthiness parameters of honeycomb structures. Thin-Walled Structures 78:87-94. ), but their use as a matrix for locally resonant acoustic metamaterials seems to be new and promising to mitigate the effect of impacts. The effect of including particles of different size within the same cell is also explored. The new configurations here proposed, with different resonators non-symmetrically distributed in the cell, allow to open several bandgaps.
2 ONE DIMENSIONAL WAVE ATTENUATION IN LOCALLY RESONANT METAMATERIALS
2.1 Dispersion equation and related bandgap
To underline the properties of wave attenuation of LRAMs, let us consider first, as in Huang and Sun (2009) Huang, H. H., Sun, C. T. (2009). Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New Journal of Physics 11:013003. , the one dimensional lattice system of Figure 2 , composed by N cells of the type shown in Figure 1 b, spaced by a.
The equations of motion for the unit cell are given by:
If a wave solution is admitted, the displacements of the masses, of a chosen cell ( j), have the form:
where and are the complex wave amplitudes, is the spatial coordinate, is the angular frequency, is the wavenumber. The wave propagation constant is . According to Bloch-Floquet's conditions the displacements in any other cell, at distance is given by:
Substituting eqs. (2) and (3) into eq. (1) , after some numerical manipulations, one obtains the eigenvalue problem:
The eigenvalues are hence found from the so called dispersion equation:
where , and .
For each wave propagation constant , the solution of eq. (5) gives the two vibration frequencies for optical and acoustic waves. Figure 3 shows these frequencies for two different couples of and . Note that there is a gap, i.e. an interval of frequencies where no real solutions exist for any . Rearranging eq. (5) in the form of eq. (6):
Wave dispersion curves for , (blue curves) and , (orange curves). The bandgap between acoustic and optical modes is shaded.
one can show that real solutions , without wave attenuation, do not exists for:
The above condition defines the band gap: the amplitude of waves with frequency inside this band decays as they travel along the lattice. The width of the band gap increases with , as shown in Figure 3 . For high values of , the lower limit of the bandgap tends to 1 and condition (7) coincides with the one given in Huang and Sun (2009) Huang, H. H., Sun, C. T. (2009). Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New Journal of Physics 11:013003. and interpreted as the region where the effective mass of an equivalent single mass lattice is negative. The negative effective mass can explain the unusual dynamic behaviour of structures similar to that of Figure 2 , as shown in the following.
2.2. Dynamic response of different mass-in-mass lattices
The attenuation properties of mass-in-mass lattices are here evidenced numerically. Since the band-gap depends on the eigenfrequency of the resonating mass , see eq. (7) , a specific lattice with a given resonator effectively attenuates waves of frequency close to. Including in a one-dimensional bar different resonators one can in principle attenuate waves of different frequencies. In the present work we consider different lattices with the same matrix of masses kg and stiffness N/m and different resonators A, B and C with the properties listed in Table 1 .
We first analyze through the code LS Dyna the dynamic response of a uniform lattice composed of 2500 identical unit cells, with lattice length mm, subject to an applied displacement , with mm and . The properties of resonator A are chosen for this simulation, see Table 1 .
Figure 4 a and b show the evolution in time of the displacements of the first two nodes and of a node near the end of the bar, for resonator and matrix masses, respectively. From Figure 4 a, one can easily see that the first resonator (top plot) absorbed a big amount of the total energy injected in the system, the second one (middle plot) vibrates at amplitudes considerably smaller and the resonator near the end of the bar (bottom plot) is at rest. The resonators oscillate out of phase with respect to the matrix, the vibration amplitude in the lattice matrix is attenuated and a small amount of energy can reach the end of the bar, see the bottom plot of Figure 4 b.
Vibration amplitude (a) of the mass m2 (resonator) and (b) of mass , for (top plots), (middle plots) and almost at the end of the bar (bottom plots).
Lattice with three zones of different resonators
As proposed in Huang and Sun (2009) Huang, H. H., Sun, C. T. (2009). Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New Journal of Physics 11:013003. , we analyze the response of a uniaxial bar composed of three zones, denoted by A, B and C respectively, each one consisting of 500 unit cells. Each zone has uniform unit mass-in-mass cells with the same mass matrix , and different resonators A, B and C with the properties given in Table 1 . The input displacement in this case is the superposition of three sinusoidal waves with the same amplitude mm and different frequencies,
The frequencies were chosen in such a way that each resonator A, B and C be tuned to attenuate a single frequency of eq. (8) . Assuming , the excitation frequencies were selected: rad/s, rad/s and rad/s. Figure 5 a shows the longitudinal displacement profile for the complete lattice at the end of the analysis, s. The selective damping effect of the three lattices is visible.
Lattice with three zones of different resonators (A, B and C): (a) displacement along the lattice at the end of the analysis s; (b) response, in the frequency domain, in the three regions.
To further clarify this effect, the response at three different locations (one for each lattice region), is represented in the frequency domain in Figure 5 b. In the first region (A) only the lower frequency is attenuated, and, hence, the response has two peaks for rad/s and rad/s; the second (B) and third (C) regions attenuates the subsequent frequencies.
Lattice with three resonators unit cell
We also analyze a further lattice in which a sequence of cells with the three resonators A, B and C is repeated 500 times along the bar. Even though the properties and the total number of resonators is the same of the previous analysis, this different sequence proves to be more effective for wave attenuation, at least in the present case when the excitation contains three harmonics of frequencies very close to those of the resonators. Figure 6 a shows the attenuated displacement along the lattice at the end of the analysis, s. It is noteworthy that the peak value of the displacement is lower than the one of the three-zones lattice, shown in Figure 5 a, and that the first cell with the three different resonators is able to attenuate the three harmonics, therefore only very low values of displacement are present in almost all the bar.
Lattice with three resonators (A, B and C) unit cells: (a) displacement along the lattice at the end of the analysis s, (b) response in the frequency domain, at the middle of the bar.
Figure 6 b presents the response of a lattice in the frequency domain, at the middle of the bar.
3.1. LOCALLY RESONANT CELLULAR METAMATERIALS
3.2. Analysis of free-wave motion
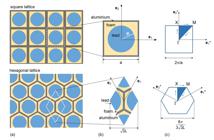
In this section we consider the different two dimensional, three-component, periodic LRAM, represented in Figure 7 a. The lattice is composed by aluminum cells of square or hexagonal shape, filled by a soft, light material, e.g. a polymeric foam, with a heavy circular inclusion. Figure 7 b shows the unit cells of the two materials and the basis vectors and of the direct lattices, is the side of the square, while is the length of the side of the hexagon. The vectors are not unit vectors and, for the hexagonal cell, they are not orthogonal. Each cell within the material is identified by and translations in the and directions. Note that, for the hexagonal lattice, the choice of the quadrangular unit cell, instead of the more natural hexagonal one, proves to be more convenient to impose the Floquet-Bloch periodic boundary conditions.
(a) Sketch of the two LRAMs considered, (b) corresponding unit cell with the vectors of direct lattice ( ), (c) the first Brillouin zone with the vectors of the reciprocal lattice ( ) and the irreducible Brillouin zone (shaded).
Figure 7 c shows the unit cell of the reciprocal lattices which is used to compute the dispersion curves. The points of the reciprocal lattice represent possible wave vectors .
When a wave of angular frequency and wave vector propagates through a periodic material, the solution in terms of displacements u inside a cell j has the form:
where are the complex wave amplitudes and the coordinates of points inside the chosen cell ( ). The displacements of point in any other cell, identified by the integer pair ( ), is given by the Bloch's theorem (see Phani et al., 2006 Phani, A. S., Woodhouse, J., Fleck, N. A., (2006). Wave propagation in two-dimensional periodic lattices, J. Acoust. Soc. Am. 119:1995-2005. ):
where . Due to periodicity, the wave vector can be restricted to the first Brillouin zone of the reciprocal lattice, see Figure 7 c. The vectors of the reciprocal lattice are obtained from the original ones by the orthogonality condition:
For the square lattice the reciprocal unit cell is the square of side while for the hexagonal lattice with side , the reciprocal unit cell is an hexagon with side . Furthermore, due to the symmetries of the reciprocal unit cells, to compute the band-gaps, it is sufficient to consider wave vectors belonging to the boundary of the irreducible Brillouin zone (IBZ), shaded in Figure 7 c, see Kittel (1962) Kittel, C., (1962) Elementary Solid State Physics: A Short Course, 1st Edition, New York, Wiley. . The vertexes of the IBZ identify the couples of q1 and q2 reported in Table 2 .
For any pair within the IBZ, the Bloch's conditions (10) enforce periodicity. The calculation of the frequency can be performed numerically by considering a single unit cell (as in Figure 7 b), by discretizing it into finite elements, and by using (10) to constrain the displacements at its boundary, see Phani et al. (2006) Phani, A. S., Woodhouse, J., Fleck, N. A., (2006). Wave propagation in two-dimensional periodic lattices, J. Acoust. Soc. Am. 119:1995-2005. for details.
In this paper the numerical analyses were performed by the Abaqus code assuming plane strain conditions. We adopted two superposed meshes to treat the real and the imaginary part of the displacements which are involved in the Bloch's boundary conditions. The solutions in the space describe surfaces which are called dispersion surfaces.
3.3. Band-gaps structure of different cellular lattices
We have performed the dispersion analysis, as described above, of several three-component LRAMs of the type shown in Figure 7 . We have considered different dimensions of the square and hexagonal cells, of the resonating core and different materials. The properties of all considered constituent materials are reported in Table 3 .
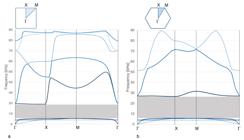
Figure 8 shows the results in terms of frequency versus a scalar pathlength parameter along the boundary of the IBZ for two representative cases, of a square and a hexagonal lattice. The square cell considered is of 8 mm x 8 mm. The walls of the cells are made of aluminum with a thickness of 0.6 mm. The hexagonal cell has a side of 4.6 mm and thickness 0.4 mm. In both cases the cells are filled by a polymeric foam and the internal core is made of lead with radius 3mm. One can observe the presence of a bandgap between the third and fourth mode, from 5.5 kHz and 19 kHz for the square cell and from 5.8 kHz and 26.5 kHz for the hexagonal one.
Dispersion spectrum of in-plane modes in a LRAM: (a) with square lattice (cell b of Table 4 ); (b) with hexagonal lattice.
The first four modes for the square cell are displayed in Figure 9 on a unit cell at the points and of the IBZ. The first mode is a torsional mode characterized by displacements that are almost axisymmetric, which correspond to a rigid rotation of the internal core. The second and third modes are called circumferential modes and and are characterized by a rigid translation of the internal core. These modes have the same frequency at point and can generate a bandgap, with a mechanism similar to that of the mass-in-mass one-dimensional lattice.
In-plane modes in a LRAM: magnitude of the displacement vector for a square unit cell at points × and Ì of the Brillouin zone.
Figure 10 displays the first four modes for the hexagonal lattice at points and of the irreducible Brillouin zone. At point the first two modes are rigid body translations which corresponds to zero frequency, while the third and fourth are a torsional mode circumferential mode . These two modes which are characterized by a rigid rotation and a rigid translation of the internal core, respectively, are better shown on a patch of four cells (shown on the same figure in the rectangular insets).
In-plane modes in a LRAM: magnitude of the displacement vector for a hexagonal unit cell at points à and × of the Brillouin zone.
As discussed by Krushynska et al. (2014) Krushynska, A. O., Kouznetsova, V. G., Geers, M. G. D., (2014). Towards optimal design of locally resonant acoustic metamaterials. Journal of the Mechanics and Physics of Solids 71:179-196. for a different three-component LRAM with rubber-coated inclusions, the width and the location of the band-gap depends on the geometrical properties, in particular on the filling fraction, and on the stiffness and density of the inclusions. In the present work, we have considered the influence of the geometry and materials of the external frame, of the dimensions of the inclusion and of the material filling the cell, on the band-gap.
Figure 11 shows the band gap obtained with several different LRAMs, all of them having the same lead inclusion of radius 3 mm and characterized by the properties listed in Table 4 . The case labeled as “ ” is that previously considered (see Figures 8 a and 9 ) and it is taken as a reference for the discussion. One can observe that the use of a stiffer and heavier material for the external frame (steel instead of aluminum) results in a reduced band gap (cp. cell and ). A similar effect is obtained by increasing the thickness of the frame (as in cell ), while an opposite effect is obtained decreasing the thickness (as in cell ). Comparing cell and one can see that an increase of the size of the cell (i.e., at equal core inclusion, a decrease in the filling fraction) reduces the band-gap, as already evidenced in Krushynska et al. (2014) Krushynska, A. O., Kouznetsova, V. G., Geers, M. G. D., (2014). Towards optimal design of locally resonant acoustic metamaterials. Journal of the Mechanics and Physics of Solids 71:179-196. , and shifts it to lower frequencies.
Bandgap frequencies of different square lattices filled with a light foam with circular lead core of radius mm: external frame of aluminum with different dimensions (a, b, c, e) and steel (d).
Geometry and materials of different LRAMs. In all cases the circular inclusions of lead have radius 3 mm.
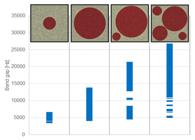
The influence of the radius of the inclusion, and hence of the filling fraction on the resulting bandgap is further shown in Figure 12 . By increasing the radius of the inclusion, at equal external cell, the width of the band gap increases, while the lower limit of it remains almost constant. The shape of the inclusion has a little effect: at equal area of the inclusion the square one shown in yellow in Figure 12 results in a slightly wider band gap.
Bandgap frequencies for varying radius of the circular lead core (in blue) and for a square lead core (in yellow), square aluminum cells of 12mm x 0.6mm.
Figure 13 shows the influence of the shape of the lattice on the band gap. The material with the hexagonal lattice labeled is the same considered in Figures 8 b and 10 . The hexagonal lattices ( and ) and the square lattices ( and ) are endowed by the same global area and also the same area of aluminum frame and of the lead inclusion. One can observe a significant advantage of the hexagonal lattice in terms of band gap width. The properties of the material which fills the cell is also very important: considering a cell filled by a polymeric material, cells and , instead of a foam, cells and (i.e. using a stiffer and heavier filler) one obtains a shift of the band gap to higher frequencies.
Bandgap frequencies for square and hexagonal lattice with different filling materials: in blue foam filler, in orange polyethylene filler.
As proposed in Section 2.2 for the discrete mass-in-mass lattice, we also considered the effect of different resonators within the same LARM. In particular, we studied two square lattices with two and four different circular lead inclusions. The adopted geometries are shown in the insets of Figure 14 . The corresponding band gaps are shown in the same figure. For comparison also the band gaps of the cells with a single small and large inclusion are plotted. One can observe that the multi-resonator cells have a more complex dynamic behavior, characterized by several band gaps and a global increase of filtering frequency range. Hence also in the continuum locally resonant metamaterials the inclusion of different resonator can have a beneficial effect for wave attenuation.
It is worth noting that even if the cells with several resonators loose some of the symmetries of the single resonator cell, the band structure can still be computed by considering the boundary of the IBZ. Figure 15 a shows the dispersion surfaces computed on the whole BZ for the lattice with two resonators and Figure 15 c shows their 2D projection where the band gaps are more clear: their amplitude and position is the same highlight in the dispersion spectrum computed through the IBZ, Figure 15 b.
Square lattice with two different resonators: (a) dispersion surfaces (whole BZ), (b) dispersion spectrum along the boundary of the IBZ, (c) 2D projection of the dispersion surfaces (whole BZ).
4 CONCLUSIONS
This paper provides an extensive numerical study of the attenuation properties of 1D mass-in-mass and 2D cellular LRAM.
For the one dimensional lattice system, the dispersion equation analysis can lead to the so called band gap, characterized by a behavior compatible with the existence of an effective negative mass. In the case of a uniform lattice, a narrow band of frequencies can be attenuated. Two configurations of non-uniform lattices, composed by three different resonators, was numerically studied. The results evidenced that the use of a non-uniform lattice can be an efficient way to enlarge the band gap.
The dispersion properties of different 2D LRAMs were discussed, for in-plane modes. Particularly, we have considered different dimensions of the square and hexagonal cells and of the resonating core, and different materials. According to the analyses, the width and the frequency limits of the band gap strongly depends on the filling fraction, and on the stiffness and density of the core. Moreover, the use of a stiffer and heavier material for the external frame resulted in a reduced band gap. A similar effect is obtained by increasing the thickness of the frame. The adoption of a hexagonal array, analyzed in this paper for three components locally resonant materials, widens the band gap and hence seems to be promising for impact absorption applications.
The elastic wave propagation has been performed in a two dimensional setting, the study in 3D is currently under development.
Acknowledgements
- Financial support of the Italian MIUR (PRIN project nr.2015LYYXA8 on Multi-scale mechanical models for the design and optimization of micro-structured smart materials and metamaterials) and of EU (Erasmus Mundus Programme Smart2) is gratefully acknowledged.
References
- Bacigalupo, A., Lepidi, M., Gnecco, G., Gambarotta, L., (2016). Optimal design of auxetic hexachiral metamaterials with local resonators. Smart Materials and Structures 25:054009.
- Comi, C., Driemeier, L., (2017). Metamaterials for crashworthiness of small cars, in: AIMETA 2017, Salerno, Italy, 2017.
- Croënne, C., Lee, E. J. S., Hu, H., Page, J.H. (2011) Band gaps in phononic crystals: Generation mechanisms and interaction effects. AIP Advances 1:041401.
- D'Alessandro, L., Belloni, E., Ardito, R., Corigliano, A., Braghin, F., (2016) Modeling and experimental veri_cation of an ultra-wide bandgap in 3D phononic crystal. Applied Physics Letters 109:221907.
- Huang, H. H., Sun, C. T. (2009). Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New Journal of Physics 11:013003.
- Hussein, M. I., Leamy, M. J., Ruzzene, M., (2014) Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Applied Mechanics Reviews 66:040802-040802-38.
- Ivanez, I., Fernandez-Canadas, L. M., Sanchez-Saez, S., (2017). Compressive deformation and energy-absorption capability of aluminium honeycomb core. Composite Structures 174:123-133.
- Kittel, C., (1962) Elementary Solid State Physics: A Short Course, 1st Edition, New York, Wiley.
- Krushynska, A. O., Kouznetsova, V. G., Geers, M. G. D., (2014). Towards optimal design of locally resonant acoustic metamaterials. Journal of the Mechanics and Physics of Solids 71:179-196.
- Krushynska, A. O., Miniaci, M., Kouznetsova, V. G., Geers, M. G. D., (2017). Multilayered inclusions in locally resonant metamaterials: two-dimensional versus three-dimensional modeling. Journal of Vibration and Acoustics 139:024501-1-4.
- Ma, G., Sheng, P. (2016) Acoustic metamaterials: From local resonances to broad horizons. Science Advances 2:e1501595.
- Meran, A. P., Muğan, T. A., (2014). Numerical and experimental study of crashworthiness parameters of honeycomb structures. Thin-Walled Structures 78:87-94.
- Miniaci, M., Marzani, A., Testoni, N., De Marchi, L., (2015). Complete band gaps in a polyvinyl chloride (PVC) phononic plate with cross-like holes: numerical design and experimental verification. Ultrasonics 56:251-259.
- Miniaci, M., Krushynska, A., Bosia, F., Pugno, N. M., (2016). Large scale mechanical metamaterials as seismic shields. New Journal of Physics 18:083041.
- Phani, A. S., Woodhouse, J., Fleck, N. A., (2006). Wave propagation in two-dimensional periodic lattices, J. Acoust. Soc. Am. 119:1995-2005.
- Romann, J., Valmalette, J.-C., Chauton, M. S., Tranell, G., Einarsrud, M.-A., Vadstein, O., (2015). Wavelength and orientation dependent capture of light by diatom frustule nanostructures, Scientific Reports 5:17403.
- Tan, K. T., Huang, H. H., Sun, C. T. (2014) Blast-wave impact mitigation using negative effective mass density concept of elastic metamaterials. International Journal of Impact Engineering 64:20-29.
- Wang, X., (2014). Dynamic behaviour of a metamaterial system with negative mass and modulus, International Journal of Solids and Structures, 51:1534-1541.
- Wu, Y., Lai, Y., Zhang, Z.-Q. (2007). Effective medium theory for elastic metamaterials in two dimensions. Physical Review B 76:205313(8).
Publication Dates
-
Publication in this collection
04 June 2018 -
Date of issue
2018
History
-
Received
28 July 2017 -
Reviewed
24 Sept 2017 -
Accepted
01 Oct 2017