Numerical Study on the Projectile Impact Resistance of Multi-Layer Sandwich Panels with Cellular Cores

Abstract

The projectile impact resistance of sandwich panels with cellular cores with different layer numbers has been numerically investigated by perpendicular impact of rigid blunt projectile in ABAQUS/Explicit. These panels with corrugation, hexagonal honeycomb and pyramidal truss cores are impacted at velocities between 50 m/s and 202 m/s while the relative density ranges from 0.001 to 0.15 The effects of core configuration and layer number on projectile impact resistance of sandwich panels with cellular cores are studied. At low impact velocity, sandwich panels with cellular cores outperform the corresponding solid ones and non-montonicity between relative density and projectile resistance of sandwich panels is found and analyzed. Multiplying layer can reduce the maximum central deflection of back face sheet of the above three sandwich panels except pyramidal truss ones in high relative density. Hexagonal honeycomb sandwich panel is beneficial to increasing layer numbers in lowering the contact force and prolonging the interaction time. At high impact velocity, though corrugation and honeycomb sandwich panels are inferior to the equal-weighted solid panels, pyramidal truss ones with high relative density outperform the corresponding solid panels. Multiplying layer is not the desirable way to improve high-velocity projectile resistance.

Keywords:
numerical simulation; projectile impact; multi-layer; sandwich panel; cellular core

1 INTRODUCTION

Cellular materials, due to their excellent properties, find wide use in many different fields such as aerospace, navigation, transport, military and so on. Cellular materials, especially cellular sandwich structures, can effectively lighten and strengthen structural component (Wadley, et al., 2003) and also meet multi-functional requirements (Evans, et al., 2001) including energy absorption (Zhu, et al., 2010; Zhang, et al., 2014), shock cushioning (Xue and Hutchinson, 2004), heat dissipation (Queheillalt, et al., 2008) and sound insulation (Xin and Lu, 2010) due to their unique structure configuration. Being weight-efficient components in aerospace applications, sandwich panels may undergo projectile impact in many situations. For example, fuselages are subjected to impact by hailstones, birds and debris. The resulting impact damage to the sandwich panels ranges from face sheet indentation to complete perforation, which can lead to severe consequence. It makes the study of the projectile impact resistance of sandwich components a significant task.

Much theoretical, numerical and experimental work in dynamic properties including projectile impact resistance of sandwich structures with cellular cores has been taken (Zhu, et al., 2008; Jing, et al., 2011; Yin, et al., 2013; Ni, et al., 2013; Zhang, et al., 2013; Su, et al., 2013; Fan, et al., 2014; Jiang, et al., 2014; Ebrahimi et al., 2016). Liaghat et al. (2010) introduced an analytical model based on energy method to predict the ballistic limit of metallic honeycombs. The results showed that increasing panel thickness and cell wall thickness helps improve the ballistic limit velocity and good agreement was reached with existing experimental data (Goldsmith and Louie, 1995; Nia, et al., 2008). Moreover, configuration of the core will be of importance in determining the dynamic resistance of the sandwich panel (Xue and Hutchinson, 2004; Dharmasena, et al., 2010). Compared with solid panel with the same mass, periodic cores such as honeycomb (Fleck and Deshpande, 2004), corrugation (Rubino, et al., 2009) and pyramidal truss (Yungwirth, et al., 2008) sandwich panels show performance benefits in impact resistance and energy absorption. Furthermore, related to the corresponding empty core, hybrid cores (e.g., metallic lattice-polymer (Yungwirth, et al., 2008), metallic lattice-ceramic (Ni, et al., 2013; Wadley, et al., 2013) and metallic lattice-concrete (Ni, et al., 2015) can offer large potential for enhancing the projectile properties of the sandwich panels.

The above studies are mainly about the impact resistance of single-layer sandwich panels. Liang et al. (2007) have found that the mass distribution between sheet and core significantly affects the performance of single-layer sandwich panels with hexagonal honeycomb, I-core, and corrugated core during water blast loading and that "soft core" designs outperform those with "strong cores". Motivated by this finding in water blast, investigations about the multilayers which can provide appreciable softness due to layer-by-layer crushing have be taken. Wadley et al. (2008) and Dharmasena et al. (2009) have investigated the response of multilayer sandwich panels, referred to pyramidal and prismatic sandwich panels respectively, to underwater shock loading and found that multilayer structures significantly reduce the transmitted pressures of an impulsive load and outperform the single core layer sandwich panels. Xiong et al. (2012) have conducted the quasi-static uniform compression and low-velocity concentrated impact tests and found bi-layer carbon fiber composite pyramidal truss cores have comparable specific energy absorption compared with glass fiber woven textile truss cores. Similar multi-layer structures have been exploited to improve the energy absorption of sandwich panels (Fan, et al., 2013; Kılıçaslan, et al., 2013; Li, et al., 2015). Li et al. (2016) have investigated experimentally and numerically on the response of metallic sandwich panels with stepwise graded aluminum honeycomb cores under blast loading. They found that for the graded panels with relative density descending core arrangement, the core plastic energy dissipation and the transmitted force attenuation were larger than that of the ungraded ones under the same loading condition.

However, so far relatively few studies directly compare the projectile impact resistance of multi-layer sandwich panels with different cellular cores in different relative densities. In this paper, we numerically investigated the projectile impact resistance of sandwich panels with three typical core configurations named corrugation, hexagonal honeycomb and pyramidal truss, with the relatively wide range of relative density from 0.001 to 0.15 and impact velocity from 50 m/s to 202 m/s. Meanwhile, we also studied bi-layer and tri-layer sandwich panels under the above conditions. We analyzed the effects of core configuration and layer number on sandwich panels with the above cellular cores.

2 NUMERICAL SIMULATION

2.1 Finite Element Model and Geometry Parameter

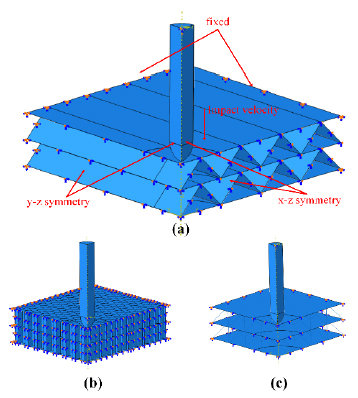
Our finite element (FE) model is established referred to Zhang (2014) in order to compare the FE results and experimental results. Sandwich panels with corrugation, hexagonal honeycomb and pyramidal truss cores are normally impacted by hard hemispherical-nosed projectiles of height h=27.5mm, radius r=3.75mm and mass m ₀=10.4g. The schematic diagram of sandwich panel subjected to projectile impact is shown in Figure 1.

Figure 1:
Schematic diagram of sandwich panel with cellular cores subjected to projectile impact.

The cell schematic diagrams and relative density calculation equations of three kinds of sandwich panels are listed in Table 1. The t_c , b_c , h_c is respectively the thickness, length and height of corrugation cell; hexagonal honeycomb cell has the length l_h and two single-thickness t_h walls and one double-thickness 2t_h wall; t_p and l_p is respectively sectional side width and length of pyramidal truss. The angles between corrugation panel and x-y plane is α_xy = 45º and the angles between pyramidal truss and x, y, z axis are α_x =60º, α_y =60º, α_z =45º. Relative density represents the volume fraction of cellular cell, i.e. corrugation wall, hexagonal honeycomb wall and pyramidal truss, taking up in the whole cell.

Table 1:
Cell schematic diagrams and relative density calculation equations of three kinds of sandwich panels.

Moreover, we increase layer numbers of sandwich panels mentioned above but keep the same surface density ρ_f which is determined by

(1)

where N is the total number of sheets in sandwich structures and ρ is the parent material density which the cellular core uses, i.e. N=2 for single-layer, N=3 for bi-layer and N=4 for tri-layer; H_c is the total height of core which is determined by H_c =kH_ck (k=1,2,3) and H_ck is the height of every single core; h_f is the total thickness of face sheet which is determined by h_f =kh_fk (k=1,2,3) and h_fk is the thickness of every single face sheet. The thickness of corresponding solid panel h_s is calculated by

(2)

Detailed geometry parameters of all three sandwich panels are given in Table 2-5.

Table 2:
Geometry parameters of corrugation sandwich panels.

Table 3:
Geometry parameters of hexagonal honeycomb sandwich panels.

Table 4:
Geometry parameters of pyramidal truss sandwich panels.

Table 5:
Geometry parameters of sandwich panels and corresponding solid panels.

2.2 Material

No.45 steel is used as parent material of projectile and Aluminum 2024-T351 is used as parent material of sheet and cellular core, properties of which are listed in Table 6.

Table 6:
Material parameters for No.45 steel and Aluminum 2024-T351 (Zukas, 1990).

	E (GPa)	v	ρ (kg/m3)	A (MPa)	B (MPa)	n	C	m	D 1	D 2	D 3	D 4	D 5
No.45 steel	209	0.269	7850	/	/	/	/	/	/	/	/	/	/
Aluminum 2024-T351	73	0.33	2780	265	426	0.34	0.015	1	0.13	0.13	1.5	0.011	0

The modified Johnson-Cook constitution relation (Johnson and Cook, 1983) is applied to predict the flow and fracture behavior of the target and the equivalent von Mises stress includes as the effect of three material characteristics namely strain, strain rate, temperature, which reads

(3)

where A, B, C, m, n are material constants given in Table 6. The dimensionless plastic strain rate is defined by is effective plastic strain and

(4)

where ^-1. The dimensionless temperature T^* (Johnson and Cook, 1983) is given by =1s is effective plastic strain rate at a reference strain rate

(5)

where T is actual temperature, T_r and T_m indicate room temperature and melting temperature, respectively. Material damage in the Johnson-Cook model (Johnson and Cook, 1985) is predicted using the following law:

(6)

where ∆ε_p is the increment of equivalent plastic strain during an increment of loading and ε_f is the failure strain as function of three important material characteristics affecting the fracture of the ductile material i.e. stress triaxiality, strain rate and temperature (Johnson and Cook, 1985), which is determined by

(7)

wherein σ^* is the normalizd mean stress which is given by σ^* = σ_m /σ_e and σ_m is hydrostatic pressure and σ_e is equivalent von Mises stress. D ₁, D ₂, D ₃, D ₄ and D ₅ are material constants referred to the experimental results of Zukas (1990), which are listed in Table 6.

2.3 Simulation

We used commercial FE software ABAQUS/Explicit (version 6.10) to carry out 3D FE simulation under projectile impact conditions. Rigid constraint was applied to the projectile. Symmetric boundary constraints about x-z and y-z planes were imposed. The other two sides of sandwich panel were fully clamped. The bonding between front and back face sheets and core was assumed to be perfect which lead to a relatively high evaluation of ballistic resistance of structure due to the ignorance of de-bonding between face sheets and core. General contact was imposed. In order to get the conservation result, friction was ignored in the contact between the components. Continuum shell elements S4R were assigned to solid panel, sheets, corrugation cores and hexagonal honeycomb cores while pyramidal trusses were meshed using beam elements B31 and bullet was assigned solid element C3D8R. At first mesh convergence test was conducted by comparing with the experimental results in Zhang (2014) and the refined seed size 0.5 mm was chosen in the zone next to the projectile and coarser seed size 2 mm was used in other part of both face sheet and core as shown in Table 7. Then step time convergence test was also did as listed in Table 8 and 0.03 ms was chosen as the total time step for hexagonal honeycomb sandwich panel subjected to projectile impact V ₀=202 m/s. The sandwich panel was just penetrated by projectile which was efficient in computing time. The mesh size was the same for other sandwich panels in the following and time step was chosen based on the identical guideline.

Table 7:
Mesh convergence test of single-layer hexagonal honeycomb sandwich panel with = 0.037 based on the experimental result.

Mesh size	Residual velocity(m/s)	CPU time(s)
Core-3mm-Sheet-0.5mm-2mm	176.60	68
Core-1.5mm-Sheet-0.5mm-2mm	176.31	84
Core-0.5mm-Sheet-0.5mm-2mm	178.98	361
Core-0.5mm-2mm-Sheet-0.5mm-2mm	179.09	166
Experiment	178.59	/

Table 8:
Step time convergence test of single-layer hexagonal honeycomb sandwich panel with = 0.037.

Time step(ms)	Residual velocity(m/s)	CPU time(s)
0.3	179.09	166
0.4	179.09	223
0.5	179.09	267
0.6	179.09	352

The finite element model of sandwich panel was depicted in Figure 2. Whereas higher impact resistance of sandwich panel with cellular core can be obtained when the projectile impacts the interaction area of counterparts in cell, the sandwich panels were impacted within the gap of cell to get a conservation result, as illustrated in Figure 2. Zhang (2014) stated that hexagonal honeycomb sandwich panel with V ₀ from 50 m/s to 202 m/s were imposed to projectile. = 0.037 has limited resistance to the projectile with the velocity greater than 250 m/s. Considering the comparison with Zhang's experimental result and meanwhile investigate the response in different impact velocities, range of projectile velocities

Figure 2:
Finite element model of sandwich panel, taking bi-layer sandwich panel for example: (a)corrugation, (b)hexagonal honeycomb and (c)pyramidal truss.

Present analysis was validated with the experimental results (Zhang, 2014) as shown in Figure 3 and 4 and good agreement was reached.

Figure 3:
Residual velocity in the normal impact of the single-layer hexagonal square honeycomb sandwich panel: FE results compared with experimental results.

Figure 4:
Hexagonal honeycomb sandwich panel after projectile impact: (a)front face sheet in experiment (Zhang, 2014), (b)front face sheet in FE, (c)back face sheet in experiment (Zhang, 2014) and (d) back face sheet in FE.

3 RESULT AND DISCUSSION

According to our FE simulation, results are qualitatively presented in two groups: (1) low velocity where the core and back face sheet cannot be perforated; (2) high velocity where sandwich panel can be totally perforated. Furthermore, the projectile impact resistance in low and high velocity can be characterized by ω central deflection of back face sheet and V _r residual velocity of projectile after perforation, respectively (see Figure 5). Effects of core configuration, relative density and layer number on projectile impact resistance are investigated and deformation and failure modes are observed and discussed. For readability, abbreviation are used in figures as the nomenclature that firstly corrug, honey and pyr are referred to corrugation, hexagonal honeycomb and pyramidal truss respectively, secondly number 1/2/3 is referred to layer number, thirdly comes the relative density and finally comes the impact velocity, i.e. corrug-1-002-150 represents the single-layer corrugation sandwich panel with the relative density 0.02 subjected to the projectile with the velocity 150 m/s.

Figure 5:
Different phenomena after projectile impact: (a)deflection of back face sheet and (b) perforation with residual velocity.

3.1 Effect of Core Configuration

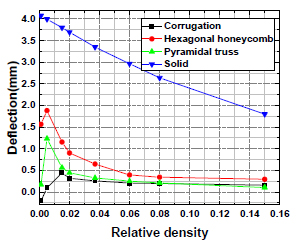
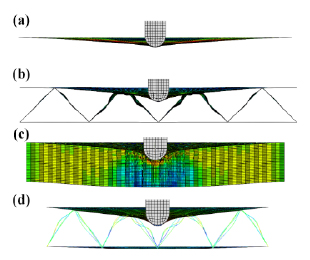
Fleck and Deshpande (2004) have found that the sandwich beam outperforms the monolithic beam with the same mass resulting from the fact that thin front face sheet of the sandwich beam acquires a smaller fraction of the blast impulse compared to the relatively thick monolithic beam. We also compared the sandwich panels with the corresponding solid panels having the same surface density. The deflection versus relative density curves of three kinds of sandwich panels and corresponding solid panels when impact velocity is 50 m/s are shown in Figure 6. It is concluded that sandwich panels have superior resistance in low-velocity projectile impact resistance compared with equal-weighted corresponding solid panels. As depicted in Figure 7, unlike the structural response of solid panel subjected to impact, the core of sandwich panel is crushed after the impulse is transmitted to the front face sheet. Then the plastic bending of core unit cell and stretching of the thin front face sheet make much contribution to the dissipation of impact energy. Therefore, much more plastic dissipation energy can be absorbed by sandwich structures. Based on Table 9, plastic dissipation energy of sandwich structures is 20% to 50% higher than that in solid panels except the corrugated sandwich panel with ≤ 0.005. For these corrugated sandwich panel, core unit cells with the thickness lower than 0.044 mm are so weak that can hardly support the front face sheet during the impact that less energy is dissipated by plasticity though they makes the back face sheet suffer smaller deflection due to their severe deformation.

Figure 6:
Deflection of three kinds of sandwich panels and corresponding solid panel when V ₀=50 m/s.

Figure 7:
Defomation of panel when reaching the maxium deflection during impact when V ₀=50 m/s and ≤ 0.005:(a) solid panel, (b) corrugation sandwich panel, (c) hexagonal honeycomb sandwich panel and (d) pyramidal truss sandwich panel.

Table 9:
Plastic dissipation energy (unit:J) versus relative density of sandwich panels and corresponding solid panels when V ₀=50m/s.

Relative density	Corrugated sandwich panel	Hexagonal honeycomb sandwich panel	Pyramidal truss sandwich panel	Solid panel
0.001	7.87	11.26	11.71	8.59
0.005	8.01	11.30	11.67	8.53
0.015	10.08	11.80	11.71	8.38
0.02	10.57	11.84	11.60	8.33
0.037	11.25	11.71	11.71	8.19
0.06	11.00	11.56	11.75	7.96
0.08	11.02	11.87	11.73	7.74
0.15	11.58	11.19	11.62	7.50

Generally speaking, the impact resistance of structures is beneficial to the high core energy absorption (Jing, et al., 2013; Li, et al., 2014).As depicted in Figure 8, among all three single-layer sandwich panels, back face sheet hardly absorbs energy by plastic dissipation and most of plastic dissipation happen to front face sheet and core and moreover front face sheet dissipates more energy than core. Xue and Hutchinson (2003) concluded that the energy distribution is sensitive to the mass distribution caused by the increasing of relative density. When the core relative density is low i.e. Figure 6. = 0.001, the core is so weak compared with face sheet that it is not able to support the front face sheet such that large area of front face sheet contributes to the plastic dissipation and meanwhile the severe deformation happens to the core. Though the projectile approach forward, small deflection is found to the back face sheet. At higher core relative densities, the face sheet is so weak compared with the core that more energy is dissipated due to the plastic deformation of front face sheet and back face sheet is slightly affected. When it comes to medium core relative density, the face sheet and the core are competitive and the effect of sandwich panel is dominant, so a peak of deflection of bottom face sheet occurs as shown in

Figure 8:
Percentage of plastic dissipation of face sheet and core as the function of relative density: (a) corrugation sandwich panel, (b) square honeycomb sandwich panel and (c) pyramidal truss sandwich panel.

When the impact velocity is between 105 m/s and 202 m/s, almost all the sandwich panel and solid panel are both perforated by the projectile. Shear failure and stretching happen to the face sheet but the core does not dissipate so much energy as that in low velocity. As shown in Figure 9, relatively thick solid panel outperforms the sandwich panel, however pyramidal truss sandwich panel with high relative density shows better projectile impact resistance than solid panel due to its stubby truss.

Figure 9:
Residual velocity of three kinds of sandwich panels and corresponding solid panel when (a) V ₀=188 m/s, and (b) V ₀= 202 m/s.

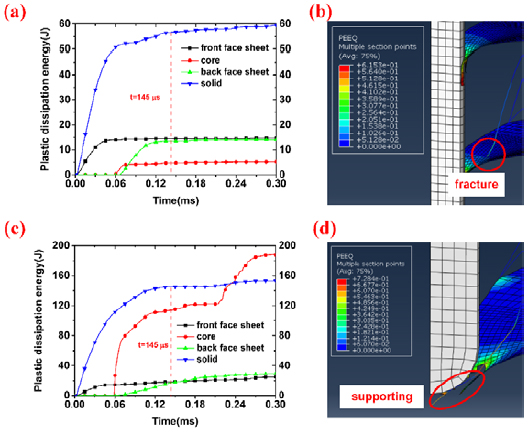
So as to insight the enhancance in projectile resistance in pyramidal truss sandwich panels, plastic dissipation energy of sheets and core at 202 m/s in a lower and a higher relative density named Figure 10. Comparing Figure 10a and 10c, plastic dissipation energy of front and back face sheets of the pyramidal truss sandwich panel with Figure 10b and 10d, though front face sheets in relative density = 0.15 the central pyramidal truss are stronger to provide additional supporting against the impact instead of getting fractured before contacting projectile when = 0.15 during the perforation is nearly the same while core energy-absorption ability quite differs in two relative density. When = 0.02 and = 0.02. = 0.02 and = 0.15 are both sheared in the center, when = 0.02, core-dissipated energy is about 5.2 J and only takes up the 15.4% of total plastic dissipation energy. When = 0.15 and corresponding deformation modes are shown in = 0.15, however, core-dissipated energy is 188 J contributing up to 77.7% to total plastic dissipation energy. As shown in = 0.02 and

Figure 10:
Plastic dissipation energy versus time of sheets and core of pyramidal truss sandwich panels in a lower and a higher relative density and corresponding solid panels when impact velocity V ₀=202 m/s and deformation of pyramidal truss sandwich panels when t= 145μs: (a)(b) 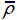= 0.02 and (c)(d) 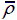= 0.15.

3.2 Effect of Layer Number

In order to investigate how layer number influences the impact resistance of sandwich panels, we have also simulated projectile impact to single-layer, bi-layer and tri-layer sandwich panels in kinds of velocities. Surface density of each kind of sandwich panels are kept the same and detailed parameters are listed in Table 5. As deflection-relative density curves when V ₀=50 m/s are depicted in Figure 11, multi-layer sandwich panels cannot certainly own better impact resistance ability and would even be inferior to single-layer sandwich panels. For example, when Figure 11. It should be noted that for the corrugation sandwich panel with ≥ 0.04, multiplying layers can reduce the deflection of back face sheet of the sandwich panels except pyramidal truss ones with = 0.0001and = 0.02 the deflection of back face sheet of single-layer corrugation sandwich panel is lower than those of the bi-layer and tri-layer ones and the deflection of front face sheet is also in that range i.e. 0.32 mm for single-layer, 0.39 mm for bi-layer and 0.54 mm for tri-layer. When = 0.0005, the deflection of back face sheet is negtive due to the very weak core. = 0.15 as shown in

Figure 11:
Deflection-relative density curves when V ₀=50 m/s (a) corrugation sandwich panels, (b) hexagonal honeycomb sandwich panels and (c) pyramidal truss sandwich panel.

The contact load-time curves of single-layer, bi-layer and tri-layer corrugation sandwich panels when V ₀=50 m/s are depicted in Figure 12, respectively. The appearance of force indicates that the projectile contacts with the front face sheet. With the further impact, the projectile is resisted by corrugatioin cell wall or together with the back face sheet and the contact force increases with fluctuation. After the impact velocity of projectile reduces to zero, the projectile is rebounced due to the recovery of the compressed part and velocity increases until the projectile totally seperates itself from the sandwich panel. At that time, the contact force will reduce to zero. It is shown in Figure 12 that force values of multi-layer corrugation sandwich panels are much lower than single-layer ones in the former half but higher in the later half when Wadley, et al., 2008)(Xiong, et al., 2012)( Kılıçaslan, et al., 2013)(Fan, et al., 2014). Notably, the interaction time before that projectile is rebounded from corrugation sandwich panel is extended by increasing layer numbers in lower relative density Figure 12a) while the interaction time of multi-layer corrugation sandwich panels are much shorter when Figure 12b and 12c). = 0.02 (see = 0.15 (see = 0.08 and = 0.02, = 0.08 and = 0.15 at = 0.02 and = 0.08. Load fluctuation is observed during the interaction and with the bending and progressive deformation of the cell sheets, the force keeps increasing. This phenomenon is also observed by (

Figure 12:
Contact force-time history of corrugation sandwich panels at V ₀=50 m/s when (a) 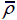= 0.15. 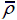= 0.02 , (b) 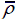= 0.08 and (c)

As to hexagonal honeycomb sandwich panels, increasing layer numbers can not only noticeably lower force values of structures during impact but also prolong interaction time as shown in Figure 13. In pyramidal truss sandwich panel, force values of bi-layer and tri-layer is below the ones in single-layer structure in the former half when Figure 14b and 14c), i.e. when = 0.02, but the force values of multi-layer pyramidal truss during impact are higher and interaction times are much shorter(see = 0.15 it only takes about 0.169 ms to rebound the projectile in tri-layer but the value is 2.81 ms in single-layer. From the perspective of reducing force and prolonging the contact time, the hexagonal honeycomb sandwich panel is the best among the three sandwich panels. This finding will give certain instruction in designing anti-impact sandwich structures.

Figure 13:
Contact force-time history of hexagonal honeycomb sandwich panels at V ₀=50m/s when (a) 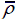= 0.08 and (c) 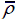= 0.15 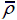= 0.02 , (b)

Figure 14:
Contact force-time history of pyramidal truss sandwich panels at V ₀=50 m/s when (a) 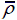= 0.02 , (b) 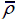= 0.08 and (c) 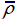= 0.15.

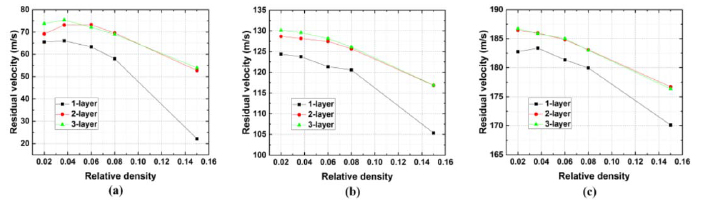
Concerning high velocity namely 105 m/s, 150 m/s and 202 m/s there, increasing layer number cannot enhance the projectile impact resistance of three kinds of sandwich panels as shown in Figure 15-17, though there is a significant positive correlation between relative density and the projectile impact resistance of three kinds of sandwich panels with cellular cores. It is noted that the weaken by increasing layer number is more dramatical in pyramidal truss sandwich panel when V ₀=202 m/s are listed in Table 10. = 0.15. For pyramidal truss sandwich panel when = 0.08 and = 0.15, the pyramidal truss do more contribution in plastic dissipation. When multiplying layer and keeping the same surface density, the thickness of pyramidal truss is reduced and thinner face sheet are more easily sheared by projectile so that multi-layer ones underperform the single-layer ones. Deformation modes after impact of three kinds of sandwich panels when

Figure 15:
Residual velocity of corrugation sandwich panels with different layers when V ₀=(a)105 m/s, (b)150 m/s and (c)202 m/s.

Figure 16:
Residual velocity of hexagonal honeycomb sandwich panels with different layers when V ₀=(a)105 m/s, (b)150 m/s and (c)202 m/s.

Figure 17:
Residual velocity of pyramidal truss sandwich panels with different layers when V ₀=(a)105 m/s, (b)150 m/s and (c)202 m/s.

Table 10:
Deformation modes after impact of three kinds of sandwich panels when V ₀=202 m/s. 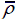= 0.08 and

4 CONCLUSIONS

The numerical simulation study of sandwich panels with cellular cores under projectile impact was performed using ABAQUS/Explicit finite element code. We investigated the effects of core configuration, relative density and layer number on projectile impact resistance in low and high velocity.

In low velocity (50 m/s)

Comparing with corresponding solid panel, sandwich panels with cellular cores have remarkable strength in projectile impact resistance due to their gradual deformation during impact. To get the relatively small deflection of bottom face sheet, either weak cellular core or strong one is admirable choice instead of choosing the cellular core with medium relative density. Considering the actual manufacturing condition, strong core of sandwich panel is preferred. Multiplying layer can reduce the maximum central deflection of back face sheet of the above three sandwich panels except pyramidal truss ones in high relative density. Moreover hexagonal honeycomb sandwich panel is beneficial to increasing layer numbers in lowering the contact force and prolonging the interaction time.

In high velocity (105 m/s to 202 m/s)

Though sandwich panels with cellular cores are inferior to the corresponding solid panels with the same surface density, pyramidal truss sandwich panel outperforms solid panel in high relative density due to the strong supporting of pyramidal truss. Increasing layer number has no help increasing the projectile impact resistance of above three kinds of sandwich panels except the hexagonal honeycomb sandwich panels in high relative density.

Acknowledgements

Supports of National Natural Science Foundation of China under Grant Nos. 11302270 and 11572059, Ph.D. Programs Foundation of Ministry of Education of China under Grant No. 20130191120015, Chongqing Natural Science Foundation under Grant No. cstc2013jcyjA00030 and State Key Lab for Strength and Vibration of Mechanical Structures of Xi׳an Jiaotong University under Grant No. SV2015-KF-12 are gratefully acknowledged.

References

• Dharmasena, K.P., Queheillalt, D., Wadley, H.N.G., Chen, Y.C., Dudt, P., Knight, D., Wei, Z.S. and Evans, A.G. (2009). Dynamic response of a multilayer prismatic structure to impulsive loads incident from water. International Journal of Impact Engineering 36:632-643.
• Dharmasena, K.P., Queheillalt, D.T., Wadley, H.N.G., Dudt, P., Chen, Y., Knight, D., Evans, A.G. and Deshpande, V.S. (2010). Dynamic compression of metallic sandwich structures during planar impulsive loading in water. European Journal of Mechanics A/Solids 29:56-67.
• Ebrahimi, H., Ghosh, R., Mahdi, E., Hashemi, H.N. and Vaziri, A. (2016). Honeycomb sandwich panels subjected to combined shock and projectile impact. International Journal of Impact Engineering 95:1-11.
• Evans, A.G., Hutchinson, J.W., Fleck, N.A., Ashby, M.F. and Wadley, H.N.G. (2001). The topological design of multifunctional cellular metals. Progress in Materials Science 46: 309-327.
• Fan, H.L., Yang, W. and Zhou, Q. (2013). Experimental research of compressive responses of multi-layered woven textile sandwich panels under quasi-static loading. Composites: Part B: Engineering 42:1151-1156.
• Fan, H.L., Zhao, L., Chen, H.L., Zheng. J.J., Jiang, Y.F., Huang, S.Q., Kuang, N. and Ye, C.X. (2014). Dynamic compression failure mechanisms and dynamic effects of integrated woven sandwich composites. Journal of Composite Materials 48:427-437.
• Fleck, N.A. and Deshpande, V.S. (2004). The resistance of clamped sandwich beams to shock loading. Journal of Applied Mechanics-Transactions of the ASME 71:386-401.
• Goldsmith, W. and Louie, D.L. (1995). Axial perforation of aluminum honeycombs by projectiles. International Journal of Solids and Structures 32:1017-1046.
• Jiang, W.Z., Liu, Y., Gu, Y. and Lu, G.X. (2014). An analytical model of a clamped sandwich beam under low-impulse mass impact. Latin American Journal of Solids and Structures 11:1651-1678.
• Jing, L., Wang, Z.H., Ning, J.G. and Zhao, L.M. (2011). The mechanical response of metallic sandwich beams under foam projectile impact loading. Latin American Journal of Solids and Structures 8:107-120.
• Jing, L., Xi, C.Q., Wang, Z.H. and Zhao, L.M. (2013). Energy absorption and failure mechanism of metallic cylindrical sandwich shells under impact loading. Material & Design 52:470-480.
• Johnson, G.R. and Cook, W.H. (1983). A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Proceedings of the 9th International Symposium on Ballistic (ISB-9), Hague, p. 541-547.
• Johnson, G.R. and Cook, W.H. (1985). Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Engineering Fracture Mechanics 21:31-48.
• Kılıçaslan, C., Güden, M., Odacı, İ, K. and Taşdemirci, A. (2013). The impact responses and the finite element modeling of layered trapezoidal corrugated aluminum core and aluminum sheet interlayer sandwich structures. Materials and Design 46:121-133.
• Li, S.Q., Li, X., Wang, Z.H., Wu, G.Y., Lu, G.X. and Zhao, L.M. (2016). Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading. Composites Part A: Applied Science and manufacturing 80:1-12.
• Li, S.Q., Lu, G.X., Wang, Z.H., Zhao, L.M. and Wu, G.Y. (2015). Finite element simulation of metallic cylindrical sandwich shells with graded aluminum tubular cores subjected to internal blast loading. International Journal of Mechanical Sciences 96-97:1-12.
• Li, X., Wang, Z.H., Zhu, F., Wu, G.Y. and Zhao, L.M. (2014). Response of aluminum corrugated sandwich panels under air blast loadings: Experiment and numerical simulation. International Journal of Impact Engineering 65:79-88.
• Liaghat, G.H., Nia, A.A., Daghyani, H.R. and Sadighi, M. (2010). Ballistic limit evaluation for impact of cylindrical projectiles on honeycomb panels. Thin-Walled Structures 48:55-61.
• Liang, Y.M., Spuskanyuk, A.V., Flores, S.E., Hayhurst, D.R., Hutchinson, J.W., McMeeking, R.M. and Evans, A.G. (2007). The response of metallic sandwich panels to water blast. Journal of Applied Mechanics-Transactions of the ASME 74:81-99.
• Ni, C.Y., Hou, R., Xia, H.Y., Zhang, Q.C., Wang, W.B., Cheng, Z.H. and Lu, T.J. (2015). Perforation resistance of corrugated metallic sandwich plates filled with reactive powder concrete: Experiment and simulation. Composite Structures 127:426-435.
• Ni, C.Y., Li, Y.C., Xin, F.X., Jin, F. and Lu, T.J. (2013). Ballistic resistance of hybrid-cored sandwich plates: Numerical and experimental assessment. Composites Part A: Applied Science and Manufacturing 46:69-79.
• Nia, A.A., Razavi, S.B. and Majzoobi, G.H. (2008). Ballistic limit determination of aluminum honeycombs-Experimental study. Material Science and Engineering A 488:273-280.
• Queheillalt, D.T., Carbajal, G., Peterson, G.P. and Wadley, H.N.G. (2008). A multifunctional heat pipe sandwich panel structure. International Journal of Heat and Mass Transfer 51:312-326.
• Rubino, V., Deshpande, V.S. and Fleck, N.A. (2009). The dynamic response of clamped rectangular Y-frame and corrugated core sandwich plates. European Journal of Mechanics A/Solids 28:14-24.
• Su, W., Xiang, Y., Jiang, Y.F., Huang, S.Q., Fan, H.L. and Liu, R.H. (2013). Quasi-static out-of-plane compression of hollow integrated woven textile sandwich composites. Applied Mechanics and Materials 423-426:58-62.
• Wadley, H.N.G., Dharmasena, K.P., Chen, Y.C., Dudt, P., Knight, D., Charette, R. and Kiddy, K. (2008). Compressive response of multilayered pyramidal lattices during underwater shock loading. International Journal of Impact Engineering 35:1102-1114.
• Wadley, H.N.G., Dharmasena, K.P., O'Masta, M.R. and Wetzel, J.J. (2013). Impact response of aluminum corrugated core sandwich panels. International Journal of Impact Engineering 62:114-128.
• Wadley, H.N.G., Fleck, N.A. and Evans, A.G. (2003). Fabrication and structural performance of periodic cellular metal sandwich structures. Composites Science and Technology 63:2331-2341.
• Xin, F.X. and Lu, T.J. (2010). Analytical modelling of fluid loaded orthogonally rib-stiffened sandwich structures: Sound transmission. Journal of the Mechanics and Physics of Solids 58:1374-1396.
• Xiong, J., Vaziri, A., Ma, L., Papadopoulos, J. and Wu, L.Z. (2012). Compression and impact testing of two-layer composite pyramidal-core sandwich panels. Composite Structures 94:793-801.
• Xue, Z.Y. and Hutchinson J.W. (2004). A comparative study of impulse-resistant metal sandwich plates. International Journal of Impact Engineering 30:1283-1305.
• Xue, Z.Y. and Hutchinson, J.W. (2003). Preliminary assessment of sandwich plates subjected to blast loads. International Journal of Mechanical Sciences 45:687-705.
• Yin, S., Wu, L.Z., Yang, J.S., Ma, L. and Nutt, S. (2013). Damping and low-velocity impact behavior of filler composite pyramidal lattice structures. Journal of Composite Materials 48:1789-1800.
• Yungwirth, C.J., Wadley, H.N.G., O'Connor, J.H., Zakraysek, A.G. and Deshpande, V.S. (2008). Impact response of sandwich plates with a pyramidal lattice core. International Journal of Impact Engineering 35:920-936.
• Zhang, G.Q., Wang, B., Ma, L., Xiong, J. and Wu, L.Z. (2013). Response of sandwich structures with pyramidal truss cores under compression and impact loading. Composite Structures 100:451-463.
• Zhang, Q.N. (2014). Study on the Ballistic Impact Effect of Sandwich Panels with Aluminum Honeycomb Cores, Master Thesis (in Chinese), Beijing Institute of Technology, China.
• Zhang, X.C., An, L.Q. and Ding, H.M. (2014). Dynamic crushing behavior and energy absorption of honeycombs with density gradient. Journal of Sandwich Structures and Materials 16(2):125-147.
• Zhu, F., Lu, G.X., Ruan, D. and Wang, Z.H. (2010). Plastic deformation, failure and energy absorption of sandwich structures with metallic cellular cores. International Journal of Protective Structures 1:507-541.
• Zhu, F., Zhan, L.M., Lu, G.X. and Wang, Z.H. (2008). Deformation and failure of blast-loaded metallic sandwich panels-Experimental investigations. International Journal of Impact Engineering 35:837-951.
• Zukas, J.A. (1990). High velocity impact dynamics, John Wiley Sons (New York).

Publication Dates

• Publication in this collection
  Dec 2016

History

• Received
  20 Mar 2016
• Reviewed
  03 Sept 2016
• Accepted
  06 Sept 2016