Investigation of dynamic instability of three plates switch under step DC voltage actuation using modified couple stress theory

Abstract

In this paper dynamical instability of three-layer micro-switch under DC voltage actuation has been studied. Recent studies have used the classical beam theory while leaving out the length scale parameter. In this paper dynamic behavior of the switch has been investigated based on couple stress theory and considering the length scale parameter. To this end, governing dynamic equation of the micro switch has been extracted and presented. Considering the nonlinearity of governing equation due to the existence of electrostatic force, Galerkin method has been implemented to overcome this nonlinearity and solve the mentioned equation and obtain the dynamic response. Dynamic response of micro switch has been investigated with and without considering the damping effects. Variation of dynamic pull-in voltage versus micro beam length and primary gap between micro beam and stationary electrodes have been studied using couple stress and classic beam theory and obtained results have been compared to each other. Also dependency of dynamic pull-in voltage to damping factor has been studied with considering two theories. Furthermore switching time of micro switch have been determined and compared using couple stress and classic beam theories.

Keywords:
micro switch; dynamic instability; electrostatic; couple stress theory; length scale parameter

1 INTRODUCTION

Nowadays micro electro mechanical devices have shown remarkable significance in various industries such as automation, military, medical, telecom. This issue is because of significant advantages of these structures such as small size, low energy consumption, high performance, low manufacturing costs and feasibility for batch fabrication. Simulating the mechanical behavior of these devices, particularly their static and dynamic behavior, is required for design and manufacturing purposes. Therefore, electrostatically actuated MEM/NEM devices such as, micro switches [¹, ²] micro-mirrors [³, ⁴], nano-switches [⁵, ⁶], nano-tweezers [⁷, ⁸], micro capacitors [⁹-¹¹], sensors [¹², ¹³], resonators [¹⁴, ¹⁵] and oscillators [¹⁶, ¹⁷] are widely designed, fabricated, used and analyzed.

The majority of the micro structures perform using electrostatic actuation. The nature of this actuation is nonlinear which results in the nonlinearity of the governing equations. Presence of such nonlinearity along with length scale parameter cause difficulty in analysis with simulation soft wares and may result in deviation of obtained results. Therefore theoretical analysis may be considered as firm technique to examination of mechanical behavior. Precise modeling of micro switch is necessary to obtain accurate behavior of the structures. Length scale parameter is an important parameter which must be considered for analysis of mechanical behavior of micro structures. This parameter is an inherent characteristic of movable part of micro structure (micro beam or micro plate), and if it is less than specific limit, its effects is exposed. Application of classic beam theory (classic elasticity theory) for micro structures with non-negligible length scale parameter may result in inaccurate results. So considering the length scale parameter and application of couple stress theory instead of classic beam theory is an essential issue in the case of mechanical analysis of micro structures. Numerous researches have been done in the case of static and dynamic stability analysis of micro switches without considering this effect [¹⁸-²⁶]. Some works have devoted to analysis of static and dynamic behavior of micro and nano structures considering the length scale parameter. Sedighi et al. [²⁷] modeled static and dynamic pull-in instability of nanoactuator based on the strain gradient theory. Pull-in instability of cantilever and fixed-fixed beam-type nano structure and nano switches using strain gradient and couple stress theory have been studied in refs. [⁵, ⁶, ²⁸, ²⁹]. Keivani et al. [⁷] investigated the instability analysis of nanotweezers using couple stress theory. Rashvand et al. [³⁰-³²] studied size-dependent behavior of circular and rectangular micro-plates.

The dispersion forces play an important role in the instability behavior of nano structures. Although the effects of these forces can be neglected in the modeling of static and dynamic behavior of micro structures. In nano-scale, Tadi Beni et al. [¹⁹] have studied pull-in instability in a torsional nano-actuator considering Casimir force. Vakili et al. [³³], Koochi et al. [²⁰] and Soroush et al. [²²] have studied instability of nano-beams subjected to electrostatic force and considering van der Waals force. Koochi et al. investigated pull-in instability of carbon nano-tube based actuator under the Coulomb force and considering van der Waals attraction [²⁴]. Dequesnes et al. [³⁴, ³⁵] have studied the pull-in phenomena and pull-in voltage of a carbon-based nano-electromechanical switch.

Three layer micro switch is a type of micro structure, in which micro-beam/micro-plate is suspended between two stationary plates. Recently some investigations have been accomplished in the case of static and dynamic stability analysis of these switches. Comprehensive stability analysis of three plate micro switch subjected to electrostatic force has been presented in ref. [³⁶]. Azizi et al. [³⁷] studied bifurcation Behavior of a Capacitive three layer microswitch. Mobki et al. [³⁸] designed and analyzed a new micromachined tunable three layer capacitor with extended tenability. Azimloo et al. [³⁹] Shah-Mohammadi-Azar [⁴⁰] presented Angular Velocity Sensors based three layer switch and studied their pull-in behavior. However most of the related researches are based on overlooking of length scale parameter.

With regard to the importance of dynamic analysis of these switches and considering this effect, this paper is devoted to study the dynamic behavior, instability and pull-in voltage of three layer micro switch with considering length scale parameter and using couple stress theory instead of classic beam theory. Furthermore, the importance of considering or neglecting this effect has been discussed. For this aim, the governing dynamic equation of the micro-switch has been presented. Moreover, due to the nonlinearity of this equation, which is a result of the existence of electro static force, Galerkin method has been implemented for solving the governing equation. In the rest of the paper, the model description, mathematical model of micro switch, obtained results and supplementary discussion for results are presented.

2 MODEL DESCRIPTION

In this section schematic view of studied micro-switch is illustrated in the coming section and the governing equations of the micro-switch will be extracted and presented. Figure 1(a) shows the schematic view of three layer micro switch, in which a micro beam is situated between two stationary electrodes. Initial distance of micro beam to upper and lower electrode is $G_0$. Applied voltages of $V_1$ and $V_2$ are induced from lower and upper electrode to micro beam. These voltages cause to attraction electrostatic force between micro beam and electrodes. If $V_2>V_1$, imposed electrostatic force from upper electrode prevails over imposed force from lower electrode and micro beam bends toward upper electrode and vice versa. If $V_1=V_2$, micro beam is settled in its initial place and does not move toward any electrodes. Figure 1(b) shows the cross section view of the micro switch. $h$ and $b$ indicate thickness and width of micro beam. Micro beam is considered as isotropic media with elastic modulus of $E$, density of $\rho$, length of $L$, cross moment inertia of $I$, cross section of $A$. Parameter $p$ denotes applied voltages ratio and equals with $p=\raisebox{1ex}{$V_2$}\!\left/ \!\raisebox{-1ex}{$V_1$}\right.$.

Figure 1:
schematic view of three layer micro switch

3 MATHEMATICAL MODELING

The governing dynamic equation of the micro switch is obtained and presented in this section.

Based on the couple stress theory strain energy $U$ of an isotropic material with linear elasticity behavior can be presented as [⁴¹]:

$U=\frac{1}{2}\underset{\overline{V}}{\overset{}{{\displaystyle \int }}}\left({\sigma }_{ij}{\epsilon }_{ij}+m_{ij}{\chi }_{ij}\right)d\overline{V}$ (1)

where $\overline{V}$ is the occupied volume of the material. σ, ε, m and 𝜒 are stress, strain, derivative part of couple stress and symmetric part of curvature tensors. Based on the linear elasticity theory, mentioned tensors can be presented as:

${\sigma }_{ij}=\lambda {\epsilon }_{kk}{\delta }_{ij}+2G{\epsilon }_{ij}$ (2)

${\epsilon }_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right)$ (3)

$m_{ij}=2l^{2}G{\chi }_{ij}$ (4)

${\chi }_{ij}=\frac{1}{2}\left({\theta }_{i,j}+{\theta }_{j,i}\right)$ (5)

In this equation 𝜆 and G are Lame constants, l is length scale parameter of material, u and 𝜃 are displacement and rotation vectors. Also correspondence of these vectors is as:

$\theta =\frac{1}{2}curl\left(u\right)$ (6)

Considering the x-z coordinate of Figure 1, which x axis coincide centroidal one; arrays of displacement vectors can be shown in the form of [⁴²]:

$u=-z\psi \left(x,t\right),v=0,w=w\left(x,t\right)$ (7)

Where u, v and w are components of displacement vectors in direction of x, y and z axes respectively. Also rotation angle (𝜓) can be obtained based on the classic beam theory:

$\psi =\frac{\partial w\left(x,t\right)}{\partial x}$ (8)

For plane stress and infinitesimal displacement, the components of strain tensor can be achieved using of Eqs. (3), (7), and (8) as:

$\begin{array}{l}{\epsilon }_{xx}=\frac{\partial u}{\partial x}-z\frac{{\partial }^{2}w}{\partial x^2}\\ {\epsilon }_{yy}=\upsilon z\frac{{\partial }^{2}w}{\partial x^2}\\ {\epsilon }_{zz}=\upsilon z\frac{{\partial }^{2}w}{\partial x^2}\\ {\epsilon }_{xy}={\epsilon }_{yz}={\epsilon }_{xz}=0\end{array}$ (9)

Based on Eqs. (6)-(8) following relations are accurate.

$\begin{array}{l}{\theta }_y=-\frac{\partial w\left(x,t\right)}{\partial x}\\ {\theta }_x={\theta }_y=0\end{array}$ (10)

With substituting Eq. (10) into equation 5, arrays of symmetric curvature tensor can be presented as:

$\begin{array}{l}{\chi }_{xy}=-\frac{1}{2}\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}\\ {\chi }_{xx}={\chi }_{yy}={\chi }_{zz}={\chi }_{xz}={\chi }_{yz}=0\end{array}$ (11)

Similarly the form of stress tensor components can be extracted by substituting of Eq. (9) into Eq. (2).

$\begin{array}{l}{\sigma }_{xx}=-Ez\frac{{\partial }^{2}w}{\partial x^2}\\ {\sigma }_{yy}={\sigma }_{zz}={\sigma }_{xy}={\sigma }_{xz}={\sigma }_{yz}=0\end{array}$ (12)

Arrays of derivative part of couple stress tensor can be obtained by placing of Eq. (11) into Eq. (4):

$\begin{array}{l}{m}_{xy}=-G{l}^2\frac{{\partial }^{2}w}{\partial x^2}\\ m_{xx}=m_{yy}=m_{xz}=m_{yz}=m_{zz}=0\end{array}$ (13)

Strain energy U can be presented as equation 14, with substituting of Eqs. (9), (11), (12) and (13) into equation 1.

$U=-\frac{1}{2}\underset{0}{\overset{L}{{\displaystyle \int }}}{M}_x\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}+Y_{xy}\frac{{\partial }^{2}w\left(x,t\right)}{\partial x^2}dx$ (14)

Where $M_x$ and $Y_{xy}$ indicate resultant and couple moment and are as:

$\begin{array}{l}{M}_x=\int {\sigma }_{xx}zdA\\ Y_{xy}=\int m_{xy}dA\end{array}$ (15)

Kinetic energy also can be shown as Eq. (16):

$T=\frac{1}{2}\underset{0}{\overset{L}{{\displaystyle \int }}}\rho A{\left[\frac{\partial w\left(x,t\right)}{\partial t}\right]}^{2}dx$ (16)

Virtual work of electrostatic force may be assumed as:

$\delta W=\underset{0}{\overset{L}{{\displaystyle \int }}}{q}_{elec}\left(x,t\right)\delta w\left(x,t\right)dx$ (17)

Where $q_{elec}$ indicates induced electrostatic force to micro beam. Based on the Hamilton principal following relation is valid.

$\delta \underset{0}{\overset{t}{{\displaystyle \int }}}\left(T-U+W\right)dt=0$ (18)

Governing dynamic equation of micro beam based on the couple stress theory and taking into account the residual stress and damping effects can be elicited and shown as:

$\left(EI+GA{l}^2\right)\frac{{\partial }^{4}w}{\partial x^4}+c\frac{\partial w}{\partial t}+\rho A\frac{{\partial }^{2}w}{\partial t^2}-N_r\frac{{\partial }^{2}w}{\partial x^2}=q_{elec}$ (19)

Where $N_r={\sigma }_r\left(1-\vartheta \right)bh$ is residual force, and ${\sigma }_r$ and $\vartheta$ are the biaxial effective residual force and Poisson's ratio [²]. Considering the above equation; it is obvious that bending rigidity of micro beam is composed from two terms of EI (bending rigidity based classic beam theory) and GAl2 (bending rigidity caused by considering of length scale parameter effects).

Electrostatic force per length of micro beam can be shown based on the reports of ref [³⁶] as:

$q_{elec}=\frac{b{\epsilon }_0}{2}\left[\frac{V_1^2}{{\left(G_0-w\right)}^2}-\frac{V_2^2}{{\left(G_0+w\right)}^2}\right]$ (20)

Where ${\epsilon }_0=8.854\times {10}^{-12}{C}^2{N}^{-1}{m}^{-2}$ is permittivity coefficient of vacuum. Governing equation of micro beam based on classic beam theory can be extracted by setting $l=0$ in Eq. (20).

The governing dynamic equation of three layer micro-switch subjected to electrostatic force and considering length scale parameter of micro-beam are presented in this section. Due to the nonlinearity of term of electrostatic force, Galerkin method are implemented for dynamic analysis of the micro-switch. This method is proper and reliable one for analysis of static and dynamic behavior of micro and nano-switches. The procedure of Galerkin implementation for solving the Eq. (19) will be extended in the next section.

4 NUMERICAL METHOD

In this section applied numerical approach for solving the Eq. (19) is presented. For this case dynamic displacement can be assumed as:

$w\left(x,t\right)={\displaystyle \sum }_{i=1}^N{q}_i\left(t\right){\psi }_i\left(x\right)$ (21)

Using Galerkin approximation method, the equation of dynamic response has been obtained as [⁴³]:

$\left[M\right]\left[\ddot{q}\right]+\left[C\right]\left[\dot{q}\right]+\left[K\right]\left[q\right]=\left[F\right]$ (22)

Where:

$\begin{array}{l}{\left[M\right]}_{ij}=\rho A\underset{0}{\overset{L}{{\displaystyle \int }}}{\psi }_i\left(x\right){\psi }_j\left(x\right)dx\\ {\left[K\right]}_{ij}=\left(EI+GA{l}^2\right)\underset{0}{\overset{L}{{\displaystyle \int }}}\frac{d^4{\psi }_i\left(x\right)}{d{x}^4}{\psi }_j\left(x\right)dx-N_r\underset{0}{\overset{L}{{\displaystyle \int }}}\frac{d^2{\psi }_i\left(x\right)}{d{x}^2}{\psi }_j\left(x\right)dx\\ {\left[C\right]}_{ij}=c\underset{0}{\overset{L}{{\displaystyle \int }}}{\psi }_i\left(x\right){\psi }_j\left(x\right)dx\\ {\left[F\right]}_{ij}=\underset{0}{\overset{L}{{\displaystyle \int }}}{q}_{elec}{\psi }_i\left(x\right)dx\end{array}$ (23)

Where indicate the effective mass, stiffness, damping, and actuating force matrices respectively. $q\left(t\right)$ can be obtained from above set of ordinary differential equations using an integration scheme.

5 RESULTS AND DISCUSSION

5.1. Validation and Convergence of Numerical Method

This subsection deals with validation of numerical method. For this purpose obtained results of this paper have been compared with those obtained by Hung and Senturia [⁴⁴]. The micro-switch specification are $E=149Gpa$, $\rho =2330\raisebox{1ex}{$kg$}\!\left/ \!\raisebox{-1ex}{$m^2$}\right.$, $L=610\mu m$, $b=40\mu m$, $h=2.2\mu m$, $G_0=2.3\mu m$, ${\sigma }_r=-3.7MPa$, and $p=0$. Calculated pull-in time for various values of applied voltages are shown in Figure 2. As can be seen in this figure, results of this paper are in good agreement with theoretical and experimental results.

Figure 2:
Comparison of the pull-in time for various values of applied voltage

For more validation the obtained results of this paper are compared with those presented in ref [³⁷]. The micro-switch is a fixed-fixed one with $E=169Gpa$, $\rho =2330\raisebox{1ex}{$kg$}\!\left/ \!\raisebox{-1ex}{$m^2$}\right.$, $L=600\mu m$, $b=4\mu m$, $h=2\mu m$, $G_0=2\mu m$, ${\sigma }_r=-3.7MPa$, and $p=0.5$. The results convergence and comparison are shown in table 1. As shown in this table, with increase of N the obtained pull-in voltage converges to 10.11V and presented results are in good agreement with results of ref [³⁷].

Table 1:
Comparison of the pull-in voltage

	Results of ref [37]	This paper (N=1)	This paper (N=2)	This paper (N=3)
Pull-in voltage	10.07	10.12	10.11	10.11

5.2. Dynamic response of micro-switch

In this section obtained results of the dynamic instability of golden micro switch are presented. Physical and spatial properties of the micro switch are shown in table 2. The micro beam is a cantilever gold one.

Table 2:
physical and geometrical properties of studied three layer golden micro switch

properties	value
Length	$400\mu m$
width	$10\mu m$
thickness	$2\mu m$
Young modulus	$98.5GPa$
Shear modulus	$27GPa$
Length scale parameter [45]	$1.05\mu m$
Initial gap	$4\mu m$
density	$19300\raisebox{1ex}{$Kg$}\!\left/ \!\raisebox{-1ex}{$m^3$}\right.$

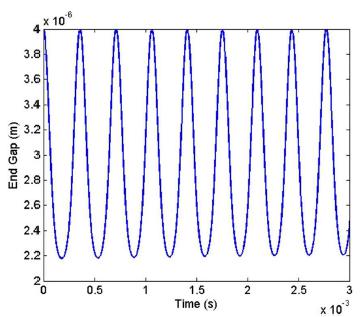
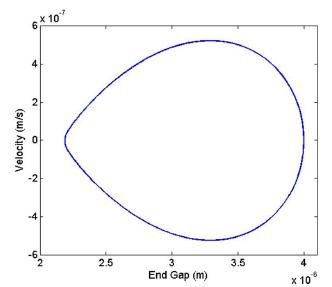
Variation of gap between end tip of micro beam and lower electrode versus to time (using couple stress theory) for applied voltage 10.44 V is depicted in Figure 3. As shown in this figure, with applying this voltage, micro beam oscillates and no instability occurs. Phase diagram relevant to this figure is shown in Figure 4. As shown in this figure, phase portrait of micro beam is a restricted oval-shaped environment, where asymmetry of this shape with respect to horizon axis is caused by nonlinear electrostatic force.

Figure 3:
End gap versus time under step DC voltage of $V_1=10.44V$actuation, using couple stress theory

Figure 4:
Velocity of end tip versus end gap under step DC voltage of $V_1=10.44V$ actuation, using couple stress theory

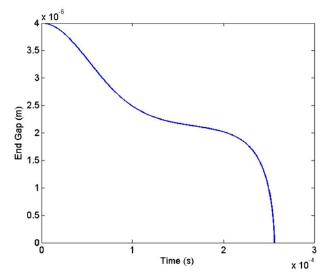
End gap versus time for applied voltage 10.45 is shown in Figure 5. As it can be observed in this figure, applying of 10.45V results in instability and collision of micro beam to lower electrode. Minimal applied voltage (10.45V) which causes the instability of micro beam, is entitled as dynamic instability voltage or dynamic pull-in voltage. Phase portrait of Figure 5 is shown in Figure 6. As shown in this figure increasing of end gap cause the tendency of velocity to higher values. These magnitude (pull-in voltage) was obtained by trial and error. If the applied voltage causes to instability (stability) of micro-switch the mentioned voltage decrease (increase) as long as obtaining dynamic pull-in voltage.

Figure 5:
End gap versus time under step DC voltage of $V_1=10.45V$ actuation, using couple stress theory

Figure 6:
Velocity of end tip versus end gap under step DC voltage of $V_1=10.45V$ actuation, using couple stress theory

Dynamic responses of micro beam to applied voltages 7.56V and 7.57V are drawn (using classic beam theory) and shown in Figure 7 and Figure 9 Related phase portraits are shown in Figure 8 and Figure 10 respectively. With comparing Figure 7 and Figure 9 it can be concluded that pull-in voltage of micro beam based on the classic beam theory is 7.57V. However, as mentioned before, using couple stress theory yields 10.45V for pull-in voltage. This remarkable difference between two magnitudes of pull-in voltage is because of considering and neglecting the effects of length scale parameter. Considering this effect, which causes the increase of bending rigidity of micro beam and consequently, the dynamic pull-in voltage is increased too.

Figure 7:
End gap versus time under step DC voltage of $V_1=7.56V$ actuation, using classic beam theory

Figure 8:
Velocity of end tip versus end gap under step DC voltage of ${\text{V}}_1=7.56\text{V}$ actuation, using classic beam theory

Figure 9:
End gap versus time under step DC voltage of $V_1=7.57V$ actuation, using classic beam theory

Figure 10:
Velocity of end tip versus end gap under step DC voltage of $V_1=7.57V$ actuation, using classic beam theory

Based on the reported results of ref [²]

${\left(V_{pull-in}\right)}_{classic}\propto \sqrt{\frac{E{h}^3{G}_0^3}{{\epsilon }_0{L}^4}}\propto \sqrt{\frac{EI{G}_0^3}{b{\epsilon }_0{L}^4}}$ (24)

Based on the couple stress theory and considering $EI+GA{L}^2$ as bending rigidity, the above equation may be presented as:

${\left(V_{pull-in}\right)}_{couple}\propto \sqrt{\frac{\left(EI+GA{L}^2\right)G_0^3}{b{\epsilon }_0{L}^4}}$ (25)

So following equation can be presented as ratio of pull-in voltage obtained using couple stress and classic beam theory:

$\frac{{\left(V_{pull-in}\right)}_{couple}}{{\left(V_{pull-in}\right)}_{classic}}=\sqrt{\frac{EI+GA{L}^2}{EI}}$ (26)

Based on the above relation mentioned ratio is about 1.381 for the studied micro-switch. As shown in Figure 6 and Figure 10 the ratio of pull-in voltages is $\frac{10.45}{7.57}=1.38$, where is conformable with Eq. (26).

Figure 11 shows phase portrait of micro beam subjected to various applied voltages (continuous and dashed curves related to couple stress and classic beam theories.). As can be observed in this figure for lower applied voltages, phase portraits are stable and full-symmetry. But with increasing applied voltage and in the proximity of pull-in voltage, phase diagram transmutes to asymmetric oval-shaped one. Phase portraits for applied voltages upper than pull-in one, are instable and increase of voltage results in increase of micro beam velocity. Comparing of voltages of coinciding diagram shows considerable difference between obtained magnitudes of applied voltage of two theories.

Figure 11:
Phase portrait of golden micro beam subjected various applied voltages

Variation of pull-in voltage versus micro beam length and initial gap are shown in Figure 12 and Figure 13 respectively. As can be seen in these figures pull-in voltage decreases with increase of length and decrease of initial gap. Although there are considerable differences between diagrams of couple stress and classic beam theories, these differences are more evident for low length and high gap. As can be seen in these figures for identical length or gap $\frac{{\left(V_{pull-in}\right)}_{couple}}{{\left(V_{pull-in}\right)}_{classic}}=1.38$. So ${\left(V_{pull-in}\right)}_{couple}-{\left(V_{pull-in}\right)}_{classic}\cong 0.38{\left(V_{pull-in}\right)}_{classic}$ and it is proved that difference of two obtained voltages is equal with $0.38{\left(V_{pull-in}\right)}_{classic}$ and with increase of ${\left(V_{pull-in}\right)}_{classic}$ this difference is increased too. As shown in Figure 12 and Figure 13 with increase of gap and decrease of length, ${\left(V_{pull-in}\right)}_{classic}$ is increased and by increasing of ${\left(V_{pull-in}\right)}_{classic}$, the difference of ${\left(V_{pull-in}\right)}_{couple}-{\left(V_{pull-in}\right)}_{classic}$ is increased too.

Figure 12:
Dynamic instable voltage versus length for golden micro beam

Figure 13:
Dynamic instable voltage versus primary gap for golden micro beam

In the following part of this section, the instability of micro switch with considering damping effects are investigated. Dynamic response of micro switch for applied voltages of 10.68V and 10.69V and $c=0.02$ is shown in Figure 14. As shown in this figure applying of 10.68V causes the oscillation of micro beam and as a consequence of damping effects, oscillation amplitude decreases gradually. But for applied voltage 10.65V micro beam loses its stability and collapses on to lower electrode. As shown in Figure 5 pull-in voltage for undamped case is 10.45V, but for the case with damping coefficient of $c=0.02$ is 10.69V, where it indicates increase of damping effect leads to the increase of pull-in voltage. Relevant phase diagram of Figure 14 is depicted in Figure 15. As shown in this figure phase diagram for applied voltage of 10.68 is spiral-shaped where with time elapsing, velocity tend to zero.

Figure14:
End gap versus time, for damping coefficient$c=0.02$, using couple stress theory

Figure 15:
Velocity of end tip versus end gap for damping coefficient $c=0.02$, using couple stress theory

Dynamic response and phase portraits of the micro beam subjected to applied voltages 7.79V and 7.8V for $c=0.02$ are depicted in Figure 16 and Figure 17. From Figure 16, it can be concluded that pull-in voltage based on the classic beam theory is 7.8V. As mentioned before, as a consequence of increase of damping effect, pull-in voltage increase too.

Figure 16:
End gap versus time, for damping coefficient $c=0.02$ , using classic beam theory

Figure 17:
Velocity of end tip versus end gap for damping coefficient $c=0.02$ , using classic beam theory

Variation of pull-in voltage versus damping coefficient was extracted and depicted in Figure 18 and Figure 19. As shown in these figures for c <1.8 pull in voltage depends on the damping ratio and with increasing this ratio the pull-in voltage increases too. But above this level (for c >1.8), pull-in voltage remains constant and can be regarded as damping-independent.

Figure 18:
variation of dynamic instable voltage versus damping coefficient using couple stress theory

Figure 19:
variation of dynamic instable voltage versus damping coefficient using classic beam theory

In the end of this section, dependency of pull-in time to damping coefficient is demonstrated. Pull-in diagram and pull-in voltage of micro switch considering various damping coefficient are drawn and shown in Figure 20 and Figure 21. It can be concluded from two figures, increase of damping coefficient results in the increase of pull-in time as well as pull-in voltage. The results of these figures are in good agreement with the results of ref. [⁴⁶].

Figure 20:
Instability diagrams of micro beam for various magnitude of damping coefficient, using couple stress theory

Figure 21:
Instability diagrams of micro beam for various magnitude of damping coefficient, using classic beam theory

6 CONCLUSION

Dynamic instability of three layer micro switch was studied using the classic beam and couple stress (with considering length scale parameter) theories. For this reason governing dynamic equation of micro switch was obtained with and without considering the length scale parameter. Considering the nonlinearity of governing equation, Galerkin method was implemented to solve the governing equation. The applied numerical method was validated with previous experimental and numerical methods. The validation results showed good ability of Galerkin method for solving the governing dynamic equation. Dynamic behavior and pull-in voltage of the micro switch were investigated with considering the damping effects and using two mentioned theories. The obtained results showed that the calculated pull-in voltage by couple stress theory is higher than the one calculated by classic beam theory. Also it was shown that the ratio of pull-in voltages based on the couple stress theory to classic beam theory is a specific value. Furthermore, the dependency of pull-in voltage to initial gap and micro-beam length were studied and it was shown that with increase of initial gap and decrease of micro-beam length, the effect of considering of length scale parameter gets more obvious. Obtained results indicate remarkable difference between results of classic beam and couple stress theories, where obtained pull-in voltage based on the couple stress theory is higher than the obtained one using classic beam theory. Moreover, the variation of pull-in voltage and pull-in time with respect to damping coefficient were investigated. Results of dynamic case with considering damping effects confirmed that with increasing damping coefficient, the amplitude of oscillation decreases. Acquired results in this case showed that increase of damping coefficient results in increase of pull-in voltage as well as pull-in time.

REFERENCES

• ^[1]
  W. Tian, Z. Chen, (2015), “Analysis of bistable inductive micro-switch based on surface micro size effect”, Applied Surface Science, 334(15), 32-39.
• ^[2]
  G. Rezazadeh, M. Fathalilou, M. Sadeghi, (2011), “Pull-in Voltage of Electrostatically-Actuated Microbeams in Terms of Lumped Model Pull-in Voltage Using Novel Design Corrective Coefficients”, Sens Imaging, 12, 117-131.
• ^[3]
  M. Taghizadeh, H. Mobki, (2014), “Bifurcation analysis of torsional micromirror actuated by electrostatic forces”, Archives of Mechanics, 66(2), 95-111.
• ^[4]
  Y. Wang, K. Kumar, L. Wang, X. Zhang, (2012), “Monolithic integration of binary-phase fresnel zone plate objectives on 2-axis scanning micromirrors for compact microscopes”, Optics express, 20(6), 6657-6668.
• ^[5]
  A. Koochi, H. Hosseini-Toudeshky, (2015), “Coupled effect of surface energy and size effect on the static and dynamic pull-in instability of narrow nano-switches”, International Journal of Applied Mechanics, 7(04), p.1550064.
• ^[6]
  A. Kanani, A. Koochi, M. Farahani, E. Rouhic, M. Abadyan, (2016), “Modeling the size dependent pull-in instability of cantilever nano-switch immersed in ionic liquid electrolytes using strain gradient theory”, Scientia Iranica. Transaction B, Mechanical Engineering, 23(3), 976-989.
• ^[7]
  M. Keivani, A. Koochi, M. Abadyan, (2017), “A New Bilayer Continuum Model Based on Gurtin-Murdoch and Consistent Couple-Stress Theories for Stability Analysis of Beam-Type Nanotweezers”, Journal of Mechanics, 33(2), 137-146.
• ^[8]
  J. Berthelot, S.S. Aćimović, M.L. Juan, M.P. Kreuzer, J. Renger, R. Quidant, (2014), “Three-dimensional manipulation with scanning near-field optical nanotweezers”, Nature nanotechnology, 9(4), 295-299.
• ^[9]
  H. Mobki, M. H. Sadeghia, G. Rezazadeh, (2015), “State Estimation of MEMs Capacitor Using Taylor Expansion”, International Journal of Engineering-Transactions B: Applications, 28(5), 764-770.
• ^[10]
  S. Afrang, H. Mobki, M.H. Sadeghi, G. Rezazadeh, (2015), “A new MEMS based variable capacitor with wide tunability, high linearity and low actuation voltage”, Microelectronics Journal, 46(2), 191-197.
• ^[11]
  H. Mobki, M. H. Sadeghi, G. Rezazadeh, (2015), “Design of Direct Exponential Observers for Fault Detection of Nonlinear MEMS Tunable Capacitor”, International Journal of Engineering-Transactions A: Basics, 28(4), 634-641.
• ^[12]
  A. G.P. Kottapalli, M. Asadnia, J. Miao, M. Triantafyllou, (2015), “Soft polymer membrane micro-sensor arrays inspired by the mechanosensory lateral line on the blind cavefish”, Journal of Intelligent material systems and structures, 26(1), 38-46.
• ^[13]
  N. Sugita, K. Ishii, T. Furusho, K. Harada, M. Mitsuishi, (2015), “Cutting temperature measurement by a micro-sensor array integrated on the rake face of a cutting tool”, CIRP Annals-Manufacturing Technology, 64(1), 77-80.
• ^[14]
  F. Tajaddodianfar, H.N. Pishkenari, M.R.H. Yazdi, E.M. Miandoab, (2015), “On the dynamics of bistable micro/nano resonators: analytical solution and nonlinear behaviour”, Communications in Nonlinear Science and Numerical Simulation, 20(3), 1078-1089.
• ^[15]
  J. F. Rhoads, S.W. Shaw, K.L. Turner, (2010), “Nonlinear dynamics and its applications in micro-and nanoresonators”, Journal of Dynamic Systems, Measurement, and Control, 132(3), 034001.
• ^[16]
  V. E. Demidov, S. Urazhdin, H. Ulrichs, V. Tiberkevich, A. Slavin, D. Baither, G. Schmitz, S.O. Demokritov, (2012), “Magnetic nano-oscillator driven by pure spin current”, Nature materials, 11(12), 1028-1031.
• ^[17]
  R.H. Liu, W.L. Lim, S. Urazhdin, (2013), “Spectral characteristics of the microwave emission by the spin Hall nano-oscillator”. Physical review letters, 110(14), 147601.
• ^[18]
  H. Mobki, M.H. Sadeghi, G. Rezazadeh, (2015), “Application of Thau observer for fault detection of micro parallel plate capacitor subjected to nonlinear electrostatic force” International Journal of Engineering, 28(2), 270-276.
• ^[19]
  Y.T. Beni, M. Abadyan, A. Koochi, (2011), “Effect of the Casimir attraction on the torsion/bending coupled instability of electrostatic nano-actuators”, Physica scripta, 84(6), 065801.
• ^[20]
  A. Koochi, A. Noghrehabadi, M. Abadyan, (2011), “Approximating the effect of van der Waals force on the instability of electrostatic nano-cantilevers”, International Journal of Modern Physics B, 25(29), 3965-3976.
• ^[21]
  H. Mobki, M.H. Sadeghi, S. Afrang, G. Rezazadeh, (2011), “On the tunability of a MEMS based variable capacitor with a novel structure”, Microsystem technologies, 17(9), 1447.
• ^[22]
  R. Soroush, A. L. I. Koochi, A.S. Kazemi, M. Abadyan, (2012), “Modeling the effect of Van Der Waals attraction on the instability of electrostatic cantilever and doubly-supported nano-beams using modified adomian method”, International Journal of Structural Stability and Dynamics, 12(05), 1250036.
• ^[23]
  A. Azizi, N.M. Fard, H. Mobki, A. Arbi, (2018), “Bifurcation Behaviour and Stability Analysis of a Nano-Beam Subjected to Electrostatic Pressure”, Applied and Computational Mathematics, 7(1-2), 1-11.
• ^[24]
  A. Koochi, N. Fazli, R. Rach, (2014), “Modeling the pull-in instability of the CNT-based probe/actuator under the Coulomb force and the van der Waals attraction” Latin American Journal of solids and structures, 11(8), 1315-1328.
• ^[25]
  N. Kacem, S. Baguet, S. Hentz, R. Dufour, (2011), “Computional and quasi-analytical models for non-linear vibrations of resonant MEMS and NEMS sensors”, International Journal of Non-Linear Mechanics, 46(3), 532-542.
• ^[26]
  J.G. Guo, L.J. Zhou, Y.P. Zhao, (2009), “Instability analysis of torsional MEMS/NEMS actuators under capillary force”, Journal of Colloid and Interface Science, 331(2), 458-462.
• ^[27]
  H.M. Sedighi, A. Koochi, M. Abadyan, (2014), “Modeling the size dependent static and dynamic pull-in instability of cantilever nanoactuator based on strain gradient theory”, International Journal of Applied Mechanics, 6(05), 1450055.
• ^[28]
  H. Mobki, M.H. Sadeghi, G. Rezazadeh, M. Fathalilou, (2014), “Nonlinear behavior of a nano-scale beam considering length scale-parameter” Applied Mathematical Modelling, 38(5), 1881-1895.
• ^[29]
  A. Koochi, H.M. Sedighi, M. Abadyan, (2014), “Modeling the size dependent pull-in instability of beam-type NEMS using strain gradient theory”. Latin American Journal of Solids and Structures, 11(10), 1806-1829.
• ^[30]
  K. Rashvand, G. Rezazadeh, H. Mobki, M.H. Ghayesh, (2013), “On the size-dependent behavior of a capacitive circular micro-plate considering the variable length-scale parameter”, International Journal of Mechanical Sciences, 77, 333-342.
• ^[31]
  K. Rashvand, G. Rezazadeh, H. Madinei, (2014), “Effect of length-scale parameter on pull-in voltage and natural frequency of a micro-plate” International Journal of Engineering, 27(3), 375-384.
• ^[32]
  K. Rashvand, G. Rezazadeh, R. Shabani, M. Sheikhlou, (2012), “On the size-dependent nonlinear behavior of a capacitive rectangular micro-plate considering modified couple stress theory”, In Proceedings of the 1st International Conference of Mechanical Engineering and Advanced Technology. ICMEAT Isfahan, Iran (pp. 10-12).
• ^[33]
  F.V. Tahami, H. Mobki, A.A.K. Janbahan, G. Rezazadeh, (2009), “Pull-in phenomena and dynamic response of a capacitive nano-beam switch”, Sensors & Transducers Journal, 110 (11), 26-37.
• ^[34]
  M. Dequesnes, S. V. Rotkin, N. R. Aluru, (2002), “Calculation of pull-in voltages for carbon nanotube-based nanoelectromechanical switches, Nanotechnology, 13, 120-131.
• ^[35]
  M. Dequesnes, Z. Tang, N.R. Aluru, (2004) “Static and Dynamic Analysis of Carbon Nanotube-based Switches”, journal of Engineering Materials and Technology, 126, 230-237
• ^[36]
  H. Mobki, G. Rezazadeh, M. Sadeghi, F. Vakili-Tahami, M-M. Seyyed-Fakhrabadi, (2013) “A comprehensive study of stability in an electro-statically actuated micro-beam”, International Journal of Non-Linear Mechanics, 48, 78-85.
• ^[37]
  A. Azizi, H. Mobki, G. Rezazadeh, (2016), “Bifurcation Behavior of a Capacitive Micro-Beam Suspended between Two Conductive Plates”, Int J Sens Netw Data Commun, 5(4), 1-10.
• ^[38]
  H. Mobki, K. Rashvand, S. Afrang, M. H. Sadegh, G. Rezazadeh, (2014) “Design, simulation and bifurcation analysis of a novel micromachined tunable capacitor with extended tunability” Transactions of the Canadian Society for Mechanical Engineering, 38 (1), 15-29.
• ^[39]
  H. Azimloo, G. Rezazadeh, and R. Shabani, (2015) “Development of a capacitive angular velocity sensor for the alarm and trip applications.” Measurement, 63, 282-286.
• ^[40]
  A. Shah-Mohammadi-Azar, H. Azimloo, G. Rezazadeh, R. Shabani, & B. Tousi, (2013). “On the modeling of a capacitive angular speed measurement sensor” Measurement, 46(10), 3976-3981.
• ^[41]
  F. Yang, A.C.M. Chong, D.C.C. Lam, P. Tong, (2002), “Couple stress based strain gradient theory for elasticity”, International Journal of Solids and Structures, 39(10), 2731-2743.
• ^[42]
  S.K. Park, X.L. Gao, (2006), “Bernoulli-Euler beam model based on a modified couple stress theory”, J. Micromech. Microeng., 16(11), 2355-2359.
• ^[43]
  H. Mobki, M. H. Sadeghi, G. Rezazadeh, M. Fathalilou, A-a. Keyvani-janbahan, (2014), “Nonlinear behavior of a nano-scale beam considering length scale-parameter”, Applied Mathematical Modelling, 38(5-6), 1881-1895.
• ^[44]
  E. S. Hung, S. D. Senturia, (1999), “Generating efficient dynamical models for microelectromechanical systems from a few finite-element simulation runs”, Journal of Microelectromechanical Systems, 8, 280-289.
• ^[45]
  M. Fathalilou, M. Sadeghi, G. Rezazadeh, M. Jalilpour, A. Naghilou, S. Ahouighazvin, (2011), “Study on the Pull-In Instability of Gold Micro-Switches Using Variable Length Scale Parameter”, Journal of Solid Mechanics, 3(2), 114-123.
• ^[46]
  G. Rezazadeh, F. Vakili-Tahami, H. Mobki, M. M. Seyyed Fakhrabadi, A. Alizadeh, (2010) “Static and Dynamic Pull-in Phenomena of a Capacitive Carbon Nano Tube”, 18th Annual International Conference on Mechanical Engineering-ISME 2010, Sharif University of Technology, Tehran, Iran, 11-13 May.

Publication Dates

• Publication in this collection
  2018

History

• Received
  31 Oct 2017
• Reviewed
  03 Nov 2017
• Accepted
  20 Mar 2018