A Backtracking Search Algorithm for the Simultaneous Size, Shape and Topology Optimization of Trusses

Abstract

This paper presents a Backtracking Search Optimization algorithm (BSA) to simultaneously optimize the size, shape and topology of truss structures. It focuses on the optimization of these three aspects since it is well known that the most effective scheme of truss optimization is achieved when they are simultaneously considered. The minimization of structural weight is the objective function, imposing displacement, stress, local buckling and/or kinematic stability constraints. The effectiveness of the BSA at solving this type of optimization problem is demonstrated by solving a series of benchmark problems comparing not only the best designs found, but also the statistics of 100 independent runs of the algorithm. The numerical analysis showed that the BSA provided promising results for the analyzed problems. Moreover, in several cases, it was also able to improve the statistics of the independent runs such as the mean and coefficient of variation values.

Keywords:
Backtracking Search algorithm; truss optimization; topology optimization; size optimization; shape optimization; mixed variable problem

1 INTRODUCTION

Optimization of trusses has been widely studied over the past decades, mostly because of the growing requirement from the industry for more economical design. In fact, several real life structures, or at least part of them, may be modelled using truss elements, such as roofs, towers, bridges, and so on. The difficulty of solving the optimization of truss structures may range from very simple problems to complex ones.

For example, a truss size optimization problem with continuous design variables and stress constraints is a linear and convex problem (considering a unique load case), which is rather simple to be solved. If shape variables are added to the problem, it becomes nonlinear and it may be nonconvex (Achtziger 2007, Torii et al. 2011, Torii et al. 2012). The difficulty of the problem may be further increased by including, for example, topology and discrete design variables. The latter usually comes from limitations of the manufacturing process, e.g. the available cross sectional areas in a manufacturer catalogue.

The so-called metaheuristic algorithms, are a class of optimization methods able to handle these difficulties, regarding the truss optimization problems. These algorithms can also be found in different applications, such as in Rojas et. al. (2012), Koide et. al. (2013), Lobato and Steffen Jr (2014), Behrooz et. al. (2016). Examples of these algorithms are the Genectic Algorithms (GA), Particle Swarm Optimization (PSO), Ant colony (AC) and others.

It is important to point out that lighter structures may be designed when the engineer considers the combined effect of size, shape and topology variables. However, most of the papers found in the literature regarding truss optimization using metaheuristics focused on one or two of these aspects. Indeed, metaheuristic algorithms have been extensively applied to the size optimization of trusses such as Goldberg and Samtani (1986), Adeli and Kamal (1991), and Rajeev and Krishnamoorthy (1992), Bland (2001), Lee et al. (2005), Kaveh and Talatahari (2009a), Kaveh and Talatahari (2009b), Sonmez (2011), Kazemzadeh Azad et al. (2014), Sadollaha et al. (2015), Kaveh and Mahdavi (2014), Kaveh et al. (2014), Degertekin (2012), Degertekin and Hayalioglu (2013), Zhanga et al. (2014), Hasançebi and Kazemzadeh Azad (2014), Kazemzadeh Azad and Hasançebi (2015a), Hasançebi and Kazemzadeh Azad (2015), Kazemzadeh Azad and Hasançebi (2014) to name just a few.

Papers regarding size and shape optimization can be found at Wu and Chow (1995), Salajegheh and Vanderplaats (1993), Galante (1996), Son and Yang (1996), Jármai et al. (2004), Agarwal and Raich (2006), Kelesoglu (2007), Miguel and Fadel Miguel (2012), Kaveh and Zolghadr (2014), Li (2014), among others.

However, when it comes to the simultaneous size, shape and topology optimization (SSTO) a limited number of papers is found, for example: Pereira et. al. (2004), Tand et al. (2005), Miguel et al. (2012), Miguel et al. (2013), Grierson and Pak (1993), Rajan (1995), Hajela and Lee (1995), Shrestha and Ghaboussi (1998), Deb and Gulati (2001), Ahari et al. (2014), Kaveh and Ahmadi (2014), Kutyłowski and Rasiak (2014), Gonçalves et al. (2015). This fact motivates the development of optimization methods and their application to the SSTO problem.

In this context, a Backtracking Search algorithm (BSA) (Civicioglu 2013. Miguel et al. 2015) is presented in this paper for the simultaneous SSTO of truss structures in the presence of discrete and continuous design variables. The selection of the BSA was mainly based on two aspects:

(a) it was shown to outperform several algorithms in unconstrained optimization (Civicioglu, 2013) and presented promising results for the optimization of transmission line towers structures, studied by Souza et al. (2016);

(b) it has only one parameter to be set, different from other metaheuristic algorithms. Indeed, one of the main drawbacks of metaheuristic algorithms is that their efficiency depends on the tuning of many parameters usually by trial and error (Lopez et al. 2009a, Lopez et al. 2009b).

This paper is organized as follows: in Section 2, the truss optimization problem is stated. In Section 3, the framework of the BSA is presented. Then, a set of benchmark problems regarding the SSTO of trusses is analyzed in Section 4, and finally Section 5 presents the main conclusions drawn from this work.

2 PROBLEM FORMULATION

The problem is formulated similarly to Miguel et al. (2013), where the topology is optimized through a ground structure concept, in which members and nodes are allowed to be eliminated in order to vary the truss topology.

Simultaneously, the algorithm performs the size optimization of the truss by changing the cross-sectional area (A ∊ R^m ) of the remaining structural members and the shape optimization by modifying the nodal coordinates of the nodes q modeled as design variables (ξ ∊ R^q' ). This optimization procedure searches for the minimum structural weight of the truss subjected to stress, displacement and kinematic stability constraints. For convenience of notation, the design variables A and ξ are grouped into the vector x =[A ₁,...,A_m , ξ ₁ ,..., ξ_q' ]. Thus, the optimization problem can be posed as:

(1)

Where n_v = m+q' which is the number of design variables of the optimization problem, W stands for the structural weight, m is the number of members in design, ρ is the specific weight of the bar material, l_j is the length of the j^th bar (which is represented by the nodal distances). σ_j is the stress of the j^th bar, while σ^t _j and σ^c _j are respectively the maximum allowable stress in tension and compression of the j^th bar; δ_k and δ ^max _k are the displacement and maximum allowable displacement of the k^th node, respectively. Ω is the discrete set comprised by n_p available cross sectional areas; A ^min _j and A ^max _j are the lower and upper bounds of the cross-sectional area of the j^th ar, respectively; and ξ^min _i and ξ^max _i are the lower and upper bounds of the allowable movement of the i^th nodal coordinate treated as design variable, respectively.

The displacement constraints (G2) are formulated by considering that the deflection in a specified coordinate direction of a node must be lower than an allowable displacement chosen by the designer. Likewise, the stress in the element must be lower than the allowable stress in tension and compression of the material (G3). However, if buckling constraints are included in the formulation, the allowable stress in compression is the lowest value between the maximum stress in compression of the material and the critical stress given by the Euler's equation (see Eq.(5) in section 5.3). Finally, kinematic stability (G1) is achieved by checking the positive definiteness of the stiffness matrix of each solution, by evaluating the determinant of the stiffness matrix, i.e. computationally, it should be higher than a very small number, e.g.10^-7. If it is not, a penalization of 10²⁰ is applied to this solution. Thus, an unstable design is not analyzed and the constraints according to stress and/or displacement are not evaluated. It is important to highlight that every individual generated by the algorithm is counted as an objective function evaluation, even when the truss analyses is not performed (unstable topologies).

If the stability constraint is satisfied, the member forces and node displacements are calculated. Then, if one or more of the displacement and/or stress constraints are violated (constraints G2 and G3 in Eq. (1)), a penalty P_t is added to the objective function value of the current design. In this case, the penalty magnitude is proportional to the violation, and takes the form:

(2)

in which h is a positive parameter defined according to de characteristics and magnitude of each example, i is equal to t if the member is in tension and i is equal to c if the member is in compression. Finally, constraints on the allowable cross sectional areas and node positions are addressed by a coding approach. These bounds are imposed by not sampling infeasible designs in the computer code. Thus, the resulting optimization problem to be solved by the BSA is: stands for the absolute value,

(3)

3 BACKTRACKING SEARCH ALGORITM (BSA)

The BSA is multi-agent based evolutionary algorithm developed by Civicioglu (2013) able to solve unconstrained non-convex optimization problems. It is thus employed in this paper to address the optimization problem given by Eq. 3.

An overview of the algorithm is presented in Figure 1. In the initialization step, the initial population of BSA is randomly generated. Then, the population is perturbed, using the "direction/length" of the perturbation; the parameter (m_r ); the scale factor α and the matrix M. Because of the perturbation process, some variables may extrapolate the boundaries of the design domain; in this case, these variables are randomly regenerated. In the final step, the fitness values are evaluated in order to select the new population. The process is repeated until the stop criteria is met.

Figure 1:
Pseudocode of BSA.

For a more detailed description of the BSA, the reader is referred to Civicioglu (2013) and Souza et al. (2016)

In the original description of the BSA, the author claimed that this algorithm had only one parameter to be adjusted, the mix rate (m_r ). It was only possible to have this one parameter due to the following aspects: (i) fixing the probability of occurrence of cases 1 and 2 in the construction of both P_old and M, and (ii) fixing the length of the perturbation, i.e. the value of α. Of course, these parameters may also be adjusted accordingly to the designer needs. In fact, on this paper the mix rate (m_r ) was kept unchanged from the original version of BSA, while the scale factor α, was the parameter adjusted, based on its performance on each studied example.

4 BSA FOR SIMULTANEOUS TOPOLOGY, SHAPE AND SIZE OPTIMIZATION

The BSA was originally proposed for unconstrained continuous optimization problems. Thus, in order to apply it to a constrained and discrete problem, some modifications are necessary.

The constraints can be divided into two categories: the first one (G1, G2, and G3) regards the structural behavior (Section 2) and the second one (G4 and G5) regards the range of the design variables (Section 2). The former is addressed by the algorithm through a penalization strategy described by Eq. 2 and Eq. 3 of the Section 2. The scheme allows the optimization process to avoid undesirable parts of the domain, penalizing each design proportionally to its violation. The latter is addressed by setting upper and lower bounds to the range of the variables, which will be used by the BSA. Thus, the range is applied on the "Initialization" phase and also at the end of the "Construction of the trial or perturbed population P_pert . Hence, the constrained optimization problem can be transformed in an unconstrained optimization problem.

In order to deal with discrete variables, an operator is employed at the very beginning of the structural analysis code. In this step, the continuous values generated by the BSA are rounded into discrete ones. For instance, in the size optimization, the continuous variables can be rounded into each 1.0 in ² or, still, into an integer value which corresponds to a value on a discrete set of cross-sectional areas. Then, the BSA only deals with continuous variables. It is important to highlight that this strategy does not demand any modifications on the BSA itself since the operator is applied within the structural analysis code.

Furthermore, this strategy it is easily applicable to any other optimization algorithms originally developed for unconstrained continuous problems. The approach employed on this paper has been successfully applied by other researches, such as Miguel and Fadel Miguel (2012), Miguel et al. (2013) and Gonçalves et al. (2015).

In order to address the simultaneous optimization of size, shape and topology of trusses, a single-stage procedure is performed, in which all variables including topology, shape and size are determined simultaneously. Here, we employed different approaches for eliminating members when the cross-section areas are continuous or discrete. These approaches are detailed in the following.

In the case of continuous cross-sectional areas, during the optimization process, a specific member is eliminated from the ground structure following the criteria proposed by Deb and Gulati (2001). The cross-sectional area of a member is compared to a specific critical cross-sectional area. If the member area is smaller than this specific value, this element is eliminated from the ground structure. This method defines how different topologies can be obtained in a continuous optimization procedure. Note that the critical cross-sectional area and the lower (A ^min) and upper (A ^max) bounds of the cross-sectional areas must be determined by considering the probability of a specific element to be absent from the final solution. For example, if A ^min = -A ^max and the critical cross-sectional area is zero, the probability of any member being present in the final structure is approximately 50 %.

In the case of discrete cross-sectional areas, the user defines the number of zeros that are added to the available profile set Ω, where a member addressed to a zero cross-sectional area, is eliminated from the ground structure. As well as the values of A ^min, A ^max and the critical area for the continuous case, the number of zeros added to the set Ω is defined in order to generate a reasonable probability of eliminating an element from the ground structure. It is important to highlight that the supports and nodes carrying loads cannot be disregarded in the final solution.

Finally, the results presented on the following Tables and Figures are feasible solutions (i.e. a solution that respects all the imposed constraints) achieved by the optimization algorithm. The results are compared regarding the weight of the best design, mean value and coefficient of variation of the 100 independent runs. The additional information about the best designs (found by the present study and the ones reported in the literature) are presented in the ^{Appendix A}.

4.1 Eleven-Bar Truss Example

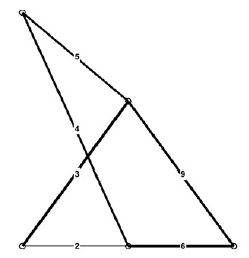
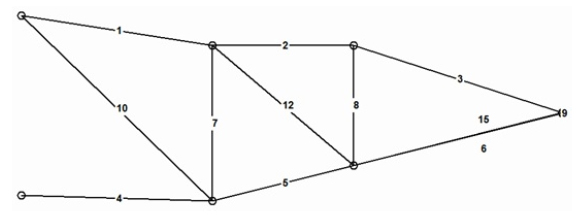
This truss has been extensively used as a benchmark problem and appears in several papers on truss optimization. The ground structure for this example is shown in Figure 2 and the design parameters are given in Table 1. Here, we perform the simultaneous SSTO of this structure.

Table 1:
Design parameters for the eleven-bar truss problem.

Design parameter	Value
Modulus of elasticity	68947.591 MPa
Weight density	2767.990 kg/m3
Allowable stress in tension	172.396 MPa
Allowable stress in compression	172.396 MPa
Allowable y-displacement	50.8 mm

Figure 2:
Eleven-bar truss benchmark example.

This problem was studied by Rajan (1995) and Balling et al. (2006) who employed the GA, Martini (2011) who employed the Harmony Search (HS), and Miguel et al. (2013) who employed the FA. In this study, the truss shape is optimized allowing the vertical coordinates of the three superior nodes (1, 2 and 3, Figure 2) to move between 457.2 cm and 2540 cm. The cross-sectional areas, for each of the 11 bars, come from the discrete set Ω = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10.45159, 11.61288, 15.35481, 16.90319, 18.58061, 19.93544, 20.19351, 1.80641, 23.41931, 24.77414, 24.96769, 26.96769, 28.96768, 30.96768, 32.06445, 33.03219, 37.03218, 46.58055, 51.41925, 74.19340, 87.09660, 89.67724, 91.61272, 99.99980, 103.22560, 121.29008, 128.38684, 141.93520, 147.74164, 170.96740, 193.54800, 216.12860)cm ². Thus, the design vector can be written as x = [A ₁ , A ₂ ,...A ₁₁ , ξ ₁, ξ ₂, ξ ₃]. Note that the first 10 cross-section areas from the set Ω are null values. Where a member addressed to a null area is eliminated from the structure.

Because the nodal coordinates are continuous variables and the cross-sectional areas are taken from a set of 42 discrete variables, the problem is a mixed variable optimization problem in that it simultaneously addresses discrete and continuous design variables.

In this example, the stopping criterion for each search was set as the number of objective function evaluations, i.e. OFE = 50000, to compare the results obtained here to the ones of Miguel et al. (2013), which found the best design in the literature and provided statistics for a series of runs of the FA.

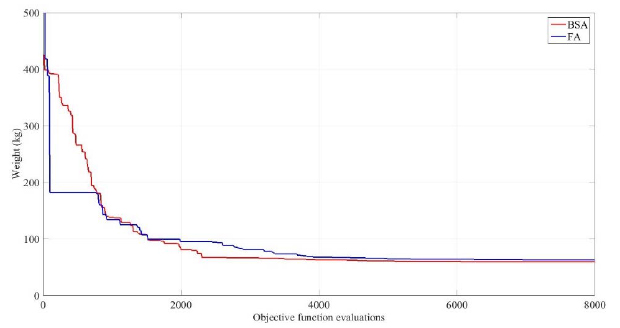
The parameters in this example were set as n_pop = 10, it _max = 5000, the penalization term h was set as 10⁸ and the scale factor α was set as 3 randn, where randn is random number from a standard normal distribution between 0 and 1. The results obtained by the BSA are presented in Table 2 and compared to the results of other algorithms taken from the literature. Figures 3 illustrates the topology of the optimized structure. Figure 4 showsthe converge curve of the best result found with BSA and FA (Miguel et al. 2013), one can notice that despite the similar results, the BSA converged significantly faster.

Table 2:
Results for the size, shape and topology optimization of the eleven-bar truss.

Resul	Rajan (1995)	Balling et. al. (2006)	Martini (2011)	Miguel et. al. (2013)	Present study
OFE	3840	500000	4075	50000	50000
Weight (kg)	1475.999	1241.029	1315.418	1227.04	1227.070
Mean weight	-	-	-	1268.285	1265.654
C.O.V. (%)	-	-	-	2.12	2.02

Figure 3:
Optimized configuration for the size, shape and topology optimization problem of the eleven-bar.

Figure 4:
Convergence curves for the size, shape and topology optimization of the eleven-bar truss.

The best result over 100 runs in this study weights 1227.070 kg, which is slightly worse than the value found by Miguel et al. (2013) (1227.040 kg), but better than the optimum weight determined by Balling et al. (2006) (1241.029 kg), Rajan (1995) (1475.999 kg) and Martini (2011) (1315.418 kg). The mean value and COV provided by the BSA are equal to 1265.654 kg and 2.02%, respectively, which are better than the ones found by the FA of Miguel et al. (2013) (1268.285 kg and 2.12%, respectively). Thus, the proposed scheme improved the mean and COV results than the cited references.

4.2 Thirty-Nine-Bar Two-Tiered Truss Example

The second benchmark example is the single-span 39-bar, 12-node, simply supported, two-tiered ground structure shown in Figure 5. This structure was studied before by Deb and Gulati (2001), Luh and Lin (2008), Wu and Tseng (2010), Lu and Lin (2011), Miguel et al. (2013) and Ahrari et al. (2014).

Figure 5:
Two-tiered truss, thirty-nine-member benchmark example (Miguel et al 2013).

Two independent studies are performed: (i) size and topology optimization and (ii) simultaneous SSTO. However, the cross-sectional areas are treated as continuous variables in this case to properly compare the results to those of the literature. The overlapping members are shown laterally dislocated in the figure for visual clarity. Because the vertical symmetry around member 19 is assumed, the number of variables is reduced to 21. The allowable strength is 137.895 MPa; the material properties and maximum allowable deflection are the same as those in the previous problem. The stopping criterion is set to OFE = 50000. The BSA parameters employed in both cases were n_pop = 20 and it _max = 2500, the penalization term h was set as 10⁸, and the scale factor α was set as 1/gamrnd(1,0.5), where gamrnd(1,0.5) is a random number from a gamma distribution with shape parameter 1 and scale parameter 0.5.

4.2.1 Size and Topology Optimization

The procedure for this example consists of the optimization of 21 continuous variables. Each size variable is allowed to vary between -1.4516∙10-⁴ and 1.45161∙10^-3, (in square meters). Where, for values below 3.2258∙10^-5, the respective member is eliminated from the ground structure. The design vector can be written x = [A ₁ , A ₂ ,...A ₂₁]. The results found by this study, and others provided by the literature, for this example are listed in Table 3. Figure 6 shows the topology of the best solution given by the BSA, which contains 10 nodes and 18 members. The convergence curves of the BSA and the FA (from Miguel et al. 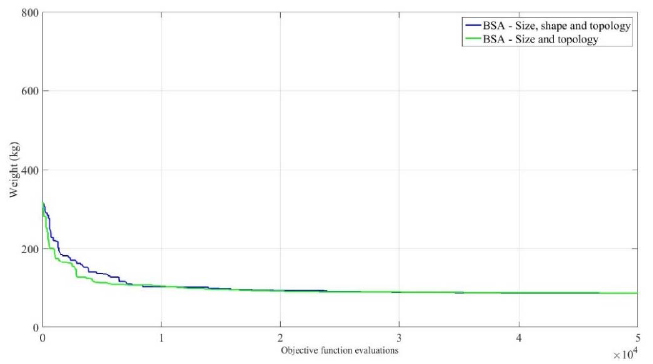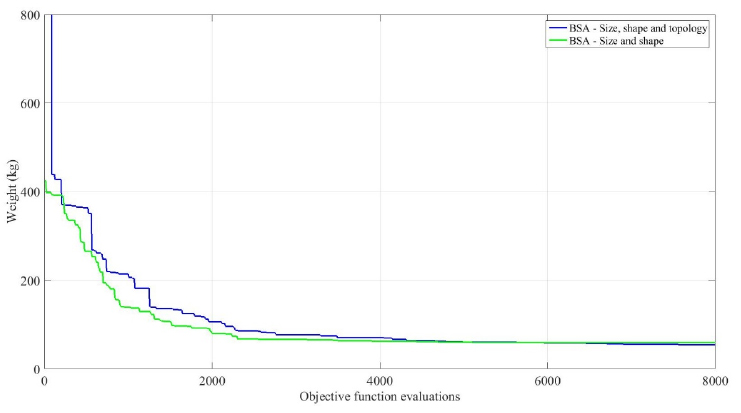2013) for this problem are shown in Figure 7.

Table 3:
Results for the size and topology optimization of the eleven-bar truss.

Result	Deb and Gulati (2001)	Luh and Lin (2008)	Wu and Tseng (2010)	Lu and Lin (2011)	Miguel et. al. (2013)	Present study
OFE	504000	303600	32300	262500	50000	50000
Weight (kg)	89.152	87.758	87.634	87.549	87.792	87.637
Mean weight (kg)	-	-	-	-	100.552	93.284
C.O.V. (%)	-	-	-	-	12.9	5.28

Figure 6:
Optimized configuration for the size and topology optimization of the thirty-nine-member truss.

Figure 7:
Convergence curves for the size and topology optimization of the thirty-nine-member truss.

The best result over 100 runs weights 87.637 kg, which is slightly heavier than the 87.549 kg found by Lu and Lin (2011). The mean value obtained using the BSA is equal to 93.284 kg and the coefficient of variation is 5.28%. The coefficient of variation and mean value are only compared with Miguel et al. 2013, since the other studies do not provide this information.

4.2.2 Size, Shape and Topology Optimization

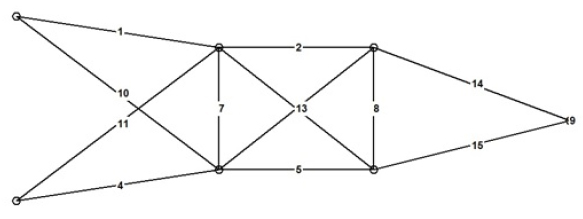
To carry out simultaneous SSTO, selected nodal coordinates are taken as design variables in addition to the 21 cross sectional areas. Assuming symmetry and considering that constrained and load-carrying nodes must remain fixed, and the highest node at the center of the structure does not move laterally, it is possible to reduce the number of nodal coordinates to 7. Each of these 7 nodes is allowed to move (-304.8, 304.8) cm from its original position (Figure 5). The design vector can then be written as: x = [A ₁ , A ₂ ,...A ₂₁ , ξ ₁, ξ ₂, ξ₇ ].

Figure 8 illustrates the topology of the best design found by the BSA over the 100 runs. Note that this topology contains 11 nodes and 20 members. Figure 9 presents the results reached by the present study and others found in the literature are listed in Table 4. The best result over 100 runs achieved by the BSA weights 86.753 kg, which is slightly lighter than the one found by Miguel et al. (2013), but heavier in comparison to the result presented by Ahrari et al. (2014), which is 82.091 kg. The mean value and COV achieved by the BSA optimization scheme are equal to 100.590 kg and 4.60%, respectively, while the ones of the FA are 94.478 kg and 5.3%, respectively. Hence, in this example, the BSA was able to improve the COV.

Figure 8:
Optimized configuration for the SSTO of the thirty-nine-member truss.

Figure 9:
Convergence curves for the size, shape and topology optimization of the thirty-nine-member truss.

Table 4:
Results for the size, shape and topology optimization of the thirty-nine-member truss.

Result	Deb and Gulati (2001)	Luh and Lin (2008)	Wu and Tseng (2010)	Lu and Lin (2011)	Miguel et. al. (2013)	Ahrari, Atai, and Deb (2014)	Present study
OFE	504000	453600	137200	262500	50000	40256	50000
Weight (kg)	87.176	85.607	85.469	85.541	86.774	82.091	86.753
Mean weight	-	-	-	-	94.478	-	100.59
C.O.V. (%)	-	-	-	-	5.3	-	4.6

Figure 9 shows the convergence curves for the best results found with the BSA and FA (from Miguel et al. 2013), similarly to previous examples the BSA converged faster, in comparison to the FA. Furthermore, in Figure 10 is shown the convergence curves for the cases 4.2.1 and 4.2.2. Where the better convergence in the earlier iterations for the size and topology case can be associated to the increase of possibilities provided by the geometrical variations allowed in case 4.2.2.

Figure 10:
Convergence curves for the size and topology and size, shape and topology optimization of the thirty-nine-member truss.

4.3 Fifteen-Bar Planar Truss Example

This fifteen-bar planar truss was studied by Wu and Chow (1995), Tang et al. (2005), Rahami et al. (2008), Miguel et al. (2013) and Gholaizadeh (2013). The ground structure is illustrated in Figure 11, showing a vertical tip load P = 44482.2161 N applied on node 8. The allowable strength of the material is 172.369 MPa for both tension and compression, and the material properties (modulus of elasticity and weight density) are the same as in the previous examples. The x and y coordinates of nodes 2, 3, 6 and 7 and the y-coordinate of the nodes on bar9 are taken as design variables. However, nodes 6 and 7 are constrained to have the same xcoordinates of the nodes 2 and 3, respectively. Thus, the problem includes fifteen size and eight shape variables (x2=x6, x3=x7, y2, y3, y4, y6, y7, y8).

Figure 11:
Fifteen-bar planar truss benchmark example.

The cross-sectional areas are chosen from the set Ω = (0.716, 0.910, 1.123, 1.419, 1.742, 1.852, 2.239, 839, 3.477, 6.155, 6.974, 7.5748.600, 9.600, 11.381, 13.819, 17.400,18.064, 20.200, 23.000, 24.600, 1.000, 38.400, 42.400, 46.400, 55.000, 60.000, 70.000, 86.000, 92.193, 110.774, 123.742) cm². The side constraints for the shape variables are 254 cm ≤ x2 ≤ 355.6 cm, 558.8 cm ≤ x3 ≤ 660.4 cm, 254 cm ≤ y2 ≤ 355.6 cm, 254 cm ≤ y3 ≤ 355.6 cm, 127 cm ≤ y4 ≤ 228.6 cm, -50.8 cm ≤ y6 ≤ 50.8 cm, -50.8 cm ≤ y7 ≤ 50.8 cm, and 50.8 cm ≤ y8 ≤ 50.8 cm.

Two independent studies are performed: (i) size and shape optimization, (ii) simultaneous SSTO. On both cases buckling constraints are considered.

For all examples the design vector can be written as x = [A ₁ , A ₂ ,...A ₁₅ , ξ ₁, ξ ₂, ξ₈ ]. In order to perform the topology optimization10 null cross-sectional areas are added to the available set Ω. If a size variable A_j assumes a null value, the respective member is eliminated from the structure.

The BSA parameters were set in these two studies as n_pop = 8 and it _max = 1000, resulting in 8000 OFE. The penalization term was set as 10⁸ and the scale factor α was set as 1/gamrnd(1,0.5).

The member stresses are constrained to be below the Euler buckling stress, as shown in Eq. 4:

(4)

4.3.1 Size and Shape Optimization with Buckling Constraints

Wu and Chow (1995) and Miguel et al. (2013) have studied this problem using the GA and FA, respectively.

Wu and Chow (1995) carried out the optimization using a population of 30 individuals. However, they did not mention the maximum number of generations. Miguel et al. (2013) employed 10 fireflies and 800 iterations, resulting in 8000 OFE.

The BSA results together with a comparison with the GA and FA are presented in Table 5. The best design found by the BSA is illustrated in Figure 12. Figure 13 shows the convergence curves of the best results found with the BSA and FA (from Miguel et al. (2013)).

Table 5:
Results for the size and shape optimization with buckling constraint of the 15-bar truss.

Result	Wu and Chow (1995)	Miguel et. al. (2013)	Present study
	GA	FA	BSA
OFE	-	8000	8000
Weight (kg)	182.506	62.627	59.641
Mean weight	-	69.948	64.049
C.O.V. (%)	-	3.85	3.96

Figure 12:
Optimized configuration for the size and shape optimization with buckling constraint of the 15-bar truss.

Figure 13:
Convergence curves for the best result for the size and shape optimization with buckling constraint of the 15-barr truss.

The best results over 100 runs achieved by the BSA weights 59.641 kg, which is lighter than the ones of the GA and FA. The mean value and COV reached by the BSA are equal to 64.049 kg and 3.96%, respectively. Thus, on the one hand, the BSA reduced the mean value of the independent runs in 9.21%, and on the other hand, the COV was around 2.7% higher than the one of the FA.

4.3.2 Size, Shape and Topology Optimization with Buckling Constraints

As proposed by Miguel et al. (2013), in addition to the eight discrete size and five continuous configuration variables, all fifteen member groups are considered as topology variables in this example. In order to employ the topology optimization, simultaneously to the size and shape optimization, 10 null areas are added to the set of possible cross-sectional areas. Thus, when a null area is addressed, the respective member is eliminated from the structure.

The results of the BSA and FA are presented in Table 6, while the topology of the best design is illustrated in Figure 14. Figure 15 shows the convergence curves of the best results found with the BSA and FA (from Miguel et al. (2013)), one can notice that the BSA presented a faster convergence in comparison to the FA. Furthermore, Figure 16 presents the converge curves for cases 4.3.1 and 4.3.2, where it is possible to obverse that the increase of possible solutions (provided by the topology variations allowed) delayed the convergence of the algorithm, however achieve a better result.

Table 6:
Results for the size, shape and topology optimization with buckling constraint of the 15-bar truss.

Result	Miguel et. al. (2013)	Present study
OFE	8000	8000
Weight (kg)	56.803	54.827
Mean weight	69.223	60.187
C.O.V. (%)	8.69	7.88

Figure 14:
Optimized configuration for the size, shape and topology optimization with buckling constraint of the 15-bar truss.

Figure 15:
Convergence curves for the best result for the size, shape and topology optimization with buckling constraint of the 15-bar truss.

Figure 16:
Convergence curve for the best result for the size and shape and size, shape and topology optimization with buckling constraint of the 15-bar truss.

The best design over 100 runs achieved by the BSA weights 54.418 kg, which is 3.48% lighter than the best design provided by the FA. The mean value and COV reached in the present study are equal to 60.187 kg and 7.88%, respectively. Thus, the BSA reduced the mean value by 13.05% and the COV by 0.81%, when compared to the FA. The results for this case show that the BSA was capable of not only provide the lightest design ever found for this problem, but also lower mean and COV values.

4.4 Twenty-Five-Bar 3D Truss Example

This example was studied before by Rajeev and Krishnamoorthy (1992), Wu and Chow (1995), Tang et al. (2005),Rahami et al. (2008), Miguel et al. (2013), Gholaized (2013) and Ahrari Atai and Deb (2014).The ground structure is shown in Figure 17. The mechanical properties and the loading conditions are presented in Table 7, while the nodes coordinates and member grouping are presented in Table 8. The structure is subject to a stress constraint of 275.8 MPa for each member, and a displacement constraint of 0.89 cm for each node.

Figure 17:
Twenty-five-bar 3D truss example.

Table 7:
Mechanical properties and loading conditions for the twenty-five-bar 3D truss example.

Mechanical properties
Modulus of elasticity	E=68.95 GPa
Density of the material	ρ=0.0272N/cm3
Loading (Node)	Fx (kN)	Fy (kN)	Fz (kN)
1	4.454	-44.482	-44.482
2	0	-44.482	-44.482
3	2.224	0	0
6	2.669	0	0

Table 8:
Nodes coordinates and member grouping for the twenty-five-bar 3D truss example.

Node	X(cm)	Y(cm)	Z(cm)	Group	Member (end nodes)
1	-95.25	0	508	A1	1(1,2)
2	95.25	0	508	A2	2(1,4), 3(2,3), 4(1,5). 5(2,6)
3	-95.25	95.25	254	A3	6(2,5), 7(2,4), 8(1,3), 9(1,6)
4	95.25	95.25	254	A4	10(3,6), 11(4,5)
5	95.25	-95.25	254	A5	12(3,4), 13(5,6)
6	-95.25	-95.25	254	A6	14 (3,10), 15(6,7), 16(4,9), 17(5,8)
7	-254	254	0	A7	18(3,8), 19(4,7), 20(6,9), 21(5,10)
8	254	254	0	A8	22(3,7), 23(4,8), 24(5,9), 25*6,10)
9	254	-254	0
10	-254	-254	0

During the optimization the cross-sectional areas are chosen from the set Ω = (0.645, 1.290, 1.936, 2.581, 3.226, 3.871, 4.512, 5.161, 5.807, 6.452, 7.097, 7.742, 8.387, 9.032, 9.677, 10.323, 10.968, 11.613, 12.258, 12.903, 13.548, 14.193, 14.839, 15.484, 16.129, 16.774, 18.065, 19.355, 21.935) cm².

Two independent studies were performed: (i) size and shape optimization and (ii) simultaneous size, shape and topology optimization.

The BSA parameters were set in these two studies as n_pop = 10 and it _max = 600, resulting in 6000 OFE. The penalization term was set as 10⁸ and the scale factor α was set as 4·randg, where randg is a scalar random value chosen from a gamma distribution with unit scale and shape. The statistical results presented, for both cases, are extracted from 100 independent runs of the algorithm.

4.4.1 Size and Shape Optimization

For the size variation, the member groups are allowed to assume the cross-sectional areas from the set Ω. The x, y, and z coordinates of nodes 3, 4, 5 and 6 and the x and y coordinates of nodes 7-10 are taken as design variables, while nodes 1 and 2 remains unchanged. Due to symmetry of the structure there are five shape variables, with the following bounds: 50.8 cm ≤ x₄≤ 152.4 cm, 101.6 cm ≤ x₈≤ 203.2 cm, 101.6 cm ≤ y₄≤ 203.2 cm, 254 cm ≤ y₈≤ 355.6 cm and 228.6 cm ≤ z₄≤ 330.2 cm. Thus, the design vector can be written as x = [A ₁ , A ₂ ,...A ₈ , ξ ₁, ξ ₂,... ξ ₅].

The results for this case are presented in Table 9, the best result found with the BSA was 54.02 kg, which slightly worse compared to Miguel et al. (2013) and Gholaized (2013). Figure 18 presents the convergence curves for the BSA and FA and Figure 19 illustrates the best design found with BSA.

Table 9:
Results for the size and shape optimization of the Twenty-five-bar 3D truss example.

Result	Rajeev and Krishnamoorthy (1992)	Wu and Chow (1995)	Tang et al. (2005)	Miguel et al. 2013	Gholaizedh (2013)	Present study
OFE			6000	6000	8000	6000
Weight (kg)	247.6658	61.7792	56.6718	53.9003	53.1746	54.0189
Mean weight (kg)				60.010		61.8256
C.O.V. (%)				5.5		5.55

Figure 18:
Convergence curves for the size and shape optimization of the twenty-five-bar 3D truss example.

Figure 19:
Optimized configuration for the size and shape optimization of the twenty-five-bar 3D truss example.

4.4.1 Size, Shape and Topology Optimization

In order to perform the topology variation each one of the eight member groups are allowed to be eliminated during the optimization process. To do so, 20 null areas are added to the set of possible cross-sectional areas Ω.

The results for this case are shown in Table 10, the BSA presented a lower C.O.V compared with the FA, however the best result (53.94 kg) and mean weight (66.84 kg) were worst compared to previous works. The configuration of the best result found with the BSA and the convergence curves of the BSA and FA are presented in Figures 20 and 21, respectively. Additionally, Figure 22 presents the convergences curves for the size and shape and size, shape and topology optimization cases. Similarly to the previous examples, the BSA presented a faster convergence in the early iterations.

Table 10:
Results for the size, shape and topology optimization of the Twenty-five-bar 3D truss example.

Result	Rajeev and Krishnamoorthy (1992)	Wu and Chow (1995)	Tang et al. (2005)	Miguel et al. 2013	Gholaizedh (2013)	Present study
OFE		6000	6000	8660	10000	6000
Weight (kg)	61.7792	53.8550	52.8798	51.8986	51.8728	53.9444
Mean weight (kg)			63.1219			66.8429
C.O.V. (%)			8			6.96

Figure 20:
Optimized configuration for the size, shape and topology optimization of the twenty-five-bar 3D truss example.

Figure 21:
Convergence curves for the size and shape optimization of the twenty-five-bar 3D truss example.

Figure 22:
Convergence curve for the best result for the size and shape and size, shape and topology optimization of the twenty-five-bar 3D truss example

5 CONCLUDING REMARKS

This paper presented a Backtracking Search Algorithm (BSA) for the simultaneous SSTO of truss structures. It focused on the optimization of these three aspects since it is well known that the most effective scheme of truss optimization is when one considers them simultaneously. In addition, in most of the examples, we deal concurrently with continuous and discrete design variables, due to the difficulties that they impose.

The effectiveness and robustness of the algorithm were demonstrated through a series of benchmark problems taken from the literature. Not only the best design obtained by each algorithm was compared, but also the statistics of the best designs found over 100 independent runs of the BSA. This statistical analysis is of paramount importance due to the stochastic nature of metaheuristic algorithms. Hence, the results presented here may serve as a more formal basis of comparison for future researchers analyzing the same problems with other optimization methods.

From the numerical analysis, it was shown that the BSA provided the best design ever found for several of the analyzed problems. Moreover, in some cases, it was also able to improve the statistics of the independent runs such as the mean and COV values. These results emphasize the capabilities of the BSA in this field and motivate its further development as well its application to real engineering problems.

Acknowledgements

The authors gratefully acknowledge the financial support of CNPq and CAPES.

References

• Achtziger, W. (2007). On simultaneous optimization of truss geometry and topology. Structural and Multidisciplinary Optimization 33: 285-305. DOI 10.1007/s00158-006-0092-0
  » https://doi.org/10.1007/s00158-006-0092-0
• Adeli, H., Kamal, O. (1991). Efficient optimization of plane trusses. Adv. Eng Softw. 13(3): 116-122.
• Agarwal, P and Raich, A.M. Design and optimization of steel trusses using genetic algorithms, parallel computing, and human-computer interaction Structural Engineering and Mechanics.23(4): 325-337.
• Ahrari, A., Atai, A.A., Deb, K. (2014). Simultaneous topology, shape and size optimization of truss structures by fully stressed design based on evolution strategy. Eng. Optimiz. DOI:10.1080/0305215X.2014.947972
  » https://doi.org/10.1080/0305215X.2014.947972
• Balling, R.J., Briggs, R.R., Gillman, K. (2006). Multiple optimum size/shape/topology designs for skeletal structures using a genetic algorithm., J Struct. Eng. 132(7): 1158-1165. DOI:10.1061/ ASCE0733-9445 2006132:7 1158
• Behrooz, A., Mohammad, R. K. R., Shahram Y., Mahdi T. (2016) A heuristic algorithm based on line-up competition and gener-alized pattern search for solving integer and mixed integer non-linear optimization problems. Latin American Journal of Solids and Structures. 13(2).
• Bland, J.A. (2001). Optimal structural design by ant colony optimization. Eng Optimiz. 33(4): 425-443. DOI:10.1080/03052150108940927
  » https://doi.org/10.1080/03052150108940927
• Civicioglu, P. (2013). Backtracking search optimization Algorithm for numerical optimization problems. Appl. Math. Comp. 219:8121-8144. DOI: 10.1016/j.amc.2013.02.017.
  » https://doi.org/10.1016/j.amc.2013.02.017
• Deb, K., Gulati, S. (2001). Design of truss-structures for minimum weight using genetic algorithms. Finite Elem. Anal. Des. 37: 447-465.
• Degertekin, S.O. (2012). Improved harmony search algorithms for sizing optimization of truss structures. Comput. Struct. (92-93): 229-241. DOI: 10.1016/j.compstruc.2011.10.022.
  » https://doi.org/10.1016/j.compstruc.2011.10.022
• Degertekin, S.O. and Hayalioglu, M.S. (2013). Sizing truss structures using teaching-learning-based optimization. Comput. Struct. (119): 177-188. DOI: 10.1016/j.compstruc.2012.12.011.
  » https://doi.org/10.1016/j.compstruc.2012.12.011
• Dominguez, A., Stiharu, I., Sedaghati, R. (2006). Practical design optimization of truss structures using the genetic algorithms. Res. Eng. Des. (17): 73-84. DOI: 10.1007/s00163-006-0020-8.
  » https://doi.org/10.1007/s00163-006-0020-8
• Dorn,W.C., Gomory,R.E., Greenberg, H.J. (1964). Automatic design of optimal structures. J. Mecanique 3: 25-52.
• Fadel Miguel, L. F., Lopez, R. H., El Hami, A., Miguel, L. F. F. (2012). Firefly Metaheuristics for the Size, Shape and Topology Optimization of Truss Structures. In: Eleventh International Conference on Computational Structures Technology - CST 2012, Dubrovnik.
• Galante, M. 1996. Genetic Algorithms as an Approach to Optimize real world structures. Int J Numer. Meth. Eng. (39): 361-82. DOI: 10.1002/(SICI)1097-0207(19960215)39:3<361::AID-NME854>3.0.CO;2-1.
  » https://doi.org/10.1002/(SICI)1097-0207(19960215)39:3<361::AID-NME854>3.0.CO;2-1
• Goldberg, D.E., Samtani, M.P. (1986). Engineering optimization via genetic algorithms. Proceedings of the Ninth Conference on Electronic Computations, ASCE, Birmingham, Alabama, pp. 471-482,
• Goncalves, M. S., Lopez, R. H. , Miguel, L. F. F. (2015).Search group algorithm: a new metaheuristic method for the optimization of truss structures. Comput. Struct., 153:165-184. DOI: 10.1016/j.compstruc.2015.03.003.
  » https://doi.org/10.1016/j.compstruc.2015.03.003
• Grierson, D.E., Pak, W.H. (1993). Optimal sizing, geometrical and topological design using a genetic algorithms. Struct. Optimization (6): 151-9.
• Hajela,P., Lee, E. (1995). Genetic algorithms in truss topological optimization. Int. J. Solids Struct 32 (22): 3341-3357.
• Hajela,P., Lee, E., Lin,C.Y. (1993). Genetic algorithms in structural topology optimization Topology design of structures. M. P. Bendsoe and C. A. M. Soares, eds., Kluwer Academic, Dordrecht, The Netherlands, 117-133.
• Hansen, S.R., Vanderplaats, G.N. (1990). Approximation method for configuration optimization of trusses. AIAA J. 25, 161-168.
• Hasançebi, O. and Kazemzadeh Azad, S. (2014). Discrete size optimization of steel trusses using a refined big bang-big crunch algorithm. Eng. Optimiz. 46 (1): 61-83. DOI: 10.1080/0305215X.2012.748047.
  » https://doi.org/10.1080/0305215X.2012.748047
• Hasançebi, O., Kazemzadeh Azad, S. (2015). Adaptive Dimensional Search: A New Metaheuristic Algorithm for Discrete Truss Sizing Optimization. Computers and Structures. 154, 1-16.
• Jármai, K., Snyman, J.A., Farkas, J. (2004). Application of novel constrained optimization algorithms to the minimum volume design of planar CHS trusses with parallel chords. Eng. Optimiz. 36 (4): 457-471. DOI: 10.1080/03052150410001686495.
  » https://doi.org/10.1080/03052150410001686495
• Kaveh, A and Ahmadi, B. (2014). Sizing, geometry and topology optimization of trusses using force method and supervised charged system search. Structural Engineering and Mechanics. 50(3):362-282. DOI: 10.12989/sem.2014.50.3.365
  » https://doi.org/10.12989/sem.2014.50.3.365
• Kaveh, A. and Mahdavi., V.R. (2014). Colliding Bodies Optimization method for optimum design of truss structures with continuous variables. Adv, Eng. Softw. (70): 1-12. DOi: 10.1016/j.advengsoft.2014.01.002.
  » https://doi.org/10.1016/j.advengsoft.2014.01.002
• Kaveh, A. and Talatahari, S. (2009a). Size optimization of space trusses using Big Bang-Big Crunch algorithm. Comput. Struct. (87, 17-18): 1129-1140. DOI: 10.1016/j.compstruc.2009.04.011.
  » https://doi.org/10.1016/j.compstruc.2009.04.011
• Kaveh, A. and Talatahari, S. (2009b) . Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Comput. Struct. (87, 5-6), 267-283. DOI: 10.1016/j.compstruc.2009.01.003.
  » https://doi.org/10.1016/j.compstruc.2009.01.003
• Kaveh, A. and Zolghadr, A. (2014) A new PSRO algorithm for frequency constraint truss shape and size optimization. Structural Engineering and Mechanics. 52(3):445-468. DOI: 10.12989/sem.2014.52.3.445.
  » https://doi.org/10.12989/sem.2014.52.3.445
• Kaveh, A., Sheikholeslamib, R., Talataharic, S., Keshvari-Ilkhichib, M. (2014). Chaotic swarming of particles: A new method for size optimization of truss structures. Adv, Eng. Softw. (67): 136-147. DOI: 10.1016/j.advengsoft.2013.09.006.
  » https://doi.org/10.1016/j.advengsoft.2013.09.006
• Kazemzadeh Azad, S., Hasançebi, O. (2014). An Elitist Self-Adaptive Step-Size Search for Structural Design Optimization. Applied Soft Computing, 19, 226-235.
• Kazemzadeh Azad, S., Hasançebi, O. (2015a). Discrete sizing optimization of steel trusses under multiple displacement constraints and load cases using guided stochastic search technique. Structural and Multidisciplinary Optimization. 52, 383-404.
• Kazemzadeh Azad, S., Hasançebi, O., Saka, M.P. (2014). Guided stochastic search technique for discrete sizing optimization of steel trusses: A design-driven heuristic approach. Computers and Structures. 134, 62-74.
• Kelesoglu., O. (2007). Fuzzy Multiobjective Optimization of Truss-structures using genetic algorithms. Adv. Eng. Softw. (38):717-21. DOI: 10.1016/j.advengsoft.2007.03.003.
  » https://doi.org/10.1016/j.advengsoft.2007.03.003
• Koide, R. M., de França, G.V. Z., Luersen, M. A. (2013) an ant colony algorithm applied to lay-up optimization of laminated composite plates. Latin American Journal of Solids and Structures. 10(3).
• Kutyłowski R.a and Rasiak, B.b (2014). The use of topology optimization in the design of truss and frame bridge girders. Structural Engineering and Mechanics. 51(1): 67-88. DOI: 10.12989/sem.2014.51.1.067
  » https://doi.org/10.12989/sem.2014.51.1.067
• Lee, K.S., Geem,Z.W., Lee,S.-H.O. ,Bae,K.-W. (2005). The harmony search metaheuristic algorithm for discrete structural optimization. Eng. Optimiz. 37(7): 663-684.
• Li, J-P. (2014). Truss topology optimization using an improved species-conserving genetic algorithm. Eng. Optimiz. 47(1):107-128. DOI: 10.1080/0305215X.2013.875165.
  » https://doi.org/10.1080/0305215X.2013.875165
• Lobato, F.S., Steffen Jr, V. (2004) Fish swarm optimization algorithm applied to engineering system design. Latin American Journal of Solids and Structures. 11(1)
• Lopez, R. H., Luersen, M.A., Cursi, E.S. (2009a). Optimization of laminated composites considering different failure criteria. Compos. Part B-Eng 40:731-740. DOI: 10.1016/j.compositesb.2009.05.007.
  » https://doi.org/10.1016/j.compositesb.2009.05.007
• Lopez, R.H., Luersen, M.A., Cursi, E.S. (2009b). Optimization of Hybrid Laminated Composites using a Genetic Algorithm. J. Braz. Soc. Mech. Sci. 31(3): 269-278.
• Luh, G.C., Lin, C.Y. (2008). Optimal design of truss structures using ant algorithm. Structural and Multidisciplinary Optimization, 36(4), 365-379.
• Luh, G.C., Lin, C.Y. (2011). Optimal design of truss-structures using particle swarm optimization. Computers & Structures, 89(23), 2221-2232.
• Martini, K. (2011). Harmony Search Method for Multimodal Size, Shape, and Topology Optimization of Structural Frameworks. J. Struct. Eng. 137:11. DOI: 10.1061/(ASCE)ST.1943-541X.0000378.
  » https://doi.org/10.1061/(ASCE)ST.1943-541X.0000378
• Miguel, L. F. F.; Fadel Miguel, L. F.; Lopez, R. H. (2015). Simultaneous Optimization of Force and Placement of Friction Dampers Under Seismic Loading. Eng. Optimiz., accepted for publication.
• Miguel, L.F.F., Lopez, R.H., Miguel, L.F.F. (2013). Multimodal size, shape and topology optimization of truss structures using the firefly algorithm. Adv Eng. Softw. (56) 23-37. DOI: 10.1016/j.advengsoft.2012.11.006.
  » https://doi.org/10.1016/j.advengsoft.2012.11.006
• Miguel, L.F.F; Fadel Miguel, L. F. (2012) Shape and size optimization of truss structures considering dynamic constraints through modern metaheuristic algorithms. Expert Systems with Applications. 39, 9458-9467.
• Pereira, J. T., Fancello, E. A., & Barcellos, C. S. (2004). Topology optimization of continuum structures with material failure constraints. Structural and Multidisciplinary Optimization, 26(1-2), 50-66.
• Rajan, S. D. (1995). Sizing, shape, and topology design optimization of trusses using genetic algorithms. J. Struct. Eng. 121(10): 1480-1487.
• Rajeev, S., Krishnamoorthy,C.S. (1992). Discrete optimization of structures using genetic algorithms, J. Struct. Eng. 118 (5): 1233-1250.
• Rojas, J.E., Viana, F. A. C., Rade, D. A., Steffen Jr, V. (2004) Identification of external loads in mechanical systems through heuristic-based optimization methods and dynamic responses. Latin American Journal of Solids and Structures 1(3), 297-318.
• Sadollaha, A., Eskandarb, H., Bahreininejadc, A., Kim, J.H. (2015). Water cycle, mine blast and improved mine blast algorithms for discrete sizing optimization of truss structures. Comput. Struct. (149):1-16. DOI: 10.1016/j.compstruc.2014.12.003
  » https://doi.org/10.1016/j.compstruc.2014.12.003
• Salajegheh, E., Vanderplaats, G. (1993). Optimum design of trusses with discrete sizing and shape variables. Struct. Optimiz. 6:79-85.
• Sherestha, S.M., Ghaboussi, J, (1998). Evolution of optimum structural shapes using genetic algorithms. J. Struct. Eng. 123(11): 1331-8.
• Šilih,S.,Kravanja, S., Premrov, M. (2010). Shape and discrete sizing optimization of timber trusses by considering of joint flexibility. Adv. Eng. Softw. 41: 286-294. DOI:10.1016/j.advengsoft.2009.07.002.
  » https://doi.org/10.1016/j.advengsoft.2009.07.002
• Soh., C.K., Yang, J. (2005). Improved genetic algorithm for design optimization of truss structures with sizing, shape and topology variables. Int. J. Numer. Meth. Eng. (62):1737-1762.
• Sonmez, M. (2011). Discrete optimum design of truss structures using artificial bee colony algorithm. Struct. Multidiscip. O. 43:85-87. DOI 10.1007/s00158-010-0551-5.
  » https://doi.org/10.1007/s00158-010-0551-5
• Souza, R.R., Miguel, L.F.F., Lopez, R.H., Miguel, L.F.F, Torii, A.J. (2016) A procedure for the size, shape and topology optimization of transmission line tower structures. Engineering Structures, 111, 162-184.
• Tang, W., Tong,L., Gu,Y., (2005). Improved genetic algorithm for design optimization of truss structures with sizing, shape and topology variables. International Journal for Numerical Methods in Engineering 62:1737-1762.
• Tang. W., Tong. L., Gu, Y., (2005). Improved genetic algorithm for design optimization of truss structures with sizing, shape and topology variables. Int. J. Numer. Meth. Eng (62) 1737-1762.
• Torii, A. J.; Lopez, R. H.; Biondini, F. (2012). An approach to reliability-based shape and topology optimization of truss structures. Eng. Optimiz. (Print) 44: 37-53. DOI: 10.1080/0305215X.2011.558578.
  » https://doi.org/10.1080/0305215X.2011.558578
• Torii, A.J., Lopez, R. H., Luersen, M. (2011). A local-restart coupled strategy for simultaneous sizing and geometry truss optimization, Lat. Am. J. Solids Stru., 8, 335-349.
• Wu, C.Y., Tseng, K.Y. (2010). Truss structure optimization using adaptive multi-population differential evolution. Structural and Multidisciplinary Optimization, 42(4), 575-590.
• Wu, S.J., Chow,P.T., (1995). Integrated discrete and configuration optimization of trusses using genetic algorithms. Comput. Struct. 56(4):695-702.
• Zhanga, Y., Houa, Y. and Liua, S. (2014). A new method of discrete optimization for cross-section selection of truss structures. Eng. Optimiz. 46(8): 1052-1073. DOI: 10.1080/0305215X.2013.827671.
  » https://doi.org/10.1080/0305215X.2013.827671

APPENDIX A

On this section, the information regarding the best designs, for the studied examples, are presented on the following Tables.

Table A1:
Cross-sectional area values in cm² and weight in kg for the size, shape and topology optimization of the eleven-bar truss, on Section5.1.

Design variables	Rajan (1995)	Balling et. al. (2006)	Martini (2011)	Miguel et. al. (2013)	Present study
y1 (m)	19.987	-	-	-	20.057
y2 (m)	14.084	-	-	-	12.384
y3 (m)	4.7371	-	-	-	-
Member
2	74.193	-	-	74.193	74.193
3	23.226	-	-	18.581	18.581
4	74.193	-	-	37.032	37.032
5	63.871	-	-	74.193	74.193
6	9.677	-	-	46.581	46.581
8	67.097	-	-	-	-
9	77.419	-	-	87.097	87.097
10	60.645	-	-	-	-
OFE	3840	500000	4075	50000	50000
Weight (kg)	1475.999	1241.029	1315.418	1227.040	1227.070
Mean weight	-	-		1268.285	1265.654
C.O.V. (%)	-	-		2.12	2.02

Table A2:
Cross-sectional area values in cm² and weight in kg for the size and topology optimization of the thirty-nine-member truss, on Section 5.2.1.

Design variables	Deb and Gulati (2001)	Luh and Lin (2008)	Wu and Tseng (2010)	Lu and Lin (2011)	Miguel et al. (2013)	Present study
1	-	0.329	0.323	0.252	0.323	0.323
2	4.845	4.845	4.839	4.839	4.854	5.152
3	0.329	-	-	-	-	-
5	9.69	9.690	9.677	9.677	9.678	9.678
7	0.335	-	-	-	-	-
8	1.619	1.613	1.613	1.613	1.615	1.3
9	0.329	-	-	-	-	-
10	6.845	6.852	6.839	6.845	6.869	7.285
11	6.858	6.858	6.839	6.845	6.846	5.516
14	3.606	3.613	3.606	3.613	3.615	2.907
16	-	-	-	-	-	1.399
19	-	-	-	-	-	1.251
21	6.484	6.452	6.452	6.452	6.462	5.201
22	-	0.329	0.323	0.252	0.323	0.323
23	4.845	4.845	4.839	4.839	4.854	5.152
25	0.329	-	-	-	-	-
26	9.69	9.690	9.677	9.677	9.678	9.678
28	0.335	-	-	-	-	-
29	1.619	1.613	1.613	1.613	1.615	1.3
30	0.329	-	-	-	-	-
31	6.845	6.852	6.839	6.845	6.869	7.285
32	6.858	6.858	6.839	6.845	6.846	5.516
35	3.606	3.613	3.606	3.613	3.615	2.907
37	-	-	-	-	-	1.399
OFE	504000	303600	32300	262500	50000	50000
Weight (kg)	89.152	87.758	87.634	87.549	87.792	87.637
Mean weight	-	-	-	-	100.552	93.284
C.O.V. (%)	-	-	-	-	12.9	5.28

Table A3:
Cross-sectional area values in cm² and weight in kg for the size, shape and topology optimization of the thirty-nine-member truss, on Section 5.2.2.

Design variables	Deb and Gulati (2001)	Luh and Lin (2008)	Wu and Tseng (2010)	Lu and Lin (2011)	Miguel et al. (2013)	Ahrari, Atai and Deb (2014)	Present study
1	3.839	2.110	1.052	2.090	1.901	0.596102	2.879
2	7.523	7.065	9.735	7.058	6.87	6.321323	6.435
3	-	-	-	-	-	7.844571	2.575
4	-	-	-	-	7.686	7.110805	-
5	10.419	9.923	5.774	9.903	-	9.695815	10.112
6	-	-	-	-	-	3.610361	1.259
7	-	-	-	-	-	6.779051	0.336
8	0.329	0.523	1.097	-	8.1	-	-
10	7.452	7.877	7.245	7.877	-	5.310751	6.089
11	3.252	8.123	7.323	8.116	-	0.322935	5.483
12	-	-	-	0.529	-	-	3.437
14	8.342	3.387	3.503	3.387	0.326	2.334415	-
15	-	-	-	-	9.887	-	-
19	-	-	-	-	6.200	2.009196	-
20	-	-	-	-	-	-	2.29
21	8.761	8.103	7.135	8.097	-	-	5.351
22	3.839	2.110	1.052	2.090	1.901	0.596102	2.879
23	7.523	7.065	9.735	7.058	6.87	6.321323	6.435
24	-	-	-	-	-	7.844571	2.575
25	-	-	-	-	7.686	7.110805	-
26	10.419	9.923	5.774	9.903	-	9.695815	10.112
27	-	-	-	-	-	3.610361	1.259
28	-	-	-	-		6.779051	0.336
29	0.329	0.523	1.097	-	8.1	-	6.089
31	7.452	7.877	7.245	7.877	-	5.310751	-
32	3.252	8.123	7.323	8.116	-	0.322935	5.483
33	-	-	-	0.529	-	-	3.437
35	8.342	3.387	3.503	3.387	0.326	2.334415	-
36	-	-	-	-	9.887	-	-
OFE	504000	453600	137200	262500	50000	40256	50000
Weight (kg)	87.176	85.607	85.469	85.541	86.774	82.091	86.753
Mean weight (kg)	-	-	-	-	94.478	-	100.59
C.O.V.(%)	-	-	-	-	5.3	-	4.6

Table A4:
Cross sectional area (cm²) and weight (kg) for the size and shape optimization with buckling constraint of the 15-bar truss, on Section 5.3.1.

Design variables	Wu and Chow (1995)	Miguel et al. (2013)	Present study	Design variables	Wu and Chow (1995)	Miguel et al. (2013)	Present study
	GA	FA	BSA		GA	FA	BSA
A1	38.4	7.574	7.574	A13	8.6	8.6	8.6
A2	11.381	6.974	6.974	A14	11.381	1.852	2.839
A3	9.6	2.839	1.742	A15	11.381	8.6	6.155
A4	38.4	11.381	13.819	X2	301.98314	278.27986	334.33883
A5	13.819	9.6	8.6	X3	565.32526	571.15964	590.35225
A6	9.6	6.974	7.574	Y2	274.3708	262.41248	254
A7	18.064	0.716	0.716	Y3	315.13272	255.1049	254
A8	8.6	1.419	0.716	Y4	139.2809	131.00304	132.36646
A9	2.239	9.6	1.852	Y6	0.88138	43.3324	50.8
A10	6.974	1.123	0.91	Y7	39.41064	48.31588	50.8
A11	8.6	1.419	0.716	Y8	88.16594	124.06884	132.1094
	6.974	1.742	1.123
OFE	-	8000	8000
Minimum weight (kg)	182.506	62.627	59.641
Mean weight (kg)	-	69.948	64.049
C.O.V. (%)	-	3.85	3.96

Table A5:
Cross sectional area (cm²) and weight (kg) for the size, shape and topology optimization with buckling constraint of the 15-bar truss.

Design variables	Miguel et al. (2013)	BSA	Design variables	Miguel et al. (2013)	BSA
A1	6.155	6.155	A13	11.381	0
A2	6.155	6.155	A14	3.477	0
A3	0.716	6.155	A15	0	11.38
A4	13.819	13.819	X2	335.26984	322.4111
A5	6.974	8.6	X3	594.3219	561.5408
A6	8.6	0.91	Y2	293.11854	254
A7	0.716	1.742	Y3	296.89552	254
A8	1.419	3.478	Y4	134.7851	139.9969
A9	7.574	2.839	Y6	35.39998	-9.4016
A10	2.839	2.839	Y7	29.4767	50.8
A11	0	0	Y8	131.8133	138.7773
A12	0	1.742
OFE	8000	8000
Weight (kg)	56.803	54.827
Mean weight (kg)	69.223	60.187
C.O.V. (%)	8.69	7.88

Table A6:
Results for the size and shape optimization of the Twenty-five-bar 3D truss example.

Design variables	Rajeev and Krishnamoorthy (1992)	Wu and Chow (1995)	Tang et al. (2005)	Miguel et al. 2013	Gholaizedh (2013)	Present study
A1	0.6452	0.6452	0.6452	0.6452	0.6452	0.6452
A2	11.6129	1.2903	0.6452	0.6452	0.6452	0.6452
A3	14.8387	7.0968	7.0968	5.8064	6.4516	5.8064
A4	1.2903	1.2903	0.6452	0.6452	0.6452	0.6452
A5	0.6452	1.9355	0.6452	0.6452	0.6452	0.6452
A6	5.1613	0.6452	1.2903	0.6452	0.6452	0.6452
A7	11.6129	1.2903	1.2903	0.6452	0.6452	0.6452
A8	19.3548	5.8064	4.5161	6.4516	5.8064	6.4516
X4		104.3178	90.0938	94.7928	93.8530	90.8948
Y4		135.8138	153.3398	141.5796	138.6332	149.5881
Z4		316.4840	327.8378	321.6148	330.1238	310.1078
X8		129.0320	114.4524	127.3556	131.3942	127.4500
Y8		333.9592	348.0816	346.4560	354.4062	350.3897
OFE			6000	6000	8000	6000
Weight (kg)	247.6658	61.7792	56.6718	53.9003	53.1746	54.0189
Mean weight (kg)				60.010		61.8256
C.O.V. (%)				5.5		5.55

Table A7:
Results for the size, shape and topology optimization of the Twenty-five-bar 3D truss example.

Design variables	Rajeev and Krishnamoorthy (1992)	Wu and Chow (1995)	Tang et al. (2005)	Miguel et al. 2013	Gholaizedh (2013)	Present study
A1	0.6452	0.0000	0.0000	0.0000	0.0000	0.0000
A2	1.2903	0.6452	0.6452	0.6452	0.6452	0.6452
A3	7.0968	5.8064	7.0968	6.4516	5.8064	6.4516
A4	1.2903	0.0000	0.0000	0.0000	0.0000	0.0000
A5	1.9355	0.0000	0.0000	0.0000	0.0000	0.0000
A6	0.6452	0.6452	0.6452	0.6452	0.6452	0.6452
A7	1.2903	0.6452	0.6452	0.6452	0.6452	1.2903
A8	5.8064	7.0968	5.8064	5.8064	6.4516	5.8064
X4		100.3554	97.7900	98.7298	98.5266	92.2427
Y4		178.2572	163.4490	156.2608	167.9194	136.4609
Z4		267.1064	286.6898	302.7172	286.9692	324.5994
X8		140.0810	124.7902	125.5014	123.9266	112.7463
Y8		346.1258	342.7476	355.0768	352.7806	350.6709
OFE		6000	6000	8660	10000	6000
Weight (kg)	61.7792	53.8550	52.8798	51.8986	51.8728	53.9444
Mean weight (kg)			63.1219			66.8429
C.O.V. (%)			8			6.96

Publication Dates

• Publication in this collection
  Dec 2016

History

• Received
  18 May 2016
• Reviewed
  14 Sept 2016
• Accepted
  20 Sept 2016