Anisotropic elastic applications in composite materials using the isogeometric boundary element method

Abstract

This paper describes an isogeometric analysis of the boundary element method, called IGABEM, applied to anisotropic 2D plane elastic problems. The Lekhnitskii's anisotropic fundamental solution is used and the singular integral terms is regularized. For the weak singularity kernel, the Telles transform is used. On the other hand, in the strong singularity term, the Singularity Subtraction Technique - SST is used. The shape functions used are the Non-Uniform Rational B-Spline - NURBS. Thus, the same mathematical representation of Computer Aided Design - CAD is used in the implemented computational code. This avoids the generation of meshes and provides an exact representation of most complex geometries. As a reflection of this isoparametric concept, errors from geometric interpolation are excluded, improving numerical results. Furthermore, to increase the numerical efficiency of the code, the NURBS are decomposed into Bézier curves. To evaluate the accuracy of the formulation, complex problems using high-order isogeometric boundary elements are analyzed. Their results are compared to analytical solutions showing good agreement.

Keywords
Isogeometric analysis; NURBS; IGABEM; anisotropic elasticity; SST

Graphical Abstract

1 INTRODUCTION

As it is well known, Computer-Aided Design (CAD) programs use non-uniform rational B-Splines (NURBS) to model boundaries of solids. NURBS can exactly represent circles, ellipses, spheres, cylinders, and many other engineering geometries, which is not possible to obtain with the use of other functions such as, for example, polynomials, even those of higher order. Among the difficulties in working with high-order polynomials, we can highlight the globality: when changing any point of the curve, the entire curve will be affected. Therefore, when working with polynomials, it is usually necessary to divide a curve into elements. This behavior is not observed when using NURBS, because each control point only affects a portion of the whole curve (Cottrell et al., 2009). The NURBS geometric representation is typically smooth, whereas the representation for polynomials is typically continuous but not smooth. The ability to efficiently use a smooth basis in analysis has computational advantages over polynomials.

In this paper, NURBS are used not only to model geometry but also to approximate displacements and tractions throughout the boundary. NURBS curves are given through the Bézier extraction operator, which decomposes a set of NURBS basis functions for the Bernstein polynomial (Borden et al., 2011). This will allow the generation of continuous Bézier elements of class $C^0$, according to Beer and Duenser (2019), giving local representation of the basis functions, in addition to establishing a well-defined element from where collocation points are defined. The proposed Bézier elements provide a structure of elements for isogeometric analysis (Hughes et al., 2005), which is incorporated into the BEM, giving the idea of the isogeometric analysis boundary element method (IGABEM). Thus, the isoparametric concept is preserved, once that geometry, displacements, and tractions are interpolated by the same functions. Applications are presented for two-dimensional linear anisotropic elasticity problems, whose fundamental solution is written using through the formalism of Lekhnitskii (1968), in which the constitutive equation in terms of the flexibility tensor for the Airy stress is used. These fundamental solutions are present in several works and in different areas dealing with anisotropic elasticity, some of which are fracture mechanics (Rajapakse and Xu, 2001), (Albuquerque et al., 2004); bending problems (Pastorino et al., 2021); stress concentration factor (Özaslan et al., 2019). However, when using the fundamental solutions of Lekhnitskii, depending on the position of the collocation points of the discretized geometric region, singularities arise. These singular integrals are represented by the displacement (weak singularity) and traction (strong singularity) kernels. For weak singularity, the Telles transformation (Telles, 1987) was used, which develops a new transformation for the traditional Gaussian quadrature. And for strong singularity, the Singularity Subtraction Technique (SST) is used, as presented by Guiggiani (1998). The SST allows integration over high-order curved boundary elements, and this idea fits perfectly with the NURBS curves. In addition, according to Cordeiro and Leonel (2020), the SST is a methodology that can be applied to cores in a generic way since it does not impose any formal restrictions on the type of core to be integrated.

Therefore, this article presents an Isogeometric Analysis of the Boundary Element Method, with the anisotropic fundamental solution integrated by the Singularity Subtraction Technique - SST. As far as the authors know, the IGABEM for anisotropic materials has not yet been presented in the literature. Furthermore, the NURBS are decomposed into Bézier curves without the loss of continuity properties, which helps to reduce the cost of the developed computational algorithm. As a result, this formulation has superior accuracy when compared to codes that use the conventional MEC. Different numerical examples of simple and complex structures are presented to demonstrate the efficiency of the proposed methodology.

2 FUNDAMENTALS OF ANISOTROPIC ELASTICITY

If considered an infinitesimal element within the domain $\Omega$ the equilibrium of forces is expressed in the form${\sigma }_{ij,j}+\rho b_i=0$, where ${\sigma }_{ij}={\sigma }_{ji}$ is the stress tensor, $b_i$ is the vector of body forces, and$\rho$ is the density of the material. The traction at any point on the domain boundary $\Omega$is given by:

$$t_i={\sigma }_{ij}{n}_j,$$ (1)

where $n_j$ is the normal vector of the boundary. According to Hwu (2010), it is necessary to have the compatibility conditions for the deformation fields to guarantee the existence of a continuous displacement field of single value for a continuous body. Thus, the compatibility equation for infinitesimal deformation, given the symmetry of the deformations, for the two-dimensional case is satisfied if its derivatives obey the following relationship:

$$2{ϵ}_{\mathrm{12,12}}={ϵ}_{\mathrm{11,22}}+{ϵ}_{\mathrm{22,11}}.$$ (2)

Constitutive relationships for linear elastic material in an infinitesimal element, are related by generalized Hooke's law, as follows:

$${\sigma }_{ij}=C_{ijkl}{ϵ}_{kl},$$ (3)

$${ϵ}_{ij}=S_{ijkl}{\sigma }_{kl}.$$ (4)

The terms ${\sigma }_{ij}$ and ${ϵ}_{ij}$ are the second order stress and strain tensors, respectively. Each tensor is represented by nine index components $i,j=\mathrm{1,2,3}$. In Equation (3), the linearity coefficient is the fourth order tensor with 81 elements, called a tensor of elastic constants, which satisfies Green's symmetry conditions $C_{ijkl}$= $C_{klij}$= $C_{ijlk}$= $C_{jikl}$.

For plane stress or plane strain problems, Equation (4) can be written as:

$$\left\{\begin{array}{l}{\epsilon }_{11}\hfill \\ {\epsilon }_{22}\hfill \\ {\gamma }_{12}\hfill \end{array}\right\}=\left[\begin{array}{lll}{b}_{11}\hfill & b_{12}\hfill & b_{16}\hfill \\ b_{12}\hfill & b_{22}\hfill & b_{26}\hfill \\ b_{16}\hfill & b_{26}\hfill & b_{66}\hfill \end{array}\right]\left\{\begin{array}{l}{\sigma }_{11}\hfill \\ {\sigma }_{22}\hfill \\ {\sigma }_{12}\hfill \end{array}\right\}$$ (5)

where, $b_{ij}$ are given in terms of material compliance coefficients $a_{ij}$ (Lekhnitskii, 1968) as:

$$b_{ij}=a_{ij}\text{for plane stress}\text{,}$$ (6)

$$\begin{array}{l}{b}_{ij}=a_{ij}-\frac{a_{i3}{a}_{j3}}{a_{33}}\text{for plane strain}\text{,}\\ (i,j=\mathrm{1,2,6}).\end{array}$$ (7)

2.1 Formulation of the boundary integral equation

The boundary integral equation for anisotopic elastic problems can be derived from Betti's reciprocal theorem and Somigliana Identity, as can be seen in Gaul et al. (2013). Therefore, for a bidimensional anisotropic elastic problem of boundary $\Gamma$ and considering a null body forces, a boundary integral equation can be written in the form:

$$c_{ij}\left(x^{\prime }\right)u_i(x)+{\displaystyle {\int }_{\Gamma }{T}_{ij}}\left(x^{\prime },x\right)u_j(x)d\Gamma (x)={\displaystyle {\int }_{\Gamma }{U}_{ij}}\left(x^{\prime },x\right)t_j(x)d\Gamma (x)$$ (8)

The right hand side integral represents an integral in the sense of Cauchy main value, and $c_{ij}$ is the free coefficient term. In the case of this work, as the collocation points are always in a smooth part of the boundary, we have $c_{ij}={\delta }_{ij}/2$, were ${\delta }_{ij}$ is the Kronecker delta.

Fundamental solutions for plane anisotropic elasticity used in Equation (8) are based on the Airy stress function as seen in Lekhnitskii (1968). For 2D problems in plane strain state, the fundamental solution of displacement $U_{ij}$ and the fundamental solution of traction $T_{ij}$, which represent the displacement and the traction at the field point $z$, in the direction $j$, when the concentrated force is acting on the direction $i$ at the source point $z_0$, are given through a mapping in the complex plane, as:

$$\underset{\text{Source point}}{\underbracket{z_o=\left\{\begin{array}{c}{z}_{o1}\\ z_{o2}\end{array}\right\}=\left\{\begin{array}{l}{x}_{o1}+{\mu }_1{x}_{o2}\hfill \\ x_{o1}+{\mu }_2{x}_{o2}\hfill \end{array}\right\}}}\underset{\text{Field point}}{\underbracket{z=\left\{\begin{array}{l}{z}_1\hfill \\ z_2\hfill \end{array}\right\}=\left\{\begin{array}{l}{x}_1+{\mu }_1{x}_2\hfill \\ x_1+{\mu }_2{x}_2\hfill \end{array}\right\}}}.$$ (9)

Based on Equation (9), fundamental solutions of displacement and traction are written as follows:

$$U_{ij}\left(z,z_o\right)=2\mathrm{Re}\left[q_{i1}{A}_{j1}\ln \left(z_{o1}-z_1\right)+q_{i2}{A}_{j2}\ln \left(z_{o2}-z_2\right)\right],$$ (10)

$$T_{ij}\left(z,z_0\right)=2\mathrm{Re}\left[\frac{1}{\left(z_{o1}-z_1\right)}{g}_{j1}\left({\mu }_1{n}_1-n_2\right)A_{i1}+\frac{1}{\left(z_{o2}-z_2\right)}{g}_{j2}\left({\mu }_2{n}_1-n_1\right)A_{i2}\right],$$ (11)

where $\mathrm{Re}\left[\right]$ stands for the real part of the terms. Elements$\mathrm{}{q}_{ik}$, $g_{ji}$, and $A_{jk}$ can be seen in Sollero & Aliabadi (1993).

3 REPRESENTATION OF NURBS THROUGH BÉZIER EXTRACTION

Some geometric shapes are not possible to draw exactly using conventional polynomials. To solve this problem, rational functions, known as NURBS, are used as basis functions. With this basis is possible to achieve all forms of geometries, from the simplest to the most complex. In NURBS basis functions, in addition to the vector of nodes and the degree of the curve, it is necessary to introduce a weight vector. Thus, NURBS basis are defined through a weighted average between the B-Spline basis functions and may have a different weight for each control point.

From the algebraic point of view, a NURBS curve of grade $p$ is defined as:

$$\mathfrak{S}(t)={\displaystyle \sum _{i=1}^{n+1}{P}_i}{R}_{i,p}(t),$$ (12)

In Equation (12), the term $P_i$ are the control points, and the set $R_{i,p}(t)$ is the rational basis written as,

$$R_{i,p}\left(t\right)=\frac{w_i{\varphi }_{i,p}\left(t\right)}{{\displaystyle \sum _{j=1}^n{w}_j{\varphi }_{j,p}\left(t\right)}}=\frac{w_i{\varphi }_{i,p}\left(t\right)}{W\left(t\right)},$$ (13)

where ${\varphi }_{i,p}\left(t\right)$ is the basis B-Spline of degree $p$ for a vector of non-uniform knot written as $u=\left\{\mathrm{0,}\mathrm{0...,}\mathrm{0,}\mathrm{1,}\mathrm{...,1}\right\}$, $W\left(t\right)$, is the weight function. Equation (13) can also be written in the matrix form as:

$$R(t)=\frac{1}{W(t)}W\varphi (t)\text{where}W=\left[\begin{array}{llll}{W}_1\hfill & \hfill & \hfill & \hfill \\ \hfill & W_2\hfill & \hfill & \hfill \\ \hfill & \hfill & \ddots \hfill & \hfill \\ \hfill & \hfill & \hfill & W_3\hfill \end{array}\right].$$ (14)

Important characteristics for Equation (14) can be consulted in Hughes et al. (2005).

3.1 NURBS in the form of Bézier curves

The Bézier extraction operator for NURBS breaks down a set of NURBS base functions into Bernstein's polynomial. This allows the generation of continuous $C^0$ Bézier elements according to Beer et al. (2020), giving local representation of basis functions in addition to establishing a well-defined element where collocation points are located. The work of Borden et al. (2011) presented details of this methodology.

To build NURBS by Bézier curves, two steps are required: 1) Bézier decomposition, where all inner nodes are repeated by insertion of nodes up to multiplicity equal to $p$ and 2) Bézier extraction operator.

3.1.1 Insertion of knots

The refinement process is performed inserting new nodes $\overline{\xi }\in \left[{\xi }_k,{\xi }_{k+1}\right)$ to $k>p$ into the existing vector $U=\left\{{\xi }_0,{\xi }_1,{\xi }_2,\dots ,{\xi }_k,\overline{\xi },{\xi }_{k+1},\dots ,{\xi }_{m+p}\right\}$. New nodes are added at the midpoint between the old ones. In order to avoid change in the continuity of the curve, $m+2$ new control points are inserted. Furthermore, there is no change in geometric or parametric properties of the curve. Therefore, for each inserted node in the existing node vector, a new control point is added. This is done through:

$$\overline{P_i}\text{=}\left\{\begin{array}{l}{P}_1,\text{if}i=1\\ {\alpha }_i{P}_i+\left(1-{\alpha }_i\right)P_{i-1}\text{if}1<i<m\\ P_n\text{if}i=m\end{array}\right.\text{where}{\alpha }_i\text{=}\left\{\begin{array}{l}\text{1 if}1\le i\le k-p\\ \frac{\overline{\xi }-{\xi }_i}{{\xi }_{i+p}-{\xi }_i}\text{if}k-p+1\le i\le k\\ \text{0 if}i\ge k+1\end{array}\right..$$ (15)

According to Borden et al. (2011), the continuity of basis functions is reduced by one with each node insertion. However, by defining the new control point, the continuity of the curve is maintained.

3.1.2 Bézier decomposition

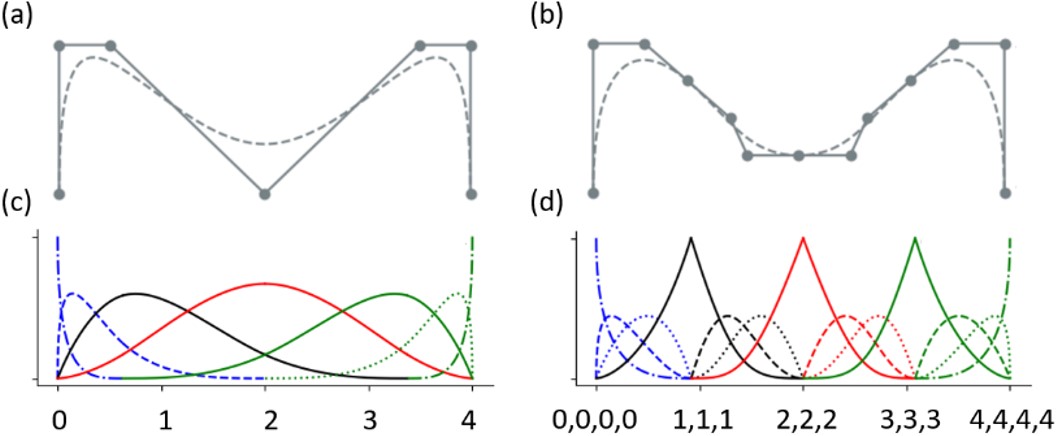
To illustrate the Bézier decomposition, consider Figure 1. In Figure 1(a) and 1(b) the NURBS curves are shown through the gray dashed line, constructed from the control points and their basis functions. The NURBS of Figure 1(a) was built using the basis functions obtained via conventional NURBS, as shown in Figure 1(c), while the NURBS of Figure 1(b) was constructed using the basis functions obtained via Bézier decomposition by the Bernstein polynomial, as shown in Figure 1(d). Figure 1 shows a cubic curve, whose associated node vector is $U=\left\{\mathrm{0,0,0,0,1,2,3,4,4,4,4}\right\}$. The process of decomposing the Bézier curve is carried out by inserting repeated nodes $\overline{U}=\left\{\mathrm{1,1,2,2,3,3}\right\}$ in all internal nodes, through Equation (15), until there is a multiplicity equal to the degree of the curve.

Figure 1
In (a) and (b) NURBS cubic curve and its control points. In (c) and (d) the basis functions of each curve.

According to Borden et al. (2011), it is important to highlight that those internal knots should have multiplicity $p+1$ to form Bézier elements. However, $p$ multiplicity is sufficient to represent Bernstein's polynomials, which in this context are also called Bézier basis functions. With each node that is inserted, the continuity of the basis functions is reduced by one degree at the knot location. Note that knots internal to element, $\xi =\mathrm{1,2}\text{and 3}$, Figure 1(c), appear only once in the knot vector and, therefore, the maximum possible continuity level $C^{p-1}=C^2$ is represented.

3.1.3 Bézier extraction operator

The Bézier extraction operator $C$ is constructed considering the $n$ control points and the $m$ knots necessary to perform the decomposition of the vector $U=\left({\overline{U}}_0,{\overline{U}}_1,\cdots ,{\overline{U}}_m\right)$ and ${\alpha }_j$ according to Equation (15). Equation (15) can be rewritten in matrix form to represent the sequence of control points created by inserting knots, as:

$${\overline{P}}^{j+1}={\left(C^j\right)}^t{\overline{P}}^j.$$ (16)

By repeating the form of Equation (16) $m$ times, the final set of control points ${\overline{P}}^{m+1}={\overline{P}}^b$ is defined for $C$ as:

$$C^t={\left(C^m\right)}^t{\left(C^{m-1}\right)}^t\cdots {\left(C^1\right)}^t.$$ (17)

In this way, Bézier elements are obtained through the final form of the decomposition, and the relationship between the new Bézier control points and the initial NURBS control points is written as:

$${\overline{P}}^b=C^{t}P.$$ (18)

Since, inserting a knot does not cause geometric or parametric changes in the curve, then, given the set of Bernstein basis functions defined by the knot vector $B_i(t)$ to $i=\mathrm{1,2,}\cdots ,n+m-1$, it is possible to obtain,

$${\left({\overline{P}}^b\right)}^{t}B(t)={\left(C^{t}P\right)}^{t}B(t)=P^{t}CB(t)=P^{t}N(t).$$ (19)

After matrix multiplication, Equation (19) is written as,

$$CB(t)=\varphi (t),$$ (20)

where $C$ is called the Bézier extraction operator and depends only on the knot vector. Note that $B$ is represented as class $C^0$, and $C$ maps the Bernstein polynomial basis piecewise into NURBS, performing the linear combination of the Bézier basis functions. Thus, when writing $CB$, this term reverts to the continuity of the original NURBS.

Inserting Equation (20) into Equation (14), the NURBS basis functions using the Bézier extraction operator, becomes:

$$R(t)=\frac{1}{W(t)}WCB(t).$$ (21)

In this format, Equation (21) is ready to be used as a shape function in the discretization of IGABEM.

4 ISOGEOMETRIC BOUNDARY ELEMENTS

In IGABEM, the definition of curves is based on patch which are the knots in the $\left[{\xi }_1,{\xi }_{n+p+1}\right]$ interval and the $\left[{\xi }_i,{\xi }_{i+1}\right]$ interval are the knots span, $\xi$ being the Gaussian element, $\xi \in [-\mathrm{1,1}]$. In IGABEM, it is necessary to construct a term of connectivity between elements, in which a set of local basis functions are related to global functions in the form ${\varphi }_c^e\equiv R_{n,p}(\xi )$. The number of the local basis function $(c)$, the element number $(e)$ and the number of the global basis function are related by a connectivity function, see (Simpson et al. 2013). From this connectivity between elements, it is possible to establish isogeometric approximations for the geometric element, and the geometry of the problem is described using the basis functions as follows:

$$x_e(\xi )={\displaystyle \sum _{c=1}^{p+1}{\varphi }_c^e}(\xi )x_c^e.$$ (22)

Displacements and tractions are written as:

$$u_e(\xi )={\displaystyle \sum _{c=1}^{p+1}{\varphi }_c^e}(\xi )u_c^e,$$ (23)

$$t_e(\xi )={\displaystyle \sum _{c=1}^{p+1}{\varphi }_c^e}(\xi )t_c^e,$$ (24)

where $x_c^e$, $u_c^e$ and $t_c^e$ are vectors of the geometric coordinates, displacement coefficients and traction coefficients respectively, associated with the control point corresponding to the basis function $c$ for the Bézier curve $e$. It is important to note that the term coefficient is used, since NURBS basis functions do not necessarily obey the Kronecker delta property. Therefore $u_c^e$ and $t_c^e$ represent the displacements and traction at collocation points that may not belong to the domain (Simpson et al. 2013).

Using Equations (23) and (24), in Equation (8), we have:

$$c_{ij}\left(x^{\prime }\right){\displaystyle \sum _{l=1}^{p+1}{\varphi }_l^{\overline{e}}}\left({\xi }^{\prime }\right)u_j^{le}+{\displaystyle \sum _{e=1}^{N_e}{\displaystyle \sum _{l=1}^{p+1}\left[{\displaystyle {\int }_{-1}^1{T}_{ij}}\left(x^{\prime },x(\xi )\right){\varphi }_l^e(\xi )J(\xi )d\xi \right]}}{u}_j^{le}\text{=}{\displaystyle \sum _{e=1}^{N_e}{\displaystyle \sum _{l=1}^{p+1}\left[{\displaystyle {\int }_{-1}^1{U}_{ij}}\left(x^{\prime },x(\xi )\right){\varphi }_l^e(\xi )J(\xi )d\xi \right]}}{t}_j^{le},$$ (25)

where $u_j^{le}$ and $t_j^{le}$ represent the components of vectors $u_c^e$ and $t_c^e$, and $J$ is the Jacobian of the transformation. In conventional BEM, the Kronecker delta property of the basis functions guarantees that the basis functions are interpolating. In the IGABEM, on the other hand, it cannot guarantee that this is true, and the displacement must be given as $u_i(x)={\displaystyle \sum _{l=1}^{p+1}{\varphi }_l^{\overline{e}}}\left({\xi }^{\prime }\right)d_j^{l\overline{e}}$, where ${\xi }^{\prime }$ is the local coordinate of the collocation point in the element $\overline{e}$.

The Bézier extraction operator promotes the construction of elements very similar to the one used in the conventional BEM. Each patch of the parametric space corresponds to an element independent of the adjacent elements, which, in turn, corresponds to the parametric subintervals adjacent to the initial one. Thus, in this paper, Equation (25) is applied to each control point. Finally, a non-sparse and non-symmetric matrix algebraic system is obtained as follows:

$$Hu=Gt,$$ (26)

where $H$ and $G$ are influence matrices. Note that the control points, except for rectilinear geometries, do not belong to the NURBS curve. And so, the boundary conditions cannot be applied directly to Equation (26). To solve this problem, an $E$ transformation matrix for NURBS is generated according to Cabral et al., (1990). This matrix uses basis functions to relate the values at the control points to the values at the collocation points, in the form:

$$u=E{u}_c,$$ (27)

$$t=E{t}_c,$$ (28)

where $u$ and $t$ are the vectors containing the displacements and tractions at the collocation points, $u_c$ and $t_c$ are vectors containing values at the control points. Now, Equations (27) and (28) can be applied to Equation (26):

$$H{E}^{-1}u=G{E}^{-1}t.$$ (29)

Reorganizing the known and unknown terms of Equation (29) we arrive at a linear equation system of the type $Ax=b$. Where $x$ is the solution vector of unknown tractions and displacements.

4.1 Strategy for the generation of collocation points

As commented, control points may not be necessarily on the curve, but on the control polygon. This is not the best choice for collocation points in the BEM. In Li & Qian (2011), different forms of distribution for the collocation points were tested. Based on their results, the Greville coordinates is the best choice, with stable and accurate results for the isogeometric method. Thus, the Greville abscissa used here is defined as the mean value of knots:

$${\xi }_i^{\text{'}}=\frac{{\xi }_{i+1}+{\xi }_{i+2}+\dots +{\xi }_{i+p}}{p}.$$ (30)

When the curve is smooth, Greville coordinates are perfect to be use as collocation points. Otherwise, when there are corners, in order to avoid collocation points at corners, it is proposed to change the positions of the first and last collocation point:

$${\xi }_1^{\text{'}}={\xi }_1^{\text{'}}+s\left({\xi }_2^{\text{'}}-{\xi }_1^{\text{'}}\right),$$ (31)

$${\xi }_n^{\text{'}}={\xi }_n^{\text{'}}-s\left({\xi }_n^{\text{'}}-{\xi }_{n-1}^{\text{'}}\right),$$ (32)

where $s$ is a coefficient that defines how much the collocation point moves. As shown by Wang & Benson (2015), an optimal value is $s=0.5$.

4.2 Singular integrals

In the conventional BEM, only one basis function associated with an element is non-zero at a given collocation point. This is not true for IGABEM, since more than one basis functions can be different from zero at the collocation point. Therefore, there is only one singular integral in each element. While in NURBS, the basis functions do not have this characteristic, as several of them can be non-null in the collocation points. For each collocation point there are $k$ singular integrals. This characteristic related to the analysis of singularities in IGABEM is a crucial point to solve the BIE.

The fundamental displacement solution containing the weak singularity was treated in this work with the Telles transform. Details about this method will not be given here, once it can be found in Telles (1987). On the other hand, for traction equation, the Subtraction Singularity Technique (SST) seen in Guiggiani (1998) is used. It is based on the expansion of the kernel in series for the treatment of singularities. In general, this technique is formulated based on the substitution of the singular integral, creating two new terms: a new regular kernel and a new singular integral, in such a way that the latter can be integrated analytically.

The first step of this method is to consider the expansion of $z_k$, which is the complex mapping shown in Equation (9), in Taylor series around the singular term ${\xi }_0$, which becomes:

$$z_i^{*}(\xi )=z_i\left({\xi }_0\right)+{\left.\left(\xi -{\xi }_0\right)\frac{\partial z_i}{\partial \xi }\right|}_{\xi ={\xi }_0}+O{\left(\xi -{\xi }_0\right)}^2.$$ (33)

Expanding the derivative in Equation (27), it becomes:

$${\left.\frac{\partial z_i}{\partial \xi }\right|}_{\xi ={\xi }_0}={\left.\frac{\partial z_i}{\partial x_1}\frac{\partial x_1}{\partial \xi }\right|}_{\xi ={\xi }_0}+{\left.\frac{\partial z_i}{\partial x_2}\frac{\partial x_2}{\partial \xi }\right|}_{\xi ={\xi }_0}.$$ (34)

Now, substituting Equation (34) into Equation (33), results in:

$$z_i^{*}(\xi )=z_i\left({\xi }_0\right)+\left(\xi -{\xi }_0\right)\left(\frac{\partial z_i}{\partial x_1}\frac{\partial x_1}{\partial \xi }+\frac{\partial z_i}{\partial x_2}\frac{\partial x_2}{\partial \xi }\right)+O{\left(\xi -{\xi }_0\right)}^2.$$ (35)

It is worth remembering that the unit vector $n$ which is normal to the boundary $\Gamma$, and its components in $x_1$ and in $x_2$ directions are written as $n_{x1}$ and $n_{x2}$ in the form:

$$n\left({\xi }_0\right)=\left(\frac{\partial x_2}{\partial \xi }i-\frac{\partial x_1}{\partial \xi }j\right)/J\left({\xi }_0\right)\to n_{x1}\left({\xi }_0\right)=\frac{\partial x_2}{\partial \xi }/J\left({\xi }_0\right)\text{e}{n}_{x2}\left({\xi }_0\right)=\frac{\partial x_1}{\partial \xi }/J\left({\xi }_0\right).$$ (36)

From Equation (36) one arrives at:

$$\frac{\partial x_1}{\partial \xi }=-J\left({\xi }_0\right)n_{x2}\left({\xi }_0\right)\text{and}\frac{\partial x_2}{\partial \xi }=J\left({\xi }_0\right)n_{x1}\left({\xi }_0\right)$$ (37)

So when replacing Equation (37) in Equation (35), it is possible to find the following equation:

$$z_i^{*}(\xi )=z_i\left({\xi }_0\right)+\left(\xi -{\xi }_0\right)J\left({\xi }_0\right)\left(\frac{\partial z_i}{\partial x_2}{n}_{x1}\left({\xi }_0\right)-\frac{\partial z_i}{\partial x_1}{n}_{x2}\left({\xi }_0\right)\right)+O{\left(\xi -{\xi }_0\right)}^2$$ (38)

where

$$\left\{\begin{array}{l}\frac{\partial z_i}{\partial x_1}=\frac{\partial }{\partial x_1}\left[x_1+{\mu }_i{x}_2\right]=\mathrm{1,}\\ \frac{\partial z_i}{\partial x_2}={\mu }_i.\end{array}\right.$$ (39)

Through Equation (38), we arrive at the final expression for the expansion of $z_k$ around ${\xi }_0$, writing as:

$$z_i^{*}(\xi )=z_i\left({\xi }_0\right)+\left(\xi -{\xi }_0\right)J\left({\xi }_0\right)\left({\mu }_i{n}_{x1}\left({\xi }_0\right)-n_{x2}\left({\xi }_0\right)\right)+O{\left(\xi -{\xi }_0\right)}^2.$$ (40)

The expansion written in this form as presented by Cordeiro & Leonel (2020), when replaced in the strongly singular integral, can isolate singularities of kernels of integrals. Therefore, for the regularization process of the strongly singular term, expanded auxiliary kernels for the boundary will be added and subtracted. Then, the strongly singular term is written as:

$${\displaystyle {\int }_{-1}^1{T}_{ij}}\left({\xi }_0,\xi \right){\varphi }_k(\xi )J(\xi )d\xi ={\displaystyle {\int }_{-1}^1\left[K_T\left({\xi }_0,\xi \right)-K_T^{*}\left({\xi }_0,\xi \right)\right]}d\xi +{\displaystyle {\int }_{-1}^1{K}_T^{*}}\left({\xi }_0,\xi \right)d\xi .$$ (41)

Note that, in the integral on the left hand side of Equation (41), ${\varphi }_k(\xi )$ is the basis function that approximates the $u_j\left(x\right)$ term and $J(\xi )$ is the parameter that transforms the dimensionless coordinate to real coordinates. While the terms of the right-hand integrals $K_T({\xi }_0,\xi )$ are the original kernels of the integral, that is:

$$K_T\left({\xi }_0,\xi \right)=T_{ij}\left({\xi }_0,\xi \right){\varphi }_k(\xi )J(\xi ),$$ (42)

and $K_T^{*}({\xi }_0,\xi )$ is written in the form of the expansion of the Taylor series around $\xi ={\xi }_0$, obtained through the linear term of the expansion of Equation (40).

$$K_T^{*}\left({\xi }_0,\xi \right)=2\mathrm{Re}\left[\frac{T_{ijl}\left({\xi }_0\right)}{z_l^{*}(\xi )-z_l\left({\xi }_0\right)}\right]{\varphi }_k^{*}(\xi )J^{*}(\xi ),$$ where $$T_{ijl}({\xi }_0)=g_{jl}({\mu }_l{n}_{x1}({\xi }_0)-n_{x2}({\xi }_0))A_{il}$$.(43)

When analyzing Equation (41) after replacing Equations (42) and (43), the strong singularity $1/(z_l^{*}(\xi )-z_l({\xi }_0))$ is noted. To regularize the integral between square brackets of Equation (43), Marczak & Creus (2002) used the first-order term of the expansion of the basis function. On the other hand, Cordeiro & Leonel (2020) considered only the constant term of the ${\varphi }_k^{*}(\xi )={\varphi }_k({\xi }_0)$ expansion. As it has been shown that only one term is necessary for an adequate representation, then only the constant expansion term is used in this work, and with that, the integral between square brackets of Equation (41) is solved numerically by the Gauss Legendre quadrature. On the other hand, the other integral on the right side is still singular and must be solved analytically in the sense of the Cauchy Principal Value - CPV through a limit analysis. So $K_T^{*}({\xi }_0,\xi )$ is written as:

$$\begin{array}{l}{\displaystyle {\int }_{-1}^1{K}_T^{*}}\left({\xi }_0,\xi \right)d\xi =\underset{\xi \to {\xi }_0}{\lim }{\displaystyle {\int }_{-1}^{1}2}\mathrm{Re}\left[\frac{T_{ijl}\left({\xi }_0\right)}{z_l^{*}(\xi )-z_l\left({\xi }_0\right)}\right]{\varphi }_k(\xi )J(\xi )d\xi \\ ={\varphi }_k\left({\xi }_0\right)J\left({\xi }_0\right)2\mathrm{Re}\left\{g_{jn}\left({\mu }_l{n}_{x1}\left({\xi }_0\right)-n_{x2}\left({\xi }_0\right)\right)A_{in}\underset{\xi \to {\xi }_0}{\lim }\left[{\displaystyle {\int }_{-1}^1\frac{1}{z_l^{*}(\xi )-z_l\left({\xi }_0\right)}}d\xi \right]\right\}.\end{array}$$ (44)

From Equation (40), it is possible to find the relationship:

$$\frac{1}{\left(\xi -{\xi }_0\right)J\left({\xi }_0\right)}=\frac{{\mu }_i{n}_{x1}\left({\xi }_0\right)-n_{x2}\left({\xi }_0\right)}{z_i^{*}(\xi )-z_i\left({\xi }_0\right)}.$$ (45)

Thus, it is possible to remove the term that is replaced in Equation (44), which is now written as:

$$\begin{array}{l}{\displaystyle {\int }_{-1}^1{K}_T^{*}}\left({\xi }_0,\xi \right)d\xi ={\varphi }_k\left({\xi }_0\right)J\left({\xi }_0\right)2\mathrm{Re}\left\{g_{jn}{A}_{in}\underset{\xi \to {\xi }_0}{\lim }\left[{\displaystyle {\int }_{-1}^1\frac{{\mu }_i{n}_{x1}\left({\xi }_0\right)-n_{x2}\left({\xi }_0\right)}{z_i^{*}(\xi )-z_i\left({\xi }_0\right)}}d\xi \right]\right\}\\ ={\varphi }_k\left({\xi }_0\right)J\left({\xi }_0\right)2\mathrm{Re}\left\{g_{jn}{A}_{in}\underset{\xi \to {\xi }_0}{\lim }\left[{\displaystyle {\int }_{-1}^1\frac{1}{\left(\xi -{\xi }_0\right)J\left({\xi }_0\right)}}d\xi \right]\right\}\\ ={\varphi }_k\left({\xi }_0\right)2\mathrm{Re}\left\{g_{jn}{A}_{in}\text{CPV}\frac{1}{\left(\xi -{\xi }_0\right)}\right\}.\end{array}$$ (46)

Therefore, with Equation (46) it is possible to calculate the singular integral in a regular way using the limit $\text{CPV}\left[1/(\xi -{\xi }_0)\right]=\text{ln}(1-{\xi }_0)-\text{ln}(1+{\xi }_0)$.

It is necessary to draw attention to an important fact in the work of Cordeiro & Leonel (2020). Their final equation to regularize the strongly singular term, similar to Equation (46), has a Jacobian $J({\xi }_0)$ on the right side of the equation. However, when using Equation (45) in Equation (46), this Jacobian is canceled out and at this point this equation differs from theirs.

4.3 Treatment of body forces

In order to efficiently apply the boundary element method without volume integration for problems involving body forces, such as gravity and centrifugal force, the present authors used the modified boundary conditions method in the context of anisotropic plane elasticity. This method was used by Caicedo & Portela (2017) and by Oliveira and Portela (2019) to regularize singular stress fields at the tip of cracks in applications of the finite element method and meshless methods, respectively. In the case of this work, the method is the same, but the objective is different from that presented in the literature. The particular solutions used for domain integrals are those presented by Deb and Banerjee (1990). In the work of Deb and Banerjee (1990), an extra integral was generated in the boundary integral equation, which led to a new vector in the matrix equation. However, in this work, no extra integrals are generated, only the boundary conditions are modified.

By decomposing the elastic field a homogeneous part $H$ and a particular part $P$, stresses and displacement can be written as:

$${\sigma }_{ij}=\left({\sigma }_{ij}-{\sigma }_{ij}^P\right)+{\sigma }_{ij}^P={\sigma }_{ij}^H+{\sigma }_{ij}^P,$$ (47)

$$u_i=\left(u_i-u_i^P\right)+u_i^P=u_i^H+u_i^P,$$ (48)

where ${\sigma }_{ij}^H={\sigma }_{ij}-{\sigma }_{ij}^P$ and $u_i^H=u_i-u_i^P$ are respectively the homogeneous solutions for the stress and displacement fields that is, disregarding the body forces of the original problem, ${\sigma }_{ij}^P$ and $u_i^P$ are respectively the stress and displacement particular solutions of the original problem, representing the elastic field with the body forces.

Considering that the body forces is due to the rotation of the body (centrifugal load), the motion equation is given by:

$${\sigma }_{ij,j}+\rho {\omega }^2{x}_i=0$$ (49)

Particular solutions for this equation can be found in Deb and Banerjee (1990). For displacements, we have:

$$u_1^p=\frac{1}{3}\left\{\left(b_{11}+b_{12}\right)c_1+b_{11}{c}_2\right\}{x}_1^3+\frac{1}{2}{b}_{16}{c}_2{x}_1^2{x}_2+\left\{\left(b_{11}+b_{12}\right)c_1+b_{12}{c}_2\right\}{x}_1{x}_2^2+\frac{1}{3}\left\{\left(b_{16}+b_{26}\right)c_1+\frac{1}{2}{b}_{26}{c}_2\right\}{x}_2^3,$$ (50)

$$u_2^p=\frac{1}{3}\left\{\left(b_{16}+b_{26}\right)c_1+\frac{1}{2}{b}_{26}{c}_2\right\}{x}_1^3+\left\{\left(b_{22}+b_{12}\right)c_1+b_{12}{c}_2\right\}{x}_1^2{x}_2+\frac{1}{2}{b}_{26}{c}_2{x}_1{x}_2^2+\frac{1}{3}\left\{\left(b_{22}+b_{12}\right)c_1+b_{22}{c}_2\right\}{x}_2^3.$$ (51)

And for stress, we have:

$${\sigma }_{11}^p=c_1\left(x_1^2+x_2^2\right)+c_2{x}_1^2,$$ (52)

$${\sigma }_{22}^p=c_1\left(x_1^2+x_2^2\right)+c_2{x}_2^2,$$ (53)

$${\sigma }_{12}^p=c_2{x}_1{x}_2.$$ (54)

Components$c_1$ and $c_2$ are represented in the form of Equations (55) and (56), for the plane stress state and for plane strain state, according the Equations (6) and (7), respectively.

$$c_1=\frac{4b_{12}-b_{66}}{2\left(3b_{11}+2b_{12}+3b_{22}+b_{66}\right)}\rho {\omega }^2,$$ (55)

$$c_2=-\frac{b_{11}+2b_{12}+b_{22}}{3b_{11}+2b_{12}+3b_{22}+b_{66}}\rho {\omega }^2.$$ (56)

where $\rho$ is the density of the material and $\omega$ is the angular velocity.

5 NUMERICAL RESULTS

In order to assess the proposed method, four applications were analyzed, with different mesh refinements and curve orders. The first application is a problem of elastic analysis in an orthotropic rotating disk, whose analytical solution was presented by Chang (1974). The second application is the determination of the stress concentration factor in an infinity plate, whose analytical solution was presented by Lekhnitskii (1968). The third application is the calculation of the stress distribution in a rectangular plate. In this one, the solution was the same used in Nuismer & Whitney (1975). Finally, the fourth application is the calculation of the tangential stress distributions along the circumference of a hole, whose analytical solution was presented by Lekhnitskii (1968).

5.1 Elastic analysis on a rotating disk under constant angular velocity.

Consider an orthotropic rotating disk, of radius $R$, as shown in Figure 2. The disk is in a plane stress state, at a constant angular velocity $\omega$. The direction of the longitudinal and transversal elastic module $E_1$ and $E_2$ respectively, are also shown in Figure 2. Equations representing stress tensor components were given by Chang (1974). When evaluated in polar coordinates, stress tensor components are written as:

Figure 2
Representation of the orthotropic rotating disk.

$$\begin{array}{l}{\sigma }_r=\frac{1}{2}\rho {\omega }^2(1-K)\left(R^2-r^2\right),\\ {\sigma }_t=\frac{1}{2}\rho {\omega }^2\left(K\left(3r^2-R^2\right)+\left(R^2-r^2\right)\right)n,\\ {\sigma }_{rt}=\mathrm{0,}\end{array}$$ (57)

where ${\sigma }_r$ is the radial stress, ${\sigma }_t$ is the tangential stress (circumferential), and ${\sigma }_{rt}$ is the shear stress. Finally, the equations for displacement vector components are written as:

$$u_1=\frac{a_{11}\rho {\omega }^{2}x}{2}\left\{K\left(\frac{x^2}{3}+3y^2-R^2\right)+\left(R^2-\left(\frac{x^2}{3}+y^2\right)\right)\right\}+\frac{a_{12}\rho {\omega }^{2}x}{2}\left\{K\left(x^2+y^2-R^2\right)+\left(R^2-\left(\frac{x^2}{3}+y^2\right)\right)\right\},$$ (58)

$$u_2=\frac{a_{12}\rho {\omega }^{2}y}{2}\left\{K\left(x^2+y^2-R^2\right)+\left(R^2-\left(x^2+\frac{y^2}{3}\right)\right)\right\}+\frac{a_{22}\rho {\omega }^{2}y}{2}\left\{K\left(3x^2+\frac{y^2}{3}-R^2\right)+\left(R^2-\left(x^2+\frac{y^2}{3}\right)\right)\right\}.$$ (59)

where the radial displacement is written through Equations (58) and (59) in the form $u_r=u_1^2+u_2^2$.

Considering symmetry, the problem can then be simulated by modeling a quarter of the disk, as shown in Figure 3. The model geometry was built with three NURBS curves $\left(N_1\right.$, $N_2$, and $\left.N_3\right)$ as shown in Figure 3. Boundary conditions (bc) are given by Equation (60).

Figure 3
A quarter of the orthotropic rotating disk.

$$\text{bc:}\left\{\begin{array}{l}{t}_x=u_y=\mathrm{0,}(x,y)\in N_1,\\ \\ t_x=t_y=\mathrm{0,}(x,y)\in N_2,\\ \\ u_x=t_y=\mathrm{0,}(x,y)\in N_3.\end{array}\right.$$ (60)

Table 1 presents elastic constants and the geometric information used in the simulation of the problem.

Table 1
Mechanical properties of the material and geometric information: problem 01.

Description of variables	Values of variables	Description of variables	Values of variables
Longitudinal elastic modulus	$E_1=17.24\text{GPa}$	Laminate Layers	$C=2$
Transverse elastic modulus	$E_2=48.26\text{GPa}$	Fiber direction	$\theta =0^{\circ }$
Poisson's coefficient	${\nu }_{12}=0.29$	NURBS degree	$p=2$
Shear module	$G_{12}=6.89\text{GPa}$	Radius	$R=1\text{m}$
Angular velocity	$\omega =20\text{rad/s}$	Density	$\rho =1{\text{kg/m}}^3$

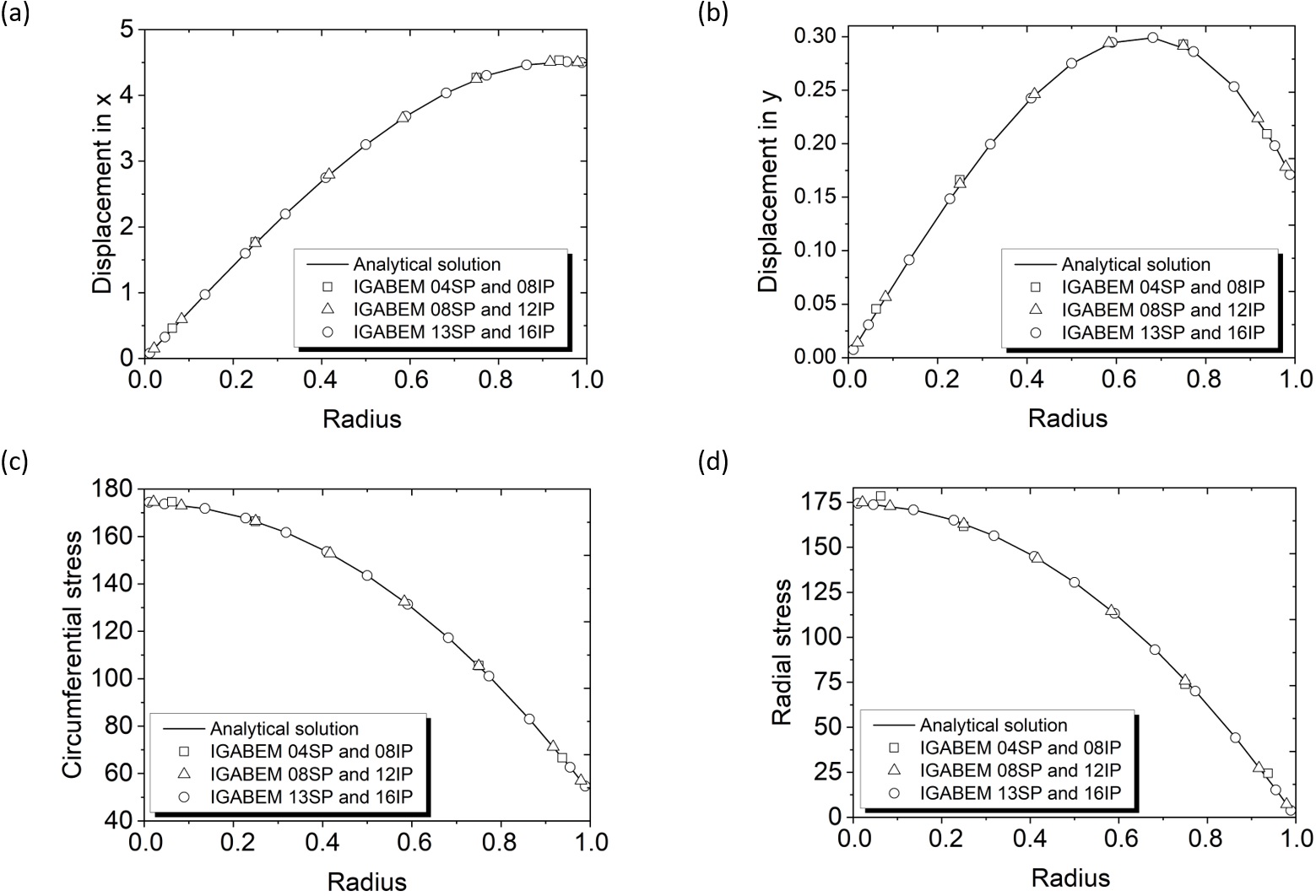
The quarter of the disk was modeled with different amount of Source Points - SP and Integration Points - IP, as can be seen in Figure 4. These quantities are defined by each NURBS, such as 04SP and 08IP. This means the total geometry has 12 source points. Numerical results for displacements are presented for the $N_1$ edge in Figure 4(a) and for the $N_3$ edge in Figure 4(b). The circumferential stress is shown in Figure 4(c) and the radial stress in Figure 4(d), for the $N_1$ edge. Numerical results show that the mesh refinement with 4 source points already presents good agreement with analytical solutions. On the other hand, the number of integration points has strong influence on the numerical results, as shown in Figure 4.

Figure 4
(a) Displacement on edge $N_1$, (b) displacement on edge $N_3$, (c) radial stress and (d) circumferential stress .

In order to identify the influence of mesh refinement on the numerical error, the study of convergence for displacements and stresses was carried out using a relative error measurement:

$$\epsilon =\frac{\sqrt{{{\displaystyle \sum _{i=1}^n\left|\underset{analytical}{\underbrace{u_i}}-\underset{numerical}{\underbrace{\overline{u_i}}}\right|}}^2}}{\sqrt{n}},$$ (61)

where $\epsilon$ is the Euclidean norm of the difference between analytical and numerical solutions and $n$ is the total number of NURBS source points. Results for the errors are shown in Figure 5, with displacements at edge $N_1$ and at edge $N_3$being shown in Figure 5(a), and circumferential stress and radial stress error in Figure 5(b), for the edge $N_1$. These errors represent global errors computed 0,at edges $N_1$, $N_2$, and $N_3$.

Figure 5
Error$\epsilon$: (a) displacement in $x$ and $y$, (b) Circumferential and radial stress.

5.2 Stress concentration factor in a circular hole in a plate of infinite dimensions.

Consider a plate of infinite dimensions with a circular hole as shown in Figure 6. The aim of this example is the computation of the Stress Concentration Factor - SCF on a rectangular plate of an anisotropic material, with constant thickness and under an infinite with load $\overline{\sigma }$ in the $y$ direction. This problem is a good example to illustrate the efficiency of higher-order IGABEM, mainly for modeling the curved hole boundary around which stresses vary rapidly. According to Lekhnitskii (1968) the stress concentration factor for an orthotropic material on a plate of infinite width is given by:

Figure 6
Plate with hole in infinite plane with uniform stress in $y$axis.

$$K_{\text{T},\text{MAX}}^{\infty }=1+\sqrt{\frac{2}{A_{22}}\left(\sqrt{A_{11}{A}_{22}}-A_{12}+\frac{A_{11}{A}_{22}-A_{12}^2}{2A_{66}}\right)},$$ (62)

where $A_{ij}$ are laminate stiffness matrix terms. For the anisotropic SCF, Konish & Whitney (1975) was used, as:

$$K_{\text{T},\text{MAX}}^{\infty }=\frac{{\sigma }_y(r\mathrm{,0})}{\overline{\sigma }}=\overline{\sigma }\mathrm{Re}\left[1+i\left(\frac{1}{{\mu }_1}+\frac{1}{{\mu }_2}\right)\right],$$ (63)

where ${\mu }_i$ are roots of the characteristic equation for an anisotropic material. In addition to the maximum SCF given by Equation (63), it is also possible to write the equation for the minimum SCF:

$$K_{\text{T},\text{MIN}}^{\infty }==\frac{{\sigma }_x(\mathrm{0,}r)}{\overline{\sigma }}=\overline{\sigma }\mathrm{Re}\left[{\mu }_1{\mu }_2\right].$$ (64)

Consider a symmetrical laminate of graphite/epoxy with elastic properties given in Table 2. Plate dimensions are much larger than the hole diameter, so a uniform uniaxial stress-tension region completely surrounds the hole. Due to the symmetry of the problem, the modeling can be performed considering the geometry shown in Figure 7 with the specified dimensions, which is the representation of a quarter of the model shown in Figure 6. The geometry was built with NURBS of degree $p=2$ with unidirectional fiber reinforced lamina with fiber angles varying at $\theta =(0^{°}{\mathrm{,45}}^{°}{\mathrm{,90}}^{°})$. In Figure 7 is shown point A where the maximum stress occurs and point B where the minimum stress occurs. Finally, to obtain the numerical solution, the boundary conditions given by equation (65) are considered.

Table 2
Elastic properties graphite/epoxy.

Description of variables	Values of variables
Longitudinal elastic modulus	$E_1=181\text{GPa}$
Transverse elastic modulus	$E_2=10.3\text{GPa}$
Poisson's coefficient	${\nu }_{12}=0.28$
Shear module	$G_{12}=7.17\text{GPa}$
Load	$\overline{\sigma }=1$

Figure 7
Illustration of a quarter of the plate with the hole pulled in the $y$ direction.

Table 3 shows the numerical results for the maximum SCF (point A of Figure 7) and the minimum SCF (point B of Figure 7). In the analysis of three laminate fiber directions, results are in good agreement when compared to analytical solutions, as can be seen through the percent error shown in the table, and also with quadratic discontinuous boundary element method (shape functions are Lagrangian polynomials).

Table 3
Numerical results for SCF maximum (point A) and SCF minimum (point B) shown in Figure 7.

SCF maximum and minimum (IGABEM)					SCF maximum and minimum (Lagrangian BEM)
	$\theta =0^{\circ }$	$\theta =45^{\circ }$	$\theta =90^{\circ }$			$\theta =0^{\circ }$	$\theta =45^{\circ }$	$\theta =90^{\circ }$
Total collocation nodes	85	120	315		Total collocation nodes	100	140	1000
Percent error	0.01%	0.26%	0.18%		Percent error	0.16%	0.31%	4.08%
IGABEM	2.37144	2.37409	6.73794		Lagrangian BEM	2.37557	2.37918	6.47457
Analytical	2.37177	2.38043	6.75048		Analytical	2.37177	2.38043	6.75048
Total collocation nodes	200	100	140		Total collocation nodes	1000	140	160
Percent error	0.12%	0.91%	0.03%		Percent error	1.54%	0.96%	0.07%
IGABEM	-4.19743	-0.52409	-0.23863		Lagrangian BEM	-4.12714	-0.52380	-0.23873
Analytical	-4.19199	-0.52892	-0.23855		Analytical	-4.19199	-0.52892	-0.23855

$$\text{bc:}\left\{\begin{array}{l}{t}_x=u_y=\mathrm{0,}(x,y)\in N_1,\\ \\ t_x=t_y=\mathrm{0,}(x,y)\in N_2,\\ \\ t_x=\mathrm{0,}{t}_y=\overline{\sigma },(x,y)\in N_3,\\ \\ u_x=t_y=\mathrm{0,}(x,y)\in N_4,\\ \\ t_x=t_y=\mathrm{0,}(x,y)\in N_5.\end{array}\right.$$ (65)

Figure 8 shows displacements for the infinite plates for the three analyzed cases. The black line is the undeformed plate, and the blue line is the deformed plate.

Figure 8
Original plate (black) and deformed (blue) with fiber orientations in (a) $\theta =0^{°}$, (b) $\theta ={45}^{°}$and (c) $\theta ={90}^{°}$.

5.3 Stress distributions along the main direction.

The analytical solution for the distribution of stresses along the principal direction of a circular hole in an orthotropic plate of infinite dimensions was presented by Lekhnitskii (1968). For the same problem, in Nuismer and Whitney (1975) we see a regression polynomial obtained by adding second, fourth, sixth and eighth order terms, which very well simulates the Lekhnitskii analytical solution. Terms of this polynomial were determined from the use of the exact value of the SCF given by Equation (62) for the orthotopic case or by Equation (63) for the anisotropic case. The polynomial equation is written as:

$${\sigma }_y(x\mathrm{,0})=\frac{\overline{\sigma }}{2}\left\{2+{\left(\frac{r}{x}\right)}^2+3{\left(\frac{r}{x}\right)}^4-\left(K_{T,\text{MAX}}^{\infty }-3\right)\left[5{\left(\frac{r}{x}\right)}^6-7{\left(\frac{r}{x}\right)}^8\right]\right\},x>r,$$ (66)

For applications in this section, geometric configurations similar to those applied in the problem presented in section 5.2, see Figure 9, are considered, but with radius $r=1$, width of the plate $x=30$, and the height of the plate $y=30$. The boundary conditions are the same as shown in Equation (65). The laminate considered in this application is a cross-ply laminate with stacking sequence ${\left[0/90\right]}_S$. Numerical results were obtained based on three types of symmetrical laminates: graphite/epoxy, boron/epoxy, and aramid/epoxy as shown in Table 4.

Figure 9
Illustration of the collocation points for a quarter of the plate with a hole pulled in the $y$ direction.

Table 4
Elastic properties for laminated materials.

Graphite / Epoxy (AS / 3501)		Boron / Epoxy (B(4) / 5505)		Aramid / Epoxy (kevlar 49/epoxy)
Description of variables	Values of variables	Description of variables	Values of variables	Description of variables	Values of variables
$E_1$	$138\text{GPa}$	$E_1$	$\text{204 GPa}$	$E_1$	$76\text{GPa}$
$E_2$	$8.96\text{GPa}$	$E_2$	$18.8\text{GPa}$	$E_2$	$5.5\text{GPa}$
$G_{12}$	$\text{7}\text{.1 GPa}$	$G_{12}$	$\text{5}\text{.59 GPa}$	$G_{12}$	$\text{2}\text{.3 GPa}$
${\nu }_{12}$	$0.30$	${\nu }_{12}$	$0.23$	${\nu }_{12}$	$0.34$

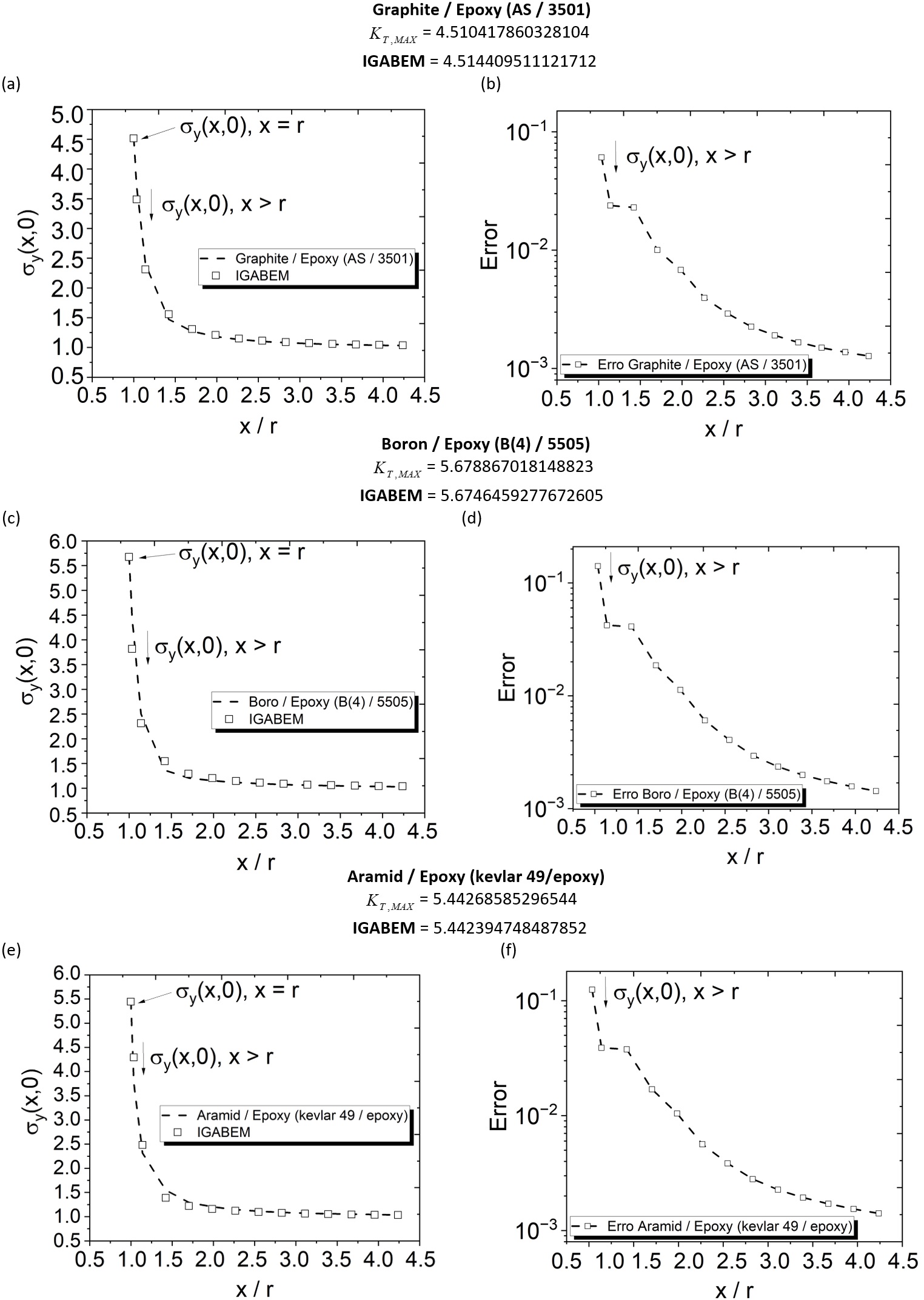
Figure 10 shows the numerical results for ${\sigma }_y(x\mathrm{,0})$ for the three types of materials. A total of 105 collocation points with 8 control points were used. For plotting the graphs, only the values in ${\sigma }_y(\mathrm{1,0})$ are shown where the SCF is located, and the other ${\sigma }_y(x\mathrm{,0})$, for $1<x<\mathrm{4,5}$. Numerical results, as shown in Figure 10 (a), (c), and (e), show a good agreement for the given materials. However, in Konish & Whitney (1975), authors point out that this solution is restricted to geometries where the plate dimensions are much larger with respect to the hole size.

Figure 10
Stress distribution for: (a) graphite/epoxy, (c) boron/epoxy and (e) aramid/epoxy, and their respective errors.

To measure the magnitude of the errors between the analytical and the numerical solution, errors are plotted for each type of material, as shown in Figures 10 (b), (d), and (f). This error analysis was performed using Equation (67).

$$\text{Error}=\frac{\left|\underset{analytical}{\underbrace{u_i}}-\underset{numerical}{\underbrace{\overline{u_i}}}\right|}{\text{MAX}\left|\underset{analytical}{\underbrace{u_i}}\right|},\text{for}i=\mathrm{1,2,}\dots n.$$ (67)

As it can be seen in Figure 10, the behavior of errors is as expected, i.e., they are larger near the hole, decreasing with the increase of the distance from the hole.

5.4 Tangential stress distributions along the circumference of the hole.

This application is based on a geometry similar to the problem in Figure 6, being the plate of infinite dimensions with a circular hole. However, now the stress $\overline{\sigma }$ is applied in the $x$ direction, as shown in Figure 11. Note that in this application an angle $\phi$is considered, which describes the direction of the fiber in the laminate. Notice that the maximum SCF is now located at point B and the minimum SCF at point A. Thus, the analytical equation for the tangential stress a the hole ${\sigma }_{\theta }$ in Figure 11 is given as:

Figure 11
Hole in infinite plane and uniform stress in $x$, being $(x´,y´)$ the coordinates of the fibers and $(x,y)$ of the laminate.

$${\sigma }_{\theta }=\overline{\sigma }\frac{E_{\theta }}{E_1}\left\{\left[-{\cos }^2\phi +(k+n){\sin }^2\phi \right]k{\cos }^2\theta +\left[(1+n){\cos }^2\phi -k{\sin }^2\phi \right]{\sin }^2\theta -n(1+k+n)\sin \phi \cos \phi \sin \theta \cos \theta \right\}.$$ (68)

Constants $k$and $n$ are given by Lekhnitskii (1968). Note that $\theta$ is the polar angle measured from the $x$ axis and $E_{\theta }$ is the Young's modulus in the tangent direction to the opening boundary written according to Equation (69), which is related to the elastic constants in the principal direction by:

$$E_{\theta }={\left\{\frac{{\sin }^4\theta }{E_1}+\left(\frac{1}{G}-\frac{2v_1}{E_1}\right){\sin }^2\theta {\cos }^2\theta +\frac{{\cos }^4\theta }{E_2}\right\}}^{-1}.$$ (69)

For computational simulation of this problem, consider the geometry shown in Figure 12 given by five NURBS curves. Information on material type, source points, control points and NURBS degree are detailed in Tables 5, 6, and 7. Boundary conditions necessary for the numerical solution of the problem are given in Equation (70).

Figure 12
Illustration of a quarter of the plate with a hole pulled in the $x$ direction.

Table 5
NURBS data and elastic properties for boron/aluminum (B4/6061-Al) laminate.

Boron / Aluminium (B4/6061-Al)		Elastic properties
Source points	$30$	$E_1$	$\text{235 GPa}$	$G_{12}$	$\text{47 GPa}$
Control points	$\text{08}$	$E_2$	$137\text{GPa}$	${\nu }_{12}$	$0.30$
NURBS degree	$\text{04}$

Table 6
NURBS data and elastic properties for carbon/epoxy (AGP370-5H/3501-6S) laminate.

Carbon / Epoxy (AGP/370-5H/350-6S)		Elastic properties
Source points	$30$	$E_1$	$\text{77 GPa}$	$G_{12}$	$\text{6}\text{.5 GPa}$
Control points	$\text{08}$	$E_2$	$75\text{GPa}$	${\nu }_{12}$	$0.06$
NURBS degree	$\text{04}$

Table 7
NURBS data and elastic properties for carbon / phenolic (8H Fabric) laminate.

Carbon / Phenolic (8H Fabric)		Elastic properties
Source points	$30$	$E_1$	$\text{20 GPa}$	$G_{12}$	$\text{6}\text{.8 GPa}$
Control points	$\text{08}$	$E_2$	$19\text{GPa}$	${\nu }_{12}$	$0.23$
NURBS degree	$\text{04}$

$$\text{Boundary conditions:}\left\{\begin{array}{l}{t}_x=u_y=\mathrm{0,}(x,y)\in N_1,\\ \\ t_x=\overline{\sigma },t_y=\mathrm{0,}(x,y)\in N_2,\\ \\ t_x=t_y=\mathrm{0,}(x,y)\in N_3,\\ \\ u_x=t_y=\mathrm{0,}(x,y)\in N_4,\\ \\ t_x=t_y=\mathrm{0,}(x,y)\in N_5.\end{array}\right.$$ (70)

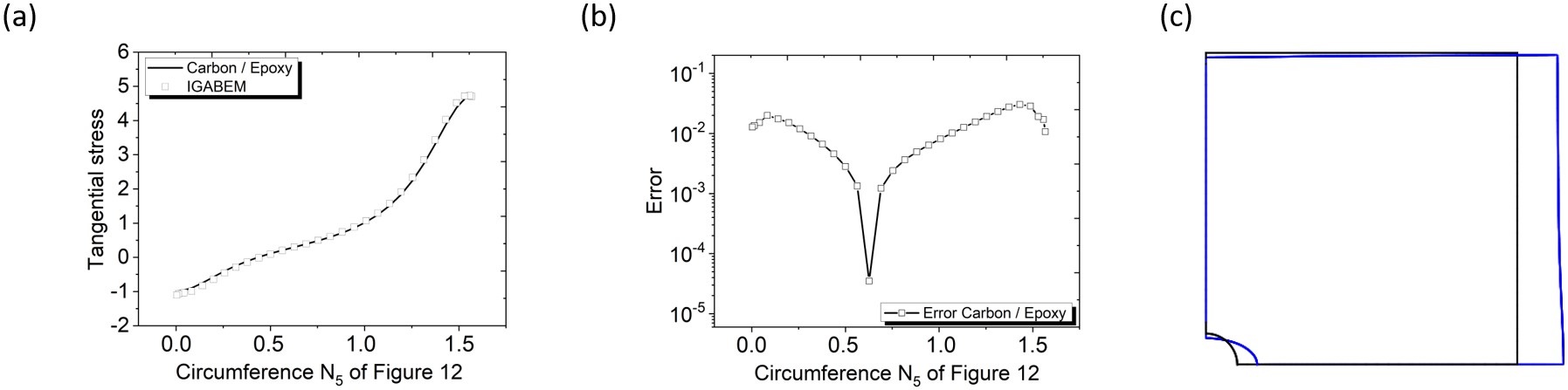
In these examples, boron/aluminium, carbon/epoxy and carbon/phenolic laminates are used, whose elastic constants were taken from Daniel et al., (2006). Figures 13(a), 14(a), and 15(a) show different variations of tangential stresses around the circumference of the circular hole for the laminates. Whereas, the errors shown in Figures 13(b), 14(b) and 15(b) were obtained through Equation (67). Furthermore, in Figures 13(c), 14(c), and 15(c) the deformations of each laminate are shown.

Figure 13
Boron/Aluminum: (a) tangential stresses in ${\sigma }_{\theta }$ (b) error, and (c) deformation.

Figure 14
Carbon/Epoxy: (a) tangential stresses in ${\sigma }_{\theta }$ (b) error, and (c) deformation.

Figure 15
carbon / phenolic: (a) tangential stresses in ${\sigma }_{\theta }$ (b) error, and (c) deformation.

All numerical results for the different laminates given in Figures 13 - 15 show good agreement with the analytical solution. However, it is worth mentioning two situations that we must be aware when simulating this type of problem. The first is the degree of anisotropy $E_1/E_2$, which when it is large, it can increase the difficulty of the numerical results to agree to the analytical ones, as the anisotropic degree larger in Figure 13 with respect to that used in Figure 15, for example. And the second situation is that in the regions close to the hole, the numerical results always present a little more difficulty in following the analytical solution as well, as shown in the error analysis of Figures 15, for example. This can be justified, because close to the boundaries there are sudden variations of the stress.

6 CONCLUSION

In this paper, the IGABEM with Bézier decomposition was successfully applied to solve 2D anisotropic plane elastic problems. The Lekhnitskii's anisotropic fundamental solution was used and the singular integral terms, which arise in the boundary integral equation of displacement and traction, were regularized. For the weak singularity kernel, the Telles transformation was used. For the strong singularity term, the singularity subtraction technique was used. The convergence and numerical precision of the proposed formulation was demonstrated through the analysis of different problems. Stress distribution in a rotating disk was computed by a different approach, using modified boundary conditions. Numerical solutions computed using IGABEM have shown excellent agreement with analytical solutions available in the literature, even with a small amount of degrees of freedom.

Acknowledgements

The first author of this work thanks the Federal University of West Bahia for the license granted for his doctoral studies at the University of Brasília.

References

• Albuquerque, E. L., Sollero, P., & Aliabadi, M. H. (2004). Dual boundary element method for anisotropic dynamic fracture mechanics. International Journal for Numerical Methods in Engineering, 59(9), 1187-1205.
• Beer, G., & Duenser, C. (2019). Isogeometric boundary element analysis of problems in potential flow. Computer Methods in Applied Mechanics and Engineering, 347, 517-532.
• Beer, G., Marussig, B., & Duenser, C. (2020). The isogeometric boundary element method. Heidelberg: Springer.
• Borden, M. J., Scott, M. A., Evans, J. A., & Hughes, T. J. (2011). Isogeometric finite element data structures based on Bézier extraction of NURBS. International Journal for Numerical Methods in Engineering, 87(1‐5), 15-47.
• Cabral, J. J. S. P., Wrobel, L. C., & Brebbia, C. A. (1990). A BEM formulation using B-splines: I-uniform blending functions. Engineering analysis with boundary elements, 7(3), 136-144.
• Caicedo, J., & Portela, A. (2017). Direct computation of stress intensity factors in finite element method. European Journal of Computational Mechanics, 26(3), 309-335.
• Chang, C. I. (1974). A closed-form solution for an orthotropic rotating disk. Journal of Applied Mechanics. 41(4): 1122-1123.
• Cordeiro, S. G. F., & Leonel, E. D. (2020). Subtraction singularity technique applied to the regularization of singular and hypersingular integrals in high-order curved boundary elements in plane anisotropic elasticity. Engineering Analysis with Boundary Elements, 119, 214-224.
• Cottrell, J. A., Hughes, T. J., & Bazilevs, Y. (2009). Isogeometric analysis: toward integration of CAD and FEA. John Wiley & Sons.
• Daniel, I. M., Ishai, O., Daniel, I. M., & Daniel, I. (2006). Engineering mechanics of composite materials (Vol. 1994). New York: Oxford University Press.
• Deb, A., & Banerjee, P. (1990). BEM for general anisotropic 2D elasticity using particular integrals. Communications in Applied Numerical Methods, 6(2), 111-119.
• Gaul, L., Kögl, M., & Wagner, M. (2013). Boundary element methods for engineers and scientists: an introductory course with advanced topics. Springer Science & Business Media.
• Guiggiani, M. (1998). Formulation and numerical treatment of boundary integral equations with hypersingular kernels. Singular integrals in boundary element methods, 10, 85-124.
• Hughes, T. J., Cottrell, J. A., & Bazilevs, Y. (2005). Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39-41), 4135-4195.
• Hwu, C. (2010). Anisotropic elastic plates. Springer Science & Business Media.
• Konish, H. J., & Whitney, J. M. (1975). Approximate stresses in an orthotropic plate containing a circular hole. Journal of Composite Materials, 9(2), 157-166.
• Lekhnitskii, S. G. (1968). Anisotropic plates. Foreign Technology Div Wright-Patterson Afb Oh.
• Li, K., & Qian, X. (2011). Isogeometric analysis and shape optimization via boundary integral. Computer-Aided Design, 43(11), 1427-1437.
• Marczak, R. J., & Creus, G. J. (2002). Direct evaluation of singular integrals in boundary element analysis of thick plates. Engineering Analysis with Boundary Elements, 26(8), 653-665.
• Nuismer, R. J., & Whitney, J. M. (1975). Uniaxial failure of composite laminates containing stress concentrations (pp. 117-142). ASTM International.
• Oliveira, T., & Portela, A. (2019). A local mesh free method with the singularity subtraction technique. Engineering Analysis with Boundary Elements, 104, 148-159.
• Özaslan, E., Yetgin, A., & Acar, B. (2019). Stress concentration and strength prediction of 2× 2 twill weave fabric composite with a circular hole. Journal of Composite Materials, 53(4), 463-474.
• Pastorino, D., Blázquez, A., López-Romano, B., & París, F. (2021). Closed-form methodology for the bending of symmetric composite plates with cutouts and non-uniform lay-up. Composite Structures, 271, 114052.
• Rajapakse, R. K. N. D., & Xu, X. L. (2001). Boundary element modeling of cracks in piezoelectric solids. Engineering Analysis with Boundary Elements, 25(9), 771-781.
• Simpson, R. N., Bordas, S. P., Lian, H., & Trevelyan, J. (2013). An isogeometric boundary element method for elastostatic analysis: 2D implementation aspects. Computers & Structures, 118, 2-12.
• Sollero, P., & Aliabadi, M. H. (1993). Fracture mechanics analysis of anisotropic plates by the boundary element method. International Journal of Fracture, 64(4), 269-284.
• Telles, J. (1987). A self‐adaptive co‐ordinate transformation for efficient numerical evaluation of general boundary element integrals. International Journal for Numerical Methods in Engineering, 24(5), 959-973.
• Wang, Y. J., & Benson, D. (2015). Multi-patch nonsingular isogeometric boundary element analysis in 3D. Computer Methods in Applied Mechanics and Engineering, 293, 71-91.

Edited by

• Editor: Rogério José Marczak

Publication Dates

• Publication in this collection
  09 Jan 2023
• Date of issue
  2023

History

• Received
  12 Sept 2022
• Reviewed
  14 Nov 2022
• Accepted
  07 Dec 2022
• Published
  08 Dec 2022