Buckling of Axially Compressed Conical Shells with Multiple Imperfections

Abstract

The influence of single and multiple imperfection cases on the load carrying capacity of mild steel cone subjected to axial compression was considered through numerical simulation in the current paper. Three different imperfection techniques were considered, which are: i) uneven axial length (sinusoidal/square waves), ii) crack, and iii) single load indentation (SLI) imperfection. Abaqus 6.19 FE was used to carry out the numerical simulation. The axial compressive load was applied at the small radius of the cone. Results showed that the buckling load of axially compressed mild steel cone depends on the imperfection approach implemented. The buckling load of cones were seen to be heavily affected by uneven axial length imperfection for both single and multiple imperfection. Also, the effect of multiple imperfection is more noticeable at higher r₁/t.

Keywords:
Multiple imperfections; axial compression; steel cone; buckling; Finite Element Analysis

Graphical Abstract

1 INTRODUCTION

The presence of imperfection has long been acknowledged to have a significant influence on the reduction of the buckling load of thin-walled conical shell structures. It is usually inevitable owing to the manufacturing process or unforeseeable damage (Dinkler and Knoke 2003). Several types of well-known imperfection includes the non-uniformity in the material’s physical properties, geometric imperfections (Mahidan and Ifayefunmi 2020a; Ifayefunmi and Mahidan 2021; Khakimova et al. 2014; Özyurt et al. 2017), load eccentricities (Castro et al. 2014), boundary conditions irregularities (Ifayefunmi et al. 2018), crack imperfection (Ifayefunmi 2020; Ifayefunmi and Mahidan 2020; Cui and Shao 2015; Ali 2013), material discontinuity (Ifayefunmi and Ibrahim 2018; Ifayefunmi 2017), etc. To date, there is a vast amount of literatures that can be found concentrating on the effect of geometric imperfection on the buckling behaviour of certain structures such as conical and cylindrical shells. Ifayefunmi (2014) and Ifayefunmi and Błachut (2018) reviewed the conical shells’ sensitivity towards imperfection. While the influence of imperfections in shell finite element collapse simulations has long been the subject of research, only a few literatures exist on modelling their combined effect.

Buckling behaviour of composite conical shells subjected to axial compression was studied through the combination of dent and initial non-uniformity (i.e., mid-surface imperfection, MSI and thickness imperfection, TI) by Khakimova et al. (2014). The dent was simulated through Single Perturbation Load Approach (SPLA), whereas the measured thickness imperfection was mapped to the 45° conical model. The lowest load carrying capacity was recorded by conical shells with SPLA and TI. This was followed by the combination of SPLA + MSI + TI, SPLA only, and lastly, SPLA + MSI. However, the results lead to the conclusion that the effect of MSI and TI is marginal because the percentage difference between the SPLA only and the combined imperfection is only -2% to 1%.

Hafeez et al. (2010) studied the stability of combined imperfections on combined conical shells, with an upper cylindrical cap under hydrostatic loading. The study addressed the impact of residual stresses as the result of the welding process and/or geometric imperfection on the combined conical tanks’ buckling performance through numerical simulations. The load carrying capacity of the perfect combined conical tanks was reduced by about 8.6% to 29.5% due to the influence of residual stress. In contrast, geometric imperfection plays a more prominent role in the reduction of the conical tank’s loading capacity where 32.4% to 45.2% reduction were recorded. Ultimately, the combination of residual stresses and geometric imperfection causes the maximum buckling load reduction for this type of structure ranging from 40.3% to 48.6%. Some of the earliest literatures on the influence of residual stresses due to circumferential welding on cylindrical shells can be found in Bornscheuer and Hafner (1983) and Rotter (1996). Alvarenga and Silveira (2009) covers the effect of the combination of residual stress and geometric imperfection in terms of structure’s out-of plumbness and members’ out-of-straightness imperfections on steel columns.

From the literature survey, there is a significant gap to be filled in on the subject of the influence of multiple imperfections on the buckling behaviour of conical shells. This paper addressed the problem through the combination of i) single load indentation (SLI) + crack, ii) SLI + uneven axial length, and iii) crack + uneven axial length on mild steel conical shells when subjected to axial compression. This research is entirely based on numerical computation.

2 BUCKLING OF PERFECT CONICAL SHELL SUBJECTED TO AXIAL COMPRESSION

2.1 Modelling of the perfect conical shell

Assume a conical shell with the following geometry: r₂/r₁ = 2.0; r₁/t = 25; L/r₂ = 2.24; β = 12.6°; wall thickness = 1 mm, as sketched in Figure 1. Cone was characterized as a deformable part with four-node shell elements and six-degree of freedom (S4R) and has had the boundary condition set up as detailed in Table 1. These physical properties of the cone will be implemented throughout this paper. In addition to that, a rigid plate was created at the top of the cone. The modelled mild steel cones have the material properties as stated in Table 2. Contact interaction for the cone was modelled as surface-to-surface interaction between the internal surface of the rigid plate and the top nodes of the cone through the master-slave algorithm and is assumed to have a frictionless tangential behavior. The rigid plate was assigned as the master while the node located at the cone’s top was assigned as the slave. Then, the conical model was axially compressed through non-linear static Riks load step.

Figure 1
Geometry of the cone.

Table 1
The boundary condition of the numerical model (Note: 0 ≡ fixed; 1 ≡ free).

Position	Displacements			Rotations
	ux	uy	uz	ϕx	ϕy	ϕz
Top edge of cone	0	1	0	0	0	0
Bottom edge of cone	0	0	0	0	0	0
Compression plate	0	1	0	0	0	0

Table 2
Mechanical properties of mild steel as referred to Mahidan and Ifayefunmi (2020a).

Young’s modulus, E (GPa)	Yield stress, σyp (MPa)	Poisson’s ratio, υ	Wall thickness, t (mm)
168.791	229.774	0.3	1

2.2 Mesh convergence study

Figure 2 illustrates the result of different mesh element size on the buckling load of a perfect conical shell subjected to axial compression. It can be seen that at 1872 element size, the perfect cone’s buckling load started to converge. Hence, the numerical modelling in this study was conducted using this element size. The finite element analysis for the problem as mentioned above was executed using the Abaqus finite element (FE) code (Smith 2009).

Figure 2
Plot of the buckling load of a perfect cone with r₁/t = 25 against different size of element in the Abaqus.

2.2 Modelling of imperfect conical shells

2.3.1 Single load indentation (SLI) imperfection

Load indentation (PL) was created at the mid-axial length of the cone through the static general load algorithm as shown in Figure 3(a). This loading step will initiate a dent having a certain imperfection amplitude, A, (ranging from 0.28 mm to 2.8 mm). Two distinct steps were involved in running the analysis, they are: i) static general procedure in which the dent was simulated, and ii) non-linear static Riks in which the axial loading was applied on a reference point located at the center of the top plate (Figure 3).

2.3.2 Crack imperfection

Circumferential crack (θ = 0° corresponds to circumferential direction as measured from the cone circumferential line) was simulated on the conical model having various imperfection amplitude (i.e., crack length), A, ranging from 0.28 to 2.80. The crack was located at the mid-section of the cone as depicted in Figure 3(b). During the cone modelling in Abaqus, the mesh-zooming scheme proposed in Estekanchi and Vafai (1999) was implemented - mesh size is finer at the crack region in comparison to the uncracked region of the cone. The numerical FEA has been benchmarked against the numerical data presented in Jahromi and Vaziri (2012) and the result can be found in Ifayefunmi and Mahidan (2020). The percentage difference between Jahromi and Vaziri (2012) and Ifayefunmi and Mahidan (2020) is from 0.99 to 1.01. Thus, the appropriateness of the above numerical scheme is proven. Then, the cone is subjected to axial compression through non-linear static Riks analysis.

2.3.3 Uneven axial length imperfection

Deformable conical shell with axial length imperfection in the form of sinusoidal or square waves were modelled in Abaqus. The number of waves, N is equal to 2. The waves were introduced at the top edge of the cone (see Figure 3(c)) where the axial compression will occur owing to the fact that the plastic strain was claimed to be concentrated within the chosen area (Błachut 2010; Błachut and Ifayefunmi 2010; Błachut et al. 2011; Mahidan and Ifayefunmi 2021). Again, the compression load was applied on the top of the cone through a non-linear static Riks load step.

2.3.4 Multiple imperfections

In this paper, the results of multiple imperfection were achieved by combining two different types of imperfection on a cone. The multiple imperfection cases comprise of the following combinations: i) SLI + crack, ii) SLI + uneven axial length and, iii) uneven axial length + crack. The imperfections were located opposite to each other at the mid-length of the deformable cone (for the case of crack + SLI imperfection) before the model was axially compressed through the non-linear static Riks analysis.

Figure 3
Geometry of imperfect cones with the presence of (a) SLI, (b) crack, and (c) uneven axial length imperfections - sinusoidal waves.

3 RESULTS AND DISCUSSION

3.1 Imperfection sensitivity of axially compressed conical shell having single or multiple imperfections

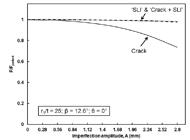
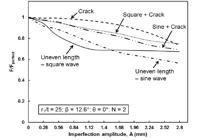
The study addressed the effect of single (SLI, crack, and uneven axial length) and combined imperfection (SLI + crack, SLI + uneven axial length, and uneven axial length + crack) on the load bearing capacity of the cones. The buckling load of each single and/or combined imperfection can be found in Table 3, for conical shells with top radius-to-thickness ratio, r₁/t = 25. It can be seen that the cone with uneven axial length imperfection generally have has the worst buckling load in comparison to other single imperfection cases. For instance, at A = 0.28, the buckling load of the imperfect cone drop to about 91.8% from the perfect one (refer column 3 of Table 3). When imperfection amplitude was further increased to 2.80, the cone reduces to 56.1% from its perfect counterpart. This was then followed by crack, and SLI imperfection being the least imperfection sensitive. Whereas, for the case of combined imperfection, it was observed that when imperfection amplitude, A ≤ 1.12, the combination of sinusoidal wave + SLI imperfection produced the lowest load carrying capacity compared to other combined imperfection. While, the combination of crack + SLI imperfection seems to have the least effect on the collapse force of cones under axial compression for the range of imperfection amplitude considered in this study (i.e., 0 - 2.80) - as summarized in column 10 of Table 3. However, as the imperfection amplitude continuously raised to 2.80, cones with sinusoidal wave + crack imperfection recorded the worst buckling load (column 7, row 8 of Table 3).

Again, from Table 3, it is obvious that the uneven axial length imperfection possesses a significant impact in determining the collapse force of conical structures subjected to axial compression. This particular imperfection type predicted the highest reduction of buckling load on its own, and when in combination with other types of imperfection, it resulted in a notable decrease in the conical shells’ collapse load. Figures 4, 5 and 6 show the comparison in terms of buckling load for single and combined imperfections. The buckling load is normalized by the perfect cone’s buckling load, F/F_perfect.

Table 3
Collapse load (kN) of conical shells having single/combined imperfection with r₁/t = 25.

A	Single Imperfection				Multiple Imperfection
	Uneven length		Crack	SLI	Uneven length				Crack + SLI
	Square wave	Sine wave			Square + Crack	Sine + Crack	Square + SLI	Sine + SLI
0	37.85	37.85	37.85	37.85	37.85	37.85	37.85	37.85	37.85
0.28	35.62	34.73	37.60	37.94	36.76	36.92	36.86	36.57	37.94
0.56	31.02	33.44	37.59	37.93	35.89	36.15	35.56	35.57	37.88
1.12	26.49	29.14	36.73	37.73	33.72	33.10	33.06	32.85	37.76
1.68	26.02	25.22	35.13	37.55	31.96	30.95	31.16	31.16	37.64
2.24	25.81	23.29	32.20	37.40	29.48	27.83	29.94	28.32	37.45
2.80	25.51	21.25	27.84	37.24	28.27	26.15	29.48	26.79	37.01

Figure 4
The normalized buckling load of perfect and imperfect cones with crack, SLI and crack + SLI imperfection at different imperfection amplitude, A (r₁/t = 25).

Figure 5
The normalized buckling load of perfect and imperfect cones with uneven axial length, SLI and uneven axial length + SLI imperfection at different imperfection amplitude, A (r₁/t = 25).

Figure 6
The normalized buckling load of perfect and imperfect cones with uneven axial length, crack and uneven axial length + crack imperfection at different imperfection amplitude, A (r₁/t = 25).

3.2 Influence of different top radius-to-thickness ratio, r₁/t

Next, the study explores the effect of different r₁/t in the range of 25 - 2000 to the axial collapse force of the conical shells. It must be noted that the top radius of the cone remains constant for all range of r₁/t tested in this paper. Furthermore, because of different r₁/t, the imperfection amplitude, A, considered in this section is 0 < A ≤ 0.56. For smaller radius-to-thickness ratio (r₁/t ≤ 250) - typically found in offshore structures, the buckling was seen to be governed by elastic-plastic buckling. In contrast, for relatively thin wall thickness represented by r₁/t = 2000 has its buckling governed by elastic buckling. Non-linear static Riks step was used in the Abaqus for plastic analysis, while buckle step was implemented for elastic analysis.

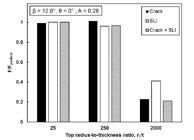
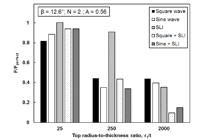
The buckling load of the axially compressed conical shells having different r₁/t was summarized in Table 4. From Table 4, it can be seen that the buckling load of perfect and imperfect conical shell reduces as the r₁/t increases. As an example, imperfect cone with uneven axial length in the form of sinusoidal wave with an imperfection amplitude, A = 0.28 experienced the reduction in the ratio of imperfect-to-perfect buckling load from 92% to 42% when the r₁/t was increased from 25 to 250. The same can be said for the case of the combined imperfection of sinusoidal waves + SLI with A = 0.56, where the cone experienced the reduction in the ratio of imperfect-to-perfect buckling load from 94% to 34% when the r₁/t was increased from 25 to 250.

Again, conical shell with uneven axial length (sinusoidal waves) shows the highest reduction of load carrying capacity for the case of single imperfection at r₁/t ≤ 250 (column 4 of Table 4) for both imperfection amplitudes considered in Table 4. However, at r₁/t = 2000, conical shell with crack imperfection records the lowest buckling load, where 25% and 17% reduction of buckling load from the perfect one was noticed for A = 0.28 and 0.56, respectively. Further, for the case of multiple imperfections, the combination of uneven axial length (sinusoidal waves) & crack imperfection showed the highest sensitivity to imperfection for r₁/t =250, as seen in column 8 of Table 4. This could be the result of the worst buckling load produced by the sinusoidal wave in the single imperfection earlier. At r₁/t = 2000 and A = 0.56, as expected, the combination of crack & SLI imperfection yielded the worst buckling load, similar to their equivalent in the single imperfection columns. Although, the same cannot be said for A = 0.28. Figures 7, 8 and 9 illustrate the buckling load of conical shells for different r₁/t with single and combined imperfection cases having imperfection amplitude, A = 0.28. Whilst, the load carrying capacity of conical shells for different r₁/t with single and combined imperfection cases having imperfection amplitude, A = 0.56 can be seen in Figures 10, 11 and 12.

In general, it can be seen that the SLI imperfection has little influence on the buckling load of both single and combined imperfection cases. This observation is somewhat similar to the one presented in Khakimova et al., (2014). Then, the effect of combined imperfection cases was more noticeable as the r₁/t of the cone was increased. For example, at r₁/t = 25, the single imperfection of uneven axial length in the form of sinusoidal wave yielded the worst collapse force. However, it can be seen from Table 4 that the combination of sinusoidal wave and crack imperfections was the worst for r₁/t = 250, while the combination of square wave and SLI imperfections was the worst for r₁/t = 2000. Ultimately, it can be concluded that the uneven axial length imperfection has a substantial impact on the reduction of buckling load of axially compressed conical shells.

Table 4
Collapse load (kN) of conical shells having single/combined imperfection with different r₁/t.

r1/t	A	Single imperfection				Multiple imperfection
		Uneven length		Crack	SLI	Uneven length				Crack + SLI
		Square wave	Sine wave			Square + Crack	Sine + Crack	Square + SLI	Sine + SLI
25	0	37.85	37.85	37.85	37.85	37.85	37.85	37.85	37.85	37.85
	0.28	35.62	34.73	37.60	37.94	36.76	36.92	36.86	36.57	37.94
	0.56	31.02	33.44	37.59	37.93	35.89	36.15	35.56	35.57	37.88
250	0	3.54	3.54	3.54	3.54	3.54	3.54	3.54	3.54	3.54
	0.28	2.01	1.47	3.59	3.41	1.57	1.42	1.77	1.48	3.43
	0.56	1.57	1.24	3.59	3.22	1.55	1.13	1.55	1.20	2.83
2000	0	0.12	0.12	0.12	0.12	0.12	0.12	0.12	0.12	0.12
	0.28	0.05	0.06	0.03	0.05	0.06	0.06	0.02	0.03	0.03
	0.56	0.05	0.05	0.02	0.04	0.06	0.06	0.01	0.02	0.01

Figure 7
Influence of different r₁/t to the buckling load of axially compressed cones with crack, SLI, and crack + SLI imperfection for A = 0.28.

Figure 8
Influence of different r₁/t to the buckling load of axially compressed cones with uneven axial length, SLI and uneven axial length + SLI imperfection for A = 0.28.

Figure 9
Influence of different r₁/t to the buckling load of axially compressed cones with uneven axial length, crack and uneven axial length + crack imperfection for A = 0.28.

Figure 10
Influence of different r₁/t to the buckling load of axially compressed cones with crack, SLI, and crack + SLI imperfection for A = 0.56.

Figure 11
Influence of different r₁/t to the buckling load of axially compressed cones with crack, SLI, and crack + SLI imperfection for A = 0.56.

Figure 12
Influence of different r₁/t to the buckling load of axially compressed cones with uneven axial length, crack and uneven axial length + crack imperfection for A = 0.56.

4 CONCLUSION

Finite element predictions on the buckling behaviour of axially compressed conical shells with single and multiple imperfection were presented in this paper. First, the paper compares the effect of single and multiple imperfection on the conical shells having top radius-to-thickness ratio, r₁/t of 25. Whilst, the influence of different r₁/t was addressed in the subsequent section where the r₁/t was increased up to 2000. Several conclusions can be produced from the preceding results: i) the uneven axial length imperfection can cause more damage to the structure’s load carrying capacity than the combined imperfection cases when the r₁/t = 25, ii) SLI imperfection has a minimal impact on the buckling behaviour of axially compressed cones, iii) the presence of uneven axial length imperfection in the combined imperfection cases caused a substantial decrease in the conical shells’ load bearing capacity, iv) the conical shells’ sensitivity to imperfection depends on the imperfection approach implemented during study, and lastly, v) cones with multiple imperfection starts to produce lower buckling load than cones with single imperfection as the r₁/t was increased.

References

• Ali, D. (2013). Buckling of cracked conical frusta under axial compression. Research Journal of Recent Sciences 2(2):33-39.
• Alvarenga, A.R., and Silveira, R.A.M. (2009). Second-order plastic-zone analysis of steel frames - Part II: effects of initial geometric imperfection and residual stress. Latin American Journal of Solids and Structures, 6:323-342.
• Błachut, J. (2010). Buckling of axially compressed cylinders with imperfect length. Computers and Structures, 88(5-6):365-374. https://doi.org/10.1016/j.compstruc.2009.11.010.
  » https://doi.org/10.1016/j.compstruc.2009.11.010.
• [Q1: Q1]]Błachut, J., and Ifayefunmi, O. (2010). Buckling of unstiffened steel cones subjected to axial compression and external pressure. Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2010), Vol. 2, OMAE2010-20518. New York, USA, 385-398. https://doi.org/10.1115/1.4004953.
  » https://doi.org/10.1115/1.4004953.
• Błachut, J., Ifayefunmi, O., and Corfa, M. (2011). Collapse and buckling of conical shells. Proceedings of the International Offshore and Polar Engineering Conference, (June 19-24):887-893. Maui, Hawaii, USA. (ISBN 978-1-880653-96-8).
• Bornscheuer, F.W., and Hafner, L. (1983). The influence of an imperfect circumferential weld on the buckling strength of axially loaded circular cylindrical shells. Proceedings of the Third International Colloquium on Stability of Metal Structures:407-414. Paris, France.
• Castro, S.G.P., Mittelstedt, C., Monteiro, F.A.C., Arbelo, M.A., Ziegmann, G., and Degenhardt, R. (2014). Linear buckling predictions of unstiffened laminated composite cylinders and cones under various loading and boundary conditions using semi-analytical models. Composite Structures 118:303-315. https://doi.org/10.1016/j.compstruct.2014.07.037.
  » https://doi.org/10.1016/j.compstruct.2014.07.037.
• Cui, M.J., and Shao, Y.B. (2015). Residual static strength of cracked concrete-filled circular steel tubular (CFCST) T-joint. Steel and Composite Structures 18(4):1045-1062. https://doi.org/10.12989/scs.2015.18.4.1045.
  » https://doi.org/10.12989/scs.2015.18.4.1045.
• Dinkler, D., and Knoke, O. (2003). Elasto-plastic limit loads of cylinder-cone configurations. Journal of Theoretical and Applied Mechanics 41(3):443-457.
• Estekanchi, H.E., and Vafai, A. (1999). On the buckling of cylindrical shells with through cracks under axial load. Thin-Walled Structures 35(4):255-274. https://doi.org/10.1016/S0263-8231(99)00028-2.
  » https://doi.org/10.1016/S0263-8231(99)00028-2.
• Hafeez, G., El Ansary, A.M., and El Damatty, A.A. (2010). Stability of combined imperfect conical tanks under hydrostatic loading. Journal of Constructional Steel Research 66:1387-1397. https://doi.org/10.1016/j.jcsr.2010.05.007.
  » https://doi.org/10.1016/j.jcsr.2010.05.007.
• Ifayefunmi, O. (2014). A survey of buckling of conical shells subjected to axial compression and external pressure. Journal of Engineering Science and Technology Review 7(2):182-189. https://doi.org/10.25103/jestr.072.27.
  » https://doi.org/10.25103/jestr.072.27.
• Ifayefunmi, O. (2017). Plastic buckling of conical shell with non-continuous edge support. International Journal of Mechanical & Mechatronics Engineering 17:143-152.
• Ifayefunmi, O. (2020). Buckling experiments of cracked axially compressed cones. International Journal of Mechanical and Production Engineering Research and Development 10(3):5665-5674. https://doi.org/10.24247/ijmperdjun2020539.
  » https://doi.org/10.24247/ijmperdjun2020539.
• Ifayefunmi, O., and Błachut, J. (2018). Imperfection sensitivity: a review of buckling behavior of cones, cylinders, and domes. Journal of Pressure Vessel Technology, Transactions of the ASME 140(5):050801-1-050801-8. https://doi.org/10.1115/1.4039695.
  » https://doi.org/10.1115/1.4039695.
• Ifayefunmi, O., Kadmin, A. F., Chang, K. L., and Aziz, A. (2018). Influence of boundary condition on the buckling of axially compressed cones and cylinders. International Journal of Mechanical Engineering and Technology, 9(4):1106 -1116
• Ifayefunmi, O., and Ibrahim, D. D. (2018). The effect of material discontinuity on the flanges of axially compressed steel cones. International Journal of Mechanical Engineering and Technology 9(6):32-41.
• Ifayefunmi, O., and Mahidan, F.M. (2020). Buckling of cracked cones subjected to axial compression, Latin American Journal of Solids and Structures 17(9):1-13.
• Ifayefunmi, O., and Mahidan, F.M. (2021). Collapse of conical shells having single dimple imperfection under axial compression. Journal of Pressure Vessel and Technology 143(1):011301-8. https://doi.org/10.1115/1.4047681.
  » https://doi.org/10.1115/1.4047681.
• Jahromi, B.H., and Vaziri, A. (2012). Instability of cylindrical shells with single and multiple cracks under axial compression. Thin-Walled Structures 54:35-43. https://doi.org/10.1016/j.tws.2012.01.014.
  » https://doi.org/10.1016/j.tws.2012.01.014.
• Khakimova, R., Warren, C. J., Zimmermann, R., Castro, S. G. P., Arbelo, M. A., and Degenhardt, R. (2014). The single perturbation load approach applied to imperfection sensitive conical composite structures. Thin-Walled Structures 84:369-377. https://doi.org/10.1016/j.tws.2014.07.005.
  » https://doi.org/10.1016/j.tws.2014.07.005.
• Mahidan, F. M., and Ifayefunmi, O. (2020a). Buckling of axially compressed cones with imperfect axial length. Latin American Journal of Solids and Structures 17(7):1-20.
• Mahidan, F.M., and Ifayefunmi, O. (2020b). The imperfection sensitivity of axially compressed steel conical shells - lower bound curve. Thin-Walled Structures (in press). https://doi.org/10.1016/j.tws.2020.107323.
  » https://doi.org/10.1016/j.tws.2020.107323.
• Özyurt, E., Yilmaz, H., and Tomek, P. (2017). Prediction of the Influence of Geometrical Imperfection to Load Carrying Capacity of Conical Shells under Axial Loading. Sigma Journal of Engineering and Natural Sciences 52(1):1-20.
• Rotter, J.M. (1996). Elastic plastic buckling and collapse in internally pressurised axially compressed silo cylinders with measured axisymmetric imperfections: interactions between imperfections, residual stresses, and collapse. Proceedings of the International Workshop on Imperfections in Metal Silos: Measurement, Characterisation, and Strength Analysis: 22. Lyon, France.
• Smith, M. (2009). ABAQUS/Standard User’s Manual (Version 6.9), Hibbitt, Karlsson & Sorensen, Inc. (Pawtucket, RI).

Edited by

Editor:

Rogério José Marczak

Publication Dates

• Publication in this collection
  03 May 2021
• Date of issue
  2021

History

• Received
  26 Dec 2020
• Reviewed
  17 Mar 2021
• Accepted
  24 Mar 2021
• Published
  29 Mar 2021