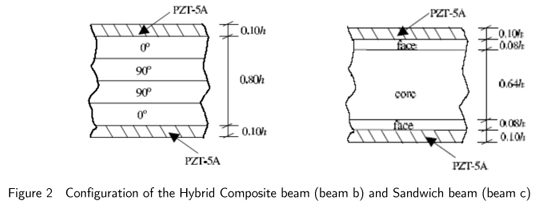
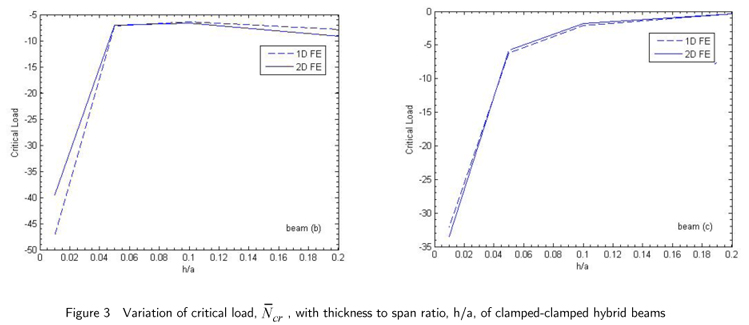
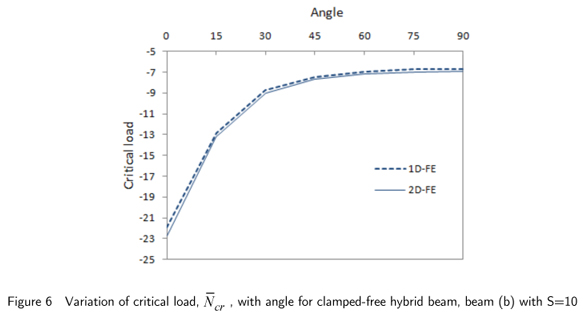
A one-dimensional finite element model for buckling analysis of hybrid piezoelectric beams under electromechanical load is presented in this work. The coupled zigzag theory is used for making the model. The inplane displacement is approximated as a combination of a global third order variation across the thickness with an additional layer wise linear variation. The longitudinal electric field is also taken into account. The deflection field is approximated to account for the transverse normal strain induced by electric fields. Two nodded elements with four mechanical and a variable number of electric degrees of freedom at each node are considered. To meet the convergence requirements for weak integral formulation, cubic Hermite interpolation function is used for deflection and electric potential at the sub-layers and linear interpolation function is used for axial displacement and shear rotation. The expressions for the variationally consistent stiffness matrix and load vector are derived and evaluated in closed form using exact integration. The present 1D-FE formulation of zigzag theory is validated by comparing the results with the analytical solution for simply-supported beam and 2D-FE results obtained using ABAQUS. The finite element model is free of shear locking. The critical buckling parameters are obtained for clamped-free and clamped-clamped hybrid beams. The obtained results are compared with the 2D-FE results to establish the accuracy of the zigzag theory for above boundary conditions. The effect of lamination angle on critical buckling load is also studied.
Piezoelectric beam; FEM; Buckling; Zigzag theory; ABAQUS