Experimental and numerical investigation on the dumbbell-shaped specimen of concrete-like materials under tension

Abstract

Mortar is an important component of concrete. It is of great significance to obtain its tensile properties accurately. The structure heterogeneity of mortar specimens is high. Specimens are prone to fracture nearby interfaces between specimens and loading plates because of the inhomogenous stress distribution during the testing, which leads that effective tensile data can not be easily obtained. Therefore, through the improvement of specimen’s geometrical structure, the dumbbell specimen is designed for quasi-static direct tensile tests. Compared with the splitting test results, the quasi-static direct tensile testing of dumbbell specimens can be availably conducted to obtain the tensile strength. It also provides an effective approach to obtain the tensile parameters of mortar specimens. Moreover, numerical simulations on dumbbell specimens of mortar with different shapes are also conducted to explore the optimal geometrical structure in dynamic direct tensile tests.

Keywords
concrete-like materials; geometric structure; dumbbell specimen; tensile experiments

1 INTRODUCTION

Concrete-like materials (such as the concrete, rocks, and mortar) are widely used in civil construction and military structures, like hydroelectric dams, road tunnels, building constructions and other infrastructures. The strength of concrete-like materials is an important mechanical property, which is the basis to design concrete-like material structures. However, the high heterogeneity of concrete-like materials causes the low success rate of tensile testings with the normal specimens. Malcolm (1983) recommended dumbbell specimens in uniaxial tensile tests on ice and frozen soil. De Baere et al.(2011) employed carbon PPS specimens with dumbbell shape to investigate whether the dumbbell shape is preferable to rectangular in uniaxial fatigue tests on composite materials and found that dumbbell specimens have more advantages in tests. Guiu and Dominguez (1980) introduced dumbbell specimens to measure the internal friction. Jeffrey et al.(2017) used specimens with dumbbell shape to study the dynamic strength of boron carbide. Yan (2006) conducted direct tensile experiments of concrete dumbbell specimens on MTS810 under the strain-rate with 10-5-10-0.3 s-1. Concrete specimens could be fixed to the bonding surfaces through winding several layers of steel wires and using high strength adhesive in dynamic direct tensile tests by Zhang et al.(2016) . The tensile strength could also be measured through indirect methods, such as splitting experiments. Yang et al.(2014) investigated the dynamic tensile performance of mortar by splitting tests, and results showed rate sensitivity.

Mortar is an important component of concrete and it is necessary to accurately obtain its tensile properties. However, available results from quasi-static and dynamic testing of mortar specimens are very limited because mortar specimens have greater structure heterogeneity than other concrete-like materials. Additionally, there still exist some technical problems in quasi-static direct tensile tests, such as eccentricity loading and specimen clamping. When the both axes of cylinder specimens and loading device are not overlapped under tension, the eccentric loading will likely happen in the testing process and lead to the wrong measurement.

At present, there are two main ways to connect specimens with the loading plates in the testing, namely the clamping connection and adhesive bonding. The stress concentration on the interfaces of specimens is unavoidable in direct tensile tests with the clamping connection or adhesive bonding. If the stress becomes too concentrated in the interfaces of specimens, the fracture will occur at the interfaces of specimens and the testing results become invalid. The stress distribution of several common connections and specimen shapes is decribed by Yan (2006) , as illustrated in Figure 1 .

Figure 1
The internal stress distribution in normal and dumbbell specimens with different connections under direct tension

Therefore, the quasi-static tensile experiments of cylindrical mortar specimens are conducted and specimens of dumbbell shape is also considered to reduce the stress concentration on specimen interfaces and improve the accuracy of experimental results in this study. Through that, a more available and effective method is provided for the future research. Based on parameters determined by Zhang et al. (2016) , dynamic direct tensile test models of dumbbell specimens are also established and the parametric analysis about specimen shapes is conducted in this paper.

2 QUASI-STATIC TENSILE TESTS

2.1 Specimen materials and preparation

The cement (P.O 42.5R) used in specimens is produced by Zhonglian cement Co. LTD. The sand (fineness modulus 2.7, medium sand) is the natural river sand collected from the shore of Fujiang river in Mianyang city, Sichuan province, China. The water is the tap water of Mianyang water Co. LTD. The mechanical properties of mortar specimens are closely related to the mixing ratio, and the composition of mortar specimens prepared in this paper is shown in Table 1 .

Table 1
The weight combination ratio of mortar.

Mortar strength grade	Cements	Sand	Water
M40	1.00	1.30	0.40

According to the combination ratio of mortar specimens, raw materials are mixed evenly in a blender, and then the mixed mortar are poured in steel moulds to be enough vibrated in a vibration stand. After that, mortar specimens are covered for 24 hours by plastic films before demoulding. Subsequently, mortar specimens are maintained in a curing box where the humidity and temperature are more than 95% and 20±2 °C, respectively, for at least 28 days, referring to the ‘Standard for Test Method of Mechanical Properties on Ordinary Concrete (GB/T 50081-2002)’. Eventually, mortar specimens are polished to ensure the surface parallelism.

2.2 Testing equipment and procedures

The quasi-static tensile experiments of mortar specimens in this study include quasi-static direct tensile and quasi-static splitting tests. The tensile experiments are conducted on WDW-100 double-column microcomputer control electronic testing system, as shown in Figure 2 .

Figure 2
WDW-100 double-column microcomputer control electronic testing system

The diameter and length of quasi-static splitting test specimens is 75 mm and 37.5 mm (length to diameter ratio is 0.5), respectively. The loading is controlled by displacement (0.01 mm/min). Quasi-static splitting tests of mortar specimens are shown in Figure 3 .

Figure 3
The quasi-static splitting test of the mortar specimen

The arc strips are adopted in quasi-static splitting tests to ensure that the loading strips can suit with the cylinder specimen in the circular direction, which can alleviate the stress concentration problem in the splitting tests. The failure pattern of specimens and loading strips in quasi-static splitting tests are shown in Figure 4 .

Figure 4
The specimen failure pattern and loading strips

In quasi-static direct tensile tests, different length to diameter ratios (specimen length and diameter with 150 mm and 75 mm, specimen length and diameter with 75 mm and 75 mm, specimen length and diameter with 37.5 mm and 75 mm) of cylinder specimens and dumbbell specimens are all used for comparative studies.

Firstly, mortar specimens are connected to loading plates through high strength adhesive and its adhesion strength (more than 20 MPa) is much higher than the tensile strength of mortar specimens. The loading is controlled by the displacement (0.02 mm/min), and the experimental results are terminated by the failure of specimen end surface, as shown in Figure 5 .

Figure 5
Experiment results of a quasi-static direct tensile test of mortar specimen when the slenderness ratio is 2

The two sides of cylindrical specimens are both reinforced by steel tubes and adhesives in consideration of the stress concentration in specimens’ ends under direct tension. The quasi-static direct tensile test of cylindrical specimens with diameter of 75 mm and length of 150 mm is conducted (loading rate is 0.02 mm/min), and the fracture failure occurs in the specimen’s end surface, as shown in Figure 6 .

Figure 6
The modified direct tensile testing of a mortar specimen

Besides, the structure of mortar specimens is further designed and the stress concentration of specimen ends will reduce through processing notches in the middle of specimens. However, these improvements also can not solve the problem of fracture failure in specimen end surfaces, as shown in Figure 7 .

Figure 7
The quasi-static direct tensile test of a mortar specimen when the slenderness ratio is 0.5

Mortar specimens have more non-uniformity than concrete specimens in structure. The structure heterogeneity of mortar specimens is mainly caused by the deposition of cement and sand in the vibration process. Since the cement and sand have larger density, the cement and sand randomly disperse and then sink to the bottom. Therefore, the specimen’s bottom has smaller water cement ratio than that of specimen top, and the strength of specimen’s bottom is higher than that of specimen top in mortar specimens. To minimize the degree of non-uniformity, the length of specimens is casted to 37.5 mm and the diameter is still 75 mm. Despite that, the quasi-static direct tensile tests for specimens whose length to diameter ratio is 0.5 fails again, and specimens fracture around the loading plates.

The structure inhomogeneity of mortar specimens is the main reason why the direct tensile testing fails. Therefore, the water jet is employed to remove top part of the mortar specimen, for reducing the specimen inhomogeneity caused by specimen production problems. After processing, there are two kinds of specimens, viz. the length to diameter ratio with 1 (the diameter and length are both 75 mm) and the length to diameter ratio with 0.5 (the diameter and length are 75 mm and 37.5 mm, respectively). Specimens of the length to diameter ratio with 1 and 0.5 are loaded by the loading rate of 0.01 mm/min and 0.005 mm/min, respectively, to make sure that the loading strain-rate is still consistent to each other. Nevertheless, experimetal results through these improvements are still not ideal, and the fracture occurs at the end surface of specimens, as shown in Figure 8 .

Figure 8
The quasi-static direct tensile test of a mortar specimen treated by the water jet cutter

The structure of mortar specimens is further improved and the dumbbell specimen is considered. The mortar specimens have relatively higher brittleness. To avoid the influence of cutter to the brittle specimens and cracks caused by cutting, dumbbell specimens with gentle oblique angle are adopted in this study, as shown in Figure 9 .

Figure 9
The dumbbell-shaped design of mortar specimens

However, the attempts fails again and the specimen fractures in the specimen end surfaces where the stress is concentrated, as shown in Figure 10 .

Figure 10
The quasi-static direct tensile test of a dumbbell-shaped mortar specimen

Based on the above experiments, a steel tube is employed to the dumbbell specimen and the adhesive reinforces the weak parts of mortar specimens with tube and loading plates. Through that, the dumbbell specimen of mortar finally breaks within the effective fracture zone under loading rate with 0.01 mm/min, as shown in Figure 11 .

Figure 11
The quasi-static direct tensile test of a dumbbell-shaped mortar specimen with the tube

2.3 Tensile strength

The strength of mortar specimens in the quasi-static tensile testing can be calculated by the strength definition,

$$P_{static}=\frac{F_{peak}}{\pi r^2}$$ (1)

in which, $P_{static}$ is the strength of mortar specimens in the quasi-static tensile testing, $F_{peak}$ stands for the peak loading of mortar specimens in the quasi-static tensile testing, $\pi$ is the ratio of the circumference of a circle to its diameter (its value is 3.141592654 in this paper),and $r$ is the specimen radius.

The strength of mortar specimens in quasi-static splitting testing can be calculated through the following equation recommended by Tang (1994) ,

$$P_{split-s}=\frac{2F_{p-s}}{\pi DL}{(1-{\beta }^2)}^{3/2}$$ (2)

$$\beta =b/D$$ (3)

where $\beta$ is the relative width of the arc strips, b stands for the width of arc strips, L is the length of arc strips, D is the diameter of mortar specimens, $F_{p-s}$ stands for the peak loading of mortar specimens,and $P_{split-s}$ is the strength of mortar specimens in the quasi-static splitting testing when $\beta$ is greater than 0 and less than 0.2.

2.4 Results and analysis

According to the theoretical formula (1) and (2) , experimental results from quasi-static tensile testing are shown in Table 2 .

Table 2
The quasi-static tensile strength of mortar specimens.

Experimental type	Strength (MPa)	Difference–value (MPa)	The proportion of intermediate strength and value difference	Remarks
Quasi-static Splitting testing	4.28	0.89	17.21%	$\beta =0.17$
	5.17	0	0.00%
	6.77	1.60	30.95%
Quasi-static Direct tension	3.68	0.43	13.23%	Dumbbell Specimen
	3.25	0	0.00%
	2.97	0.28	8.62%

GB/T 50081-2002 (Standard for Test Method of Mechanical Properties on Ordinary Concrete) mentions the validity of experimental results: ‘When there are three measured data and a ratio between the difference-value and intermediate strength is less than 15% and another ratio of that is more than 15%, the intermediate strength can be regarded as the strength of mortar specimens; moreover, if the ratio between the difference-value and intermediate strength are both larger than 15%, the experimental results are invalid; in addition, the average strength can be taken as the strength of mortar specimens as long as there are three measured data and the two ratios between the difference-values and intermediate strength are both less than 15%’. Rocco et al(2001) also thought that the splitting strength can not be considered as the material strength and the dispersion caused by the specimen geometry and boundary condition (especially to bearing strips) will be noticeable for ordinary strength concrete even if the difference will be smaller for more brittle material.

Therefore, the experimental results of quasi-static splitting testing can not represent the tensile strength of mortar specimens. The average tensile strength of dumbbell specimens in the quasi-static direct tensile testing can be considered to be the quasi-static tensile strength of mortar because the ratios between the difference-values and intermediate strength are both less than 15%. The tensile strength of dumbbell specimens is 3.3 MPa.

In this paper, it can be found that the splitting strength of mortar is greater than the direct tensile strength of mortar. Mortar specimens in the state of splitting where stretching and compression exist will have more complicated situations than specimens in the state of direct tension, because the strength measured under splitting is affected by tensile and compressive stress. In addition to the influence of stress state, mortar specimens under splitting should be observed to estimate whether specimens are cracked from the center and judge whether experiments are valid. In the splitting experiments, the damage process of specimens is short and the crack propagation is fast, which brings some difficulties to the determination of final testing results. Therefore, it is necessary to use high-speed photography to assist crack observation in splitting tests, and eventually determine whether the tests are valid. Moreover, the boundary conditions also has the influence to the results. Jin et al(2017) also considered that the splitting specimen is not under the strict plane stress state and the size effect also exist in the quasi-static splitting testing, which will cause the measuring error.

Compared results of dumbbell specimens also seemingly indicate that the tensile strength of dumbbell specimens is related to the fracturing position in dumbbell specimens, as shown in Figure 12 .

Figure 12
Results from quasi-static direct tensile tests of dumbbell-shaped mortar specimens

From Figure 12 , the strength from the dumbbell specimen that fractures around the bottom of effective area is lower than that in the center section of effective area. Moreover, the fracturing position of specimens is usually the weakest area of specimens in quasi-static direct tensile tests. The weak area is closely related to the whole production process of specimens, such as the agitation and oscillation situations and curing in the hydration of mortar specimen, the processing feed speed of shaping to dumbbell and so on. These factors should be avoided as far as possible. Therefore, it is advisable to use moulds to cast dumbbell specimens of mortar in the same batch in the future experiments.

3 DYNAMIC NUMERICAL SIMULATION ON DUMBBELL SPECIMENS

Specimens of concrete-like materials with high degree of heterogeneity have the problem of local stress concentration. The success rate of dynamic direct tensile tests for these materials is also not high. The heterogeneity of mortar is relatively higher than that of concrete, which causes the high failure rate of mortar specimens in dynamic direct tensile tests. The structure of dumbbell shape can reduce the degree of stress concentration in specimens and make the loading stress mainly act on the effective fracture zone of specimens. However, whether the dumbbell specimens can be used in dynamic direct tensile tests need to be further analyzed.

The split Hopkinson tension bar (SHTB) has been usually employed to study the dynamic performance of concrete-like materials in the laboratory, mainly including the incident bar, transmitter bar, projectile and strain gauges, as shown in Figure 13 .

Figure 13
The illustration of SHTB device

The compressive strength is also one important parameter to determine the internal friction angle in numerical simulations. Therefore, the quasi-static compressive testing is conducted as shown in Figure 14 and Figure 15 .

Figure 14
The position of a specimen and loading plates

Figure 15
The failure pattern of a specimen

The diameter and length of mortar specimens for quasi-static compressive testing is 75 mm and 37.5 mm, respectively, to match the size of specimens in dynamic numerical simulations.

The specimen is placed in the middle of the loading plates. After that, the specimen is loaded with loading rate of 2.4 KN/s to be tested. The position and failure pattern of the specimen are shown in Figure 14 and Figure 15 , respectively. The average peak loading of quasi-static compression is 260.6 KN, and the quasi-static compressive strength of mortar is 58.99 MPa.

3.1 Numerical model

In this paper, the Drucker-Prager constitutive model for concrete-like materials in ABAQUS is employed to simulate the dynamic performances of mortar specimens under dynamic direct tension. The hydrostatic pressure, internal friction flow stress, strain strengthening/softening and strain-rate sensitivity are all considered in the Drucker-Prager constitutive model. The strain-rate effect can be defined as the following equations recommended by Hao et al. (2012) ,

$$DIF=\mathrm{1.0,}{\dot{\epsilon }}_s<{10}^{-4}{s}^{-1}$$ (4)

$$DIF=0.26\log {\dot{\epsilon }}_s+{\mathrm{2.06,10}}^{-4}{s}^{-1}<{\dot{\epsilon }}_s<1s^{-1}$$ (5)

$$DIF=2\log {\dot{\epsilon }}_s+\mathrm{2.06,}{\dot{\epsilon }}_s>1s^{-1}$$ (6)

The internal friction angle of dumbbell specimens in numerical simulations can be obtained by the following equation,

$$\theta ={\sin }^{-1}(\frac{{\sigma }_{cs}-{\sigma }_{ts}}{{\sigma }_{cs}+{\sigma }_{ts}})$$ (7)

in which, ${\sigma }_{cs}$ is the quasi-static compressive strength of mortar, ${\sigma }_{ts}$ stands for the quasi-static tensile strength of mortar.

Through Eq.(7) , the internal friction angle is taken as 57.158 ̊, and dilation angle and flow ratio can be considered as 57.158 ̊ and 1, respectively. The geometrical dimensions and material parameters in numerical simulations are shown in Table 3 .

Table 3
Parameters of dumbbell-shaped specimens in dynamic direct tensile simulations.

	Dimensions		Material properties
	Length (mm)	Diameter (mm)	Material	E (GPa)	ρ (kg/m3)	ν
Incident bar	2400	75	Steel	210	7800	0.3
Specimen	37.5	75	Concrete	26.61	2400	0.2
Transmitted bar	3500	75	Steel	210	7800	0.3

Note: the length of the incident bar in this table is the distance from the strain gauge to the incident surface between incident bar and specimen.

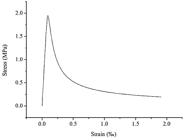
In the numerical model, elements are CAX4R (4-node bilinear axisymmetric quadrilateral, reduced intergration, hourglass control), and the interval of elements is 1 mm. The total computation time of the model is 1300 μs. The contact between specimens and incident bar and transmission bar can be defined as ‘tie’. The quasi-static tensile stress-strain of mortar in the numerical model is consistent with the experiments conducred by Zhang et al.(2016) , as shown in Figure 16 .

Figure 16
The quasi-static tensile stress-train curve of mortar specimens

The amplitude of stress wave in the incident bar is based on the signal collected by the strain gauge on incident bar in laboratory experiments, as shown in Figure 17 .

Figure 17
The amplitude of incident wave in laboratory tests and its smoothed curve

The axisymmetric model of dumbbell specimens with different shapes and geometries are shown in Figure 18 and Figure 19 , respectively.

Figure 18
The triangle dumbbell specimens

Figure 19
The dumbbell specimens with circular shape

In Figure 18 and Figure 19 , specimen nodes are in good contact with the nodes of incident bar and transmitter bar to ensure the effective transmission of stress wave in numerical models. The dumbbell specimens will be compared with solid specimens to investigate whether the dumbbell specimen is preferred to the solid specimen in dynamic direct tensile testing.

3.2 Results and discussion

The dynamic tensile strength and strain-rate of specimens can be obtained through following equations,

$${\sigma }_d(t)=\frac{A_H{E}_H}{2A_S}\left[{\epsilon }_i(t)+{\epsilon }_r(t)+{\epsilon }_t(t)\right]=\frac{A_H}{2A_S}\left[{\sigma }_i(t)+{\sigma }_r(t)+{\sigma }_t(t)\right]$$ (8)

$${\dot{\epsilon }}_d(t)=\frac{C_H}{l_a}\left[{\epsilon }_i(t)-{\epsilon }_r(t)-{\epsilon }_r(t)\right]=\frac{C_H}{E_H{l}_a}\left[{\sigma }_i(t)-{\sigma }_r(t)-{\sigma }_t(t)\right]$$ (9)

where, ${\sigma }_d(t)$ is the dynamic tensile stress of specimens at the time of t, $A_H$ stands for the sectional area of incident and transmit bar, $E_H$ is the Young’s modulus of Hopkinson bar, $A_S$ is the sectional area of the effective fracture zone, ${\epsilon }_i(t)$ , ${\epsilon }_r(t)$ and ${\epsilon }_t(t)$ represent the incident, reflected and transmitted strain obtained from the Hopkinson bars at time of t, respectively, ${\sigma }_i(t)$ , ${\sigma }_r(t)$ and ${\sigma }_t(t)$ are the incident, reflected and transmitted stress at time of t, respectively, ${\dot{\epsilon }}_d(t)$ is the strain-rate of specimens at the time of t, $C_H$ is the the propagation velocity of stress wave in the Hopkinson bar, and $l_a$ is the length of effective fracture zone.

Under the loading of high strain-rate, the waveform dispersion may occur in large diameter bars and it will result in the deviation of experimental results. Therefore, the dynamic stress equilibrium should be estimated in numerical simulations.

The degree of stress equilibrium of specimens can be measured in dynamic testing through the stress equilibrium factor recommended, as shown in following equation,

$$R(t)=2\left|\frac{p_1(t)-p_2(t)}{p_1(t)+p_2(t)}\right|$$ (10)

in which, $R(t)$ is the stress equilibrium factor at the time of t, and $p_1(t)$ and $p_2(t)$ stand for the average axial loading of the contacting surfaces between the specimen and incident or transmitted bar, respectively.

If the stress in specimens is more uniform, the value of stress equilibrium factor will be smaller. The axial stress state of specimens can be considered to be uniform in experiments when the value of stress equilibrium factor is around or below 0.05.

According to Eq.(10) , the comparative analysis of solid and dumbbell specimens is conducted and results under different strain-rates are all shown in Table 4 .

Table 4
The analyzed results among conventional specimens and two kinds of dumbbell-shaped specimens.

	Loading (MPa)	DIF	Strain-rate (s-1)	R
Solid	20	1.36	58.61	0.056
	22	1.52	64.26	0.076
	23	1.59	82.03	0.067
	25	1.74	86.73	0.061
	30	2.12	108.71	0.001
	35	2.47	118.51	0.096
	40	2.86	133.34	0.035
	45	3.19	163.29	0.068
	55	3.82	166.88	0.097
	75	5.33	264.11	0.085
Circle-4 mm	15	1.33	69.20	0.037
	17	1.48	77.42	0.010
	20	1.76	83.59	0.002
	22	1.94	92.09	0.069
	24	2.11	100.29	0.017
	25	2.20	102.19	0.022
	35	3.11	161.25	0.033
	55	4.92	232.36	0.061
	75	6.74	327.22	0.019
Circle-8 mm	10	1.10	53.08	0.051
	13	1.42	85.35	0.041
	15	1.66	92.67	0.037
	16	1.78	99.22	0.046
	18	2.01	105.25	0.052
	19	2.13	111.21	0.050
	20	2.24	117.14	0.068
	25	2.80	138.89	0.027
	30	3.35	186.57	0.073
	32	3.54	193.55	0.034
	35	3.95	219.14	0.016
	40	4.53	243.59	0.060
	75	8.54	458.49	0.030
Triangle-4 mm	10	1.23	55.29	0.022
	15	1.24	56.47	0.054
	17	1.40	62.85	0.060
	20	1.63	71.93	0.048
	25	2.17	106.41	0.054
	27	2.35	115.38	0.056
	30	2.67	119.52	0.072
	32	2.67	119.52	0.122
	35	3.08	131.67	0.084
	55	5.02	250.35	0.143
	75	6.74	318.54	0.070
Triangle-8 mm	10	1.07	54.87	0.038
	13	1.40	67.61	0.030
	14	1.48	71.85	0.026
	15	1.62	101.27	0.040
	16	1.75	101.49	0.046
	17	1.87	104.78	0.057
	18	1.95	113.32	0.053
	20	2.27	121.97	0.089
	23	2.60	131.38	0.060
	24	2.65	134.90	0.086
	25	2.80	172.35	0.067
	35	3.91	194.27	0.084
	55	6.38	340.03	0.091
	75	8.54	443.70	0.050

From Table 4 , the dynamic tensile strength of mortar increases with the loading, and the dynamic strength enhancement of dumbbell specimens is more obvious than that of solid specimens, because the effective fracture zone of dumbbell specimens is shorter than the length of solid specimens and the strain-rate of dumbbell specimens is larger than that of solid specimens under the same loading condition. Moreover, the stress equilibrium factor of dumbbell specimens with triangular shape is lower than that of dumbbell specimens with circular shape under dynamic direct tension.

In this paper, the stress distribution of dumbbell specimens with circular and triangular shape is also compared, as shown in Figure 20 .

Figure 20
The stress (with unit of Pa) distribution of dumbbell-shaped specimens under tensile loading with 20 MPa when the dynamic axial stress reaches the peak

In Figure 20 , the stress of dumbbell specimens with triangular shape has more uniform distribution, compared with that of dumbbell specimens with circular shape.

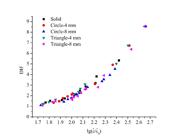
The relationship of dynamic tensile DIFs and strain-rate calculated through Eqs.(8) and (9) are shown in Figure 21 .

Figure 21
The relationship between the dynamic tensile DIFs and strain-rate of dumbbell specimens of mortar

In Figure 21 , results show that the DIFs have an exponential growth and curves of DIFs versus strain-rate of solid and dumbbell specimens with different shape are basically in coincidence with each other, which indicates the effectiveness of dumbbell specimens under dynamic direct tension.

4 CONCLUSION

In this paper, the quasi-static direct tensile testing and numerical simulations of dynamic direct tensile experiment of mortar are both conducted to investigate the feasibility of dumbbell specimens. The main results are as following,

1. 1

   The dumbbell specimen is imposed in quasi-static direct tensile tests, and it can overcome the fracture problem caused by the inhomogeneous stress distribution and make the fracturing occur within the effective fracture zone. Therefore, dumbbell-shaped specimens made by moulds can be used to measure static performances of concrete-like materials in the future experiments.

2. 2

   Through the comparative results of quasi-static splitting and direct tensile tests, it can be found that the splitting experiment has intrinsic measurement errors caused by the measurement method, which indicates that the improved dumbbell specimen of mortar is more advantageous in direct tension.

3. 3

   The stress distribution of dumbbell specimens with triangular shape is more uniform than that of dumbbell specimens with circular shape, which means dumbbell specimens with triangular shape is more suitable for the strength measurement of concrete-like materials in dynamic direct tensile tests.

4. 4

   The curves of DIFs and strain-rate from mortar dumbbell and solid specimens are consistent with each other, and it confirms the measuring effectiveness of dumbbell specimens in dynamic direct tensile tests.

• http://dx.doi.org/10.1590/1679-78254632

References

• Rocco, C., Guinea, C.V., Planas, J., Elices., M., (2001). Review of the splitting-test standards from a fracture mechanics point of view, Cement and Concrete Research 31(1):73-82.
• De Baere, I., Van Paepegem, W., Hochard, C., (2011). On the tension-tension fatigue behavior of a carbon reinforced thermoplastic part II: Evaluation of a dumbbell-shaped specimen, Polymer Testing 30(6):663-672.
• GB/T-50081 (Ministry of Construction of PRC) (2002). Standard for Test Method of Mechanical Properties on Ordinary Concrete. (in Chinese)
• Guiu, F., Dominguez, U., (1980). Measurement of internal friction using a resonant dumb-bell-shaped specimen, Physica Status Solidi A-applied Research 57(1):155-162.
• Hao, Y.F., Hao, H., Zhang, X.H., (2012). Numerical analysis of concrete material properties at high strain rate under direct tension, International Journal of Impact Engineering 39(1):51-62.
• Jeffrey J.S., Christopher S.M., Daniel, T.C., William, R.G., (2017). Casem,et al. Static and dynamic compression strength of hotpressed boron carbide using a dumbbell-shaped specimen, Ceramics 52(17):1-12.
• Jin, X.C., Hou, C., Fan, X.L., Lu, C.S., Yang, H.W., Shu, X.F., Wang, Z.H.,(2017). Quasi-static and dynamic experimental studies on the tensile strength and failure pattern of concrete and mortar discs, Scientific Reports, 7(1):1-15.
• Malcolm, M., (1983). Strain measurements on dumbbell specimens, Cold Regions Science and Technology 8(1):75-77.
• Tang, T., (1994). Effect of load-distributed width on split tension of unnotched and notched cylindrical specimens, Journal of Testing and Evaluation 22(5):401-409.
• Yan, D.M., (2006). Experimental and theoretical study on the dynamic properties of concrete, PHD Thesis (in Chinese), Dalian University of Technology, China.
• Yang, F., Ma, H.W., Lin, J., Zhao, L.M., Wang, Z.H., (2014). Dynamic compressive and splitting tensile tests on mortar using split Hopkinson pressure bar technique, Latin American Journal of Solids and Structures 12(4):730-746.
• Zhang, S., Lu, Y.B., Chen, X., Teng, X., Yu, S.S., (2016). Further investigation on the real rate effect of dynamic tensile strength for concrete-like materials, Latin American Journal of Solids and Structures 13(1):201-223.

Publication Dates

• Publication in this collection
  02 July 2018
• Date of issue
  2018

History

• Received
  30 Oct 2017
• Reviewed
  06 May 2018
• Accepted
  14 May 2018