Abstract
Precast bridge columns have shown increasing demand over the past few years due to the advantages of such columns when compared against conventional bridge columns, particularly due to the fact that precast bridge columns can be constructed off site and erected in a short period of time. The present study analytically investigates the behaviour of self-centring precast segmental bridge columns under nonlinear-static and pseudo-dynamic loading at different prestressing strand levels. Self-centring segmental columns are composed of prefabricated reinforced concrete segments which are connected by central post-tensioning (PT) strands. The present study develops a three dimensional (3D) nonlinear finite element model for hybrid post-tensioned precast segmental bridge columns. The model is subjected to constant axial loading and lateral reverse cyclic loading. The lateral force displacement results of the analysed columns show good agreement with the experimental response of the columns. Bonded post-tensioned segmental columns at 25%, 40% and 70% prestressing strand stress levels are analysed and compared with an emulative monolithic conventional column. The columns with a higher initial prestressing strand levels show greater initial stiffness and strength but show higher stiffness reduction at large drifts. In the time-history analysis, the column samples are subjected to different earthquake records to investigate the effect post-tensioning force levels on their lateral seismic response in low and higher seismicity zones. The results indicate that, for low seismicity zones, post-tensioned segmental columns with a higher initial stress level deflect lower lateral peak displacement. However, in higher seismicity zones, applying a high initial stress level should be avoided for precast segmental self-centring columns with low energy dissipation capacity.
Precast segmental columns; post-tensioning forces; energy dissipation capacity; lateral peak displacement; finite element method
A numerical study on seismic response of self-centring precast segmental columns at different post-tensioning forces
Ehsan NikbakhtI,** Author email: enikbakht@siswa.ukm.edu.my.; Khalim RashidI; Farzad HejaziII; Siti A. OsmanI
IDepartment of Civil and Structural engineering, Universiti Kebangsaan Malaysia, 43600 Bangi, Malaysia
IIDepartment of Civil and Structural engineering, Universiti Putra Malaysia, 43000 Serdang, Malaysia
ABSTRACT
Precast bridge columns have shown increasing demand over the past few years due to the advantages of such columns when compared against conventional bridge columns, particularly due to the fact that precast bridge columns can be constructed off site and erected in a short period of time. The present study analytically investigates the behaviour of self-centring precast segmental bridge columns under nonlinear-static and pseudo-dynamic loading at different prestressing strand levels. Self-centring segmental columns are composed of prefabricated reinforced concrete segments which are connected by central post-tensioning (PT) strands. The present study develops a three dimensional (3D) nonlinear finite element model for hybrid post-tensioned precast segmental bridge columns. The model is subjected to constant axial loading and lateral reverse cyclic loading. The lateral force displacement results of the analysed columns show good agreement with the experimental response of the columns. Bonded post-tensioned segmental columns at 25%, 40% and 70% prestressing strand stress levels are analysed and compared with an emulative monolithic conventional column. The columns with a higher initial prestressing strand levels show greater initial stiffness and strength but show higher stiffness reduction at large drifts. In the time-history analysis, the column samples are subjected to different earthquake records to investigate the effect post-tensioning force levels on their lateral seismic response in low and higher seismicity zones. The results indicate that, for low seismicity zones, post-tensioned segmental columns with a higher initial stress level deflect lower lateral peak displacement. However, in higher seismicity zones, applying a high initial stress level should be avoided for precast segmental self-centring columns with low energy dissipation capacity.
Keywords: Precast segmental columns; post-tensioning forces, energy dissipation capacity, lateral peak displacement; finite element method
1 INTRODUCTION
In recent years, precast segmental bridges have attracted the interest of researchers. The reason is that precast segmental bridge construction is capable of accelerating the construction period, thereby avoiding significant periods of traffic disruption during bridge construction; and making higher quality construction possible. Another advantage of this system is that it is more economic than emulative conventional monolithic systems, because after a severe earthquake it will be reparable due to the minor induced damage and cracking.
Precast hybrid post-tensioned constructions have been investigated by many researchers in recent years. Stanton et al. (1998) apply the concept of a hybrid system for a reinforced frame and demonstrate that the combination of energy dissipating mild steel reinforcement and recentring prestressed strands can meet the required objectives of a design, while having less damage and residual displacement. A number of researchers investigate unbonded and bonded post-tensioned segmental concrete bridge piers experimentally in recent studies (Hewes and Priestley 2002, Palermo and Pampanin 2007, Ou-Chen et al. 2010b, Elgawady et al. 2012).
However, precast segmental bridge columns have a low energy dissipation capacity compared with conventional monolithic columns. This deficiency can be removed by controlling for the flag shaped behaviour by selecting an appropriate combination of post tensioning (PT) strands and mild steel reinforcement. For instance, Palermo et al. (2005) and Ou-Chen et al. (2010a) propose a combination ratio of energy dissipating mild steel and PT strands as one of the main design factors in hybrid post-tensioned bridges to achieve high energy dissipation capacity against earthquake loading with less damage and residual displacement against seismicity. Other researchers also propose solutions for increasing energy dissipation of the segmental columns. Shim et al. (2008) experimentally investigate whether precast segmental columns with internal steel tubes around the PT strands for improve the hysteretic performance of such columns in regards to energy dissipation. Kim et al. (2010) apply continuous shear resistant bars across the segments and footings in order to increase the energy dissipation and ductility of precast segmental columns. Marriot et al. (2010) examine unbonded post-tensioned precast bridge piers with external, fully replaceable dissipaters. Motaref (2011) conducts an experimental and analytical study on precast segmental columns with energy dissipating joints.
Precast hybrid post-tensioned segmental columns have also been investigated analytically by researchers over the past few years. Hewes and Priestley (2002) apply a monolithic beam analogy concept and develop a method for predicting the push over lateral force displacement of precast segmental columns based upon the assumption that the major opening occurs at the joint base of precast columns. Ou-Chen et al. (2007, 2010b) extend the previous method for post-tensioned segmental columns to predict the pushover lateral force-displacement behaviour of precast segmental bridge columns with unlimited segments. Palermo et al. (2005) use two rotational springs: one representing the behaviour of prestressed tendons without the contribution of mild steel reinforcement; and the other representing only the mild steel reinforcement contribution. Kwan and Billington (2003) also propose some criteria concerning the functional and survival limits for post- tensioned precast segmental bridge columns. Chou et al. (2008) develop a hysteretic model for an unbonded precast segmental concrete filled steel tube (CFT). Dawood et al. (2012) develop threedimensional finite element models to predict the monotonic behaviour of precast segmental bridge columns. The precast segmental columns are retrofitted and the lateral loading is repeated to investigate the accuracy of analytical results for predicting induced damages.
Although precast PT segmental bridge columns have shown satisfactory performance in relation to the benefits of reparability after earthquake loading, a lack of knowledge exists regarding the utilisation of such columns in high seismicity zones. Additionally, little extant research exists concerning the performance of precast segmental columns against realistic ground motions. The present study examines precast segmental self-centring columns with central PT strands and adequate transverse confinement which possess inherent low energy dissipation capacity. In such a system, PT force level is one of the most important design factors in seismic zones. The present study analytically evaluates the hysteretic performance of precast self-centring segmental columns at different post-tensioning force levels. Moreover, as the International Code Council (ICC 2006) requires the behaviour of monolithic conventional structures to be emulated for precast concrete structures in seismic zones, the lateral seismic response of precast segmental columns are compared to the lateral seismic response of conventional bridge columns. In addition to nonlinear reverse cyclic loading, pseudo-dynamic analyses are also performed to conduct a detailed study on the influence of post-tensioning force levels on the stiffness, strength, lateral peak seismic demand, stiffness reduction and energy dissipation capacity of bonded post-tensioned precast segmental columns as a result of real ground motion excitation.
2 POST-TENSIONING STRANDS TENSION CRITERIA
Prestressing initial stress has a significant effect on the behaviour of precast hybrid segmental bridge columns. ACI318-02 (2002) does not allow a final stress higher than 80% of tensile strength of the strands, while the Masonry Standards joint Committee (MSJC 2005) limits final stress to 78% of the tendon yield stress. Initial prestressing occurs in the elastic stage. If the strain of the strands exceeds the yielding strain during the rocking of the column's segments, strands lose some initial force (Fig. 1). When the tendon reaches the second strain limit, post tensioning strands will lose their force and stiffness considerably where the sliding of segments occurs. The total strand strain at lateral deformation in precast walls can be expressed in Eq. 1, as indicated by Wight et al. (2007).
where; εps is the total post-tensioning strain during the rotation of the wall, εrock is the rocking elongation strain, εpi is the initial strain of post-tensioning force, ΔT is the lateral displacement of the wall, he is the height of the segment and lp is the length of the post-tensioning strands.
3 NUMERICAL ANALYSIS
In order to investigate the effect of post-tensioning forces on the behaviour of precast segmental bridge columns under real earthquake loading, the results obtained by the nonlinear finite element method are firstly compared and validated with experimental work done by Hewes and Priestley (2002). Then, precast PT samples and emulative conventional monolithic bridge columns are analysed under nonlinear-static and pseudo-dynamic loading. For this purpose, a threedimensional (3D) finite element program ANSYS (2012) is utilised. The details of the geometry; properties of the experimented precast segmental column sample; post-tensioning and loading program; boundary conditions; and failure criteria are described below.
3.1 Sample description
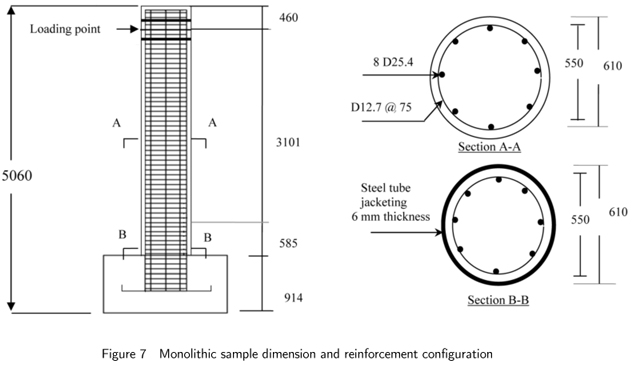
The sample utilised in the present study consists of four segments and a footing foundation connected by unbonded continuous strands. The dimensions and geometry of the sample is shown in Fig. 2. Steel tube jacketing with a thickness of 6 mm encases the first segment, starting from 25 mm above the base of the footing. 27 D12.7 mm strands are placed in a hollow duct at the centre of the column measuring 140mm in diameter. The longitudinal reinforcement is discontinuous at the joint of the segments in order to assist the rocking action of segments when joint opening occurs. Transverse spirals are also spaced at 75 mm along the height of the column.
The material properties for the concrete; transverse and longitudinal reinforcement; steel tube jacketing; and PT strands are shown in Table 1.
3.2 Loading program procedure
Three types of loading are imposed at the three stages outline below: post-tensioning, axial and lateral cyclic. The footing is fixed at the bottom in all stages.
1. Post-tensioning of prestressed strands at the centre of the column. A 2230 kN equivalent of 40% of the tension yielding capacity of 27 prestressing strands, 12.7 mm diameter, are applied during this stage.
2. Applying an axial force of 890 kN at the top of the column, representing the weight of the bridge deck, which is equivalent to 0.08 f'cAg.
3. Lateral cyclic loading at the loading point of 303mm above the column at the loading head. The cyclic loading history is shown in Fig. 3. The loading is imposed as 0.6%, 0.9%, 1.2%, 1.6%, 2.2%, 3% and 4% drift displacement. Three cycles of loading are repeated for each drift level. Two criteria are applied regarding the functionality failure of the columns: the yielding of PT strands; and the occurrence of a 1% residual drift during the loading.
3.3 Types of elements
During the simulation of the precast segmental bridge columns, elements for the modelling of materials, such as concrete, mild steel reinforcement, transverse spirals, steel tube jacketing, PT strands and segments joints, must be selected accordingly to derive precise results concerning stiffness, yielding displacement, strength energy dissipation and residual displacement under reverse cyclic and seismic loading.
Fig. 4(a) shows the sample's segments. The elements applied for longitudinal and transverse mild steel reinforcement, PT strands and steel tube jacketing are shown in Fig. 4(b), while the meshing configuration of the sample is shown in Fig. 4(c). The details of applied elements; and their relevant properties and coefficients are as follows.
A Solid65 element is used for the modelling of the concrete and is defined with 8 nodes and three degrees of freedom at each node. The element has the capability to show cracking, crushing and nonlinear plastic deformation when the concrete is under tension. The compressive stress- strain of concrete is obtained using Eqs. (3-4)(Desayi and Krishnan 1964).
3.1.4 Stress-controlled tensile test: Case 4
Similarly to the previous cases, in this case, the tensile test is controlled by the applied axial stresses with maximum values of 20 MPa and 26 MPa that are linearly applied during a short time step of 1/24 day and then maintained constant. Figure 4 shows the curves of strain versus time and damage versus time. Note that in both these instances, the applied loads are less than the plastic yield value of 50 MPa. However, due to hydrolytic damage, plasticity is finally achieved, thereafter driving the material point to collapse.
where ε0 is the strain at the ultimate compressive strength of concrete; and Ec is the elastic modulus of the concrete (MPa) up to 30% of the compressive strength of the concrete.
The Link8 element is used for longitudinal and transverse spirals mild steel reinforcement. It has the capability of plasticity, swelling, and large deflection.
Shell181 is used for the steel tube jacketing. This element is appropriate for analysing thin and moderate shells. It is defined with four nodes with six degrees of freedom at each node.
During the occurrence of segment uplift, the stiffness of the contact elements at the joints must be zero and no penetration should be considered while closing the segments at the unloading stages. For this purpose, both the Contact174 and Target170 possess unilateral flexible surface to surface attributes and the penalty method contact algorithm is selected to model the contact between the segments. According to an ACI recommendation, a coefficient for friction of 0.5 is used for the friction between the surfaces of two adjacent segments. For modelling the contact between the unbounded PT strands and hollow ducts, surface to surface Contact and Target elements have been implemented.
Solid185 element is used for the post-tensioning strands. This element has the capability of large deflection, plasticity and large strain. The Prets179 element is used for distributing the pretension force in the PT strand. The Prets179 element has one degree of freedom in one translational direction and acts between meshed solid elements (in this case Solid185). By creating a section at the middle of the element specified, the Prets179 element spreads pretension force through the coincident nodes. Three defined nodes are utilised for distributing the pretension force in this element: two created coincident nodes; and a third node through which the direction of force is specified.
Bilinear elastic-perfectly plastic stress-strain has been assumed for the longitudinal, transverse and PT strands.
3.4 Concrete failure criteria
In the finite element method, the mostly multi linear isotropic Von Mises formula (Wolanski 2004) is used to show the limit of critical stress for the principle space stresses of the three axes and the concrete begins to yield when the induced stress exceeds the critical stress limit established in Equation 5. The Willam and Warnke (1974) model has been used for surface failure criteria for determining the conical surface failure of concrete (Eq. 6).
where σe is the critical stress; σ1, σ2 and σ3 are the principle stresses; σaand τa are average stress components; fcu is the ultimate compressive strength of concrete; Z is the surface apex; r(θ) is a position vector with θ (angle of similarity); and f(σ) is conical failure surface.
4 VALIDATION AND VERIFICATION
Fig. 5 shows a comparison of the cyclic lateral force-displacements of the unbounded segmental sample predicted by the finite element method utilised in the present study (FEM) and the experiment (EXP). It is clear from the figure that the FE closely follows the experimental results. In Table 2, the maximum and minimum lateral force of the experimental and numerical results is compared for every drift level. This sample was analysed with up to 3% lateral drift (108.9 mm) because concrete spalling has occurred in the second segment at the joint of the first segment area (Fig. 6). The cracking and crushing of this area are shown in figure and is compared with the experimental results, which are consistent. The difference between the FE and experimental results is less than 6.6%, which demonstrates the accuracy of the predicted lateral force-displacement results by the FE model developed in the present study.
5 PRECAST BONDED PT SEGMENTAL AND MONOLITHIC COLUMN SAMPLES
In this part, the bonded precast PT segmental column has been analysed to investigate the effect of interaction of concrete and strands on the energy dissipation, strength and stiffness of the sample described in the previous sections. The emulative monolithic conventional column (Fig. 7) has also been analysed to assess the overall performance of the precast segmental columns under nonlinear- static loading. All conditions for the loading and concrete properties of these samples are the same as the unbonded sample, with two exceptions: there is interaction between the concrete and strands in the bonded samples; and there is no PT strand in the monolithic column. The arrangement and properties of the reinforcement in the monolithic sample is selected so that the nominal shear strength of the bonded and monolithic bridge columns are the same (Table 3).
6 COMPARISON OF UNBONDED AND BONDED PT SEGMENTAL COLUMNS
In the present study, the performance of bonded and unbonded PT segmental samples under cyclic loading is investigated. Compared to the bonded PT segmental column, the unbonded system is advantageous for delaying the yielding of the PT strands because the post-tensioning force is distributed throughout the height of the strands in the unbonded system. Fig. 8 shows the comparison of cyclic lateral force-displacement and cumulative energy dissipation in bonded and unbonded column samples with up to 3% drift (108.9 mm). The thin area enclosed by each cycle in the graph indicates that generally the energy dissipation capacity of the bonded and unbonded post-tensioned columns is low. The results depicted in Fig. 8(a) indicate that the bonded column has a higher strength (252 kN versus 220 kN strength of unbonded column), while no significant difference in the initial stiffness exists between the two samples. Fig. 8(b) also shows that the cumulative energy dissipation of the bonded column is higher, which is primarily due to induced cracks and damage to the concrete around the central strands in the bonded column. Besides, the restoration force of the unbonded column is higher than in the bonded system because of the distributed PT force along the height of tendons, which causes less energy dissipation.
7 PARAMETRIC STUDY
In the previous section, a bonded PT segmental column was demonstrated to possess higher strength and energy dissipation. Therefore, in the parametric study, the bonded system is investigated. As mentioned before, the stress level in PT strands is not permitted to be higher than 80%. In the quasi-static analysis part, the performance of an emulative conventional monolithic column and three precast bonded samples with 25% (BS25), 40% (BS40), and 70% (BS 70) initial stress levels are compared(BS in the labels, represents the bonded segmental sample).
7.1 Nonlinear-static analysis
The results of the lateral cyclic loading-displacement of the precast segmental and monolithic columns are compared in Fig. 9. As shown in Fig 9(a), the segmental column samples of BS25, BS40 and BS70 are analysed up to 4% drift (150 mm lateral displacement). As the figure indicates, the residual displacement of the segmental columns is negligible due to the restoration capability of the central strands which return the column to its intact position in the unloading stages. Among the segmental columns, the samples with a higher initial stress level show higher stiffness and strength until a 4% drift threshold (i.e., the BS70 sample has the highest strength with 295 kN; while BS40 and BS25 have 263 kN and 228 kN, respectively).
In Fig. 9(b), the monolithic column shows ultimate load of 267 kN at the 3% drift level, which is close to the strength of BS40 segmental column sample. The monolithic column is analysed until 3% drift (108.9 mm lateral displacement) because of the occurrence of a large amount of residual displacement at which point the lateral displacement exceeds a 1% residual drift.
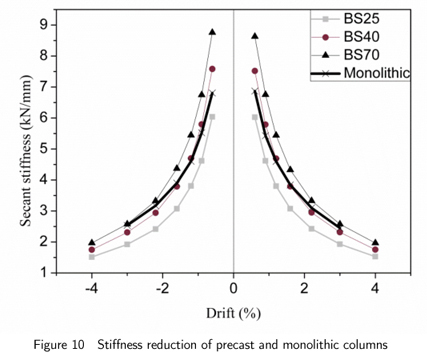
In contrast with the segmental column, the monolithic column exhibits high hysteretic energy dissipation capacity. This is due to high level of induced damage and larger amount of concrete cracks at hinge areas in the monolithic column. The amount of equivalent viscous damping, initial stiffness, stiffness reduction and segment openings in the analysed columns are compared in figures 10-12.
As is shown in Fig. 10, comparing the initial stiffness of the monolithic and post-tensioned segmental columns at 0.6% drift indicates that BS25 column have the lowest amount of stiffness, which is lower than a monolithic column (e.g., 6.0 kN/mm against 6.8 kN/mm stiffness of monolithic column). However, the column with the higher initial stress level (BS70) shows the highest level of initial stiffness (8.9 kN/mm). It can be observed from the figure that the stiffness of the monolithic column is very close to the BS70 sample at 3 % drift, while its initial stiffness is much lower at the start of loading. This shows that the precast PT segmental samples lose their stiffness more than the monolithic sample in larger drifts.
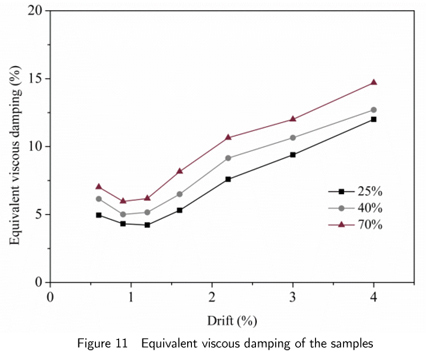
Fig. 11 compares the equivalent viscous damping of BS25, BS40 and BS70 samples up to 4% drift. The equivalent viscous damping has been derived according to Priestley et al. (1996). The results indicate that the energy dissipation of precast PT segmental column samples is low (4 to 14% equivalent viscous damping). In this figure, the samples at a higher initial stress level have slightly higher viscous damping which shows that greater amount of concrete cracks and crushing are induced around the central strands during lateral reverse cyclic loading.
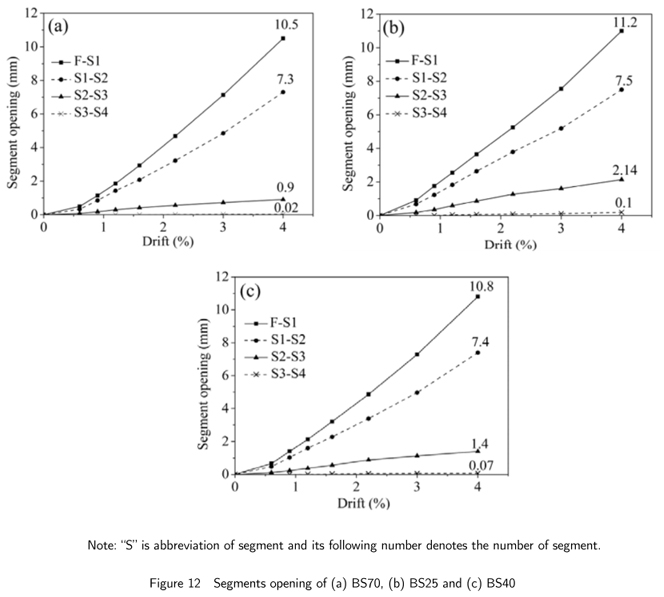
The segment openings of the precast columns at each drift are depicted in Fig. 12. The opening of the first segment is greater than the other segments in all samples. Due to the higher axial PT force in the samples with higher initial stress levels, their segment openings are slightly lower than the columns with lower initial stress. The greatest segment openings occurred in the BS25 column with an 11.2 mm opening at F-S1 (F refers to the footing and S1 represents the first segment).
8 DYNAMIC TIME-HISTORY ANALYSIS
A time-history analysis is imperative in order to evaluate the effect of the prestressing initial stress levels on the dynamic response of precast segmental bridge columns; and compare the performance of precast segmental bridge columns against emulative monolithic conventional bridge columns. Five earthquake records with different peak ground accelerations (shown in Table 4) are utilised to examine the behaviour of the aforementioned samples in low and higher seismicity zones. The earthquake records are obtained from the PEER ground motion database. Fig. 13 shows the applied spectral acceleration of the earthquake records in the present study. In the analyses, a 5% damping ratio has been applied according to the AASHTO (1996) recommendation.
8.1 Results and discussion
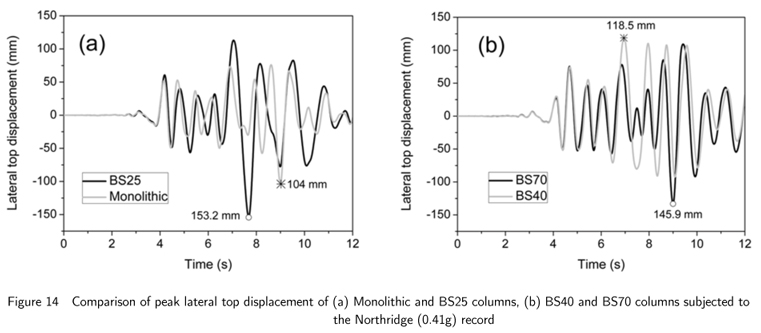
Fig. 14 compares the lateral peak displacements of the self-centring segmental columns at 25%, 40% and 70% prestressing levels and the monolithic column under the Northridge (0.41g) earthquake record. Comparing all column samples, the monolithic column has a lower peak lateral deflection as a consequence of a higher amount of energy dissipation that arises from induced concrete cracks and crushing. The lower lateral peak displacement of the monolithic column, despite of its lower initial stiffness compared to the precast segmental columns with 40% and 70% initial prestressing levels, proves that the longitudinal mild steel ratio is an important parameter to reduce lateral seismic demand. Nonetheless, the large amount of cracks and induced damages in the monolithic column is unavoidable, which challenges the superior performance of the conventional sample against severe earthquake loading.
The time-history analyses in Fig. 14(a) indicate that the BS25 sample has more lateral deflection at the top due to insufficient initial stiffness (lower than the monolithic column). As shown in section 7.1, precast segmental columns have low energy dissipation capacity; and show higher initial stiffness and strength with PT strands at a higher initial stress level. Therefore, the segmental columns with higher initial prestressing force levels are expected to show lower lateral peak displacement against earthquake loading. However, Fig. 14(b) shows that the BS70 sample has a higher peak deflection compared to the BS40 sample. The finding shows that BS70 column loses its initial stiffness more quickly in instances of nonlinear behaviour. In fact, the high level of stiffness and strength of this sample causes excess stress in hinge and jointed areas due to insufficient energy dissipation during severe earthquakes, which leads to concrete crush and damages. Therefore, considerable stiffness loss occurs during seismic loading and exhibits larger lateral peak displacement.
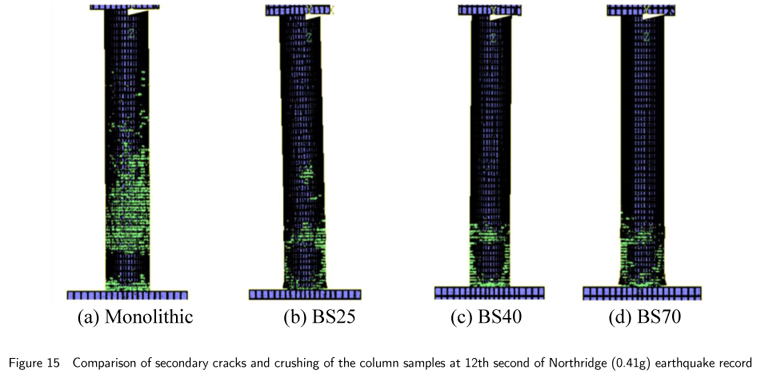
The concrete cracks and crushing of the precast segmental and monolithic columns at 12th second of Northridge record are shown in Fig.15. It can be observed that the cracks and damage induced in precast segmental columns are regional and reparable, while the emulative monolithic columns are highly damaged. The figure also indicates that BS40 columns show less deformation at the joint area of footing-first segment when compared against BS25 and BS70 columns.
The deflections of the precast segmental columns of BS40 and BS70 are compared under the other earthquake records in Fig. 16. Similar results are obtained in Fig. 16(a) and 16(b), where BS70 columns exhibit a larger lateral peak displacement. However, the less-intense earthquake analyses (Figs 16(c) and 16(d)) indicate that BS70 columns show lower peak deflection under the Imperial Valley and Superstition Hills earthquake records. Apparently, the lower deflection of the sample at the high initial stress level (70%) under less-intense earthquakes and lower deflection before reaching peak displacement under severe earthquakes is due to the higher clamping force of the PT strands and consequently higher initial stiffness and strength of the columns.
9 CONCLUSIONS
The force level criteria for post-tensioning is an important factor which should be appropriately selected in various design procedures, such as direct displacement based design, to achieve desirable stiffness, strength, equivalent viscous damping and lateral seismic demand. The present study analytically evaluates and investigates the seismic performance of precast self-centring segmental columns with various post-tensioning force levels. The 3D nonlinear finite element model developed in the present study examines the nonlinear reverse cyclic and lateral dynamic response of hybrid post- tensioned segmental columns. The concurrence of numerical simulation and experimental response implies the accuracy of numerical results. The lateral response of precast segmental columns under seismic loading was compared with emulative conventional columns. Nonlinear reverse cyclic analyses indicate that precast segmental columns show high ductility, relatively low energy dissipation and negligible residual displacement. Conversely, conventional columns exhibit a high energy dissipation capacity with a fat hysteresis loop response and a large amount of residual displacement. Conventional monolithic columns show lower stiffness reduction at 3.0% drift compared to the segmental columns with 25%, 40% and 70% initial stress levels. Among the segmental columns, the sample with the higher initial stress level (70%) exhibited higher stiffness reduction over a 4.0% drift.
Increasing prestressing force levels increasingly affect the initial stiffness and strength of the segmental columns. Moreover, the segmental columns with higher initial stress levels show larger amounts of equivalent viscous damping. However, post-tensioning force levels showed little effect on residual displacement and the joint opening of the precast segmental samples.
Five earthquake records with different peak ground acceleration were applied to examine the performance of self-centring segmental and monolithic columns in low and high seismicity zones. The analyses of less-intense earthquakes showed that the precast segmental columns with a higher initial stress level (70%) have lower peak lateral deflection. However, the analyses of more intense earthquakes indicates that, except for the column with a low initial stress level (25%), the samples with 70%initial stress also indicate relatively high peak lateral displacement, which is undesirable The segmental column with 40% initial stress showed lower lateral seismic demand compared to the other segmental columns. Comparison of concrete cracks and crushing of the segmental columns and emulative monolithic columns subjected to Northridge earthquake record (0.41g) show competence performance of the precast segmental columns with low levels of damage and concrete cracks.
Acknowledgements The authors wish to acknowledge the financial support received from the Fundamental Research Grant Scheme of Malaysia (Grant No. FRGS/TK03/UKM/02/4) in connection with this work.
Received in 29 Apr 2013
In revised form 31 Jul 2013
- AASHTO (1996). Standard specifications for buildings, 16th ED., Washington, D.C.
- American Concrete Institute (ACI). (2002), ACI 318-02, Building code requirements for structural engineering, Famington Hills.
- ANSYS 13, (2012) user's and theory reference Manual.
- Chou, C.C., and Hsu, C-P. (2008), "Hysteretic model development and seismic response of unbonded post-tensioned precast CFT segmental bridge columns", Earthquake Engng Struct. Dyn., 37: 899-921.
- Dawood, H., Elgawady, M. and Hewes, J. (2012), " Behavior of segmental posttensioned bridge piers under lateral loads". J. Bridge Eng. 17 (5), 735-746.
- Desayi, P. and Krishnan, S. (1964), "equation for the stress-strain curve of concrete", J.Am. conc Inst. 61: 345-350.
- Elgawady, M.A., and Dawood, H.M. (2012),"Analysis of segmental piers consisted of concrete filled FRP tubes", Engineering Structures, 38: 142-152.
- Hewes, J.T., and Priestley, M.J.N. (2002), "Seismic design and performance of precast segmental bridge columns" Rep. No. SSRP. 2001, Univ. of California at San Diego.
- ICC (2006), "International building code" International Code Council, Falls Church.
- Kim, T.H., Lee, H. M., Kim, Y.J., and Shin, H. M. (2010),"Performance assessment of precast concrete segmental bridge columns with a shear resistant connecting structure", Enginearing Structures, 32(5), 1292-1303.
- Kwan, W.P., and Billington, S. (2003), "Unbonded posttensioned concrete bridge piers: cyclic loading" J. Bridge Eng. 8 (2), 102-111.
- Marriott, D., Pampanin, S., and Palermo, A. (2008) "Quasi-static and pseudo-dynamic testing of unbonded post-tensioned rocking bridge piers with external replaceable dissipaters", Earthquake Engng Struct. Dyn., 38:331-354.
- Masonry Standards Joint Committee, (2005) "Building code requirements for masonry structures" American Concrete Institute, Farmington Hills, Mich.
- Motaref, S. (2011), "Precast bridge columns with energy dissipating joints", PhD thesis University of Nevada, Reno.
- Ou, Y-C., Chiewanichakorn, M., Aref, A.J., and Lee, G.C. (2007), "Seismic performance of segmental precast unbounded post-tensioned concrete bridge columns" , J. Struct. Eng. , 133 (11), 1636-1674
- Ou, Y-C., Tsai, M.S., Chang, K.C., and Lee, G.C. (2010 a), "Cyclic behavior of precast segmental concrete bridge columns with high performance or conventional steel reinforcing bars as energy dissipation bars" Earthquake Engng Struct. Dyn. 39: 1181-1198.
- Ou, Y-C., Wang, P.H., Tesai, M.S., Chang, K.C., and Lee, G.C. (2010 b), "Large-scale experimental study of precast segmental unbonded posttensioned concrete bridge columns for seismic regions ", J. Struct. Eng. , 136(3), 255-264.
- Palermo, A., Pampanin, S., and Calvi, G.M. (2005), "Concept and development of hybrid solutions for seismic resistant bridge systems ", J. Earthquake Eng. , 9(6), 899-921.
- Palermo, A., Pampanin, S., and Marriot D. (2007), "Design, modelling, and experimental response of seismic resistant bridge piers with posttensioned dissipating connections". J. Struct. Eng.; 133(11): 1648-1661.
- Priestley, M.J.N., Seible, F., and Calvi, G.M. (1996), "Seismic design and retrofit of bridges", Wiley, New York.
- Shim, C.S., Chung, C.H., and Kim, H.H. (2008), "Experimental evaluation of seismic performance of precast segmental bridge piers with a circular solid section". J. Struct. Eng.; 30(12), 3782-3792.
- Stanton, J., Stone, W., and Cheok, G.S. (1998), "A hybrid reinforced precast frame for seismic regions", PCI J. ,42 (2), 20-32.
- Wight, G.D., Kowalsky, M.J., and Ingham, J.M. (2007), "Direct displacement-based seismic design of unbonded post-tensioned Masonry walls ", ACI Struct. j. , 104 (5), 560-569.
- Willam, K.J., and Warnke, E.P. (1974), "Constitutive model for triaxial behaviour of concrete", Proceeding of the international association of bridge and structural engineering conference, Italy, 19 p174.
- Wolanski, A.J. (2004), "Flexural behaviour of reinforced and prestress concrete beam using finite element analysis", Master thesis Marquette University.
Publication Dates
-
Publication in this collection
03 Feb 2014 -
Date of issue
Oct 2014
History
-
Accepted
31 July 2013 -
Received
29 Apr 2013